基于模糊决策的不完整数据分类算法

束建华，李飞凤，方 刚

（1.安徽中医药大学 医药信息工程学院，安徽 合肥 230008；2.淮南联合大学，安徽 淮南 232001）

0 引言

分类作为一个重要数据挖掘方法已经研究多年，已经广泛应用于各个领域［1］.随着中医药信息化的发展，分类也被广泛应用于中医药研究，但疾病信息体现客观不完整和描述疾病的主观不确切，形成了中医病历和中医学信息的不完整性，而不完整的数据的存在总是会降低分类模型的效果.

为了更直观地表达数据不完整的问题，我们假设X1=（1，2，3，4），那么（？，2，3，4）为 25%不完整的数据，（1，？，？，4）为50%不完整的数据.数据缺失的机制分三类［2］：完全随机缺失（missing completely at ran⁃dom，MCAR），缺失值的缺失概率不依赖于数据集中的没有被观察到的值（缺失值），也不依赖于观察到的值（未缺失值）；随机缺失（missing at random，MAR），缺失值的缺失概率是数据集中被观察到的值的函数；不可忽略的缺失（non-ignorable missing），缺失值的缺失概率依赖于数据集中的没有被观察到的值（缺失值）.

目前，已有的基于不完整数据的分类方法主要有：1）忽略不完整数据中的缺损值［3-4］，最简单的方法就是把不完整的数据集中有缺失值的属性删除使其转换成一个完整的数据集，然后针对有完整数据的属性训练建立分类器.但这种策略忽略不完整数据中潜在的有用信息，分类精度降低.如果缺失数据的比例很大，这种调整后数据集上的分类结果更有可能产生误导.2）使用统计学方法（均值法、线性回归法、最大似然法、多值填充法等）填充缺损的值［5-6］，多值填充是在同一填充算法下对缺损值填充多次，得到多个完整的数据集，然后根据某一融合策略计算最后的填充结果，解决了单值填充可能造成的数据偏斜问题，在统计量计算上能得到更高的精确度.3）机器学习方法（朴素贝叶斯、贝叶斯网络、聚类等）填充缺损的值［7-9］.机器学习方法主要是应用已有数据挖掘算法，将填充属性视为类属性，将缺失样本作为测试集完成分类填充.但不完整的数据产生的原因很多，无法确定填充的值是否准确，使用不当会产生严重的数据偏斜.分类问题分为两个阶段：学习阶段和分类阶段.学习阶段是从一组训练数据建立分类模型，而分类阶段把未知数据集（测试数据）分类于预定义的类.大多数已有的算法只关注在学习阶段处理不完整的训练集而对不完整的值出现在分类阶段则无能为力.

决策树分类器可以根据给定的属性值来预测数据的分类，文献［10］给出处理不完整数据的决策树算法的综述.C4.5算法［1］是在学习阶段和分类阶段都对不完整的数据作处理的分类算法，但C4.5处理不完整数据时效率很低.为在学习阶段和分类阶段都很好地处理不完整数据分类问题，本文提出一种新的决策树方法.该方法可以有效地处理不完整数据的分类问题.

AdaBoost 算法核心思想是针对同一个训练集训练不同的弱分类器，然后把这些弱分类器联合构成一个强分类器.众所周知，AdaBoost 算法具有很多优点［11］，能快速收敛到目标，除了迭代次数没有控制属性，能集成多个弱分类器等;但是也存在一些问题，如训练集中含噪音数据，训练样本太少等情况下，Ada⁃Boost算法不能得出稳定的结果.因此，本文在提出新的决策树算法的基础上，使用其决策方法进一步提出一个新的基于模糊决策方法的Boosting 算法，相对于传统的AdaBoost 算法，该方法更多考虑到数据集中的不完整数据，并得到较好的分类效果.

1 C4.5算法

决策树分类算法中最具代表性是著名的由J.Ross Quinlan提出的C4.5算法［1］.C4.5 算法可以同时处理名义数据和数值数据，且可以在学习阶段和分类阶段都处理不完整数据的分类算法，但其在处理不完整数据时效率不高.C4.5的基本思路为：1）对数据源进行预处理（如将连续属性进行离散化处理或将不完整数据转换为完整的数据）形成决策树的训练集；2）如果训练集为空，则生成一个树节点返回；如果训练集中的所有样本均为同一类别，则生成一个叶子节点返回；否则计算每个属性的信息增益率，使用信息增益率来选择分支属性；3）根节点属性的每一个可能的取值对应一个子集UAj，对UAj递归地执行2）过程，直到划分的每个子集中的观测数据在分类属性上取值都相同，生成决策树；4）使用剪枝规则剪枝；5）根据构造的决策树生成分类规则，对测试集进行分类.其中信息增益率的求解如下：

假设A表示数据集中的一个属性；U为每个节点的训练集；UAj是U中属性取值为Aj的子集；|U|是U的样本数；|UAj|是UAj的样本数；类属性的取值为C1，C2，…，Ck-1，Ck；对于属性A其结果表示为：｛OA1，OA2，…，OA（n-1），OAn｝；freq(Ci,U)U中类属性值为Ci的样本数.

首先计算信息熵：

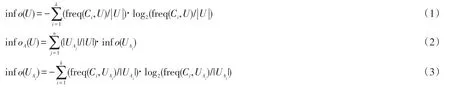
属性A的信息增益Gain（A）使用下式计算：

C4.5算法生成的决策树包含测试节点和叶子节点，测试节点的通过属性信息增益率代替信息增益来选择，属性的信息增益率最大的被选作测试节点，重复该方法直到所有的叶子节点生成.其计算如下式：

C4.5 算法对于连续数据的处理过程为：首先将该属性的所有取值按升序排列，如A1，A2，…，Ai，…，Am，m是该属性取值的个数，对每个属性值Aj，j=1，2，…，m，将样本划分为所有大于该值和所有小于该值的两类，计算这个划分的增益率，然后选择增益率最大的划分.

C4.5算法对于不完整数据的处理过程为：在构造决策树时，对于含缺失值的属性，通常只考虑那些属性值确定的样本，以此来估计该属性的增益率.而在使用决策树时，可以通过计算一个样本中含缺失值的属性不同取值的概率，对一个含缺损值的样本进行分类.但这种方法在处理不完整数据时浪费很多有用的信息，因为计算增益时忽略不完整数据的样本，浪费这个样本的有属性值的数据.例如在表1中，因为属性“temperature”是不完整的数据，样本1 被忽略而计算增益，这浪费属性“outlook”和“windy？”的信息.因此，下文将研究如何使用原始数据的所有有用的信息来生成一个更有效的分类器.

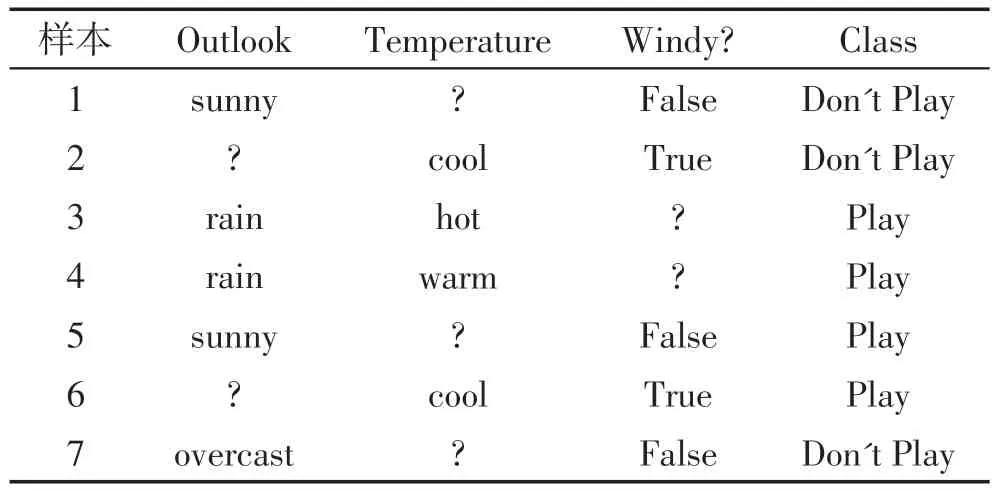
表1 训练集的举例

2 基于不完整数据的新的决策树算法

2.1 新的数据表示方法

为了保持不完整的数据分类问题中所有有用的信息，可以使用拓展的数据表达方式.在表2中提出一种新的数据表示方法：每一行由原来的样本转换得来，每一个样本给出一个权重值，用于表示样本的重要性.这种数据表示看起来简单，但它因为给出每个属性的概率而极大地改进了C4.5.在这种情况下，对所有的训练数据集中给定的属性的不完整数据对应的概率可以计算出来.给定一个特定的属性和类属性值，这个属性的每个可能值的数量除以该类属性值的样本数.然后分配给不完整的数据中缺失值的相应的概率值.例如，属性“outlook”，有3个可能的值：“sunny”、“overcast”、“rainy”，分别有一个“sunny”、一个“overcast”的类属性值“Don’t Play”，共2个“Don’t Play”样本，还有2个“rainy”和1个“sunny”样本的类属性值为“Play”，共3个“Play”样本.样本2的“outlook”属性值是缺失的，其类属性值是“Don’t Play”，所以将其分配为“sunny”、“overcast”各1/2和“rainy”为0；而样本6的“outlook”属性值是缺损的，其类属性值为“Play”，所以分配为“rainy”2/3、“sunny”1/3和“overcast”为0，以此类推，可以将表2填满.

表2 表1的新的数据表示

2.2 新的决策树算法

使用上述新的数据表述方式，定义新的函数用来建立新的决策树.具体的定义和函数描述如下：

每个样本属于某类属性值的权重为：C1(m)，C2(m)，…，Ck(m)，其中Ci(m)表示第m个样本属于类Ci的权重（这里有

每个样本取某一属性中某一属性值的权重为：OA1(m)，OA2(m)，…，OAn(m)，其中OAj(m)表示第m个样本中属性A的取值为Aj的权重（这里有

对于不完整数据：OA′j(mc′i)为OAj(m)中有缺损值的权重，mci为没有不完整数据的样本；mc′i为有不完整数据的样本；Nci为类属性值是Ci的样本数；n（u）为数据集U的样本数；这里有

为数据集U中属性A的取值为j的子集（例如属性 Outlook 有3 个取值sunny，overcast和rain，则数据集U将被分为3个子集）；

weight(m,U)为数据集U中第m个样本的权重；weight(m,UAj)是UAj中第m个样本的权重；freq(Ci,U)为数据集U中类属性值取Ci的样本数；freq(Ci,UAj)数据集UAj中类属性值为Ci的样本数；

|U|为数据集U的样本数，|UAj|为数据集UAj的样本数.

使用上述各定义，熵函数可以定义为

最后，增益率Gain_ratio(A)由公式（10）-（12）得出.

因此，使用上述公式可以计算出各属性的信息增益率，决策树的节点中选择信息增益率最大的属性.为了说明新的决策树的生成过程，我们以表2中的数据为例，选择表2中属性Outlook计算得出表3.

表3 属性Outlook的信息

使用上面的函数，可以计算出：Info（outlook）=0.985 23；InfoA（outlook）=0.381 9；

Split_info（outlook）=1.534 79；Gain_ratio（outlook）=0.393 098.同理可以计算出：

Gain_ratio（Temperature）=0.257 83和Gain_ratio（Windy？）=0.600 544.所以，属性Windy？因信息增益率最大被选择为测试节点.这样生成的决策树如图1所示.

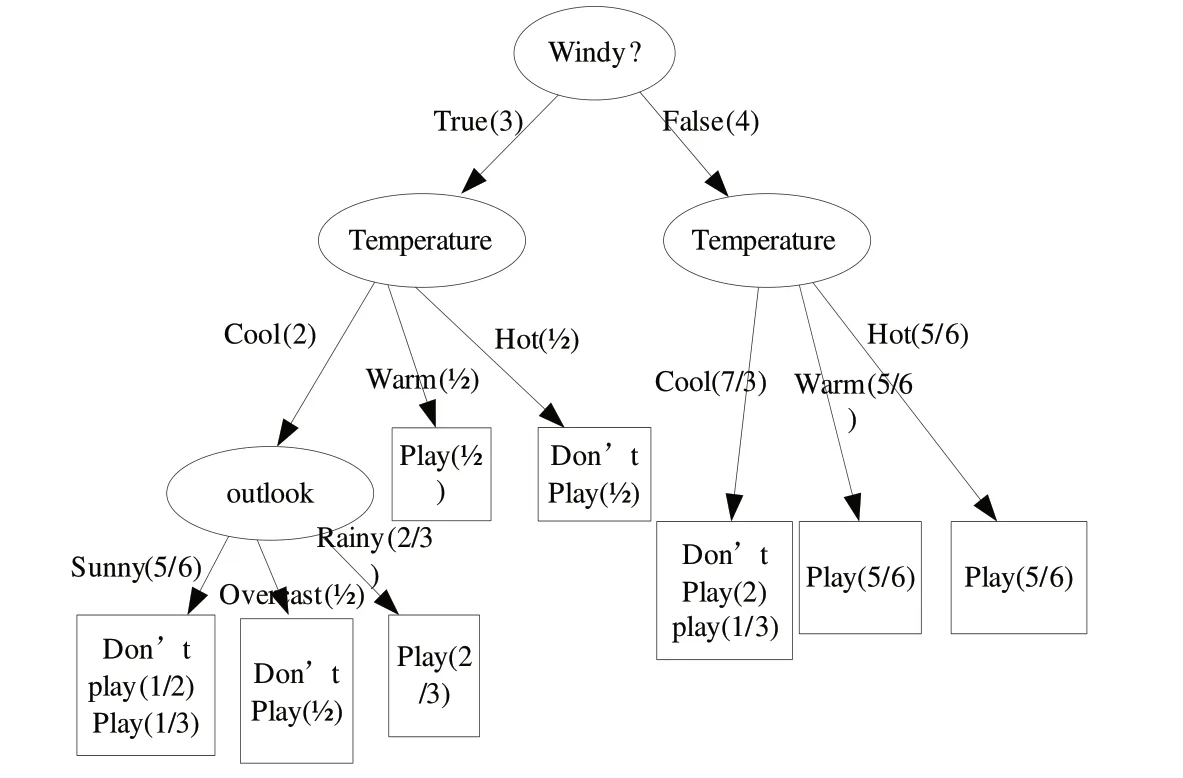
图1 针对表1数据建立的新决策树

3 基于不完整数据的改进的Boosting算法

3.1 改进Boosting算法的基本思路

Boosting算法是每个分类器都对待测样本提供一个分类结果，最终集成这些分类器得出的结果来决定最终的类别，以取得比单个分类器更高的分类精度.与Boosting算法不同的是，AdaBoost算法不需要预先知道弱分类器的分类精度即弱分类器的误差，但最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度.AdaBoost算法开始时，每个样本对应的权重是相同的，即对训练样本训练出一弱分类器，然后给被错误分类的样本比正确分类的样本设置更高的权重，重新生成新的弱分类器，迫使其集中学习其中难以学习的样本.依次类推，经过T次循环，得到T个弱分类器，把这T个弱分类器，使用加权投票的方式得到最终的强分类器.改进的Boosting算法提出在迭代过程中使用基于模糊决策方法代替原来的Ada⁃Boost算法使用的确定性决策方法.在原始算法中，每个分类器的决策就是一个类.例如，如果分类结果是：晴天，雨天，阴天.然后每个分类器的决策只能是晴天或雨天或阴天.然而，实际上，可以给分类器分配概率.例如，明天的天气的预测类的概率是晴天（50%），雨天（30%）和阴（20%）.这样处理后，对于单个分类器的改进可能小，但它可能使集成多个分类器的集成学习算法改进较大，使得集成的分类器可以有更精确的分类结果.但已有的大部分的分类器只能生成确定性决策，因此，本文给出具有模糊决策能力的分类器来提高改进的Boosting算法的分类性能.

在改进的Boosting 算法中，使用基于决策树的分类算法作为弱学习器，更新的规则是减少预测效果好的样本的概率和增加预测效果差的样本的概率.这类Boosting算法的使用可以提供模糊决策的其他分类器，例如MLP（多层神经网络）分类器也可以修改来生成模糊决策.本文使用第三节提出的新的决策树策略.

3.2 算法描述

改进的Boosting算法描述如下：

Step1 初始化训练集中所有n个样本的权重w={wj=1/N|j=1,2,…,N}

Step2 选择T作为迭代次数

Fort=1 toT

Step3 在该数据集上构建新分类器t，返回一个假设ft

Step4 计算分类器t的误差εt：

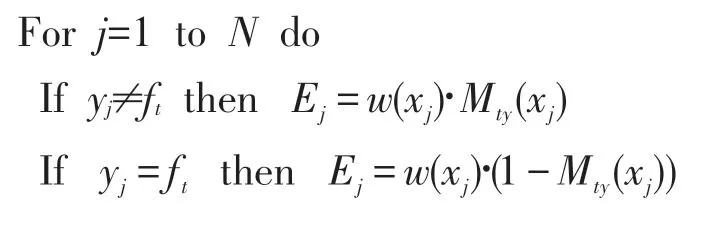
End for

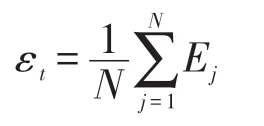
Step5 Ifεt＞1/2，then，并返回到Step3执行.

Step6 重新计算分类器t的权重

Step7 重新设置各个样本的权重

For eachxj

Ifyj≠fi(xj)Thenwi+1(xj)=wi(xj)/Zj·exp(αt)

Ifyj=fi(xj)Thenwi+1(xj)=wi(xj)/Zj·exp(-αt)

End for

End for

3.3 算法分析

改进的Boosting算法的具体分析如下：

（1）用｛(xj,yj)|j=1，2，…，N｝表示有n个训练样本的集合，算法的核心思想是修改权重的分布，一开始时所有的权重相同，但每轮迭代后，不能正确识别的样本的权重增加，使得弱学习器集中学习难以识别的样本.弱学习器的工作是为wi找到一个合适的假设fj，wi是基于分类器的该样本的分类性能分配给每个样本的权重.

（2）选择适当的迭代次数，迭代次数大分类精度可能更高，但花费更多的时间.

（3）本文对每个假设使用第三节提出的新模糊决策，用从样本集中选择的样本生成一个新的分类器，并返回一个假设ft.其中，Mty为ft对每个y∈Y（Y是类属性的值空间）概率.

（4）一个弱假设的好坏取决于它的误差.一个基础分类器fi的重要性依赖于它的误差.误差的计算在Step4 中给出.例如，如果今天是sunny，即yj=sunny，对于ft的模糊决策分别是sunny（50%），rainy（30%）和overcast（20%），则ft=sunny，Mt(sunny)= 0.5，Mt(rainy)=0.3，Mt(overcast)=0.2.计算所有的训练样本后，误差εt用式计算.

（5）如果εt＞1/2，当前的ft被丢弃，选择新的训练子集生成新分类器ft（Step5）.

（6）分类器ft的重要性由参数给出（Step6），参数αt也被用来更新训练样本的权重.

（7）为了说明这一点，使用wi(xj)表示样本(xj,yj)的在第i轮迭代中的权重，权重的更新机制在Step7中给出.其中Zj为标准化因子，用于确保权重的更新机制是增加错误分类样本的权重和减少正确分类样本的权重.

（8）最后的假设fFINAL(x)由T个弱假设通过加权投票得出，其中αt(x)是每个ft的权重，Mjy(x)是ft对于任意的y∈Y的概率.

4 实验结果与分析

为了验证和比较文中提出的新的算法的性能，使用UCI机器学习数据库里的数据集［12］进行以下两组实验.

第一组实验是对于新的决策树算法的验证.

首先选择了Iris数据集，该数据集是模式识别领域最负盛名的数据集之一.该数据集有150个样本，3个类别的实例各50个，每个类别指一种类型的鸢尾属植物，分别为山鸢尾，变色鸢尾和维吉利亚鸢尾.属性的类型包括：花萼的长度、花萼的宽度、花瓣的长度、花瓣的宽度（单位均为cm）.第二个数据集是Pima数据集，数据集有768个样本.分类属性（0或1）分别为500和268个样本属性的类型包括：怀孕的次数、舒张压、年龄等8个属性.

两个数据集都被使用给定的百分率删除部分数据使其成为不完整的数据集.训练数据和测试数据的缺失率分别在表4-7的第一列给出.不完整的数据集生成满足两个要求：每个样本至少有一个属性保留和每个属性知识有一个值保留.实验的结果都是每个数据集10-交叉验证运行10次的平均误差.10-交叉验证是把数据集分为10块，其中9个用作训练集，另1个用作测试集.

第一组实验的第一部分是仅在训练集中使数据不完整，测试集中的数据是完整的，表4和表5是实验的结果.其中“Rule +data”是这样设计的：合并其中的9个块的数据为训练集，再将训练集随机分为两个块，一个块用来生成新的决策树并产生规则，然后规则被加到另一个块中.Rule+data 被用来建立新的决策树来进行分类.从实验结果可以看出，尽管第一个数据块被删除，但由第一个数据块建立的新的决策树产生的规则能作为新增的数据合并到第二个块中，并取得很好的分类效果.

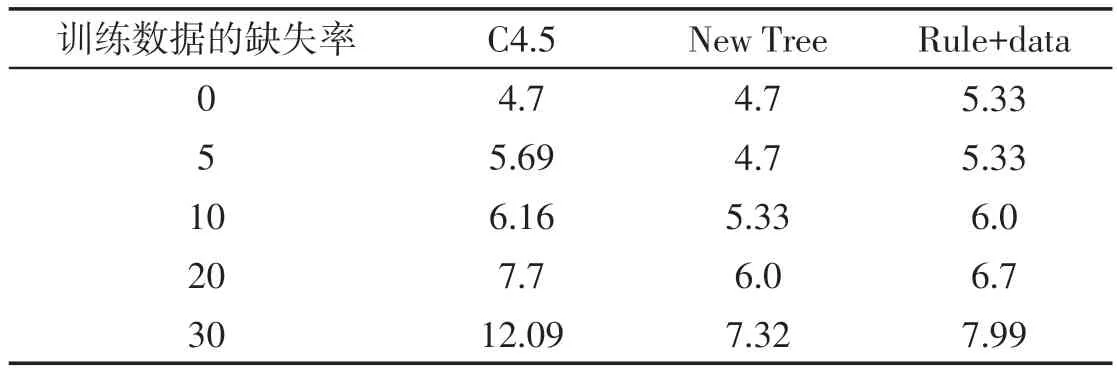
表4 Iris数据的不完整训练集的分类误差 %

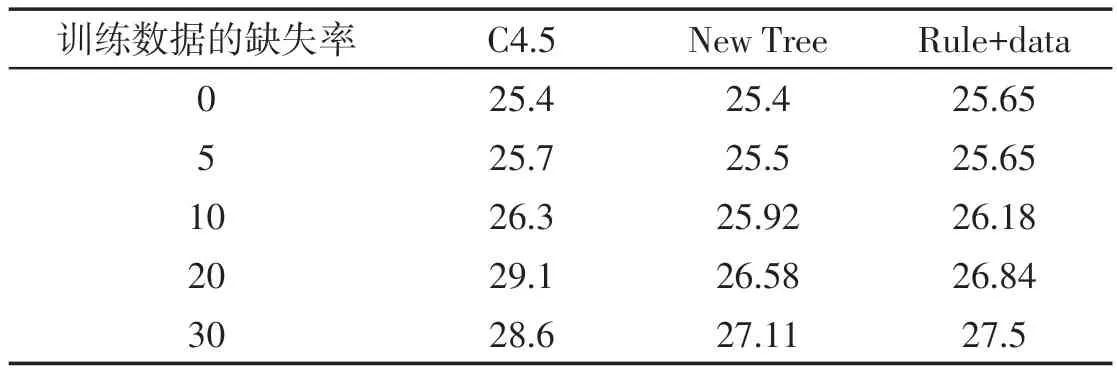
表5 Pima数据的不完整训练集的分类误差 %

第一组实验的第二部分是：不完整数据既在训练集中又在测试集中使用，训练集以10%的缺失率生成决策树，测试集分别以不同的缺失率验证分类的误差.因为除C4.5算法外的分类算法都不能处理学习和分类阶段都使用不完整数据的情况，所以只把新提出的算法和C4.5算法作一比较，表6和表7给出实验的结果.实验结果显示新的决策树算法和Rule+data方法均比C4.5算法优越.

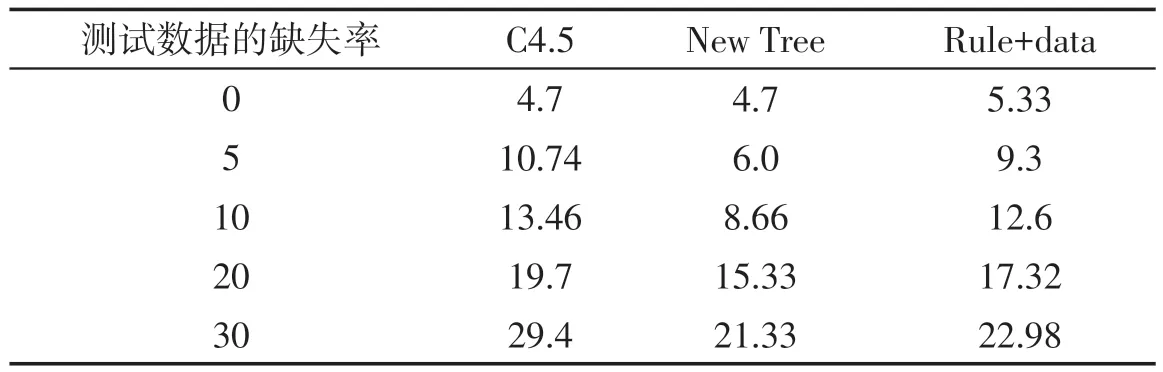
表6 训练集10%缺失率情况下Iris数据的分类误差 %

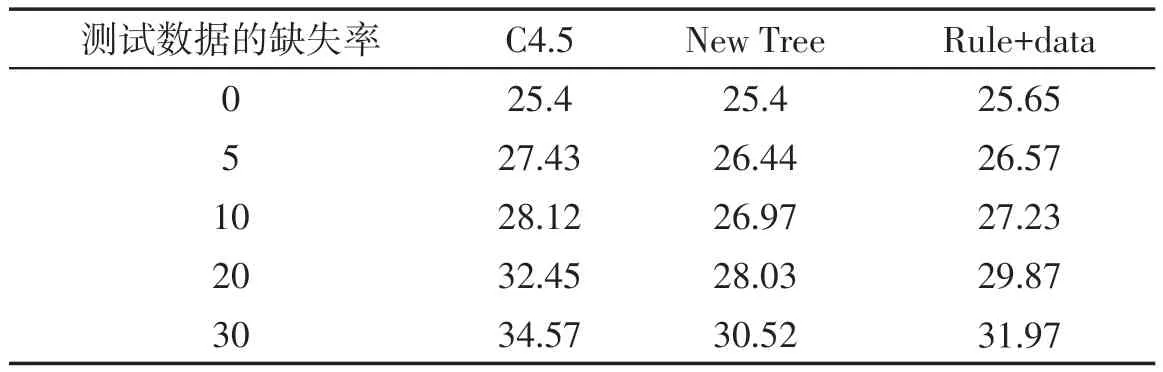
表7 训练集10%缺失率情况下Pima数据的分类误差 %

本组两个实验都有新的决策树算法和Rule+data算法优于C4.5算法.我们注意到Rule+data的情况，一半的原有数据在生成新的决策树后被删除，有其生成的规则加入到另一半数据集中再生成新的决策树，当数据不完整的情况下Rule+data优于C4.5算法，这说明本文提出的新的决策树算法能有效地生成有用的规则，并且不需要存储原始数据而是把规则作为新增数据加入数据集中，这也证明本文提出的新决策树算法是有效且有用的.

第二组实验是对于新的Boosting算法的验证.

本组实验使用UCI机器学习数据库中的Glass和Wine两个数据集.Wine数据集包含178个样本，维数为13，类别数为3.Glass数据集包含214个样本，维数为9，类别数为6.两个数据集都被使用给定的百分率删除部分数据使其成为不完整的数据集.测试数据的数据缺失率在表8的第一列给出，不完整的数据集生成满足2个要求：每个样本至少有一个属性保留和每个属性知识有一个值保留.实验的结果都是每个数据集10次交叉验证运行10次的平均误差.

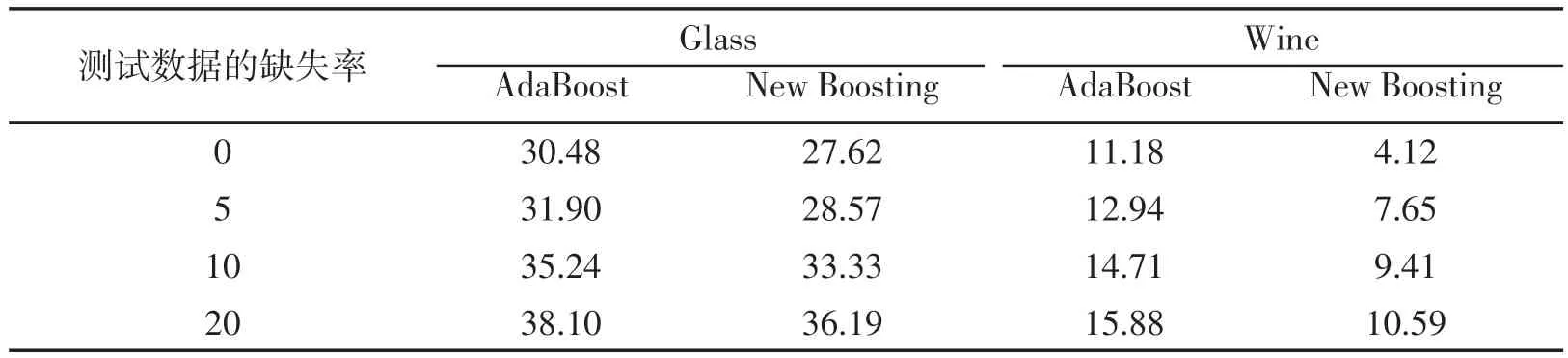
表8 Glass和Wine数据的分类误差 %

5 结束语

本文首先针对不完整数据分类存在的问题，提出一种新的不完整数据的数据表述方式，进一步对C4.5算法进行改进，提出新的决策树算法.实验显示该改进方法的良好性能，且注意到新的决策树生成的规则可以很容易地作为新数据添加到数据集中，并生成一个包含更多信息的另一个新的决策树.实验显示在处理不完整数据时，这个新决策树生成的规则和新数据（Rule+Data）比已有的C4.5算法有更好的分类效果.

其次，在新的决策树算法的基础上，本文还提出一种改进的Boosting 算法用来处理不完整数据的分类问题.在迭代过程中，对每个假设使用模糊决策来选择，最后集成分类结果.该算法也显示其能得出比原AdaBoost算法更好的分类结果.

中医药数据具有关联性、重复性，适合数据挖掘.将数据挖掘应用于中医药领域的研究，是中医药现代化研究的重要组成部分，必将促进中医药的发展.但是中医药数据具有：数据多样性、数据隐私性、数据不完整性、数据冗余性、数据不规范性、数据专业性、数据的时效性和数据挖掘方法的局限性等特征.笔者下一步将研究如何将研究成果应用于处理中医药数据.

［1］杨善林，倪志伟.机器学习与智能决策支持系统［M］.北京：科学出版社，2004.

［2］PIGOTTA T D.A review of methods for missing data［J］.Educational Research and Evaluation，2001，7（4）：353-383.

［3］GRZYMALA-BUSSE J W.Rough set strategies to data with missing attribute values［C］//Workshop Notes，Foundations and New Directions of Data Mining，the 3rd International Conference on Data Mining，Melbourne，Florida，2003.

［4］HATHAWAY R J，BEZDEK J C.Fuzzy c-means clustering of incomplete data［J］.IEEE Transaction on systems，Man and Cybernetics-part B：Cybernetics，2001，31（5）：735-744.

［5］王凤梅，胡丽霞.一种基于近邻规则的缺失数据填补方法［J］.计算机工程，2012，38（21）：53-55.

［6］RUBIN D B.Multiple imputation after 18+ years［J］.Journal of the American Statistical Association，1996，91：473-489.

［7］陈景年，黄厚宽，田凤占，等.一种基于不完整数据的朴素贝叶斯分类器［J］.计算机工程，2006，32（17）：86-88.

［8］杨苹，吕茵，黄锦成.基于模糊聚类的蜂窝小区业务量数据填补算法［J］.计算机工程，2011，37（13）：259-261.

［9］HRUSCHKA Jr E R，HRUSCHKA E R，EBECKEN N F F.Bayesian networks for imputation in classification problems［J］.Journal of Intelligent Information Systems，2007，29（3）：231-252.

［10］VATEEKUL P，SARINNAPAKORN K.Tree-based approach to missing data imputation［C］//Proc of IEEE International Conference on Data Mining Workshops IEEE Press，2009.

［11］YOAV FREUND，ROBERT E S.Experiments with a new boosting algorithm［C］.//Machine Learning：Proceedings of the 15th International Conference，1996.

［12］UCI data summary.http：//www.ics.uci.edu/～mlearn/MLSummary.html.