奇异Liénard方程周期解问题
郑淑媛,鲁世平
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
0 引言
在动力系统理论研究中,具有奇性微分方程周期正解存在性问题一直吸引着很多学者的眼球[1-9],它起源于电子学理论中的电子束Brillouin聚焦问题,该问题可转化为探讨微分方程

周期正解的存在性[1].1972年,文[2]探讨了更广泛的电子束聚焦系统

周期正解的存在性.文[3]研究了一类具有奇性的Liénard微分方程

的周期正解的存在性问题,其中,f:R→R,g:R×(0,∞)→R是L2-Carathéodory函数,且关于t为T-周期函数,并且在x=0 为奇点,即当x→0 时,g(t,x)→∞ 关于t∈R一致成立,令

文[3]得到下面的结论:
定理1假设下面的条件都成立:
(h1)存在常数0<D1<D2,如果x(t)是一个T-周期连续正函数且满足

则D1≤x(τ)≤D2;
(h2)令
(h3)令g(t,x)=g0(x)+g1(t,x),这里g0∈C((0,+∞),R),g1:[0,T]×[0 ,+∞)→R是L2-Caratheodory 函数.g1关于t是可测的,关于x是连续的,对 ∀b>0,∃hb∈L2((0,T),[0 ,+∞))使得

(h4)在x=0 处
(h5)
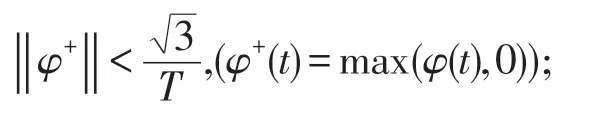
成立,则方程(1)至少存在一个T-周期正解.
文[4]中利用Mawhin重合度拓展定理和一些技巧进一步探讨了一类具有奇性的时滞Liénard方程周期正解的存在性问题,并部分推广了文[3]的结果.有关利用锥上不动点定理和上、下解方法,研究奇异系统周期正解的存在性问题的最新成果可参见文[10-15].
在前人的研究基础上,我们将研究方程

的T-周期正解的存在性,其中,f:R→R是连续的;g0∈C((0,∞),R)在x=0 具有奇性,且g1:[ 0,∞)→R连续;p∈C(R,R),是T-周期的,并满足但是不满足条件(h),
5而(h5)是文[3-4]的关键条件,这就是和前人研究的区别所在.
1 预备定理
令X,Y是两个Banach 空间,L:D(L)⊂X→Y是一个指标为零的Fredholm 算子,则存在投影算子P:X→ kerL,Q:Y→Y,且满足 kerL=ImP,kerQ=ImL.于是

由此可得

是可逆的,设其逆为KP:ImL→D(L)⋂ kerP.设Ω⊂X为有界开集,如果有界,且为X中的紧集,则称非线性算子N在上是L-紧的.
引理 1.1[16]令X,Y是两个 Banach 空间,L:D(L)⊂X→Y是一个指标为零的 Fredholm 算子,且N:→Y在上是L-紧的,其中是X中的有界开集,并且下面所有条件都满足:
(1)对于所有(x,λ)∈[(D(L)⋂∂Ω]×(0,1)有Lx+λNx≠0 ;
(2)对于所有x∈kerL⋂∂Ω有Nx∉ImL;
(3)deg{JQN,Ω⋂ kerL,0}≠0,其中J:ImQ→kerL是同构的.
那么Lx+Nx=0在至少有一个解.
为了应用Mawhin重合度拓展定理,令

线性算子L:D(L⊂X→Y,定义为

非线性算子N:X→Y,定义为

易得

投影算子P:X→kerL,Q:Y→Y分别定义为


由(5)式得对任意的有界开集Ω⊂X,非线性算子N在上是L-紧的.
2 主要结果
定理2.1如果g1∈C((0,+∞),(0,+∞)),g0∈C((0,+∞),(-∞,0)),且下列条件成立
[H1]f∈C((0,∞),R),且存在常数σ>0,使得|f(u)|≥σ,u∈(0,+∞);
[H2]存在常数0<D2<D1,如果x(t)是一个T-周期连续正函数且满足

则存在ξ∈[0,T],使得D2≤x(ξ)≤D1;

[H4]g1(x(t))+g0(x(t))>0,当x∈(0,D2)时,g1(x(t))+g0(x(t))>0,当x∈(D1,+∞)时,其中D1,D2为由[H2]所确定的常数;
那么方程(2)至少有一个T-周期正解.
证明设u(t)为方程

任意T-周期正解,其中L和N分别由(3)和(4)式所定义,即u(t)满足方程

我们往证存在和λ及具体的u(t)无关的三个正常数M0,M1,γ0使得

为了证明(7)式,将方程(6)两端分别在区间[0,T]上积分得

利用假设[H2]可知,存在ξ∈[0,T]和两个正常数D1和D2使得

将(6)两边同时乘以u′(t),并在[0,T]上积分得到


即

利用假设[H1]得

进而由(10)式得

再利用Hölder不等式得

即

由(9)和(11)式得,对任意t∈[ξ,ξ+T],使得

由(6)式得

在[0,T]上其两边积分,可得



因此由(13)式得

因为x(0)=x(T),所以存在τ∈[0,T],使得u′(τ)=0.又对于t∈[τ,τ+T],有

所以可得

在方程(8)两边同乘以u′(t),并在 [ξ,t]⊂[ξ,ξ+T]上积分,可得

其中ξ∈[0,T]由(9)式所确定,结合(11)和(14)式得

因此


如果存在t1∈[ξ,ξ+T],使得u(t1)<ε0,根据(17)式可得

但是(16)与(17)相矛盾.此矛盾说明u(t)>ε0,t∈[ξ,ξ+T].令γ0=ε0,则

由(12),(15)和(19)式可知不等式(7)正确.
定义Ω={x∈X,R1<X(t)<R2,|x′(t)|<R3,∀t∈[0,T]}.
这里 0<R1<min{γ0,D1},R2>max{M0,D2},R3>M2,因此,引理1.1的条件(1)成立.
如果x∈ ∂Ω⋂kerL,那么x(t)=R1或者x(t)=R1,因此有

或者

根据(H4),有

因此,对于所有的x∈kerL⋂∂Ω有Nx∉ImL,所以引理1.1的条件(2)成立.
定义J:ImQ=R→kerL=R,J(u)=u,∀u=R,易得

于是

因此,引理1.1的条件(3)也是满足的.由引理1.1得,方程(2)至少存在一个T-周期正解.
例1考虑下列方程

的2π-周期正解存在性问题,
注1从例1易见,g(x)=g1(x)+g0(x)不满足单边线性增长条件[H5],而[H5]是文[3-4]周期解先验界估计的关键条件.因而,本文的结果是具有新意的,它丰富了文[3-4]相应结果.
[1]丁同仁.关于周期性Brillouin电子束聚焦系统的一个边值问题[J].北京大学学报,1965,1:31-38.
[2]叶彦谦,王现.在电子聚焦理论中的非线性微分方程[J].应用数学学报,1978,1:13-41.
[3]ZHANG M.Periodic solutions of Liénard equations with singular forces of repulsive type[J].J Math Anal Appl,1996,203:254-269.
[4]WANG Z H.Periodic solutions of Liénard equation with a singularity and deviating argument[J].Nonlinear Analysis,2014,16:227-234.
[5]FONDA A,MAnASEVICH R,ZANOLIN F.Subharmonic solutions for some second order differential equations with singu⁃larities[J].SIAM J Math Anal,1993,24:1294-1311.
[6]TORRES P J.Existence of one-signed periodic solutions of some second order differential equations via a Krasnoselskii fixed point theorem[J].J Differential Equations,2003,190:643-662.
[7]HABERTS P,SANCHEZ L.Periodic solutions of some Liénard equations with singularities[J].Proc Amer Math Soc,1990,109:1035-1044.
[8]JIANG D,CHU J,ZHANG M.Multiplicity of positive periodic solutions to superlinear repulsive singular equations[J].J Differential Equations,2005,211:282-302.
[9]LAZER A C,SOLIMINI S.On periodic solutions of nonlinear differential equations with singularities[J].Proc Amer Math Soc,1987,88:109-114.
[10]TORRES P J.Weak singularities may help periodic solutions to exist[J].J Differential Equations,2007,232:277-284.
[11]FRANCO D,WEBB J K L.Collisionless orbits of singular and nonsingular dynamical systems[J].Discrete Contin Dyn Syst,2006,15:747-757.
[12]BONHEURE D,FABRY C,SMETS D.Periodic solutions of forced isochronous oscillators at resonance[J].Discrete Con⁃tin Dyn Syst,2002,8(4):907-930.
[13]BONHEURE D,DE COSTER C.Forced singular oscillators and the method of upper and lower solutions[J].Topol Meth⁃ods Nonlinear Anal,2003,22:297-317.
[14]ROBERT H,TORRESB P J.On periodic solutions of second-order differential equations with attractive-repulsive singu⁃larities[J].Journal of Differential Equations,2007,239:196-212.
[15]CHU Jifeng,TORRES P J,ZHANG Meirong.Periodic solutions of second order nonautonomous singular dynamical sys⁃tems[J].J Differential Equations,2007,239:196-212.
[16]GAINES R E,MAWHIN J L.Lecture notes in mathematics[M].Berlin:Springer-Verlag,1977.

