高中数学函数对称性的探究
吉林省临江市第一中学 王 杰
新课标高中数学教材上就函数的性质着重讲解了单调性、奇偶性、周期性,但在考试测验甚至高考中不乏对函数对称性、连续性、凹凸性的考查。尤其是对称性,因为教材上对它有零散的介绍,例如二次函数的对称轴,反比例函数的对称性,三角函数的对称性,因而考查的频率一直比较高。以笔者的经验看,这方面一直是教学的难点,尤其是抽象函数的对称性判断,对称关系还充分体现了数学之美。本文拟通过函数自身的对称性和不同函数之间的对称性这两个方面来探讨函数与对称有关的性质。
一、函数自身的对称性探究
定理1:函数 y = f (x)的图像关于点A (a ,b)对称的充要条件是f (x)+ f (2a-x) = 2b.
证明:(必要性)设点P(x,y)是y=f(x)图像上任一点,∵点P(x,y)关于点A (a,b)的对称点P‘(2a-x,2b-y)也在y=f(x)图像上,∴2b-y=f(2a-x)
即y+ f(2a-x)=2b故f(x)+f(2a-x)=2b,必要性得证。
(充分性)设点P(x0,y0)是y = f(x)图像上任一点,则y0= f (x0)
∵ f (x)+ f(2a-x) =2
∴f (x0) + f (2a-x0) =2b,即2b-y0= f (2a-x0)。
故点P‘(2a-x0,2b-y0)也在y=f(x) 图像上,而点P与点P‘关于点A(a,b)对称,充分性得征。
推论:函数 y= f (x)的图像关于原点O对称的充要条件是f(x)+f(-x)= 0
定理2:函数 y= f(x)的图像关于直线x=a对称的充要条件是f(a+x) = f(a-x) 即f(x)=f(2a-x) (证明留给读者)。
推论:函数 y= f(x)的图像关于y轴对称的充要条件是f(x)= f(-x)
定理3:①若函数y = f (x) 图像同时关于点A (a ,c)和点B (b ,c)成中心对称(a≠b),则y = f (x)是周期函数,且2|a-b|是其一个周期。②若函数y=f(x) 图像同时关于直线x=a和直线x=b成轴对称 (a≠b),则y =f (x)是周期函数,且2| a-b|是其一个周期。
③若函数y= f(x)图像既关于点A(a ,c) 成中心对称又关于直线x =b成轴对称(a≠b),则y=f (x)是周期函数,且4|a-b|是其一个周期。
①②的证明留给读者,以下给出③的证明:
∵函数y = f (x)图像既关于点A(a ,c) 成中心对称,
∴f (x) + f (2a-x) =2c,用2b-x代x得:
f (2b-x)+f[2a-(2b-x)]=2c………………(*)
又∵函数y= f(x)图像直线x =b成轴对称,
∴ f(2b-x)= f(x)代入(*)得:
f(x)=2 c-f[2(a-b)+x]…………(**),用2(a-b)-x代x得
f[2(a-b)+x]=2c-f [4(a-b) +x]代入(**)得:
f(x)= f[4(a-b)+x],故y= f(x)是周期函数,且4|a-b|是其一个周期。
二、不同函数对称性的探究
定理4:函数y= f(x)与y= 2b-f(2a-x)的图像关于点A (a ,b)成中心对称。
定理5:①函数y=f(x)与y=f(2a-x)的图像关于直线x=a成轴对称。②函数y=f(x)与a-x= f (ay)的图像关于直线x+y=a成轴对称。③函数y=f(x)与x-a=f(y+a)的图像关于直线x-y=a成轴对称。
定理4与定理5中的①②证明留给读者,现证定理5中的③,设点P(x0,y0)是y= f(x)图像上任一点,则y0=f (x0)。记点P(x,y)关于直线x-y = a的轴对称点为P‘(x1,y1),则x1=a+y0, y1= x0-a ,∴x0= a + y1, y0= x1-a 代入y0= f (x0)之中得x1-a= f(a + y1) ∴点P‘(x1,y1)在函数x-a= f(y + a)的图像上。
同理可证:函数x-a= f(y+a)的图像上任一点关于直线x-y=a的轴对称点也在函数y=f(x)的图像上。故定理5中的③成立。
推论:函数y= f(x)的图像与x=f(y)的图像关于直线x=y成轴对称。
三、三角函数图像的对称性列表
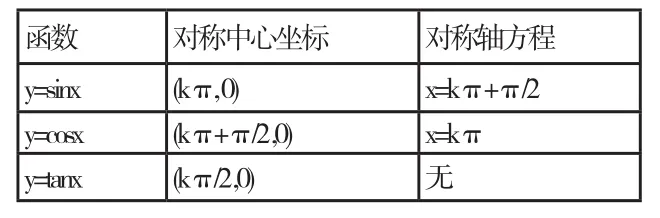
注:①上表中k∈Z;②y=tan x的所有对称中心坐标应该是(kπ/2,0),而在岑申、王而冶主编的浙江教育出版社出版的21世纪高中数学精编第一册(下)及陈兆镇主编的广西师大出版社出版的高一数学新教案(修订版)中都认为y=tanx的所有对称中心坐标是(kπ,0),这明显是错的。

