基于Mumford-Shah模型的图像处理
李浩,毕翔,豆泽阳
(中国传媒大学 理学院,北京 100024)
基于Mumford-Shah模型的图像处理
李浩,毕翔,豆泽阳
(中国传媒大学 理学院,北京 100024)
讲述了偏微分方程的基础数学理论,诸如:梯度、散度、变分定理、欧拉-拉格朗日方程等知识;然后重点介绍了Mumford-Shah模型及Ambrosio-Tortorelli的近似求解,最后进行了数值试验并展开分析。
数字图像;偏微分方程方法;变分定理;Mumford-Shah模型
1 数字图像
我们处在图像的世界里,图像是客观事物在人眼中的表现,可以帮助人们理解外部事物的变化。由于图像的重要性日益凸显,数字图像处理应运而生。数字图像处理是指通过计算机对图像的处理和加工,使人们得到重要的信息。在最初,图像处理主要在天文、军事、医学等实际方面应用,这也是数字图像处理发展的源头。随着社会的发展,尤其是人们迈入了信息社会,图像的产生来源成爆炸式增长,数字图像处理更得到了飞速的发展。随处可见的智能手机、平板电脑、数码相机等设备都应用了数字图像处理技术。随着图像处理和其他科学研究的不断发展并由此产生出更加吸引人的领域,如人工智能、机器视觉、机器学习等。
数字图像处理主要包括图像去噪、图像增强、图像压缩、图像恢复、图像分割等,这些图像处理技术又称为低层的图像处理技术。但正是这些低层的处理技术制约着计算机视觉等领域的发展,所以对于低层处理技术的研究得到国际上的广泛关注。图像处理发展至今已经产生了很多的分支,主要为三种:随机过程建模、小波理论、偏微分方程方法(简称PDE方法)[1]。近年来,PDE方法处理图像问题得到了飞速的发展,诸如熟知的P-M模型、ROF模型、C-V模型以及本文讨论的Mumford-Shah模型等。PDE作为一门基础的数学学科,理论较为复杂,对于非数学背景的研究人员来说理解较为困难。但不可否认的是,PDE处理图像问题的一个优势在于:有严谨的数学理论做基础。我们可以把具体的图像处理问题抽象为数学模型,用稳定的、成熟的数值计算方法求解。在讲述模型之前,先了解一些PDE处理图像问题的数学理论基础。
2 数学理论基础
PDE图像处理涉及到的知识有平面微分几何、变分学、数学物理方程、计算方法等,由于变分学、偏微分方程数值解等知识都可以分别的当做独立的数学知识,所以在这里都不会进行详尽的讨论,重点放在了之后的图像处理模型上面,这里只是简要阐述这些知识。
2.1 梯度与散度

原图像F 梯度分量Fx 梯度分量Fy 梯度模|▽F|图1 原图像及其梯度分量和梯度模图像
2.2 变分问题
对泛函求极值的问题称为变分问题,得到的解即为变分问题的解,也称为极值点,这里就与一般空间上的函数求极值问题所对应上了,所不同的就是求解方法问题,这也是变分学所研究的内容,下面引入变分定理。
定理1变分定理
有泛函:
F(u)=∫Cφ(x,y,u(x,y),ux(x,y),uy(x,y))dC
(1)
它的极值必满足以下的方程:
(2)
称为泛函F(u)的欧拉-拉格朗日方程。

2.3 梯度下降法求解变分问题
直接求解欧拉-拉格朗日方程十分困难,我们求得的解很多时候也不是解析解,最常用的方法就是梯度下降迭代法。梯度下降法的基本原则简要说是:某函数从初始位置u0出发,沿着其负梯度方向进行搜索,最终达到函数的局部极小值点。上述变分定理中,(2)式可以看做是(1)式的求梯度,故由梯度下降法,求解欧拉-拉格朗日方程极值点的方法可以写为:
(3)

3 Mumford-Shah模型及其求解
3.1Mumford-Shah模型
在图像分割的任务中,我们要求分割出图像中的同性质的区域,划分出图像的组成部分,提取信息。而图像恢复中,我们要求得光滑图像,更好的复原图像的原本面貌。在1985,Mumford-Shah提出了以他们名字命名的模型Mumford-Shah模型[3],即M-S模型,此模型能同时完成图像分割和图像恢复的任务。
M-S模型是一种能量极小化泛函,函数u:→R,是有界开区域,不连续边界集K⊂。
minF(u,K)=∫(u-g)2dx+p∫|▽u|2dx+τ∮Kds
(4)
F(u,K)中u表示要求得的图像,K表示求得的边界集,g是初始的图像,一般为带噪声的图像,p与τ为正整数参数。在M-S极小化泛函中,第一积分项为保真项,这使得求得的新图像与初始图像最接近;第二积分项使得解到的新图像在不连续的集合外尽可能的光滑;第三积分项使得不连续的边界集合的长度最小。在这三个积分项的约束下,就可以得到原图像的光滑图像和分割图像。
3.2 Ambrosio-Tortorelli近似模型
在(4)式中的第三积分项是不连续的点集K的Hausdroff测度的几何项,而K的离散化非常复杂,由于该项的存在,使得M-S模型求解非常麻烦[1]。一般的求解方法是在sobloev空间寻找正则泛函序列Fδ来逼近F(u,K),这里讨论的就是Ambrosio-Tortorelli提出的椭圆逼近方法。所谓的椭圆逼近方法就是不去直接离散化M-S模型,而是通过求取它的椭圆逼近来近似求解M-S模型的解。Ambrosio-Tortorelli提出的方法为[4]:
minF(u,v)=∫(u-g)2dx+p∫|▽u|2dx+τ∫(ε|▽
(5)
下面开始对(5)式进行求解,我们需要用到欧拉-拉格朗日方程式(2),得:
即:
(8)
在上式中,为了使梯度下降格式更加稳定我们分别加入了系数θu、θv。现在需要用有限差分方法来离散求解(8)式,并应用的是高斯-赛德尔迭代[5]。我们规定区域是一个(0,m)×(0,n)的矩形区域,让xi=ih,yj=jh是区域里步长为h的离散格式。
规定:
ui,j→u(xi,yj),vi,j→v(xi,yj),gi,j→g(xi,yj)

△u→(ui+1,j+ui-1,j+ui,j+1+ui,j-1)/(h2);
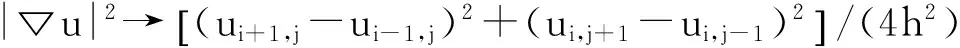
对于vi,j也是同样的离散方法。
(8)式可变为:


在开始迭代之前,ui,j是给定的初始图像gi,j,vi,j中的值全部为1。
3.3 数值试验
通过调节ρ,τ,ε这些系数,可以达到对大多数图像的分割和去噪,SNR曲线和分割效果如下所示,SNR曲线中第一步是初始图像的信噪比,第二步是第一次迭代的信噪比,如此类推。
下面令ρ=0.008,τ=1,ε=0.015,分别对lena图像和man图像处理。

初始图像 去噪图像 嗓声图像 分割图像图2 lena图像处理结果

图3 去噪的lena图像snr曲线

初始图像 去噪图像 嗓声图像 分割图像图4 man图像处理结果

图5 去噪的man图像snr曲线
图2和图4表明:对不同的图像进行试验得到的结果,汇总了分割效果图和去噪效果图,图3和图4是关于这两幅图像的去噪的SNR曲线示意图,横轴表示了迭代次数,纵轴表示了SNR大小。由以上4幅图像可以看出,在上述的系数确定的情况下,迭代次数在6次之后,图像的结构趋于平稳,得到了这两个解:分割图像和去噪图像。同样也试了一些其他的灰度图像,如:pepper图像和grid图像,图6、图7为实验结果。

初始图像 去噪图像 嗓声图像 分割图像图6 pepper图像处理结果

初始图像 去噪图像 嗓声图像 分割图像图7 grid图像处理结果
4 总结
本文在对数学基础理论讨论的基础上,对PDE图像处理的模型Mumford-Shah泛函进行阐述,让读者有了大致的了解,并知道了在M-S模型中不连续边界点集在离散化方面十分困难,所以接着讨论了Ambrosio-Tortorelli提出用椭圆型方程近似代替M-S模型的方法,利用欧拉-朗格朗日方程和梯度下降流来实现方程的求解,并用有限差分法来离散,最后用Matlab进行了数值实验。由以上实验可见,本文讨论的方法可以说是双变量系统,在变分引理的条件下进行求解,得到了两个“最优解”,即:去噪图像和分割图像,在这个情况下,调节各个系数的取值可以得到更优的结果。由此可见,PDE图像处理的方法是十分清晰的,理论的证明也是十分的严谨,在实现上也比较简单,并且对许多的图像都有很好的处理效果。
[1]朱才志.基于偏微分方程的数字图象处理的研究[D].合肥:中国科学技术大学论文集,2007.
[2]Alfonso Vitti.The Mumford-Shah variational model for image segmentation:An overview of the theory,implementation and use[J].Journal of Photogrammetry and Remote Sensing(ISPRS),2012,69(3):50-64.
[3]Mumford D,Shah J.Optimal approximation by piecewise smooth functions and associated variational problem[J].Comm Pure Appl Math,1989,42(5):577-685.
[4]Ambrosio L,Tortorelli V.Approximation of functionals depending on jumps by elliptic functionals via C-convergence[J].Communications on Pure and Applied Mathematics,1990,43 (8):999-1036.
[5]Antonin Chambollet.Image segmentation by variational methods:mumford and shah functional and the discrete approximations[J].Society for Industrial and Applied Mathematics,1995,55(3):827-863.
(责任编辑:王谦)
The Image Processing Based on Mumford-Shah Model
LI Hao,BI Xiang,DOU Ze-yang
(School of Science,Communication University of China,Beijing 100024,China)
this paper introduces some mathematic theories,such as gradient,divergence,variational theorem,the Euler-Lagrange equation and so on.Then we discuss the Mumford-Shah model and its approximation,named Ambrosio-Tortorelli model.At last we implement the model and analysis the result.
digital image;partial differential equation;variational theorem;Mumford-Shah model
2015-04-12
李浩(1990-),男(汉族),山东济宁人,中国传媒大学硕士研究生.E-mail:imagelihao@163.com
O24
A
1673-4793(2015)06-0056-07

