火炮高平机复杂系统参数优化

王妍智，顾克秋

(南京理工大学 机械工程学院， 江苏 南京 210094)

火炮高平机复杂系统参数优化

王妍智，顾克秋

(南京理工大学 机械工程学院， 江苏 南京 210094)

为解决超轻型大口径火炮手轮力较大的问题，利用参数优化设计方法，进行高平机复杂系统寻优设计。建立高平机结构、位置、特性等参数的数学关系，通过Matlab编程计算全射程范围内手轮力。建立以手轮力最大值最小为优化目标的单目标优化模型，采用多岛遗传算法与胡克基夫组合优化算法，通过多学科优化软件iSight集成Matlab进行寻优，得到使手轮力最大值最小时的参数值。优化结果对超轻型火炮高平机设计具有指导意义，使其符合实际可操作性，达到了改进设计目标；该优化模型的建立为传动系统的优化问题提供了一种新思路。

火炮； 高平机； 优化设计

0 引言

为适应现代战争所要求的机动性，作为地面部队主要压制火力的火炮轻量化设计成为火炮现代设计中的重要课题。高平机是火炮轻量化设计的产物，是将高低机和平衡机结合在一起，具有调节高低射角和减小手轮力的双重效果的新型结构。其结构紧凑、操作方便的特点，不仅使全炮质量大大降低，而且能够保证良好的机动性能。传统火炮高平机设计方法过于依赖工程人员的经验，且很难得到性能最优的结构，所以基于先进设计理论与方法的高平机参数优化研究具有重大意义[1]。

为了更加充分地挖掘高低系统的优良性能，提高传动系统效率，有必要进一步对整个高低系统进行优化。国内已经有学者对高平机进行了初步优化，但是模型过于简化，不符合实际。对于文中分析的对象，螺杆气压式高平机来说，要提高手轮力以及系统整体的效率，不能局限于高平机部件。高平机部件属于火炮高低系统的一部分，要得到手轮力的最优力学性能，就必须考虑高平机部件在高低系统中的耦合关系，将从驱动装置手轮到执行部件高平机之间的所有传动环节，包括由花键副、万向节、螺杆螺母副等组成的整个传动链视为优化对象。文中旨在找到最优性能下的各参数的相对最优解。针对简单结构或零件传动刚度、效率等传统问题，前人虽进行过定性分析和研究，但却没有很好的应用到复杂机械系统传动的优化分析中，目前国内对机械传动的优化仅局限于齿轮、丝杠等局部零部件的优化。在前人的基础上进行深层次的探究，将整个火炮高低系统作为一个复杂的机械系统详细分析并进行建模寻优计算，这对目前正在研究的新型轻量化牵引火炮具有重大意义。作为新的分析手段在传统问题上的应用，这种新的探索不仅代表了现代机械设计的趋势，而且对实际生产设计具有很好的指导作用[2-4]。

1 高平机系统结构及工作原理

文中研究的是螺杆气压式高平机，即高低机功能由螺杆螺母实现，平衡机功能由密闭腔高压气体实现，并通过弹簧在大射角时补偿。左右高平机对称布置，通过传动杆相连，同步运动。火炮被赋予某个射角后，起落部分产生的重力矩被平衡力矩抵消一部分，剩余的不平衡力矩由高低机承受并实现自锁[5]。

当打高火炮射角时，转动手轮，使输入转矩通过锥齿轮以及万向花键联轴节传递给高平机左侧齿轮箱，通过传动箱及传动杆带动左右两侧螺杆同步转动，使得螺母相对螺杆向上运动，带动外筒相对内筒向上滑动，从而带动摇架射角增大，起到高低机的作用。外筒和内筒间装有高压气体和密封液体，当外筒相对内筒向上滑动时，由于空间体积的增大使气体压力按多方规律下降，产生较小的平衡力，从而可以克服较小的起落部分力矩，完成平衡机的功能。

当打低火炮射角时，原理与打高火炮射角时相同，通过螺母相对螺杆向下运动带动摇架射角减小；通过气体压力上升，产生较大的平衡力克服较大的起落部分力矩。高平机传动机构原理图如图1。

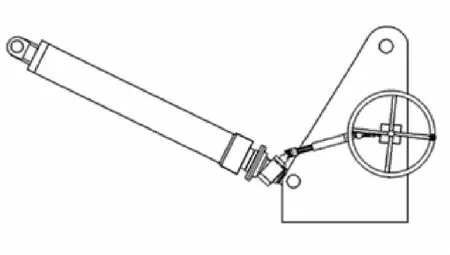
图1 高平机传动机构原理图

手轮传动箱固定于上架，经高低传动机构，使摇架绕上架耳轴进行转动，此传动链为一闭链传动，且左右高平机并联对称布置，同步运动，故在分析机构位置时可将高平机传动系统视为图2所示的平面机构。

图2 机构传动简化示意图

由图2可知，以射角为零度时的位置作为初始坐标位置，A点代表上架耳轴，B点为高平机上铰轴；杆AB代表摇架，通过A点与上架铰接，通过B点与左右高平机铰接。G点为高平机下铰轴与上架的链接位置，BG代表高平机部件，其中移动滑块代表高平机螺筒与螺杆的移动副链接关系。F点为左右高平机间传动杆位置，E点为前万向节联轴器中心位置，FE为带动高平机螺杆传动的输入齿轮轴，F点与两齿轮轴相交位置重合，两轴夹角为要优化的结构安装尺寸。D点为后万向节联轴器中心位置，将E、D点简化为平面上的转动副，E、D之间通过移动副链接，代表空间上的花键结构。C点为火炮上架上的点，将上架视为地面，则A、D两点同时固接于地面，其中C点为手轮轴与计算平面的垂直交点；CD为手轮带动的齿轮轴。

图2为由旋转副和移动副组成的简单平面机构，自由度为一，可将其视为两个平面四杆机构的组合，即曲柄滑块机构ABHG和曲柄滑块机构GEID，在对其进行运动学分析时可使用矢量三角形的方法。

2 手轮力相关因素运动学分析

万向节两端的齿轮轴装配角度可调，直接影响到不同高低射角下前后万向节夹角，而在夹角过大时会极大的降低传动效率。将通过空间传动机构简化为平面连杆传动机构的方法计算万向节传动夹角的表达式，进而计算出万向节花键轴的传动效率，而分析平面传动机构位置关系的同时也可以精确计算出变结构重力矩力臂的长度，修正前人将其视为简单正弦函数所带来的误差。

a) 万向节夹角计算

建立整体坐标系，利用矢量环建立各点和杆件位置之间的关系。建立如图3所示坐标系o-xy，AB与水平线的夹角，范围为-3°至65°，以左水平线作为AB杆角度的参考位置，顺时针为正，逆时针为负。坐标原点设定在下支点G处。

将AB杆的转动角作为输入 ，转角范围是-3°至65°，FE与ED间的所夹锐角为α，ED与水平线的夹角为β，可用θ来表示。为方便使用矢量三角形法分析，将图2演变成图3所示机构。

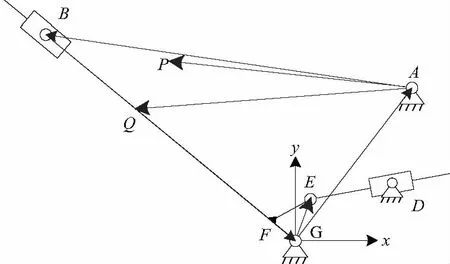
图3 机构运动分析矢量示意图

建立如图3所示坐标系o-xy，易得A、B、C、D、E、F、G各点初始坐标。

B的动态坐标表达式通过矢量环来确定：

GA+AB+BG=0

(1)

(2)

(3)

可以得到下式：

(4)

则B点的坐标值：

(5)

GB的单位方向矢量为：

(6)

则GF可表示为：

(7)

为方便后续的速度、加速度、力等的分析，采用变换矩阵的方式求解FE的矢量。

在G点建立局部坐标系O-xy，该坐标系与连杆GB固结的，坐标系O-xy到o-xy的旋转矩阵为：

(8)

GB与GE的夹角固定，通过余弦公式计可以算得GB、GE、BE的杆长。GB与GE的夹角大小为φ，GE在坐标系O-xy中可表示为GE′矢量：

(9)

GE=T·GE′

(10)

ED=GD-GE

(11)

EF=GF-GE

(12)

可求得后万向节夹角为：

(13)

可求得前万向节夹角为：

(14)

b) 万向节效率计算

以往在理论计算手轮力时，将传动的效率估算为一个常数值，但是对于文中研究的火炮的传动结构来说，这样的分析方法会在不同射角时产生较大的偏差，所以给出打高低射角过程中效率的计算公式，即效率是随射角变化而变化的变量。

根据经验对前人用过的万向节效率公式进行修正，传动系统中有锥齿轮副m个，滚动轴承n个，则单个万向节效率计算公式为：

(15)

(16)

η=fαfβη花键η锥mη滚n

(17)

c) 变结构质心位置修正

起落部分包括上部架体和与高平机外筒固接的部分，两者的相对位置在火炮改变高低射角时随之改变，前人的分析方法是直接将其在零度射角的质心与转动中心——耳轴的距离看做旋转半径，继而计算重力矩。但这样的处理方法在较大射角时会带来较大的误差，即起落部分的质心位置不是随射角简单变化的线性函数，这就需要对组成高低系统两部分分别计算其相对于耳轴的力臂，再通过加权平均的方法算出瞬时的质心。

设上部架体质心位置为动点N，高平机外筒质心位置为动点M，则两点处的质量相对于耳轴A重力矩的力臂应为矢量AN、AM的水平分量的绝对值。

先求出矢量GM

(18)

通过矢量三角形GAM可得到AM矢量：

AM=GM-GA

(19)

则，点M与点A的水平距离为向量AM的水平分量：

(20)

在初始位置时AN连线与水平线的夹角为：

(21)

可得任意射角时N与点A的水平距离为：

(22)

由上可计算重力矩力臂为：

(23)

3 手轮力分析计算

高平机受力分析示意图如图4所示，图中O为耳轴中心，A为高平机与摇架相连接的上支点，B为高平机与上架相连接的下支点，β为OA、OB的夹角，G为起落部分的质心，lq为耳轴O点与起落部分质心G点之间的距离，φ为起落部分的高低射角，γ为OG与水平线的夹角，h为耳轴O点到AB直线间的距离，Fp为高平机产生的平衡抗力，l为上下支点AB间距离，g为重力加速度，r1为耳轴与上支点距离，r2为耳轴与下支点距离。下文所示符号的脚注中，0表示高低射角为0时的状态，j表示高低射角为j时的状态，-3≤j≤65,j为整数。

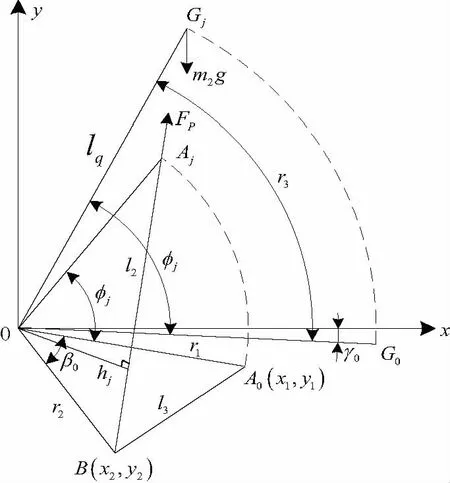
图4 高平机受力分析

a) 几何位置

(24)

(25)

0°射角r1、r2夹角：

(26)

上下支点间的距离：

(27)

压缩行程：

Δl=l65-lj

(28)

相对于耳轴的力臂：

(29)

其中：(x1,y1)为A点初始坐标，(x2,y2)为B点坐标。

b) 重力矩Mqj

产生重力矩的质量分为相对为之随射角改变而改变的两部分：不含高平机筒的上部架体部分m1和高平机外筒部分m2，所以应采用变结构力矩的计算方法分析重力矩，得到动结构力臂：

(30)

总重力矩：

Mqj=mqglqcos(γ0+φj)

(31)

其中：lq1为上部架体重力相对于耳轴的力臂，lq2为外筒部分相对于耳轴的力矩。

c) 弹簧补偿力矩MTj

当φj>φc时，补偿弹簧才起作用，φc为补偿弹簧开始工作角度。

单个高平机弹簧力：

(32)

弹簧补偿力矩：

MTj=2k0(lj-l47)hj

(33)

其中k0为补偿弹簧刚度。

d) 平衡力矩Mpj

高平机容积：

Vj=V65-π(Rp2-Rn2)·Δl

(34)

单个高平机平衡力：

(35)

平衡力矩：

(36)

其中：V65为65°射角时的高平机容积，P65为65°射角时的高平机压强。

e) 紧塞部分摩擦力矩Mfj

紧塞部分摩擦力：

(37)

摩擦力矩：

(38)

其中：f1为平衡机密封圈与内筒的摩擦系数，f2为平衡机密封圈与螺筒的摩擦系数，d1为内筒外径，d2为螺筒外径，l1为内筒与密封圈接触长度，l2为螺筒与密封圈接触长度，c为修正项。

f) 有效平衡力矩

有效平衡力矩由平衡力矩、弹簧补偿力矩和紧塞装置摩擦力矩组成。其中弹簧补偿力矩是弹簧开始起作用时有效。摩擦力矩的方向与其运动趋势相反，所以火炮打高射角和打底射角的有效平衡力矩计算公式不同。

1) 当打高射角时，平衡机的有效平衡力矩为：

MHj=Mpj-MTj-Mfj

(39)

2) 当打低射角时，平衡机的有效平衡力矩为

MLj=Mpj-MTj+Mfj

(40)

g) 不平衡力矩计算

不平衡力矩为有效平衡力矩与重力矩之差，即：

ΔM=M有效-Mq

(41)

当有效力矩大于重力矩时，高平机处于过平衡状态；当有效平衡力矩小于重力矩时，高平机处于欠平衡状态。即打高射角时，过平衡状态下，螺杆受拉，螺母运动方向与其轴向受力方向相同；欠平衡状态下，螺杆受压，螺母运动方向与其轴向受力方向相反。向下打时，情况相反。

1) 当打高射角过平衡和打低射角欠平衡时，螺杆驱动力矩为：

(42)

2)当打高射角欠平衡和打低射角过平衡时，螺杆驱动力矩为：

(43)

h) 传动效率η与手轮力

通过传动效率和传动比，可将螺杆驱动转矩直接转化为改变射角时所需的手轮力。高平机手轮半径为R，传动比为i，由式(17)求得η，则手轮力计算公式为：

(44)

4 手轮力优化建模

传统的设计方法是根据总体方案的要求，选取不同的结构参数进行方案预算，因此，要想取得一个较为满意的方案往往要反复多次，而要取得最优方案就更困难了。前人尝试过的优化设计方法是在整个射界内多参数寻优，将最大不平衡力矩最小作为优化目标，但其优化设计模型过于简化，与实际相差较大，不易得到最优解，不能体现优化的真正意义。而文中优化得到的最优方案，可以为总体布置提供高平机的最佳参数匹配。

考虑传动系统中补偿弹簧和压缩气体的特性，结合相关结构、位置及特性参数，建立起高低系统整体力传递模型，推导力传动效率及手轮驱动力的计算公式，分析各可变参数对传递效率和手轮力的影响，并找出关键影响参数。以提高整体系统的传动效率，减小手轮驱动力，根据性能分析的结果合理配置设计变量，建立起高低系统的多目标性能优化模型，采用多学科优化软件iSight，对所建立的优化模型进行求解，以获得高低系统的最优力学性能。同时，对优化的结果进行分析评价。

考虑高平机压缩气体初始压强、体积，螺杆摩擦特性、弹簧补偿特性、结构尺寸等有关参数，对弹簧的设计计算、万向节花键联接轴的效率计算、传动效率匹配等方面分别建立独立的优化模型进行试验，验证模型的可行性。在此基础上进行设计变量的合理配置，同时以最大手轮力最小作为优化目标，建立高平机的参数化模型。

优化模型以高平机的位置参数、结构参数及特性参数为设计变量。考虑高平机压杆稳定以及螺杆行程需控制高平机上下支点最大距离的上限；高压气体密封的实际操作难度及由此所带来的附加摩擦力，控制高平机初始内部气体压力最大值的上限。以手轮力最大值最小为设计目标，优化设计的数学模型如下：

Objective=minFSLmax

S.T.:L≤Lmax

P≤Pmax

其中，FSL为手轮力，包括打高射角手轮力与打低射角手轮力，整个射角范围内手轮力最大值为FSLmax；Lmax与Pmax为约束条件上限。设计变量设置与说明如表1所示。

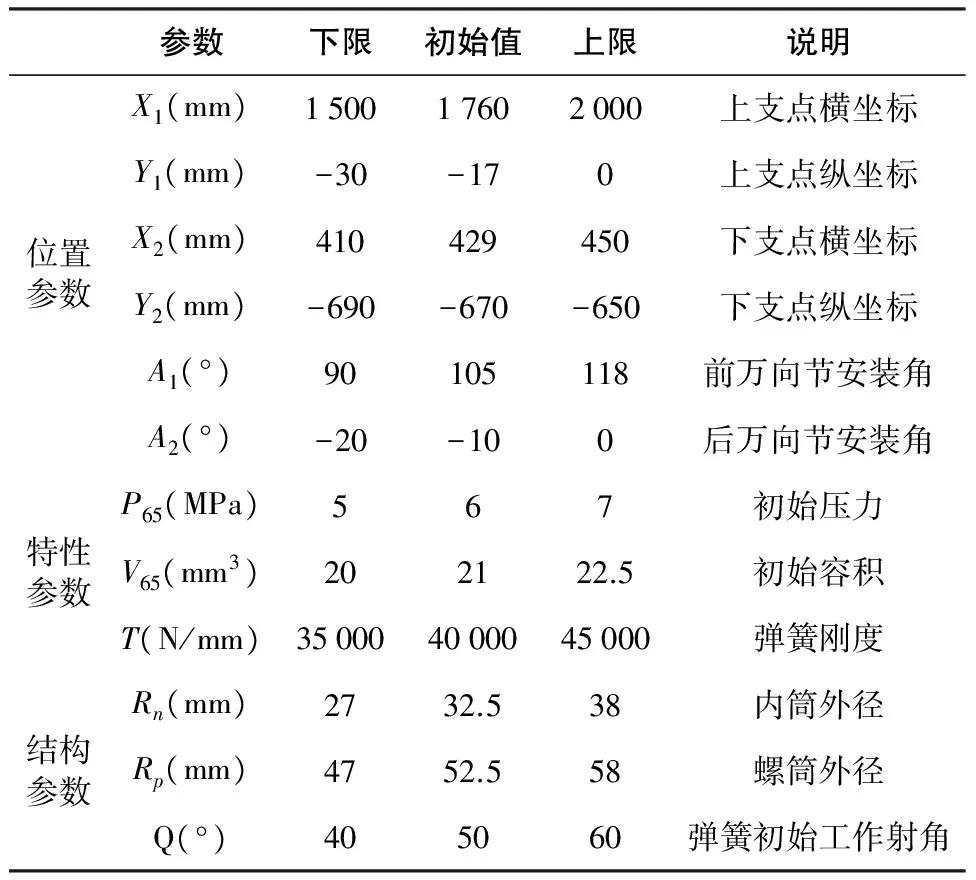
表1 优化设计参数表

5 优化前后结果对比

采用多学科优化软件iSight集成Matlab进行优化，优化的流程为：首先输入优化设计参数的初始值，调用一次Matlab进行计算，得到一轮手轮力数值，输出结果后采用遗传算法寻优，获得新的输入参数，重复上述优化流程，知道搜寻到全局最优解的大概位置，按经验选择一定的计算次数时开始采用胡克基夫算法进行寻优，其特点是较快收敛到最优解，提高效率。

本次计算共寻优14400次，耗时15h，进化历程图如图5。

图5 手轮力优化历程图

通过组合优化算法的寻优可得到全局最优解即可行域内手轮力最大值达到最小，将得到的参数值进行圆整并重新计算手轮力。表2为优化设计结果与传统设计结果的对比。

表2 优化设计参数表

手轮力曲线表示要使得火炮射角改变的力的大小，以及在射程范围内手轮力变化趋势。图6为将优化前后的曲线相对比的曲线图，可以看出优化后的曲线趋势变为平缓，变化范围大幅度减小，即最大手轮力明显减小。其中虚线代表打低射角时的手轮力，实线代表打高射角时的手轮力。优化前手轮力最大的时刻出现在打底射角65°的地方，且相当一部分射角的手轮力在150N左右，这会给实际操作带来较大的困难。而优化后的手轮力除不常用到的-3°射角之外，整个射程内手轮力均不到100N，且打高和打底射角时手轮力范围相当，体现出优化的明显效果。

图6 手轮力曲线

6 结语

针对火炮重要部件高平机进行了结构参数及特性参数的优化，通过多岛遗传算法与胡克基夫组合优化算法得到全局最优解，将手轮力的最大值降低60%，实际操作可行。

在某些靶场实验的情况下，高平机的结构及位置参数已经确定，此时可以实际装配情况为准将除初始容积、初始压强以外的参数作为定值，针对初始容积、初始压强进行高平机特性参数的单目标寻优，针对优化结果对高平机特性进行调整，及时的将手轮力控制在可操作的范围内。而文中的创新点在于，将高平机本体与传动系统同时考虑，较全的考虑各方面影响参数，研究对象是包括高平机本体部件、上部架体特性以及手轮传动在内的整个高低系统。

文中提出的机构建模模型方法不仅适用于高平机的优化设计，还可以应用于类似部件的计算分析。

[1] 张相炎,郑建国,杨军荣. 火炮设计理论[M]. 北京:北京理工大学出版社,2005.

[2] 孙靖民,梁迎春. 机械优化设计[M]. 北京:机械工业出版社,2006.

[3] 葛建立,过斌,杨国来，等. 基于参数优化的炮塔轻量化设计[J]. 火炮发射与控制学报,2011,(4):82-85.

[4] 蔡文勇,马福球,杨国来，等. 基于遗传算法的火炮总体参数动力学优化[J]. 兵工学报,2006,27(6): 974-977.

[5] 张训国,顾克秋,周成，等. 超轻型牵引火炮高平机优化设计研究[J]. 机械设计,2012,29(7):64-66,71.

Parameters Optimization of Elevating Equilibrator System of Gun

WANG Yanzhi, GU Keqiu

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094,China)

To reduce the manual hand crank force for lifting the barrel of the ultra-lightweight large caliber gun, parameter optimization method is utilized for designing the elevating equilibrator system. The relationship of the structure, position and characters of the elevating equilibrator system is established, and the manual hand crank force within the whole range is calculated through Matlab. Then a single objective optimal model is provided for minimizing the maximum manual hand crank force, and multi-island genetic algorithm and Hooke-jeeves direct search algorithm are both used to solve the optimization model. The optimized parameters of this model are obtained through the multidisciplinary optimization software iSight and Matlab. The results show that the optimal goal is achieved and the operability of the system is enhanced. It is of great significance in designing the elevating equilibrator system of the ultra-lightweight large caliber gun. Meanwhile, the optimization model also provides a new method for optimizing the general transmission systems.

Gun; elevating equilibrator (elevation counterbalance unit); optimization design

王妍智(1989-)，女，辽宁凌海人，本科，主要从事火炮设计研究。

TJ303

B

1671-5276(2015)05-0122-05

2014-02-24