计及布尔登效应的身管振动特性研究

朱大伟，周洁

(1. 中国舰船研究设计中心, 湖北 武汉 630064； 2. 振华重工有限公司，上海 200120)

计及布尔登效应的身管振动特性研究

朱大伟1，周洁2

(1. 中国舰船研究设计中心, 湖北 武汉 630064； 2. 振华重工有限公司，上海 200120)

弹丸发射过程中身管的振动对射击精度有很大影响，为了掌握身管振动的规律，将身管简化为悬臂梁模型，在此基础上建立了身管横向振动方程，运用模态分析法求解系统动力响应。针对某火炮不同装药量身管振动进行了数值仿真，对不考虑膛内气体对身管作用和考虑膛内气体对身管作用两种情况进行了比较。求解过程中弹丸的位移、速度和加速度均为实际数据。结果表明，静扰度对身管的振动特性有很大影响，静扰度为0时，弹丸初速越高，弹丸出炮口阶段炮口振动幅度越小，膛内气体对身管的作用力能有效减小发射期间身管的振动幅度。

火炮；身管；振动；模态分析；悬臂梁

火炮发射过程中，火药的燃烧所产生的物理和化学现象具有时间短、压力大、温度高等特点，同时，弹丸在膛内高速运动。由于这些作用具有瞬时冲击的特性，加上运动部件产生的惯性力作用，火炮必然会产生振动。身管的振动对火炮发射精度有较大影响，为了提高发射精度，必须减小振动。因此，对身管的振动研究就显得十分重要。

在研究身管振动时，一般将身管简化为一端固定，另一端自由的悬臂梁，将弹丸简化为一个移动质量。对于这类移动质量对梁的响应的问题的研究，早期主要存在于铁路、桥梁和工程机械领域。在国内，叶开沅等[1]针对列车过桥问题，建立了任意单个移动激励作用下铁路桥梁的动力学方程，并采用小参数法给出了方程的一般解；周叮等[2]将小参数法运用于火炮振动领域，研究了弹丸膛内运动引起炮管振动问题，并最终给出了单发及连发射击时炮管横向振动的一般解；姜沐[3]进一步建立了加速弹丸作用下火炮身管振动方程，并给出了级数形式的解析解和定量计算结果；史跃东等[4]在考虑惯性效应的基础上，研究了身管振动特性，给出了解析解，分析了不同运动参数对炮口振动的影响规律，给出了定量比较结果。到目前为止，大多研究都是将弹丸简化为匀速或者匀加速运动，也未考虑膛内气体对身管的横向作用力，对最终得出结论的精确性有一定影响。

1 身管振动方程及其解

身管力学模型如图1所示。弹丸沿炮膛轴线运动，其移动速度、加速度由实际弹丸的运动规律给出。

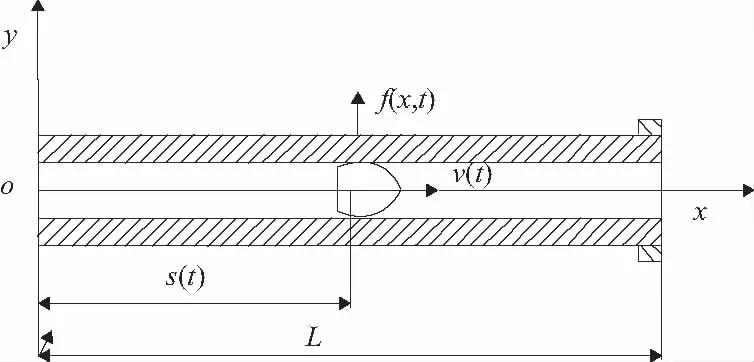
图1 身管横向振动受力模型

若不考虑阻尼，上述模型在任意时刻t，在横向载荷f(x,t)作用下的响应微分方程为[5]：

(1)

式中E、ρ分别为梁材料的弹性模量和质量密度，A、I分别为截面面积和截面惯性矩。

(2)

式(2)右端第1项为移动质量在弯曲梁上运动时对梁的横向作用力，第2项为梁右端集中质量的横向惯性力，第3项为梁内运动气体压力p(x,t)对梁的横向作用力。δ(x-L)和H(x)分别为狄拉克和阶跃函数。式(1)的边界条件为：

(3)

假定梁的响应可表示为：

(4)

(5)

(6)

式中Yi(x)为梁的第i阶振型函数，φi(t)为未知待求的时间响应常数，N为响应频率数。悬臂梁的振型函数Yi(x)为：

(7)

式(7)满足以下加权正交条件：

(8)

式(7)中的系数CYi由式(8)条件给出：

(9)

频率方程为：

cosλLcoshλL=-1

(10)

式(10)是一个超越方程，具有无穷个根λi(i=1,2,……)，在实际计算中取i的最大值为N。将式(4)、式(5)、式(6)带入式(1)，两边同乘以Yj(x)，在整个长度L上积分，并考虑到振型的正交性和狄拉克函数的特点，经整理得：

i=1,2,……N

(11)

式(11)是一组N个耦合微分方程组，可以将其表示如下矩阵形式:

(12)

其中：aii=1+mqYi(s(t))+MkYi2(L)，aij=MkYi(L)Yj(L)+mqYi(s(t))Yj(s(t))，

bij=Yi(s(t))Yj′(s(t))，

cii=-ωi2-mqv2Yi''(s(t))Yi(s(t))+

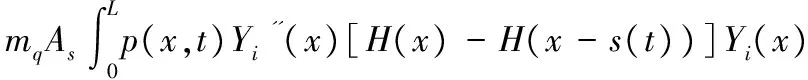
cij=-mqv2Yj''(s(t))Yi(s(t))+

di=mqgYi(s(t))

式(11)的初始条件由下式给出：

(15)

2 振动算例

考察全装药、一号装药、二号装药和三号装药4种工况，研究弹丸出炮口速度对身管振动响应的影响。同时，考察膛内气体以及初始静扰动对身管振动的影响。

火炮基本参数如下：弹丸的质量mq为21.76kg，身管长度L为4m，弹性模量E为2.1×1011Pa，材料密度ρ为7800kg/m3,截面惯性矩I为7.89×10-5m4，截面面积A为0.0219m2.

2.1 无初始位移

不考虑膛内气体对身管作用力的情况下身管振动仿真结果如图2、图3、图4所示。

图2 不考虑气体作用弹丸发射过程炮口位移

图3 不考虑气体作用弹丸发射过程炮口横向速度

图4 不考虑气体作用弹丸发射过程炮口横向速度

图2为不考虑气体横向作用力时炮口振幅y(L,t)的仿真结果，结果表明，随着装药量的增加，弹丸出炮口阶段炮口的位移随之减小。表1为不同装药量对应的弹丸初速下炮口的位移，可以看出随着弹丸初速的减小，炮口位移逐渐增大。图3、图4分别是炮口的速度、加速度仿真结果，图4表明在全装药时，身管受到动载荷最大，炮口的横向加速度幅值最大，其最大值达到1330m/s2。

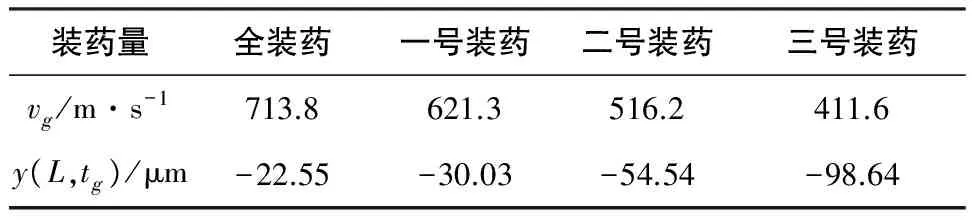
表1 不考虑膛内气体作用力不同初速时弹丸出炮口瞬间炮口位移

表1中vg为弹丸初速，tg为弹丸出炮口时间考虑膛内气体对身管作用力的情况下身管振动仿真结果如图5、图6、图7所示。

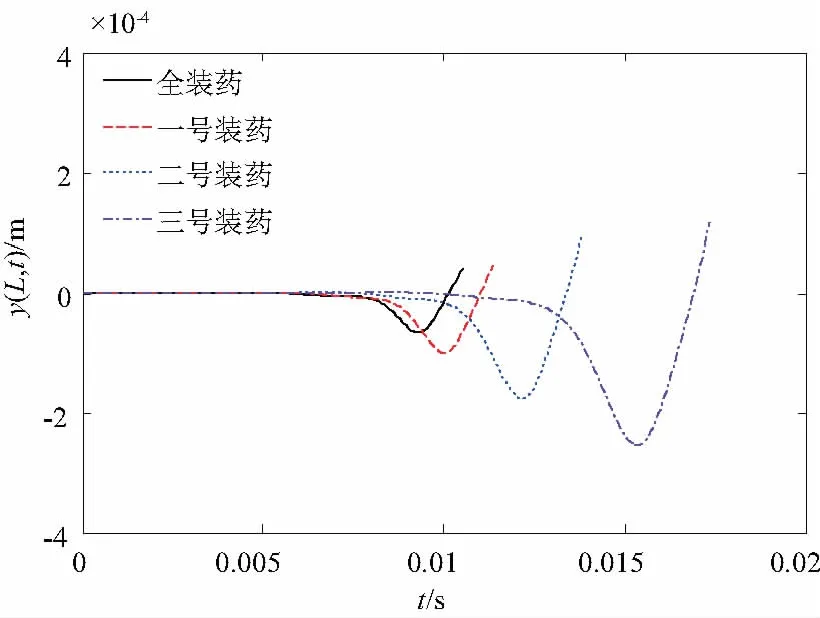
图5 考虑气体作用弹丸发射过程炮口位移

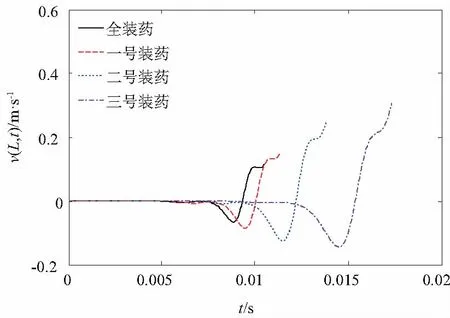
图6 考虑气体作用弹丸发射过程炮口横向速度

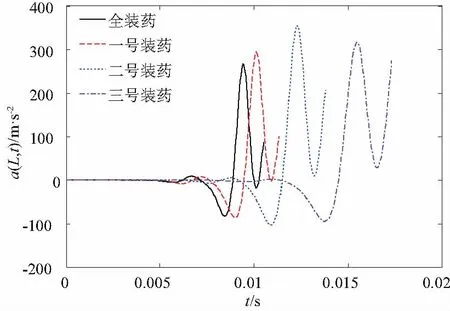
图7 考虑气体作用弹丸发射过程炮口横向加速度

图5为考虑气体横向作用力时4种不同装药量对应的炮口振幅y(L,t)的仿真结果。从图(5)中可以看出，其基本变化规律与不考虑膛内气体作用时炮口振动规律大致相同。通过式(2)不难发现膛内气体对身管的横向作用力方向与惯性质量对身管的横向作用力方向相反，起到了一定削减激振力的作用。比较图2和图5就会发现，在整个发射过程中，不考虑膛内气体压力对身管横向作用力时炮口的振动幅度明显大于考虑气体作用力的振动幅度。再通过比较图4和图7就能更清晰的反映装药量相同时第1种情况的炮口横向加速度远大于第2种情况的横向加速度，说明不考虑膛内气体作用力时身管受到的动载荷更大。

表2为不同装药量对应的弹丸初速下炮口的位移，从全装药到3号装药初速减小了42.34%，而弹丸飞出瞬间炮口振动幅度增大了172.39%。

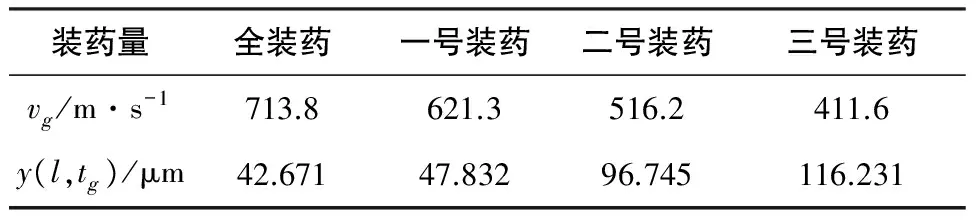
表2 考虑膛内气体作用力不同初速时弹丸出炮口瞬间炮口振动幅度

2.2 有初始位移

由于身管自重以及炮口制退器作用，身管在非发射状态时有一定静扰度。大多文献[3，4]在计算身管在发射时的振动位移时并为考虑身管的静扰度，文献[2]就直接将静扰度加动扰度直接相加得到身管的总扰度。经计算得到文中采用模型的静扰动为4.56mm，仿真结果如图8和图9所示。

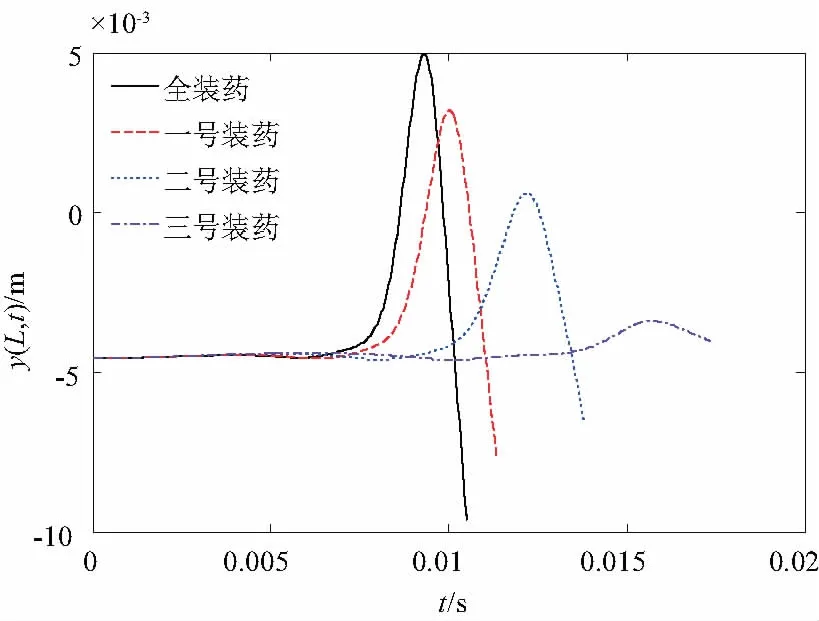
图8 考虑气体作用弹丸发射过程炮口位移

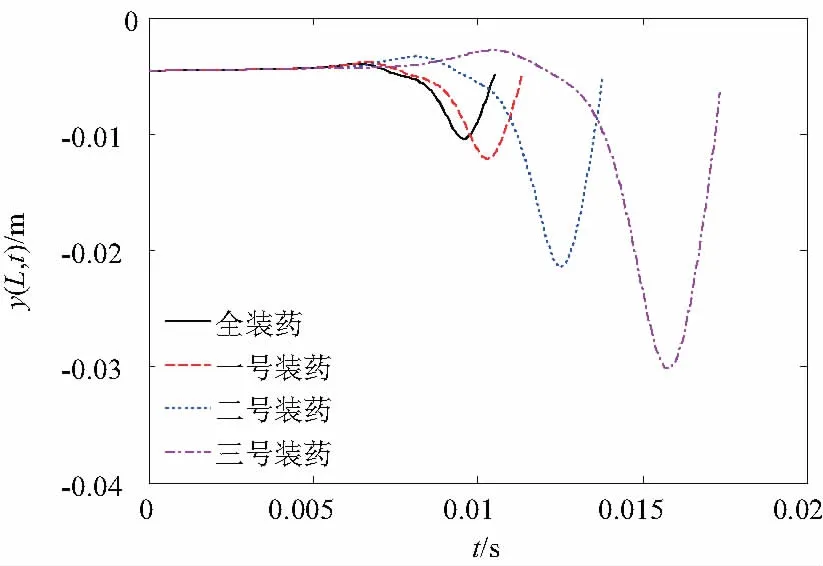
图9 不考虑气体作用弹丸发射过程炮口位移

图8为考虑气体作用几种工况的身管振动仿真结果，与图5比较就会发现，初始位移对身管的振动特性有很大影响。因为各阶时间响应函数之间有较强的耦合关系，所以初始位移对身管的振动特性影响较大。同时，身管的弯曲增大，Bourdon效应进一步增强，膛内气体对身管的横向压力也增大，所以，在不考虑膛内气体压力的情况下，炮口位移随时间的变化曲线形状并未有太大改变，而在考虑气体作用时，位移曲线的变化非常明显。

3 结语

在简化模型的基础上，建立了身管振动方程，对方程进行坐标变换，将受迫振动运动方程变换成用模态方程来表达。通过求解模态方程得到时间响应函数，从而得到身管振动横向位移以及速度、加速度响应。然后分别针对不同装药量进行了数值仿真，并且分析了膛内气体对身管横向振动的影响，得到主要结论如下：

1) 不考虑静扰度时，装药量越大，弹丸初速越高，其飞离炮口瞬间炮口振动幅度越小；考虑静扰度和膛内压力时，装药量越大，炮口振动幅度越大；考虑静扰度不考虑膛内气体压力时，装药量越大，弹丸出炮口瞬间炮口振动幅越小。

2) 炮口振动幅度变化对于初速变化较为敏感，在不考虑静扰度时，当初速减小了42.34%，弹丸飞出瞬间炮口振动幅度增大了172.39%，并且这种相对变化呈现出一种非线性关系。

3) 弹丸发射过程中，膛内气体的横向作用力有利于减小惯性质量对身管的横向作用力，因此不考虑膛内气体横向作用力时发射过程中炮口振动幅度更大一些。

4) 身管的静扰度对振动特性有较大影响，尤其在考虑膛内气体对身管的横向作用力时。

文中比较全面地考虑了身管的受力情况，采用模态分析法求解系统的动力响应。并以某火炮为对象，进行了数值仿真，得到了一系列弹丸发射过程中身管振动的规律。该方法同样适用于其他梁结构的受迫振动响应的研究。

[1] 叶开沅，马国琳. 计及行动载荷质量及惯性力影响的列车过桥动力理论[J]. 中国科学，1984，(4):338-352.

[2] 周叮，谢玉树. 弹丸膛内运动引起炮管振动的小参数法[J]. 振动与冲击，1999，18(1):76-81.

[3] 姜沐. 移动质量载荷在梁中激起的振动[J]. 力学与实践，2002，24(6):44-47.

[4] 史跃东，王德石. 考虑惯性效应的移动弹丸作用下身管振动特性[J]，2011，32(4): 414-420.

[5] 钱林方. 火炮弹道学[M]. 北京：北京理工大学出版社,2009:147-155.

[6] 刘荣忠，曹从咏.机械系统动力学[M]. 哈尔滨：哈尔滨工程大学出版社，2000：156-163.

Research on Vibration Characteristics of Barrel Considered Gas Pressure

ZHU Dawei1, ZHOU Jie2

(1. China Ship Development and Design Center, Wuhan 430064, China;2. Shanghai Zhenhua Heavy Industry Limited Company,Shanghai 200120, China)

The vibration of barrel has considerable influence on firing accuracy. To obtain the law of the barrel vibration, the barrel is considered as a cantilever in this paper, then its transverse vibration equation is established and the force response can be figured out by using modal analysis method. The vibration characteristics of the barrel are numerically simulated for different charge weight, besides, two situations the barrel with or without gas pressure are compared. In solving process, the displacement, velocity and acceleration of projectile are real datum. The simulation results indicate that static offset affects the vibration characteristics very much. The higher rprojectile′s initializing speed is, the smaller amplitude of the barrel′s vibration and effect of gas pressure are, which can decrease the amplitude of vibration considerably.

artillery; barrel; vibration; modal analysis; cantilever

朱大伟(1987-)，男，江苏扬州人，工程师，硕士研究生，主要从事火炮结构研究。

TJ303; TP391.9

A

1671-5276(2015)05-0058-04

2014-03-04