两栖轮式车辆用螺旋桨设计参数的确定方法
李 军,冯付勇,魏跃强,汪建兵,郭文珺
(中国北方车辆研究所,北京 100072)
两栖轮式车辆基于陆地行驶需要所具有的特定外形和行驶装置,与船舶构型差别显著,其特点为长度小、表面积小、形状变化突出,使其螺旋桨参数的确定与普通船用螺旋桨有很大的不同。两栖轮式车辆保持某一稳定的速度航行,是发动机、推进器和一定的车体外形三者相互匹配的结果。其中发动机是能量的提供者,车体则是能量的接受者,而推进器担负着转换器的角色,通过推进器的运转,使发动机的能量转换成车辆前进的动力[1]。因此,车体—螺旋桨—发动机之间能量转换及工作状态是相互牵制和相互关联的。
船舶其水线下船体的线型均严格按照流体力学特性设计,可以将水阻力效应减至最低,但是两栖轮式车辆为了兼顾陆上行驶,车体线型和船舶相去甚远,阻力系数远高于一般船舶,螺旋桨的负荷很大,本文将结合两栖轮式车辆的结构和使用特点,来分析其螺旋桨的设计参数如何确定。
1 螺旋桨推力的确定
两栖轮式车辆在水面航行时,螺旋桨的推力受到很多因素的影响,与发动机、水上传动装置、车体外形相互匹配有关,在已知两栖轮式车辆设计点的航速v0情况下,螺旋桨的有效推力Te等于车辆在航速v0时的航行阻力Rvo,即

由于两栖轮式车辆结构与使用情况与船舶差别显著,船舶理论中有关航行阻力的分析计算方法对两栖轮式车辆已不甚适用,而两栖轮式车辆的航行阻力Rvo包含3 种成分:摩擦主力Rf、形状阻力Rp、兴波阻力Rw。其中摩擦阻力只与湿表面积以及车体表面粗糙度有关,与车体的形状无关。形状阻力和兴波阻力是两栖轮式车辆行驶阻力的主要成分,而这2 种阻力在不同的水上航速时,其所占的比例是不同的,当速度较低时(有研究表明小于1.78 m /s ),以形状阻力为主;航速较高时(大于1.78 m /s ),阻力增加非常快,此时以兴波阻力为主[2]。两栖轮式车辆的航行阻力Rvo其值为

其中:
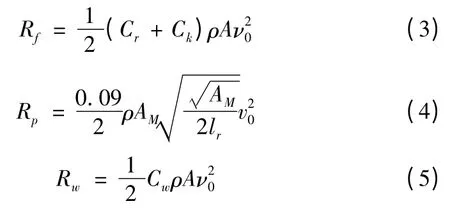
式中:Cr为摩擦系数;Ck为粗糙度系数;Cw为兴波阻力系数;AM为横剖面面积;lr为去流段长度;A 为车辆浸水表面面积。
通过式(3)~式(5)可得出
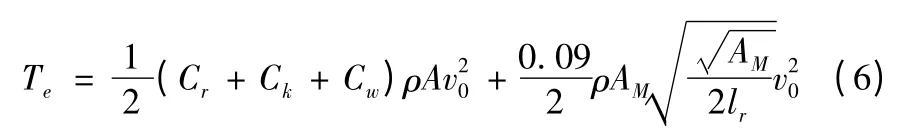
同时由于螺旋桨在车辆尾部工作时有吸水作用,使车辆尾部水流速度增大,如图1、图2 所示。

图1 管内流线

图2 管内速度矢量
根据伯努利定理,螺旋桨的工作引起车体总阻力的增加,损失了一部分螺旋桨推力,则设计螺旋桨需要的总推力值为

式中t 为推力减额系数。
通过式(1)、式(6)和式(7)可得出

两栖轮式车辆在水面航行时,其流体动力性能基本上取决于车体和行动部分的流体动力性能,以及它们之间的相互影响。当在已知两栖轮式车辆设计点的航速v0情况下,螺旋桨产生的推力与两栖轮式车辆在水上航行时的总阻力相等。水上航行速度对推力的影响较大,随着水上航行速度的增加,推力值成平方增加,不同车辆外形参数往往会导致阻力性能的变化,进而影响推力的大小。
螺旋桨推力的确定除了应用上述经验公式以为,还可以通过仿真计算求出。本文采用ICEM 对车体划分网格,生成的网格文件导入Fluent 软件进行求解。图3 给出了两栖轮式车辆在设计点航速时,两栖轮式车辆水中的姿态。图4 和图5 给出了车体表面的压力和动压的分布情况。可以看出:由于黏性和形体的原因,流场中出现了大量的漩涡,导致首尾形成压差。

图3 两栖轮式车辆航行姿态

图4 车体压力分布
图6和图7 进一步给出了中截面处流场的静压和动压分布。可以明显看到不同部位的受力分布。车体的首部出现了明显的高压区。车尾与车底连接的地方出现的低压区,这是由于此处的速度较高的原因。如果在此处改为平滑过渡,将有利于提高车体所受的升力。

图5 车体动压分布

图6 纵截面处压力分布

图7 纵截面处动压分布
本文采用隐式算法的求解器;多相流模型选用对自由液面进行追踪的VOF 模型,它对自由液面的追踪方法是几何重构的方法;湍流模型选用重整化的k -模型。算出车体表面的压力和摩擦力后,对车体表面记性积分,即可以得出车体所受的升力和阻力,然后通过式(1)、式(7)即可求出螺旋桨的推力。
2 螺旋桨叶数
螺旋桨叶数在2 ~6 之间。若直径和盘面比相同,则叶数少时效率较高,叶数多时则因翼栅作用较严重而使效率较低。严格来说,螺旋桨叶数的最佳选择必须用计算比较的方法来进行,比较简单的判定方法可以按照下述公式进行

当Kn≥1 时,叶片数选3;当Kn<1,叶片数选4。
但是,叶数对螺旋桨效率的影响并不严重,只是对振动、噪音和空泡等影响较大。从减小振动看,叶数多有利,但是当盘面比一定时,叶数增加会增加叶片截面厚度,容易发生空泡,所以从这个方面考虑,叶数以少为宜。另外,叶数多者,因为叶栅干扰作用增大,所以效率下降。
3 螺旋桨的转速及直径
水上推进装置的数量及其安装位置是由车辆水上航行时所需要的推力大小及车辆的总体布置决定的。两栖轮式车辆水上传动系统一般采用机械传动方案,螺旋桨通过与水上传动箱连接,把发动机输出的动力转变成水上推力,满足车辆在水上行驶的要求。螺旋桨转速的确定与发动机的转速和传动装置的传动比有关,两栖轮式车辆发动机的最大转速一般为2 200 ~2 500 r/min,考虑到水上传动箱的体积和质量因素,其传动比不宜过大,螺旋桨的转速初步选择在1 500 ~1 700 r/min 左右;若两栖轮式车辆水上传动系统采用液压泵马达方案时,泵与发动机自由端连接,螺旋桨与液压马达连接,把发动机输出的动力转变成水上推力,其螺旋桨设计转速比机械传动方案可提升15%左右。
螺旋桨转速的确定还应考虑螺旋桨直径的变化因素,螺旋桨的直径是进行螺旋桨设计的一个重要参数,螺旋桨的尺寸效应比较明显,按照螺旋桨推进理论,螺旋桨直径越大,转速越低,则敞水效率越高,但两栖轮式车辆用螺旋桨由于受两栖轮式车辆结构尺寸和车辆吃水的限制,其桨叶的直径不能超出车辆最大车宽,若螺旋桨直径过大将影响螺旋桨和车体的配合,使车身效率下降,对总的推进效率不利。
如图8 所示,根据两栖轮式车辆外形结构及总体布置,螺旋桨的直径要控制在浮箱甲板宽带以内。

图8 螺旋桨直径的范围
即

根据螺旋桨模型敞水试验,螺旋桨最佳转速为
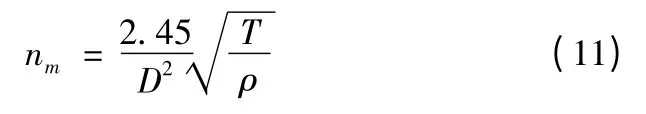
根据式(10)和式(11)可算出螺旋桨最适合的转速,其值为
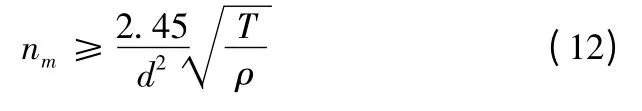
式中:D 为螺旋桨直径;T 为螺旋桨推力。
螺旋桨设计转速的确定还应考虑计算的空泡转速。当空泡发生在桨叶局部地方时,桨叶出现剥蚀现象。随着空泡的扩展,螺旋桨水动力特性受到影响,推力系数和转矩系数都较无空泡时为低[3],则不发生空泡其螺旋桨的临界转速为
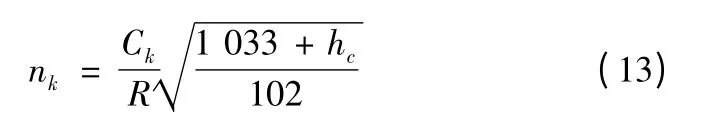
式中:Ck为空泡现象系数;R 为螺旋桨半径;hc为桨叶切面的沉没深度。
减小转速,可推迟空泡现象的发生,则螺旋桨设计转速为

由式(12)和式(14)可得出螺旋桨最佳转速

另外,两栖轮式车辆车体为薄壳车体,而薄壳车体结构为复杂的多自由度系统,所受的激励多为宽带激励,如果螺旋桨的转速过高,可能会引起车体共振,这样对螺旋桨的安装固定有更高的要求,需要采取有效措施减小振动峰值,加宽减振频率范围。
4 螺旋桨的螺距比
螺距比H/D 是螺距H 与螺旋桨直径D 的比值,是影响螺旋桨性能的主要因素,两个螺旋桨仅由于螺距比不同,其效率曲线就有明显的差别,螺距比越大,推力系数和转矩系数越大。当螺旋桨收到功率和转速一定时,螺旋桨直径越小,螺距比越大。但是螺旋桨的螺距比不能过大,螺距比过大容易产生空泡,并且不易加工制造,因此设计螺旋桨时应该综合考虑直径和螺距比的关系,尽可能优化最终设计方案。
在进行螺旋桨设计过程中,由于两栖轮式车辆对螺旋桨的直径尺寸限制较严,根据推力公式

当T 一定时,螺旋桨的直径根据总体布置的要求需要减小时,可通过提高转速或增大推力系数的方法解决。增加转速需要改变传动比,会增加水上传动箱体积和质量,这样会增加水上传动箱在总体方案中的布置难度,同时增大转速,会对螺旋桨的安装固定提出更高的要求,因此一般不会采用增大转速的办法,相应的采用增大螺旋桨的推力系数的方法。从图9 可知,当进速系数相同时,增大螺旋桨的螺距比可使桨叶的攻角增大,进而可提高螺旋桨的推力系数。
5 桨叶外型
桨叶外形轮廓对螺旋桨性能影响影响较小,其展开形状接近于椭圆型者为良好叶型。桨叶根部与桨毂连接处应采用大圆角过度,减小应力又减少涡流,保证螺旋桨效率。
螺旋桨常用的叶片截面形状有弓型和机翼型2 种见图10,弓型截面的压力分布均匀,不易产生空泡,在低负荷系数时,其效率比采用机翼型截片者低3% ~4%。根据螺旋桨桨叶静压表面分布图,如图11 所示,螺旋桨的叶片截面形状一般选择混合截面组合,即叶稍部分选用弓型截面,中段和根部选择机翼型截面。

图9 螺旋桨推力系数曲线

图10 螺旋桨桨叶外型
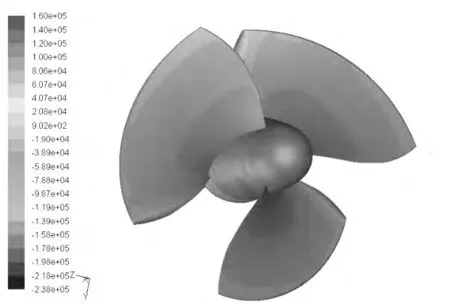
图11 螺旋桨桨叶静压表面
6 结论
从上述对两栖轮式车辆螺旋桨参数的分析中,对两栖轮式车辆用螺旋桨的设计有了进一步的认识,从中可以看出,对于两栖轮式车辆这种复杂的系统,其螺旋桨设计是多目标决策,重点在于和车体、发动机的多参数优化匹配,为此应尽快利用已经获得的数字模型和实车试验数据,进行模拟仿真对比研究,建立起比较完整的理论体系和设计方法,提高我国两栖轮式车辆用螺旋桨的设计水平。
[1]雷建宇,潘玉田,马新谋.两栖轮式车辆水上推进装置的研究[J].机械管理开发,2005(2):3-5.
[2]贾小平,于魁龙.减小两栖轮式车辆水上行驶阻力的方案探讨[J].装甲兵工程学院学报,1998(3):54-58.
[3]广东工学院造船系编写组.船用螺旋桨设计[M].北京:人民交通出版社,1976.

