射流冲击涡轮转子过程数值模拟

张际超，余 陵，蔡文祥，卓长飞

(南京理工大学机械工程学院，南京 210094)

为了使武器隐身性能更好，成本更低，适用范围更广，飞行器将向小型化发展。微型涡喷发动机作为小型巡航导弹和无人机可选动力装置之一，倍受各国关注［1］。微型涡喷发动机的启动是发动机整个工作过程的重要组成部分。

微型涡喷发动机的启动是指由零转速或者空中风车转速到慢车状态的过程。启动方式有火药启动、电机启动等［2］。刘建国［3］提出了一种新型启动方案，在涡轮盘端面加装端齿，通过火药启动器产生的燃气直接冲击端齿进而驱动涡轮。未发现针对该冲击流场进行分析的文献，本文将首次对此类问题进行研究。柯蒂斯·怀特公司设计的发动机，燃气发生器布置在中心锥内，燃气经外接管道流出，直接冲击涡轮;普拉特·惠特尼集团公司则将火药启动系统外壳设计成喷管中心锥，燃气经位于涡轮后部的4 个超音速喷嘴冲击涡轮［4］。基于刘建国提出的方案，本文采取将固体推进剂燃气发生器置于微型涡喷发动机的中心锥内的结构布置方式;分别选取双石-2 推进剂;以及某低燃速低燃温双基推进剂(该推进剂为针对秦能等［5］的研究成果，选取其中序号为5D的双基推进剂配方);并通过从燃烧室末端引出的两个成循环对称分布的斜切喷管，喷出燃气，冲击涡轮端齿，完成启动。本文采取的方案，优点在于可以使得结构更加紧凑;燃气冲击涡轮盘端面的端齿，避免燃气对涡轮叶片的直接冲刷和烧蚀。转子的启动加速，实质为角加速度不断改变、角速度不断增加的运动。取足够小的微元时间，可认为转子匀速转动，本文即针对5 000 rev/min 进行研究。为了了解启动器的启动性能，需要得到转子所受到的驱动扭矩大小。所以应当得到转子在不同转速、不同位置的驱动扭矩的大小，接着通过回归分析方法［6］，得到完整的启动器的驱动力矩-时间关系。

本文针对冲击射流对涡轮端齿的作用，采用CFX 软件进行数值模拟，将整个流体域分为了包含盘面的旋转域以及其他静止不动的外场域，通过动静交界面对两个流体区域进行连接。分析了盘面以5 000 rev/min 转动，边界不断变化的瞬态冲击流场;得到了由冲击载荷所引起的扭矩随转子转动的变化规律，以及扭矩的大小;针对其中一个位置的流场，分析了流场中的激波结构。

1 物理模型与工作原理

1.1 物理模型

启动装置组件包括燃气发生器筒体、引管、斜切喷管等;转子的组件包括涡轮、螺母、轴承、轴、压气机等。图1 为物理模型示意图。

图1 物理模型

图2为气斗结构图，气斗指的是由端齿面、周向斜面、端面、径向斜面、齿顶面这5 个面组成的面组;盘面指的是由总共10 个气斗组成的面组。

图2 气斗

盘面最大外圆半径为21 mm;斜切喷管入口直径为5 mm;喉部直径2 mm;扩张比为2。喷管扩张段之后接等截面斜切长尾管;斜切喷管轴线与引管中心轴线所夹锐角为65°;喷管斜切面到涡轮凸台距离为4 mm。

1.2 工作原理

启动装置中的固体推进剂被点燃，产生高温高压的燃气分别经过两个引管进入斜切喷管，在斜切喷管中燃气膨胀加速冲击到气斗诸面上。只考虑燃气所具有的动能，粗略采用动量定理，得到单个斜切喷管射流冲击到端齿面上的气动力方程

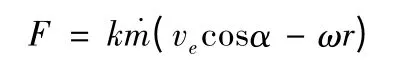
2 流场计算模型与计算方法

2.1 流场计算模型

图3 所示为斜切喷管内流场计算模型，本着循序渐进的原则，首先对其进行计算，意图获得喷管性能参数。

针对图4 所示全流场计算模型，模型由外场域与旋转域组成，两者之间由动静交界面连接;图4 中给出了坐标系;沿顺时针方向对1 ～10 号气斗进行标号(图4 中仅给出气斗1、2、3 的位置);不考虑微型涡喷尾喷管对来自盘面气流的限制作用。

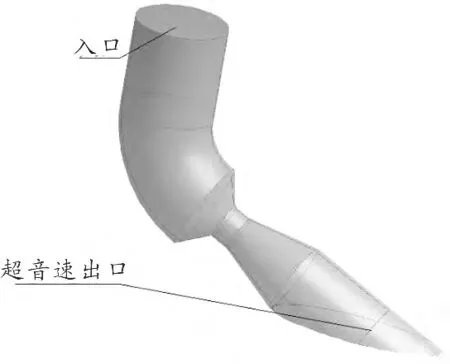
图3 斜切喷管内流场计算模型

图4 全流场计算模型

针对上述两模型进行网格划分，采用非结构四面体网格，并对近壁面处加密。得到如图5、图6 网格示意图。其中斜切喷管内流场计算模型共划分15 万网格;全流场计算模型分别采用120 万以及190 万网格。对全流场模型不同网格数的模型进行准稳态试算，结果显示:两者出口质量流率、涡轮盘总扭矩、轴向载荷等差异均在1%左右，故选用120 万网格。

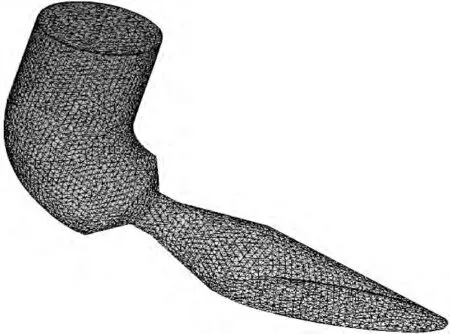
图5 斜切喷管内流场计算模型网格

图6 全流场计算模型网格

2.2 边界条件

采用双石-2 推进剂与某低燃速低燃温双基推进剂;圆柱形推进剂内外孔同时燃烧;基于内弹道的计算结果，得到单个引管入口的气动参数，如表1 所示。因为两入口的总温不同，故分别称为高温入口与低温入口;两入口总压基本相等;其中质量流率由斜切喷管内流场计算得到。表2 为全流场四次计算中的边界条件设置。

斜切喷管内外壁、燃烧室底部、螺母、盘面为壁面，设置为绝热、无粘。高温、低温全流场计算中:转速设置为5 000 rev/min;持续时间为0.003 6 s;时间步长3.75e-5 s;开放式出口位置为如图4 所示的外圆柱面;全流场的初值计算时，交界面采用Frozen Rotor;随后非定常计算时交界面采用 Transient Rotor Stator 。

2.3 计算方法

流场计算均采用SST 湍流模型;基于有限体积法对非定常雷诺平均的Navier-Stokes 方程进行离散;对时间导数项的离散采用二阶向后欧拉差分;对流项采用高分辨率格式。

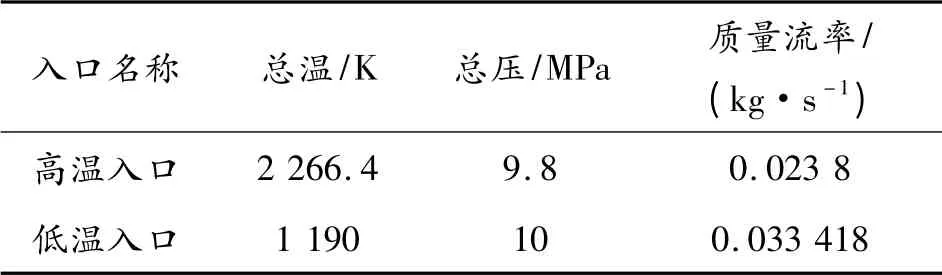
表1 高温与低温入口

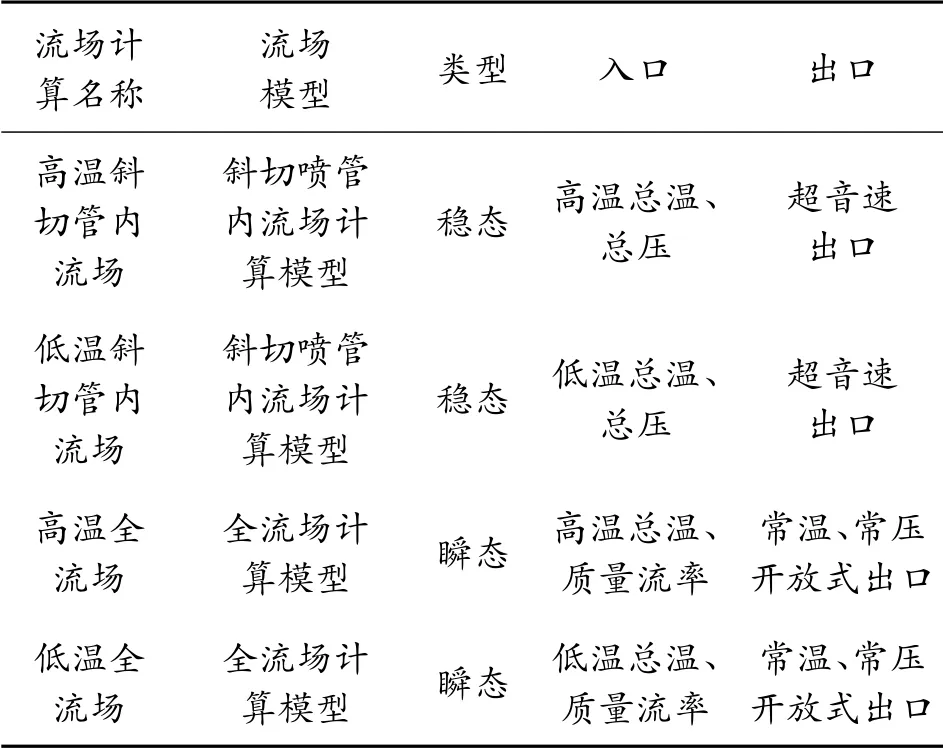
表2 计算域边界条件

3 斜切喷管内流场计算结果与分析

表3 给出了斜切喷管的性能参数。高温、低温斜切管内流场计算采用基本相等的入口总压，主要区别在于入口燃气温度的高低。出口平均马赫数、压比、推力等基本相等，说明这些参数主要是由斜切喷管的结构尺寸以及入口总压决定;在喉部达到临界状态的情况下，低温斜切喷管内流场计算中的燃气温度较低，所以其出口质量流率更大;排气速度正比于燃烧室的燃气温度，温度越高排气速度越高，温度由2 266.4 K 降低47.5%达到1 190 K 时，出口平均速度降低了27.3%;由于未切长尾管壁对气流流动的约束以及管内斜激波的作用，推力矢量方向偏离斜切喷管中心轴，偏向已切除管壁一侧。

表3 斜切喷管性能参数

4 全流场计算结果与分析

4.1 冲击载荷所引起的盘面扭矩变化规律

图7 ～图10 给出了气斗1 ～5，选取其中不同面，组成的部分，受到射流冲击所引起的扭矩随盘面转动的变化规律。本节将会讨论扭矩曲线的周期性、曲线移动的重合性以及增减性，作为讨论流场激波结构、流动状态以及启动器启动性能的基础。图4 给出了气斗1、2、3 的位置，初步猜测，随着盘面的转动，气斗1 至5 将会受到来自斜切喷管1 的射流冲击。接下来首先给出图7 ～图10 并作简要介绍，之后综合起来研究扭矩的变化规律。

图7 所示，为低温全流场计算中气斗2、3、4 的端齿面与周向斜面扭矩图。横轴:观察图4 所示全流场计算模型，从z轴正方向看向z 轴负方向，盘面沿顺时针方向转过的角度φ;图4 所在位置即为起始角度0°;因为盘面以5 000 rev/min 匀速转动，所以φ =30 000 t;应当注意到，在任意一个时间点，对应唯一一个从0°转到当前位置的角度。纵轴:例如M4_dc表示端齿面4 的扭矩，从z 轴正方向看向z 轴负方向，沿顺时针方向扭矩取正值;M4_zx表示周向斜面4 的扭矩。

图7 端齿面与周向斜面扭矩

图8为气斗1 至5 在高、低温全流场计算中的扭矩图。纵轴:例如Mdw_4表示低温入口条件下，4 号气斗的总扭矩(任意角度Mdw_4=M4_dc+M4_zx，忽略齿顶面、径向斜面、端面上产生的扭矩，因为上述3 个曲面，产生扭矩主要依靠气流与面间的黏性摩擦力，大小非常小);Mgw_4表示高温入口条件下，4 号气斗的总扭矩。

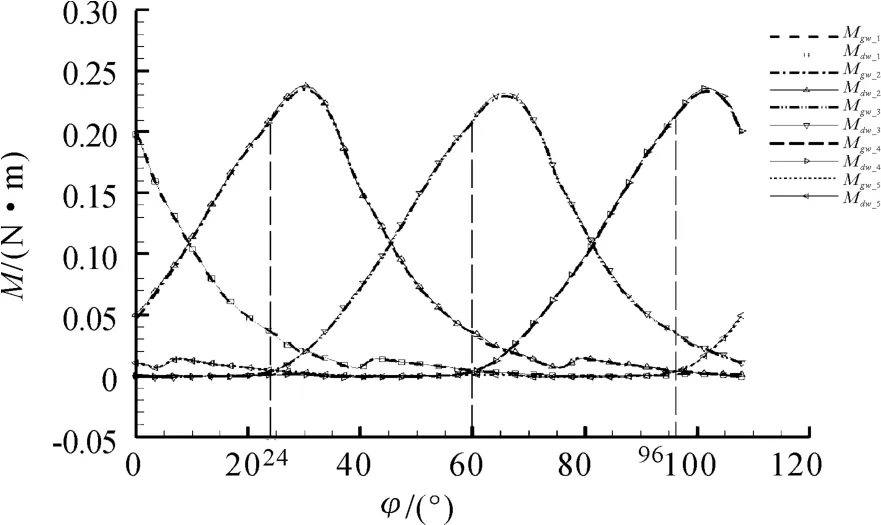
图8 单气斗扭矩

图9所示为高、低温全流场计算中组合气斗与盘面扭矩图。纵轴:例如在任意角度下Mdw_345=Mdw_3+Mdw_4+Mdw_5，Mdw_345表示低温入口条件下3、4、5 气斗扭矩之和;Mdw_pm表示整个盘面的总扭矩大小的一半。

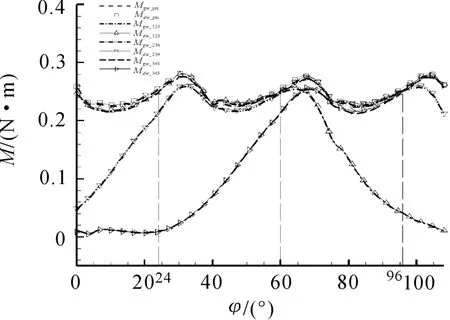
图9 组合气斗与盘面扭矩

图10(a)、(b)分别表示低温入口条件下气斗1、5 表面平均压力。纵轴:pdc、pzx、pdm、pjx、pcdm依次是端齿、周向斜面、端面、径向斜面、齿顶面的表面平均压力。

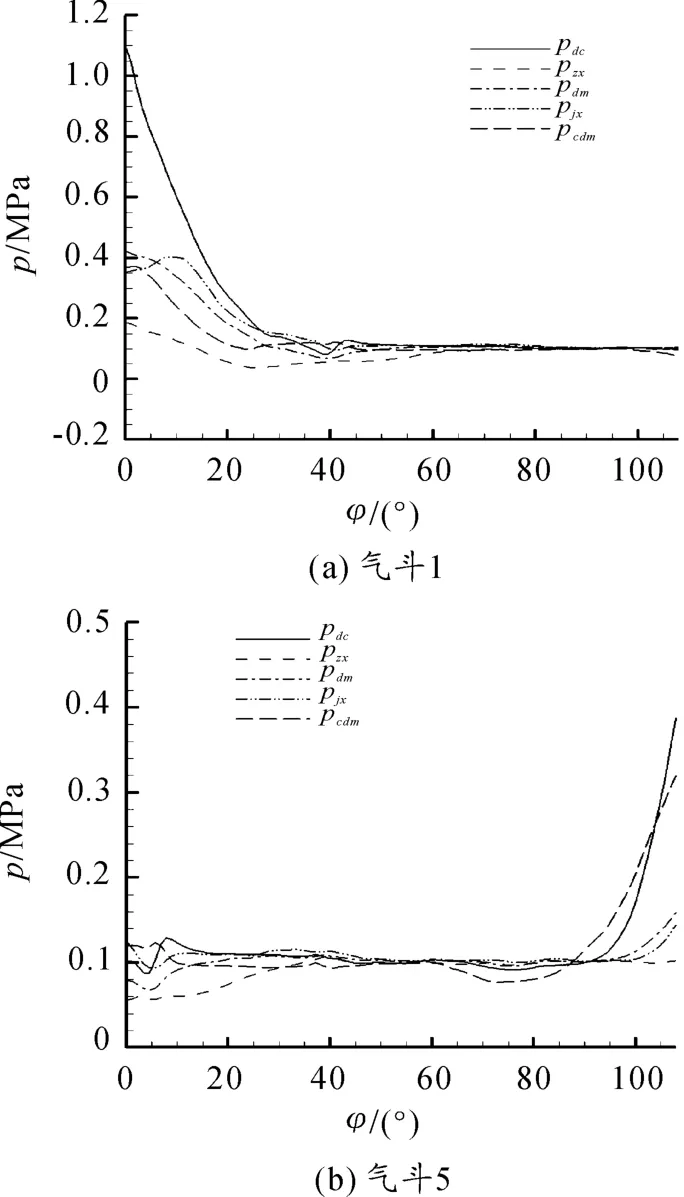
图10 气斗表面压力

观察图8、图9 高温与低温入口条件下计算所得曲线完全重合。所以在物理模型几何尺寸确定的情况下，冲击载荷大小主要由转速、所在角度、入口总压决定。从喷管出口喷出的相同质量的燃气，高温入口条件下燃气的做功能力更强;在推进剂低燃烧温度的基础上，提高燃烧温度，可以减少推进剂的消耗量，但会使得涡轮承受更大的瞬态热载荷。

由于高温与低温入口条件下的扭矩曲线完全重合，所以以下仅观察图7 至图10 在低温入口条件下的扭矩曲线。由0 至60°，图10(a)气斗1 表面的压力下降并趋近于一个大气压，与此同时图8 的Mdw_1也逐渐趋近于0，说明气斗1 逐渐离开射流影响范围;60°至108°，图10(a)气斗1 表面压力保持一个大气压，与此同时图8，Mdw_1=0，说明气斗1 没有受到气流冲击，在大气压影响范围;60° ～96°，图10(b)总体上气斗5 表面压力保持在一个大气压左右，与此同时在这段区间内图8 的Mdw_5=0;从96°开始，图10(b)气斗5 表面压力开始升高，图8Mdw_5由0 开始增大，表明气斗5 进入了射流影响范围。

大气压影响范围的存在，说明单个气斗在结束一个斜切喷管的冲击过后需要转过一定角度才能受到另一个斜切喷管的作用，即单个气斗不可能同时受到来自两个斜切喷管的冲击射流。因为360°内分布了两个斜切喷管，所以得到一个普遍规律:一个气斗拥有5 个面，任选一个气斗，任选5 个面中任意个面的组合，该组合所受冲击载荷的变化周期为转180°所用的时间，这段时间可以分为大气压影响范围和射流影响范围两个区间;所以图7 中，例如曲线M4_dc与M4_zx的变化周期均180°;图8 中，例如曲线Mdw_4周期为180°。盘面总共有10 个气斗，因为盘面匀速转动，那么全流场的边界形状的变化周期为转36°;所以当前全流场的形状与再转36°以后的全流场的形状一样。所以如图9 曲线Mdw_pm的变化周期为36°，且在这个周期内，盘面一直处在射流冲击的作用下。

图7 中，由全流场形状变化的周期性，可知曲线M4_dc向横轴负方向移动36°与M3_dc重合;同理图8 中，曲线Mdw_5向横轴负方向移动36°与Mdw_4重合;图9，Mdw_345向横轴负方向移动36°与Mdw_234重合。其他的曲线具有类似的性质。

图8 中，60° ～96°范围内，在不是非常严格的情况下，有且只有Mdw_2、Mdw_3、Mdw_4不为0;并且根据图8、图10，气斗1 ～60°进入大气压影响范围，气斗5 在96°刚刚离开大气影响范围;在图9 中，60° ～96°范围内，Mdw_pm=Mdw_234，说明在这一范围内，只有气斗2、3、4 受斜切喷管1 的射流冲击;同理，96°到132°为气斗3、4、5，以此类推。

所以只需要描述60°到96°范围内气斗2、3、4 的扭矩，便可得知盘面在这个周期内扭矩变化的机理。根据上述的曲线移动的重合性，可以得知，图8，96° ～132°区间内的Mdw_4向横轴负方向移动36°便与60° ～96°区间内的Mdw_3重合;图8，132° ～168°区间内的Mdw_4向横轴负方向移动72 度便于60° ～96°区间内的Mdw_2重合，说明单个气斗从进入射流影响范围到离开总共要转108°。

从图8 可以看出Mdw_4曲线的增减区间和最值、极值。在60°取得最小值0;随后扭矩增大，在101.8°取得最大扭矩0.235 N·m;之后持续减小，最终在168°扭矩变为0;所以对气斗4 来说，射流影响范围是它从60° ～168°之间。图9，Mdw_pm曲线呈现周期性震荡波动，最大扭矩0.277 N·m;最小扭矩0.227 N·m。

图11 所示，针对3 个角度位置，具体分析气斗2、3、4 表面压力分布的情况;由图9 可知以下3 个角度分别位于曲线Mdw_pm增减区间端点，φ=67.5°时Mdw_pm处于最大值。

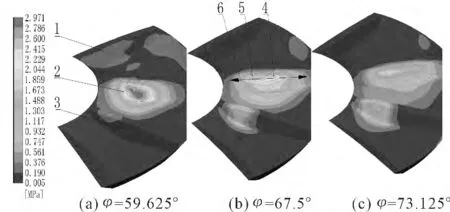
图11 不同角度盘面压力

图11(a)、(b)、(c)中端齿3，以及图11(b)、(c)中的端齿4，等压曲线呈现出一个个椭圆形的环形区域依次嵌套而成，各个环形区域总体上是呈现出由最大压力点向四周，压力递减的过程;盘面由59.625°转到73.125°的过程中:端齿2 表面压力逐渐恢复到大气压;端齿3 上，压力在2.79 MPa到2.97 MPa 范围内的高压区域面积逐渐减小，并向靠近轴线的方向移动;端面3 上压力逐渐增大;端齿4 上表面压力及燃气气流作用面积也逐渐增大。

图11(b)中，射线1 与射线2 的起点均为最大压力点，且射线1 与射线2 共线;取射线1 的方向为正方向，射线2 的方向为负方向，最大压力点为0 mm 位置，在该直线上做出压力随位置的变化曲线，如图12 所示的压力分布曲线。

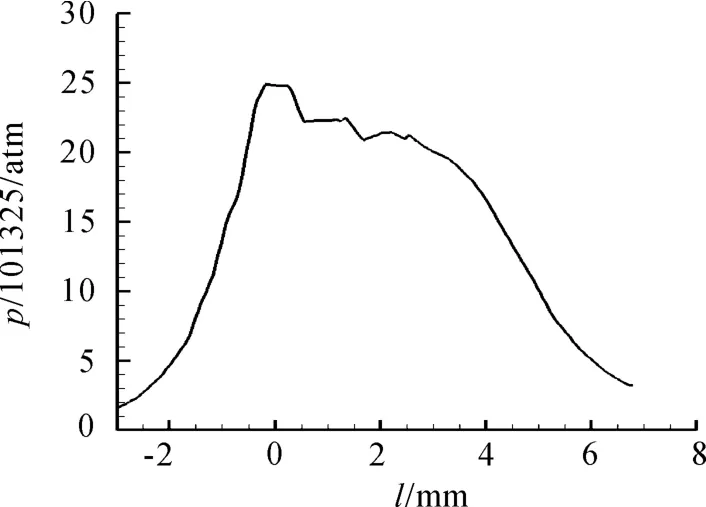
图12 压力分布曲线

从0 mm 位置开始，沿着横轴负方向，压力迅速下降，主要是由于大部分气流沿横轴正方向流动;沿着横轴正方向0.6 ～2.8 mm 范围内压力降低较小，有两小段压力平台期;2.8 mm 之后压力迅速下降。

4.2 冲击流场激波结构

随着盘面的转动，不同角度的流场的某些相同的区域，拥有不同的气动参数。图13 ～图16 均为φ =67.5°角度位置流场，该角度盘面扭矩最大。

图13 所示超音速三维马赫图显示了流场的全貌，图中给出了1 ～4.5 马赫范围。根据三维马赫图，整个流场可以分为如图几个明显的流动区域，整个流场内燃气气流的流动路线是:亚音速气流由引管进入斜切喷管，经斜切喷管扩张段膨胀加速，离开斜切管内流场;由于是欠膨胀气流，所以气流在第一自由射流区继续膨胀加速;气流接近壁面时，速度下降，并且改变流动方向;气流离开冲击区，沿壁面流动形成壁面射流;最后气流离开壁面进入第二自由射流区。

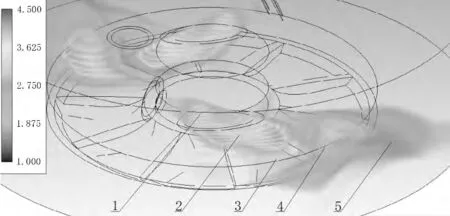
图13 超音速三维马赫图

图14 为斜切喷管纵切面马赫图，图中给出了激波的位置。

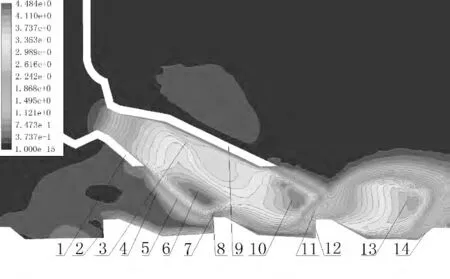
图14 斜切喷管纵切面马赫图

以下将从斜切喷管内流场、第一自由射流区、冲击区、壁面射流区、第二自由射流区5 个部分并结合各部分局部图对图14 进行解释说明。

斜切喷管内流场:斜切喷管未切管壁将会反射来自管内射流边界的膨胀波，形成压缩波，由于扇形膨胀区的扩散性质，使得壁面发生的众多弱压缩波，聚集成斜激波，气流向切去管壁的方向发生偏转;该斜激波影响了整个第一自由射流区，使得第一自由射流区出现了两个膨胀波区;靠近已切除管壁一侧的气流没有流经斜激波，气流经扩张段膨胀，由于是欠膨胀气流，所以在第一自由射流区继续膨胀，形成第一膨胀波区，气流作用于端齿4。靠近未切除管壁一侧的气流经过了斜激波，波后速度减小，压力增大，但气流流出喷管进入第一自由射流区后，会膨胀加速，形成了第二膨胀波区，作用于端齿3。

第一自由射流区:由于斜喷管出口气流处于欠膨胀状态，气流喷出出口后会继续膨胀加速，在出口附近产生膨胀波，膨胀波遭遇射流边界后反射，形成由斜激波组成的相交激波，最终气流冲击到盘面，端齿3、4 上产生脱体激波，脱体激波直接影响了第一、第二膨胀波区。

冲击区:根据图15 流线图以及图16 端齿3 速度矢量图可知，整个端齿3、端面3 表面基本均处在冲击区范围内。

图15 流线图

图16 端齿3 速度矢量图

如图15、图16 还可以发现:冲击到端面面3 和周向斜面3 上的气流改变方向继续冲击到端齿面3 上;冲击到端齿面3 上的气流还有一部分来自自由射流的直接冲击;端齿面3表面的气流一部分沿着图11(b)射线1 方向流动;冲击到端齿3 上的另一部分气流跨过端齿3，流动到气斗2。相对于气流射流的规模，端齿的尺寸较小，此部分流动类似于楔形体受冲击问题;端齿3、4 上均产生脱体激波，激波后气流速度迅速降低到亚音速，气流方向发生偏转，流线图与速度矢量图都可看出，气流流动方向以不同的曲率逐渐向外转折，该区存在很大压力梯度。

壁面射流区:该区主要位于气斗2，不过气流的流动实际上还要受到径向斜面2 的阻挡;沿着主流流动方向，气流膨胀加速，形成了第三膨胀波区;沿着端面2 的法线方向，随着距离端面2 的距离的增加，气流速度先增大后减小。

第二自由射流区:最终气流离开壁面射流区进入第二自由射流区，随后离开开放式出口。

5 结论

本文首次对射流冲击涡轮转子端齿的冲击流场进行了研究，探讨了研究方法，得出了以下结论:

1)物理模型几何尺寸确定的情况下，冲击载荷的大小主要由转速、所在角度、入口总压决定，而与入口总温关系不大。此结论可为燃气发生器设计提供参考。

2)单个气斗是受到射流冲击的基本单元，随盘面转动，单个气斗将经历射流影响范围-大气压影响范围-射流影响范围的循环过程，一个周期需要单个气斗旋转180°。观察者随斜切喷管静止不动，一个斜切喷管射流的影响范围是冲击区附近的相邻的3 个气斗，由于有两个斜切喷管，即任意时刻总共有6 个气斗瞬间处在射流影响范围，4 个气斗处在大气压影响范围。盘面总扭矩随时间成周期性震荡变化，变化周期为盘面转36°所用的时间。在总扭矩变化的特定的周期内(以24°为起点，依次每隔36°进行划分，得到24°至60°，60°至96°等等区间)，有且仅有6个端齿受到了燃气持续的冲击。驱动转子旋转的盘面总扭矩的大小约为0.5 N·m。此结论描述了涡轮盘面受到的冲击载荷的作用机制。

3)斜切喷管未切管壁反射出斜激波，造成自由射流区存在两个超音速膨胀波区。φ=67.5°角度位置流场，在端齿3、4 上方的脱体激波直接分别影响到两个超音速膨胀波区。为了了解不同角度位置，流场结构的差异，需要进行更多的研究。

［1］谭汉清.国外微型涡喷发动机应用现状及未来发展趋势［J］.飞航导弹，2013(3):76-80.

［2］郑严，厐重义.弹用涡喷(涡扇)发动机技术［J］.飞航导弹，2001(12):43-52.

［3］刘建国.弹用涡喷发动机快速启动涡轮结构设计与分析［D］.长沙:国防科学技术大学，2011.5.

［4］Walker D W. Navy Development of Low Cost Supersonic Turbojet Engineer ［J］. Naval Weapons Center，SAE 730362，1973(4):101-107.

［5］秦能，汪亮，王宁飞.低燃速低燃温双基推进剂燃烧性能的调节［J］.火炸药学报，2003，26(3):16-19.

［6］王娟.对统计中相关分析与回归分析的论述［J］.现代经济信息，2014(8):115.