一种基于模糊算法的军用车辆发动机故障诊断模型

【后勤保障与装备管理】

一种基于模糊算法的军用车辆发动机故障诊断模型

王大军1，韩建礼2

(1.后勤学院后方专业勤务系，北京100858； 2.装甲兵工程学院训练部，北京100072)

摘要：为方便技术人员和乘员提高军用车辆发动机故障诊断、故障排除的效率和准确率，采用模糊集合算法，汇集专家经验，建立了军用车辆发动机故障诊断模型，包括建立诊断矩阵、模式识别、问诊、自适应修正，实际诊断结果证明了所建模型的合理性和可信性。

关键词:模糊算法；军用车辆发动机；故障诊断

收稿日期：2014-10-20

作者简介：王大军(1966—)，男，副教授，主要从事后勤保障与装备管理研究。

doi:10.11809/scbgxb2015.03.019

中图分类号：TP206+.3;TJ81

文章编号：1006-0707(2015)03-0071-05

本文引用格式：王大军，韩建礼.一种基于模糊算法的军用车辆发动机故障诊断模型[J].四川兵工学报，2015(3):71-75.

Citation format:WANG Da-jun, Han Jian-li.Fault Diagnosis Model of Military Vehicle Engines Based on Fuzzy Algorithm[J].Journal of Sichuan Ordnance,2015(3):71-75.

Fault Diagnosis Model of Military Vehicle Engines

Based on Fuzzy Algorithm

WANG Da-jun1, Han Jian-li2

(1.Rear Services Department, Academy of Logistics, Beijing 100858, China;

2.Training Ministry, Academy of Armored Force Engineering, Beijing 100072, China)

Abstract:In order to improve the efficiency and accuracy of military vehicle engine fault diagnosis and troubleshooting, the paper established a model based on fuzzy algorithm and experts’ experience, including diagnosis matrix, pattern recognition, inquiry diagnosis, adaptive correction. The actual diagnosis results prove the rationality and reliability of established model.

Key words： fuzzy algorithm; military vehicle engine; fault diagnosis

军用车辆发动机发生故障具有极大的复杂性和随机性，野外训练和野战条件下不具备携带专业检测设备的条件，发生故障后往往依靠人的经验判断故障成因，迅速排除或修理。专家或具有丰富经验的人根据模糊的故障现象和长期积累的经验，可以快速准确地诊断出发动机故障原因。但积累丰富经验必须经过大量实践历练，需消耗巨大精力和大量时间。如果把专家的知识和经验储存起来加以集成，使一般技术人员和乘员可迅速借用专家经验，具有可观的军事效益和经济效益。采用模糊集合论算法，汇集专家经验，建立军用车辆发动机故障诊断模型和诊断系统[1]，可以帮助乘员和技术人员提高故障诊断和故障排除的准确率、效率。利用模糊算法建立发动机故障诊断模型，包括建立诊断矩阵、模式识别、问诊、自适应修正等[2]。

1诊断矩阵与模式识别

建立基于模糊算法的诊断模型，需做大量准备工作。通过走访专家、技术人员和富有经验的乘员、维修人员，仔细进行机理分析，把引起这些故障现象的成因列举出来，包括收集发动机故障，分类整理故障现象和故障成因，给出故障成因排除方法，并确定故障现象、故障成因之间的相互关系。对引起同一个故障现象的不同成因，由于引起的现象一样，可归为一个故障成因。如“外组油箱连接管堵塞”、“油路堵塞”、“柴油粗、细滤清器脏污”，它们引起的现象都是大负荷工作时功率不足，故把它们归为一类。对于“排气开关不密闭”等成因，也可能造成发动机大负荷工作时功率不足，但这和油路堵塞供油不足不是同一类性质的原因，应另行归类。一般讲，成因分得越细诊断结果越准确，但往往造成诊断矩阵过大而得不出诊断结果。控制故障成因个数，可以增加成因与现象的交叉，发挥模糊算法的特长和优势。

通过分类整理故障现象和故障成因，就可建立起征兆成因矩阵。如某成因可能引起某征兆(故障现象)发生，则在矩阵中的对应值为1，否则为0，这样布尔矩阵便产生了。

1.1隶属函数的确定

布尔矩阵只表示成因和征兆之间存在因果关系，不能表示发生的可能性大小，还需结合专家打分和已有资料，采用模糊算法确定矩阵中数值的大小。建立故障诊断模型就是要根据布尔矩阵建立诊断矩阵，以隶属度的形式反映矩阵中征兆和成因之间的关系，并用模式识别方法得到诊断结论。

隶属函数的确定方法有统计法、加权统计法、二元对比排序法等[3]，加权统计法比较真实地反映实际情况。用加权统计法确定诊断矩阵中某元素的隶属函数uij，主要考虑4种因素，即经验统计资料(l1),机理分析(l2)，征兆出现的明显程度(l3)，获得该征兆的难易程度(l4)。第一因素l1的评分可直接从统计资料得到

式中：Nxi、NAj分别为处置方法正确的总次数与在此条件下征兆xi出现的次数。第二、三、四因素的评分，可事先按下面的征兆语言值所对应的从属度对每一具体征兆请大量专业人员给出评分(见表1)。

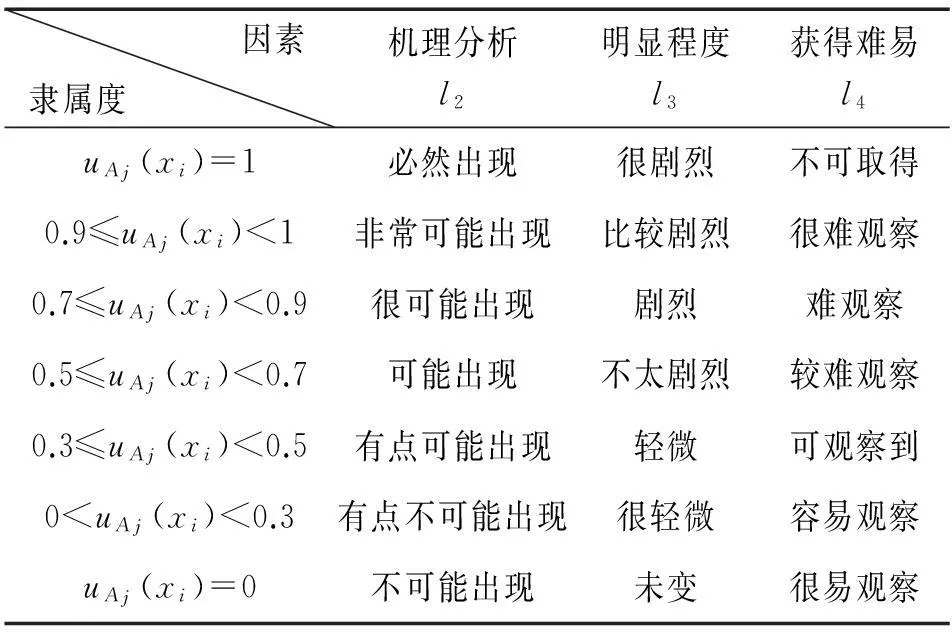
表1　征兆语言与隶属度关系表

每一具体征兆的评分集合表示为

由每一征兆的评分集合与权数集合计算得到相应的隶属度uij

上述算式得到的隶属度一般偏高，且很容易丢失其中权重分配小的因素，如明显程度、获得难易程度的评分，下面算式能比较真实反映实际情况

1.2诊断过程

诊断过程实际上是模式识别的过程，就是模拟人的思维方法，根据输入的征兆群[4]，得出诊断结论(成因)。

1.2.1模式识别方法选择

确定了诊断模型及隶属度计算方法，就可以进入编程，完成故障诊断系统界面，根据提示输入征兆群[5]，计算各成因的隶属度，从大到小得到各成因优先次序，隶属度最大的成因发生的可能性最大。实际诊断过程中，为进一步区分隶属度相差不大的成因，一般输出几个结果。

从征兆群的输入到输出诊断决策结果，模式识别的任务便已完成，但这只是搭起了系统的“骨架”，要使系统不断完善，还需要有问诊和自适应修正等不可缺少的重要环节。

2问诊

实际诊断过程中，由于现场人员观察不仔细，或限于技术水平观察不到或描述不恰当，或有些故障征兆不易发现，造成所提供征兆有遗漏或错误，模型难于确诊或输出[6-7]。应通过问诊，有针对性地自动询问对诊断最有价值且尚未录入的征兆。

2.1问诊时机

按输入征兆群对应各成因的隶属度从大到小进行排序，如果最大隶属度数值与其他隶属度数值差值较大，且满足阈值输出条件，做出该征兆群属于该成因的结论是可信的。但如果得到的前几个成因的隶属度很接近，若以排在最前面的成因作为诊断结论就值得怀疑，模糊集合论的观点认为此时排在前面的几个成因发生的可能性几乎相等，从这几个成因中选出一个作为诊断结论，需进一步提供征兆，即需进一步问诊。另外，如果隶属度不满足阈值输出条件，也需进一步问诊。

(问诊1条件)或

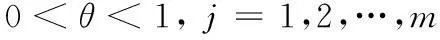
(问诊2条件)，则需问诊。

α、θ是事先选定的阈值。0和1是两种最清晰的状态，取它们中间值0.5是最模糊的。但固定阈值0.5并不能满足输入征兆群个数变化的要求，有必要使α的值随输入征兆个数变化而变化。可依下式变化：α=0.5-0.015(n-1)，斜率0.015由系统调试得出，n为输入的征兆个数。θ值由实践得出，θ值不表示某个方案采取的可能性的大小，而只是表示了前几个方案发生可能性的相差程度，不必要随输入征兆个数的变化和问诊次数的增加而变化。只要前几个成因相邻隶属度之差≥θ，说明分辨度够，可以输出结果，否则需要问诊。θ值可调试确定(本模型θ取0.1)。

2.2问诊过程

问诊过程是根据计算结果决策输出结果还是进入问诊程序，是进入问诊1还是进入问诊2。

基本步骤：确定对象集X和因素集U，找出评判矩阵R，确定评判函数f：D=f(z1,z2,…,zm)， 按Ⅰ′、Ⅱ′、Ⅲ′型评判函数综合评判。

第Ⅰ′型：D1=(z1+z2+…+zm)/m

第Ⅱ型：D2=(z1∨z2∨…∨zm)

第Ⅲ′型：D3=(z1∧z2∧…∧zm)

m为判据集中元素个数。计算评判指标：

将D(x1),D(x2),…,D(xm)按大小排序，按序择优。

2.2.1因素集和对象集的确定

问诊过程因素集(判据集)U={计算的最大隶属度，隶属度差值，阈值α是否达到，分辨度(差值)θ是否达到}，对象集X={输出，停止问诊，问诊1，问诊2}。输出和停止问诊是明确概念，可根据阈值和分辨度等条件编程控制，对象集简化为X={问诊1，问诊2}，即综合评判的任务是要确定决策转向问诊1还是问诊2。

2.2.2评判矩阵的确定

确定了因素集和判据集，可得评判矩阵(见表2)。

表2　评判矩阵表

表2中数据确定：如果umax≥α且umax-uj≥θ，则输出结果，否则进行综合评判。如果umax<α，umax越小，1-umax就越大，对进入问诊1的影响大，对进入问诊2的影响小，同时给问诊1的权值大(0.6)，问诊2的权值小(0.4)，反之亦然。如果分辨度<θ，umax-uj愈小，r2[1-(umax-uj)]愈大，对进入问诊2的影响大，相应给问诊2的权值大(0.6)，问诊1的权值小(0.4)，反之亦然。表中r1、r2是考虑到umax-uj值一般较小，而1-(umax-uj)较大，为满足整体综合评判的需要，需对它们进行调整，其值由实际调试确定，如r1=4.5、r2=0.4。

2.2.3评判指标

Ⅰ′、Ⅱ′、Ⅲ′型评判函数都只是取了问题的一个方面，即取平均，或取最大，或取最小。对综合评判问题，还可分别求出D1、D2、D3，视它们为因素集中的元素，利用它们再做一次评判，即所谓二级评判[3]。如果已知对象集X、因素集U及评判矩阵R，则S=(X,U,R)称为评判空间。设评判空间为S=(X,U,R)，按Ⅰ′、Ⅱ′、Ⅲ′型计算得：

令U1={D1,D2,D3},R1∈F(X×U1)，即可得一新的评判矩阵：

其中xi为备选对象集，本模型中即为问诊1和问诊2，F(X×U1)表示论域X×U1上模糊集合的全体。于是得到了一个新的评判空间S1=(X,U1,R1),对S1再做一次评判，评判函数可设为：

计算di=f(di1，di2,di3),i≤m，称di为xi的评判指标，从di中排序择优。

D1,D2,D3为一次评判后的结果，可取其均值作为评判指标。令a1=a2=a3=1/3，则

综合评判举例：已知计算结果umax=0.45，uj=0.4，求评判结果。隶属度和分辨度均不满足输出条件，评判矩阵为：

按Ⅰ，、Ⅱ，、Ⅲ，型计算得R1如下：

d1

2.2.4问诊方法

如进入问诊1，说明输入的征兆不充足，应对诊断决策贡献最大的征兆提问；如进入问诊2，则对两个隶属度之差最大的征兆提问。

算法2：主要解决umax-uj<θ的问题。设给定一征兆群B={xi,i∈I1}，计算结果Ac、Av两个方案的隶属度非常接近，则在诊断矩阵中提问B中未出现过，且对应Ac、Av两个方案隶属度差值最大的征兆，计算差值：Wl=|ulc-ulv|(l∈I0)。式中I0为B中未出现过的征兆下标集合。取Wg=max{wl，l∈I0}，提问与之相对应的xg征兆。

2.3自适应修正

诊断决策矩阵汇集了专家的排故经验，但是，专家也有可能在某些方面判断的正确性不够，甚至在某些方面有错漏。诊断决策过程中需要不断获取新的知识，或者修改原有知识，使自身不断完善，即模型要有自学习的功能[8]，自动修正诊断矩阵中的隶属度值，在不破坏典型故障和模型故障诊断经验的基础上，使得诊断结果向正确的方向转化，在保证诊断矩阵稳定、收敛的同时，使诊断结果更加符合客观实际。为了不破坏原有诊断矩阵的正确性和稳定性，自适应修正过程中还需要检验典型诊断实例和实际排故经验，但不需要检验其全部，只需要检验与自修正最相关的典型实例或排故经验[9]。如果修正后不破坏最相关的典型实例，认为自适应修正是稳定、收敛的。

3故障诊断实例

通过建立某型坦克发动机故障诊断矩阵，进行故障诊断，并和实际排故结果比较，证实模型给出的结果与实际相符。

实例1：某部一辆坦克训练完毕回场途中，发动机逐渐无力至缓慢熄火，启动数次无效。排除喷油泵空气时，发现有大量空气，排气后能顺利启动，但工作一段时间后又自行熄火，多次反复。

实例2：某坦克在野营拉练中，突然听到“呛呛呛”的响声，怀疑单缸供油量大，更换了新喷油泵，但声音并未消失；启动时发现空气滤清器内有吱吱的压缩空气冲出的声音。诊断结果如表3和表4所示。

表3　诊断实例1

4结论

本模型采用模糊算法建立的评判矩阵及所确定的评判指标，能比较满意地得出评判结果，确实使故障诊断向有利的方向发展，证实了本模型的合理性和可信性。问诊次数超过3次时自动跳出问诊，为了给用户提供较多的问诊信息，每次问诊都显示排在前面的3个征兆，提高了诊断的准确率，而且诊断速度并不降低。

参考文献：

[1]王松岭.坦克发动机故障诊断专家系统研究[D].辽宁：大连理工大学，2005.

[2]贺仲雄.模糊数学及其应用[M].天津：天津科学技术出版社，1983：16-20.

[3]汪培庄.模糊集合论及其应用[M].上海：上海科技出版社，1983：14-17.

[4]黄开启，黄跃飞，刘晓波.多征兆模糊诊断系统知识表示及专家系统研究[J].中国机械工程，2004，15(12)：1077-1079.

[5]宋平，苏万华，裴毅强，等.柴油机模糊诊断专家系统研究[J].内燃机工程，2007，28(4)：65-68.

[6]王久崇，樊晓光，万明，等.改进的故障树模糊诊断方法及其应用[J].计算机工程与应用,2012，48(14)：226-230.

[7]李宇，王伟平，刘博宁，等.基于故障树的复杂电子系统可靠度模糊评定方法[J].计算机测量与控制，2010，20(9)：2467-2469.

[8]WANG ZHONG-HAO,SHAO XIN-YU,ZHANG GUO-JUN.Integration of Variable Precision Rough Set and Fuzzy Clustering:An Application to Knowledge Acquisition for Manufacturing Process Planning[M].Springer,Berlin,Heidelberg,2005：585-593.

[9]齐怡，沈士团，李驿华.模糊诊断规则自学习中规则条件优选技术研究[J].北京航空航天大学学报，2004，30(06)：506-511.

(责任编辑杨继森)