航空装备更新模型优化

【后勤保障与装备管理】

航空装备更新模型优化

苏涛1，曹文静1，郝梦媛2

(1.海军航空工程学院 控制工程系，山东 烟台264001；

2.烟台大学 计算机与控制工程学院，山东 烟台264000)

摘要：针对装备最佳更新时机的问题，建立装备更新模型，并把时间的价值因素考虑进去改进装备更新模型，使计算结果更加准确，显著提高军事效益。

关键词：装备更新；最佳时机；时间价值

收稿日期：2014-08-15

基金项目：国家自然科学基金资助(61203168)

作者简介：苏涛(1979—)，男，讲师，硕士，主要从事军事物流信息化研究。

doi:10.11809/scbgxb2015.03.022

中图分类号：O221.3;TJ-9

文章编号：1006-0707(2015)03-0084-03

本文引用格式：苏涛，曹文静，郝梦媛.航空装备更新模型优化[J].四川兵工学报，2015(3):84-85.

Citation format:SU Tao, CAO Wen-Jing, HAO Meng-Yuan.Optimization Model of Aviation Equipment Renewal[J].Journal of Sichuan Ordnance,2015(3):84-85.

Optimization Model of Aviation Equipment Renewal

SU Tao1, CAO Wen-Jing1, HAO Meng-Yuan2

(1.Department of Control Engineering, Naval Aeronautical Engineering Institute, Yantai 264001, China;

2.Department of Information and Computational Science, YanTai University, Yantai 264000, China)

Abstract:Aiming to solve the problem on optimal timing of updating equipment, the equipment renewal model was established by taking the time value factor into account, which makes the results more accurate and improves military efficiency significantly.

Key words: equipment renewal; the best time; time value

武器装备的更新是指新装备代替到寿退役的旧装备，以满足给定装备总量和结构的要求[1]。当新装备与旧装备型号相同时，更新的运筹问题在于如何确定装备更新周期(即服役到退役的间隔时间)[2]。当新装备对旧装备而言是更新换代产品时，这种更新又称为换装[3]。这时的运筹问题在于确定换装经历时间，各年换装量以及在给定年度换装数量指标下，各部队间的换装比例[4]。下面讨论同型号装备更新的运筹问题。

1预备知识

1.1最佳更新周期

一方面，随着使用年限的增加，武器装备的损坏和老化程度会越来越严重，平均每年用于维修的费用会逐年增加[5]；另一方面，由于武器装备的购置费用是一次确定的，其年均购置费会随着使用年限的增加逐年减少[6]。因此，武器装备的更新周期直接影响着总费用(购置费与使用维修费之和)的大小。从经济效益角度来讲，要选取一个最佳的更新周期，使平均每年所消耗的总费用最小[7]，如图1所示。

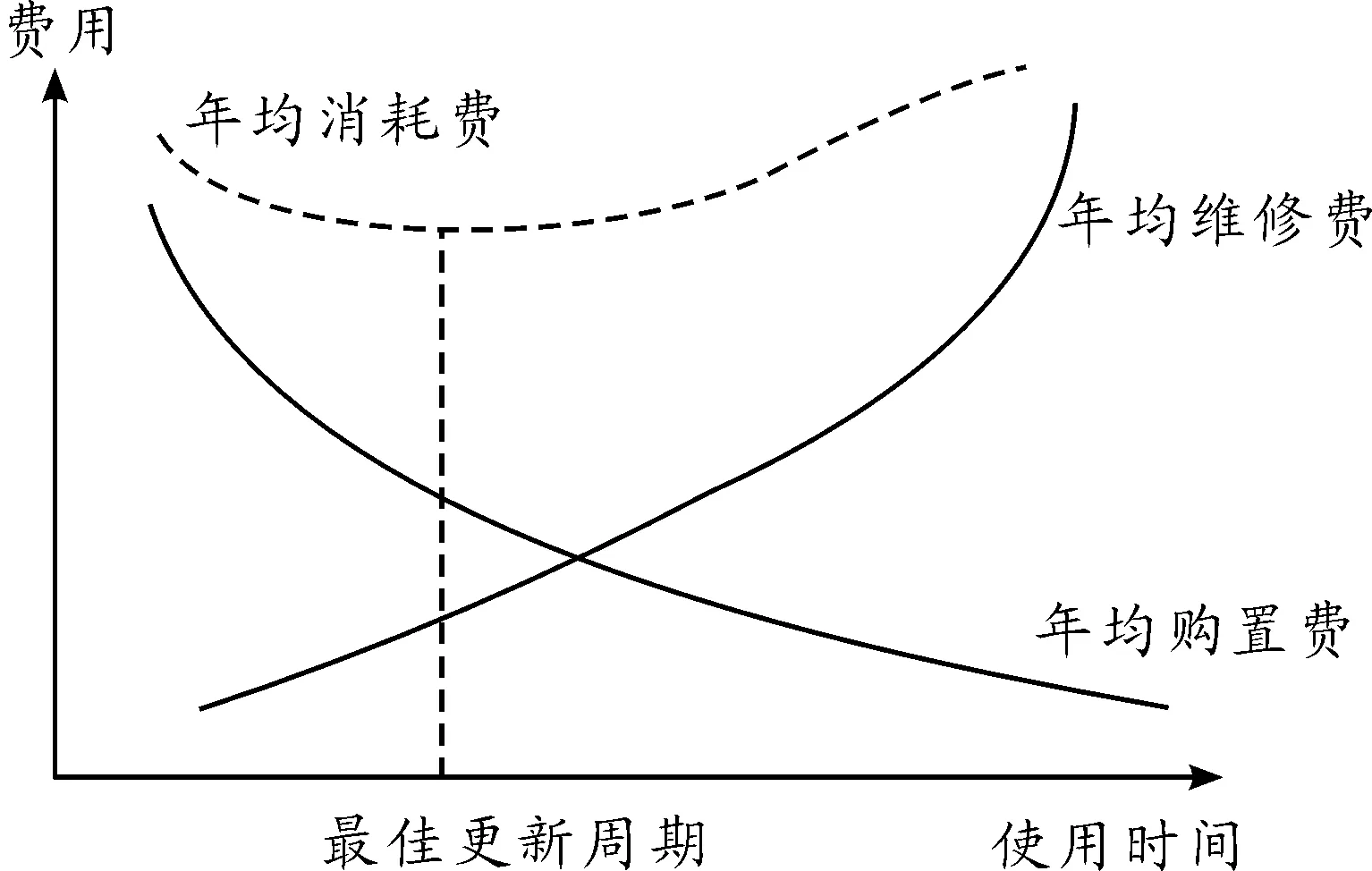
图1　最佳更新周期的概念

1.2使用寿命

装备的使用寿命是指规定的使用期限，达到这个期限，装备就要退役，并用同一型号的新装备来补充[8]。而装备的使用寿命根据其确定原则有不同含义。通常分为自然寿命(装备从开始使用到由于实体发生损坏、老化直至报废所经历的时间)[9]，技术寿命(从投入使用到由于更高功能装备的出现而被硬性淘汰所经历的时间)[10]和经济寿命(从投入使用到其经济效益低于使用新装备所经历的时间)[11]。

一般情况下，经济寿命是确定装备使用寿命的主要依据。而且，对于某种类型的武器装备，技术寿命最短，经济寿命次之，自然寿命最长[12]。

2装备更新模型

假设装备原始购置费为J，使用年限为n，则其年均购置费为

(1)

又设装备维修费逐年递增，依次为f, 2f, …,nf，则n年维修总费用为

(2)

装备年均维修费为

(3)

装备使用n年，年均总费用为

(4)

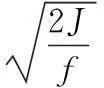
3改进的装备更新模型

在以上的模型中，为了使问题简化，我们并没有考虑时间的价值因素。一般情形下，费用的时间价值是由费用折扣率来体现的[13]。考虑这一点，在计算维修费总和时，应将各年支出的维修费换算为现值；而计算平均年消耗费用时，应将现值换算为各年度平均支出费。

各年度费用换算为现值的公式为

(5)

其中:F0为第0年现值；Fn第n年支出的费用；r为平均年利率。

现值总额与各年度平均消耗费用的换算公式为

(6)

其中：G0为n年消费耗用的现值总额；gc为年平均消耗费用。

应用上述2个公式后，年均消耗费用式(4)改为

(7)

式(7)中：gn表示更新周期为n时，未来各年平均消耗的费用；Fi表示第i年支出的费用。显然，使gn取最小值的n便是最佳更新年限。

4实例求解

某型航空装备原始购置费为10 000，第一年维修费用为800元，其后每年维修费用以800元的幅度递增，平均年利率为10%，试求该型航空装备最佳使用年限。

1) 假设不考虑时间价值因素，最佳更新周期应为

这时年均总费用F有最小值为

2) 改进后的最佳更新年限，根据题意，r=0.1,Fi=800i,J=10 000,代入式(7)得

计算得当n=6时，gn最小，gn=4 375。

5结果分析

由计算结果可以看出， 考虑了时间的价值因素的模型结果与之前的有所变化。费用的时间价值因素的确存在，不容忽视，改进的模型的结果更准确。而且，最佳更新年限和年均总费用的变化和平均年利率的取值有关。

改变平均年利率r的值，最佳更新年限和年均总费用的值则如表1所示。

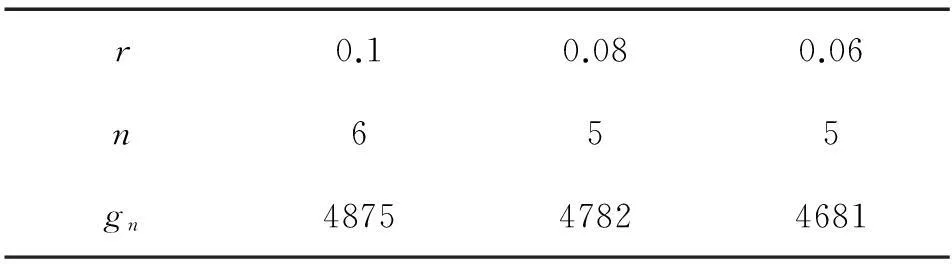
表1　年均总费用随 r变化

6结束语

从经济效益的角度来看，武器装备一旦到了最佳更新周期，就应当立即更换[14]。从表面来看，装备还可以用，每年需要的维修费也很少，好像延迟一年更新就能节省一年的购置费，其实是将购置费的紧张转嫁到维修费上去了。由此可见，确定准确的装备最佳更新周期很有必要，把费用的价值因素考虑进去，保障了结果的实用性和准确性，确保武器装备发展规划的实现，

参考文献：

[1]王铁宁.装备管理信息系统原理与应用[M].北京：国防工业出版社，2013.

[2]郭文晖.军事装备管理创新[M].北京：国防工业出版社，2010.

[3]赵经成，祝华远，王文秀.航空装备技术保障运筹分析[M].北京：国防工业出版社，2010.

[4]张丽叶.装备更新经济性分析[J].装备学院学报，2012,23(5):78-80.

[5]WayneL.Winston.Operationsresearch[M].北京：清华大学出版社，2011.

[6]李维铮，甘应爱，田丰.运筹学[M].北京：清华大学出版社，2005.

[7]傅清祥，王晓东.算法与数据结构[M].北京：电子工业出版社，1998.

[8]DreyfusSE,LawAM.TheartandtheoryofDynamicProgramming[M].AcademicPress, 1977.

[9]马仲蕃，魏权龄，赖炎连.数学规划讲义[M].北京：中国人民大学出版社，1981.

[10]俞玉森.数学规划的原理和方法[M].武汉：华中工学院出版社，1985.

[11]王晓迪.高等学校教育装备管理决策支持研究[EB/OL].[2014-07-16].http://www.cnki.net/KCMS/detail/detail.aspx?QueryID=0&CurRec=1&recid=&filename=1012518514.nh&dbname=CDFDLAST2014&dbcode=CDF

D&pr=&urlid=&yx=&v=MDkyMzJGeURtVnJySVZGMjZITGE1RnRUTnE1RWJQSVI4ZVgxTHV4WVM3RGgxVDNxV

HJXTTFGckNVUkw2ZmJ1ZG8.

[12]沈贵林.基于动态规划的物流装备更新决策方法[J].2006,29(12):24-25.

[13]杨媛媛.装备更新决策综合方法[J].2002,13(4)：51-54.

[14]陈庆华.装备运筹学[M].北京：国防工业出版社，2005.

(责任编辑杨继森)