静压下吸声覆盖层的遗传优化方法

张 冲，耿洪健

(海军工程大学 a.动力工程学院; b.训练部，武汉 430033)

吸声覆盖层是一种敷设在水下航行器表面具有吸声作用的橡胶结构，自从Alberich 消声瓦被应用以来，吸声覆盖层的机理性能、仿真优化等相关问题一直研究不断［1-2］。目前，对于吸声覆盖层的研究大都在常压条件下进行的。汤渭霖等［3］将常压下的覆盖层单元近似为黏弹性圆柱管，分析了其在声波垂直入射条件下的吸声性能。Ivansson［4］利用数值分析的方法建立了常压下的覆盖层模型，对其吸声性能进行仿真研究，并将遗传优化运用到拓宽吸声频带中。Renato Barbieri［5］、袁博［6］等利用有限元和遗传算法对吸声覆盖层的几何结构进行了优化，研究结果指出，通过遗传算法可以得到较优的结构设计参数，并分析了优化变量对几何结构的影响。

但航行器在水下工作时要受到静水压力的作用，导致覆盖层的空腔形状、材料性能等因素发生变化。胡碰［7］设计了测量橡胶在静压下的动态力学参数的方法，利用波动理论和弹性理论研究了弹性圆柱管的声学参数和材料参数之间的解析关系。陶猛［8］、邹明松等［9］基于吸声覆盖层的二维解析理论，利用有限元软件模拟了静压下吸声覆盖层的腔体单元变形，结合计算结果分析了静压对其声学性能的影响。

以上所述，或是对常压条件下的吸声覆盖层进行优化，或是对覆盖层在静水压力下的声学性能进行分析，并没有提出静压下覆盖层的优化设计。鉴于此，本文着重研究在静水压力下吸声覆盖层的模型优化问题。首先利用有限元法建立了静水压力下平面波垂直入射吸声覆盖层的分析模型，在此基础上利用遗传算法(Genetic Algorithm，GA)对覆盖层的几何结构和材料参数进行了优化，实现了平面波垂直入射时吸声覆盖层在静水压力条件下的最优化设计，对工程应用具有很好的参考价值。

1 有限元简化模型［10］

Alberich 型吸声覆盖层的研究从20 世纪50年代一直延续至今，因为它代表了覆盖层的基本结构，图1 为典型圆柱空腔吸声覆盖层及其单元近似结构图。在黏弹性体内有成正三角形排列的相互平行的圆柱空腔，把整个覆盖层看成是由多个以圆柱空腔为中心的正六棱柱体组成，由于结构对称、重复，只需要研究其中一个棱柱体中的波传播即可，每个单元可以近似看作是内部充满空气的有限厚度的黏弹性圆柱管［11］，由3 个部分组成:表面层、穿孔层、基层。假设表面层、穿孔层、基层为同一种黏弹性材料，且表面层和基层非常薄。设圆柱管外半径为a，内半径为b，厚度为L，覆盖层的背衬为刚性界面或自由界面。当声波垂直入射时，在轴向对称激励下，圆柱管中激发起各阶固有的简正波。

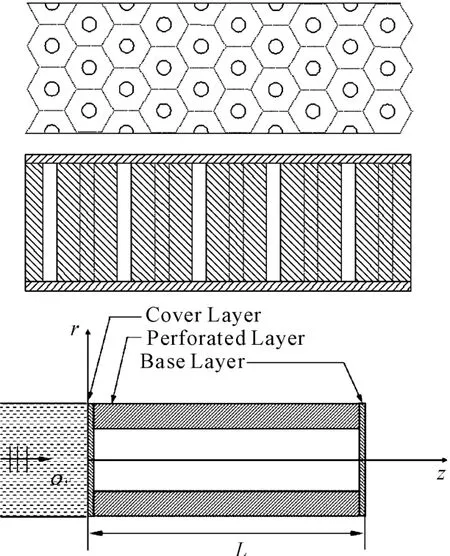
图1 吸声覆盖层及其单元的近似结构模型

线性结构以频率ω 做稳态简谐振动时，描写运动的微分方程可以写成:

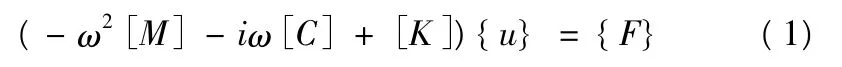
其中，［M］、［C］、［K］分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;{u}是节点的位移向量;{F} 为结构所受激励的等效节点载荷向量。

将橡胶材料的刚度矩阵［K］改写成黏弹性材料的复刚度矩阵［K～］

由于黏弹性材料的复刚度矩阵包含了阻尼损耗特性，所以在式(1)中略去阻尼项，整理得到:

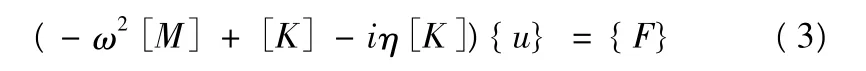
与式(1)比较，得到以刚度矩阵和损耗因子表示的阻尼矩阵

另外，在COMSOL 中通过设置声固耦合模块可以处理水介质-橡胶等声固耦合的作用，通过设置吸收边界解决无限水介质区域。

由COMSOL 计算出入射端面节点的声压和入射功率，然后计算橡胶中节点的吸收功率，按节点所占的表面积积分得到反射系数R。当背衬为硬边界时，定义吸声系数:

其中∣R ∣表示反射系数的幅值。

2 静压下吸声覆盖层的模型优化

静水压力作用于吸声覆盖层，会引起腔体的几何结构及材料参数的变化。由于以橡胶为代表的黏弹性高聚合物，其特性随着温度、压力、频率等变化而变化［12］，优化数据量会很庞大，因此，本文假设选用的橡胶基体是一种理想的材料，即动态力学参数不随频率、温度、压力等变化而发生变化，在每组优化中是定值。静压下声波垂直入射的均匀圆柱形空腔的吸声覆盖层的优化问题可从以下两方面研究。

2.1 静压下吸声覆盖层的有限元分析

吸声覆盖层在水下受到高静水压力的作用，其腔体结构必然会发生变化，在建立有限元模型时，可首先考虑在一定的压力载荷下，计算固体力学的稳态，从而得到覆盖层在静压下的变形;然后在此基础上，重新划分网格，作为吸声覆盖层的声学性能分析模型［11］。

由于本文采用的二维轴对称模型，如图2(a)，需要对模型的边界条件进行说明。三维模型的周期性边界转化为二维轴对称模型的法向量位移为0 的边界，即边界6;由于边界1 与水下航行器相连，其边界位移是固定的; 同时由于对称性，边界7、8 的径向位移为0，即只能在轴向变形;边界2、3、4、5 是自由变形的边界，用来模拟仿真覆盖层空腔内、外壁的变化。

在固体力学模块下，计算模型的稳态，从而得到覆盖层在受到静压后的变形，如图2(b)。从图中可以看出，吸声覆盖层的表面层发生弯曲变形，同时，空腔内壁发生轻微的径向变形，从而导致覆盖层空腔的半径和容积都发生变化。然后利用有限元划分网格后，在有限元模型的Z 轴方向外端面添加平面波辐射条件，使有限厚度的有限元水层代表无限厚的水介质，利用声-固耦合模块，计算吸声覆盖层的吸声系数。一般来说，空腔在静压下的变形属于几何非线性变形［10］，故求解器通过牛顿迭代运算来解决变形的非线性问题。即将载荷分解成一系列的载荷增量，使得载荷逐步达到设定的值。在每个载荷增量求解过程中，通过迭代方法求解一系列线性方程，迫使结果达到平衡收敛(在一定的容差范围内)，最终得到非线性问题的解。

图2 吸声覆盖层的二维轴对称模型

2.2 静压下吸声覆盖层遗传优化

文献［13］针对圆柱型空腔吸声覆盖层在常压下的低、高频吸声机制不同，利用多目标遗传算法对覆盖层的参数进行了优化，得到了吸声问题的Pareto 最优解集。本文基于理想材料，主要从空腔的几何结构和材料属性(包括杨氏模量、损耗因子、泊松比等)对静压下的吸声覆盖层利用遗传算法(GA)进行优化设计。

GA 是一种全局随机搜索方法，通过选择过程来实现。进行选择的原则是适应性强的个体为下一代贡献的概率大。静水压力下吸声覆盖层的GA 优化包括以下步骤:

1)建立静压下的吸声覆盖层模型，确定待优化的几何参数和材料参数;

2)设定GA 的群体大小、最大迭代次数、交叉概率、变异概率等;

3)根据初值，生成初始群体随机数组;

4)调用建立的静压模型，计算种群数组的吸声系数;

5)根据目标函数计算每一代群体中各个个体的适应度值;

6)判断当代种群个体是否满足优化终止条件;

7)若当代种群满足终止条件，结束程序;若不满足终止条件，则筛选目标函数值较优的个体;

8)对筛选的精英个体进行复制、交叉和变异，生成新的种群数组;

9)判断新生成的种群是否达到最大迭代次数;

10)如果达到最大迭代次数，退出程序; 如果未达到最大迭代次数，则将生成的新种群作为初始种群，循环第4 步骤所进行的运算。当GA 优化完成后，即可得到吸声覆盖层优化变量的最优值。计算流程如图3 所示。

图3 遗传优化的流程

3 算例分析

本文以图1 所示的圆柱型空腔的吸声覆盖层为例对其进行优化。每个单元包括水层、覆盖层(包括表面层、穿孔层、基层)、硬边界背衬(图1 中未画出)，覆盖层空腔的高度为H，表面层和基层的高度为(L-H)/2，边界为刚性边界。

由于使用的理想材料，因此本文在建立适应度函数时只考虑覆盖层的声学性能［6］，所用的适应度函数为

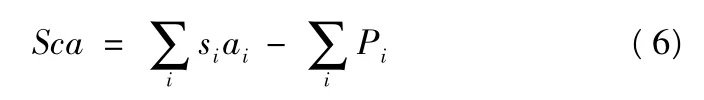
式(6)中:si表示第i 个频率点上的吸声系数;ai表示第i 个频率点的权值，较大的权值表示对该频率点的优化结果更加重视;Pi表示对第i 个频率点吸声系数的惩罚值，以促使优化结果高于某一标准。

确定待优化的参数为覆盖层外半径a，内半径b，橡胶杨氏模量E，密度ρ，泊松比ν，损耗因子δ。覆盖层高度L =50 mm，空腔高度H=44 mm，表面层和基层高度3 mm 为定值，优化频带为100 ～6 000 Hz。各优化参数初始值及上、下限如表1 所示。

表1 优化参数初始值及上下限

基于Matlab 语言编程，在载荷为P=1 MPa，种群个数为100，优化的最大迭代次数分别为20、40、60 次时，对各参数进行优化，结果如图4 所示。

图4 1 MPa 下吸声覆盖层吸声系数曲线

通过图4 的吸声系数曲线可以看出，优化后的吸声系数在500 Hz 以后明显高于初始值求得的吸声系数;而且3 条优化后的吸声系数曲线变化趋势大致相同，这初步说明优化结果属于解空间中的全局最优解。

本文还就常压下和静压下的研究结果进行了比较，在初始值和上、下限相同的情况下，分别对常压下的模型和静压(P=1 MPa)下的模型进行最大迭代次数为40 次的优化，得到的优化结果如表2 所示。

表2 优化后参数

从表2 中数据可以看出，同样优化40 代，常压下覆盖层的结构参数内、外直径是静压下的2 倍左右，而静压下的材料杨氏模量是常压下的1.67 倍。由于密度、泊松比、损耗因子上下限取值范围较小，常压下和静压下的优化结果没有出现太大差别。为了更直观的说明两者的优化的差异，本文还将常压下优化的参数带入到静压模型中，计算吸声系数，并与静压下优化的吸声系数作比较，如图5 所示。

图5 常压优化和静压优化在静压模型中的吸声系数比较

从图5 中可以看出，常压下的优化参数应用到静压模型中，计算所得吸声系数小于静压优化所得吸声系数，说明单纯的对常压下的吸声覆盖层进行优化，并将优化的参数应用到实际的水下航行器上，不一定会提高航行器的隐身性，甚至更易暴露目标。主要原因是，常压下的优化是在一个大气压下进行的，相当于水下航行器在水面漂浮的状态，而航行器的实际工作是在水下百米深处，所受的压力远远大于水面标准气压，如果把常压下的优化结果用于水下设计，其空腔结构和材料参数必然会发生很大的变化，对覆盖层的吸声性能带来影响;而静压下的优化正是考虑到航行器实际的工作压力，在此基础上进行的研究，优化的结果必然比常压下的性能要好。因此对静压下的吸声覆盖层进行优化是很有必要的。

4 结束语

本文针对静水压力下的圆柱型空腔吸声覆盖层，利用COMSOL 软件进行了建模，并与遗传算法相结合对其空腔结构和材料参数进行了优化。结果表明:

1)常压优化和静压优化相比，后者优化的参数更能在水下很好的提高吸声覆盖层的吸声系数，前者在高静水压力下会导致吸声性能发生很大的变化;而且常压和静压下的吸声覆盖层空腔结构有很大差别。

2)遗传优化可以充分考虑吸声覆盖层的低频和高频之间的耦合，针对不同的吸声频段需求，利用相应的适应度函数，设计所需性能的覆盖层。

3)由于遗传优化从全局进行搜索，可以推测，如果种群数目增加，参数选择范围更广，会得到更优的设计参数使得低频吸声性能提高，从而减少低频声呐发现水下航行器的概率，在后续学习中需对该问题进行研究。

［1］张浩，傅欣艺，尹铫，等.吸声覆盖层研究进展［J］.应用声学，2013，32(4):295-304.

［2］孟晓宇，肖国林，陈虹.国外潜艇声隐身技术现状与发展综述［J］.舰船科学技术，2011，33(11):2011.

［3］汤渭霖，何世平，范军.含圆柱形空腔吸声覆盖层的二维理论［J］.声学学报，2005，30(4):289-295.

［4］Ivansson S. Numerical modeling for design of viscoelastic coatings with favorable sound absorbing properties［J］.Nonlinear Analysis，2005，63:e1541-e1550.

［5］Renato Barbieri，Nilson Barbieri. Acoustic horns optimization using finite elements and genetic algorithm［J］.Applied Acoustics，2013，74:356-363.

［6］袁博.局域共振声学结构水下吸隔声特性研究［D］.长沙:国防科学技术大学，2013.

［7］胡碰.静水压力下声学覆盖层声学性能模块化方法研究［D］.上海:上海交通大学，2008.

［8］陶猛，卓琳凯.静水压力下吸声覆盖层的声学性能分析［J］.上海交通大学学报，2011，45(9):1340-1344.

［9］邹明松，吴文伟，余晓丽，等.静水压下声学覆盖层声阻抗研究［J］.舰船科学技术，2013，35(3):57-60.

［10］陶猛.消声瓦的吸声性能预报及降噪机理研究［D］.上海:上海交通大学，2009.

［11］Panigrahi S N，Jog C S，Munjal M L.Multi-focus design of underwater noise control linings based on finite element analysis［J］.Applied Acoustics，2008，69(12):1141-1153.

［12］黄修长，朱蓓丽，胡碰，等.静水压力下橡胶动态力学参数的声管测量方法［J］. 上海交通大学学报，2013，47(10):1503-1508.

［13］陶猛，王逛玮.基于多目标遗传算法的吸声覆盖层参数优化设计［J］. 上海交通大学学报，2013，47(8):1300-1305.