爆破震动对库存弹药的影响与对策

戴革林，周弘扬，王为奎

(空军勤务学院航空弹药系，江苏徐州 221000)

我军械仓库大都处于山区与丘陵地带，近年来，随着经济的快速发展、城市化进程的快速推进以及高铁隧道开挖等民用爆破工程的逐年增多，基于经济利益的驱使，有的民用爆破工程距离仓库很近，特别是大、中型硐室爆破、隧道掘进爆破的施工直接威胁库存弹药的质量安全，除引发军民纠纷外也给库存弹药留下大量质量不明的“定时炸弹”［1-2］。由于爆破引起的震动时间较短以及军械仓库缺少必要的爆破震动监控手段，这类受爆破震动影响后的弹药的危险性与隐蔽性极强，给库存弹药的码垛、装卸、运输等勤务处理带来极大的安全隐患。

1 爆破震动的机理

当炸药在岩石内部爆炸时，爆破冲击波与压缩波将岩石破坏，当压缩波到达一定距离后，再也不能引起岩石的破裂，只能引起岩石质点的弹性震动，这种震动以弹性波的形式向外传播，引起冲击波、压缩波与地震波。当距离大于150 倍药包半径时，压缩波变为地震波。它与天然地震一样也会引起介质内部与地面的震动，图1 表示了爆破地震波的形成与传播机理。

图1 爆破地震波的形成与传播机理

地震波具有远距离传播特性，是由若干复杂波组成，可分为体波(包括纵波与横波)与面波(包括瑞利波与勒夫波)［3-4］，可在介质内传播，也可对介质进行拉伸与压缩，引起远处地面震动与地面建筑物的破坏［5］。当然，工程中可以通过控制如爆炸震源的大小和位置以及爆心距、装药量等因素影响质点震动速度以及加速度从而可以控制爆炸震动对结构的效应。

1.1 震动速度模型分析

我国计算爆破震动安全允许速度为［6］

式中:r 为药包半径(mm); V 为地震波引起的保护对象所在地面所产生的质点震动速度(cm/s); Q 为单次爆破药量(kg);R 为爆破中心到保护物距离(m); K、α 为地质条件系数与衰减系数，数值按照《爆破安全规程》中的规定选取。

由此可以计算保护对象(楼房、库房、库存弹药)所在地面所产生的质点震动速度，质点震动速度随单次爆破药量增大而增大，随距离的增大而减小。

1.2 震动加速度模型分析

通过地震波观测数据研究表明，同时应该考虑离爆心的距离和炸药当量的影响，也就是在构造幅值包络线函数L(t)时应考虑到距离和炸药当量的影响。

关于爆炸地震波的模拟理论分析方面，曾德斌等将M.Shinozuka 等得出的双指数包络函数［7］通过改进应用于爆破地震波的模拟来反映峰值前的幅值增长规律为

式中:L0，b1，b2为给定的常数; t 为时间; t0为地震波到达时间，s;t0=R/c，c 为波速，m/s。

赵申，冯仲齐等又将L0用amax来代替，得出了包络函数新的改进形式:

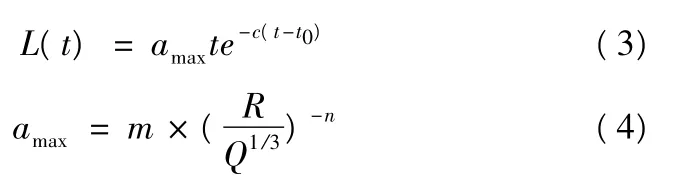
式中:amax为爆破地震波最大加速度，m/s2; 根据文献［8］中可知:常数c=10，n=2.03，m=448.53。

2 爆破震动对弹药部件影响因素分析

储存是弹药相对静态的环节，弹药包装件在重力作用下承受静压载荷作用。静压载荷主要作用于弹药外包装，一般不会对内装弹药造成直接影响。因此包装破损、弹药零部件损坏和其他质量问题的主因主要是各种形式的冲击和震动构成了弹药储运的动态力学环境。

如图2 所示:以T 为尺度的检测周期观测抽取的3 个同样的部件。部件1 由于工作环境恶劣或者突然失效造成的故障，下降极快，无法避免;部件3 由于提前更换部件造成剩余寿命浪费的问题，技术手段可以为之延长一定的寿命; 部件2 是因为长期储存中，受到震动的影响，故障发生达到各部件的CBM(Condition Based Maintenance)状态基准线时间值在部件1 和2 达到CBM 时间值之间，但之后故障发展却急剧加速，受损加剧。所以必须采取有效的措施监测弹药潜在故障发生时间，以此利用技术手段规避风险。

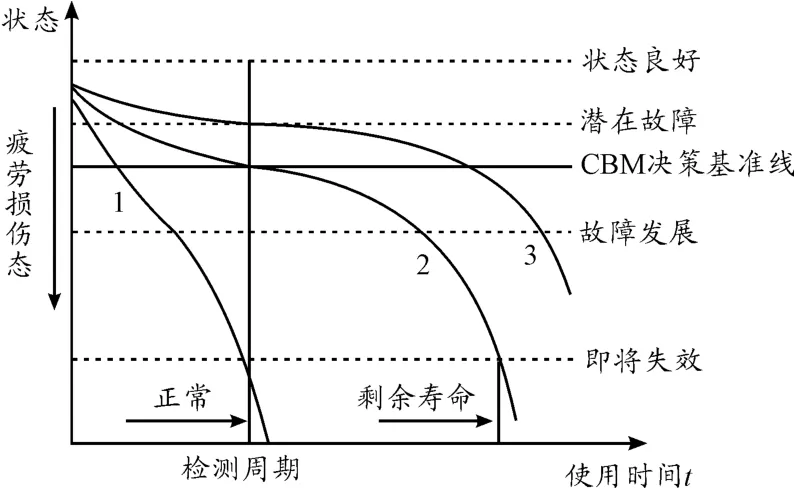
图2 固定检测周期下不同条件弹药疲劳损伤状态

在工程爆破施工中，往往就伴随着冲击和振动等动载荷作用，会在瞬间对包装件形成较大的峰值破坏，对于弹药中那些易受震动影响的部件如表1 所示影响更大。与跌落、猛烈撞击的单次震动相比，爆破工程一般长时间连续作业，震动次数多，在缺少监控手段情况下，特征不明显，很难发现与预防，与跌落、猛烈撞击的弹药相比具备更大的危险性与隐蔽性，是引发爆炸事故的隐蔽性极强的“定时炸弹”。这种动载荷既容易造成外包装箱破损，也可能导致弹药内部机构破坏或提前动作，如引信机构解除保险;零部件松动、变形和断裂;装药松动和破裂等。这些后果不仅影响弹药的正常储存，对弹药勤务的安全造成严重危害。

表1 具有震动敏感特性的弹药部件

对某一弹药来说，易损部件疲劳极限是确定的，循环次数与工程爆破次数、时间相关。因此，本研究以弹药的某一易损部件为关键部件，考虑单次爆破，震动加速度对其影响，建立弹药震动模型，分析震动对弹药影响关系。

3 数值分析震动对弹药的影响

为方便研究，本文选取文献《某型机库桩基快速成孔施工技术研究》中的炸药包为原型，在此基础上加大弹药当量，满足地震波形成条件。爆破药包［9］如图3 所示(单位:mm)。

图3 爆破药包

整个药包成柱状结构，总高度220 mm，其中上部70 mm为直径200 mm 圆柱，中部50 mm 为圆台，下部100 mm 为直径233 mm 圆柱，最下部800 mm 为药包支架，由三根角铁焊接而成，用于放置药包，形成有利炸高。其中起爆装置1 由压制的特屈儿药柱和8 号电雷管组成，隔板2 采用红松木，药型罩3 采用等壁厚的半球型(或圆锥型，未画出)的铸铁、铸铜和铸铝的金属罩，支架4 由三根角铁焊接(或铁管)焊接而成，炸药5 用20%梯恩梯和80%黑索金混合熔铸而成，外壳6 由厚2 mm 铝皮焊接而成，整个药包总质量约41.2 kg，装药总质量约30.75 kg。

模型选取使用函数式(1)、式(3)和式(4)，计算得出图4、图5、图6 是在不同距离(10 m，20 m，30 m)，相对应的时间为0.01 s，0.02 s，0.03 s 处的爆破震动时程的数值模拟结果。结果表明，弹药当量一定时，不同距离处爆破震动频率和幅值因中心距不同而不同，时间越短幅值越高，震动加速度越大，在一定时间后接近为零，对弹药部件破坏越小。

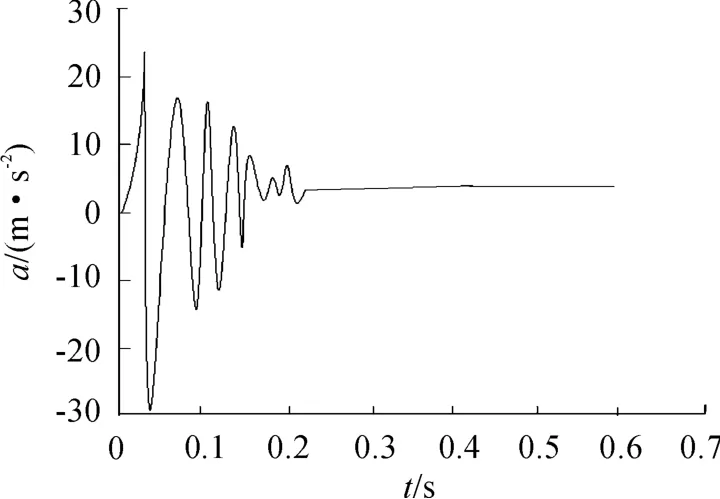
图4 爆破地震波加速度时程(t0 =0.01 s，s=10 m)

图5 爆破地震波加速度时程(t0 =0.02 s，s=20 m)

图6 爆破地震波加速度时程(t0 =0.03 s，s=30 m)

30 kg 的弹药当量，在10 m 范围内地震波的加速度峰值接近30 m/s2，而工程爆破的弹药使用量以及次数与之相比较，加速度峰值一定更高。

以某型箱装弹药为研究对象，建立了关于易损部件的三自由度弹药振动力学模型，包装箱正常情况有枕木与大地隔开，因为共振效应［10］，可以假设之间有“共振弹簧”的存在如图7 所示，为方便观察，中间镂空。在地震波加速度激励的动力作用下，弹药与之振动响应。“共振弹簧”阻尼系数主要受到包装箱减震程度、弹药整体质量等因素影响，受到的位移力取决于弹药当量与中心距。某型箱装弹药位置与爆破中心距越远且弹药包装箱保护能力越好，共振程度越低。因此，工程爆破产生的震动必须受到重视，对弹药保护也要足够重视，箱体要有一定的抗震性。

图7 箱装弹药震动与共振弹簧关系假想图

4 解决措施

1)加强军地双方沟通与协调

民用爆破的管理与批准权限隶属地方公安系统的治安管理局(科)，每次实施爆破前必须报请治安管理局(科)批准［11-13］，为准确掌握地方爆破工程实施的规模、时间与地点，必须加强与地方公安部门的协调与沟通，军地双方及时通报爆破工程作业实施信息，必要时进行爆破震动监测，及时采集爆破震动的关键数据，分析库存弹药受爆破震动的影响情况。

2)对爆破震动进行有效控制

根据上述爆破震动质点速度以及加速度公式可知，爆破震动质点速度与单次爆破药量成正比，与距离成反比，因此必须控制单次起爆药量，禁止大型峒室爆破与库区附近的隧道爆破，确实需要进行隧道爆破的，建议承包公司该标段采取盾构施工技术或对爆破震动进行有效控制，主要控制技术包括:降低单次起爆药量、多次起爆、采用低威力、低爆速炸药，除此之外，采取毫秒微差爆破技术，实践证明，毫秒微差爆破与齐发爆破相比，降震效果非常明显，间隔时间大于100ms 时平均降低震动50%左右［14］，分段越多，降震效果越好，采取毫秒微差爆破技术是对爆破震动进行有效控制的关键技术措施。

3)购置便携震动监测仪

为控制爆破，减少爆破破坏效应以及对爆破工程方案进行性能评估等用途，目前国内对爆破效应采取mini-series 便携震动监测仪进行监控［15］，该仪器体积小巧，自备电池，放置于监控场所自动记录震动波形，无需人为参与值班，自动记录，发现异常情况或定期对记录波形结果进行分析，分析震动波形前震段、主震段与尾震段，重点分析震动幅值、震动发生的时间、持续时间等关键技术数据，有利于与民用爆破公司一起改进爆破技术方案。

4)改进弹药包装箱

为了提高弹药防震能力，除在弹药码垛时底部采用防震垫木、有机减震材料等措施外，改进弹药包装箱的防震能力是一个有效方法，具备防震能力的弹药包装箱也称为缓冲包装箱，可以采取全面缓冲、部分缓冲与悬浮缓冲3 种方式解决弹药防震问题，其中部分缓冲是在弹药包装箱拐角或局部地方使用缓冲材料衬垫，不仅能产生良好的防震效果，与全面缓冲和悬浮缓冲相比大大降低材料成本，是应用最广泛的缓冲包装措施，可以很好解决爆破震动对库存弹药的影响。

5 结束语

去年某部后方军械仓库在进行弹药勤务作业时发生爆炸，给库存弹药勤务处理安全带来严重影响，分析可能影响库存弹药安全因素成为重要研究课题，特别是隐蔽性强的质量不明弹药是造成爆炸事故的主要因素，本文基于近年城市化进程的不断加快以及高铁隧道工程的不断增多，地方民用爆破对后方军械仓库库存弹药安全构成严重威胁的实际情况，提出了受爆破振动影响后的质量不明弹药是一种被忽视的危险库存弹药，给出了爆破震动对库存弹药机械结构的影响以及这种危险弹药出现的原因，给出了几种具体的解决措施，可以及时发现与解决这类危险弹药的隐蔽性问题，对于库存弹药的防爆安全具有一定的参考价值。

［1］叶平.军械仓库安全技术［M］.北京:海潮出版社，2007.

［2］于亚伦.工程爆破理论与技术［M］.北京:冶金工业出版社，2007.

［3］Fernando D A，Enrique G F，Marta D M，et al.Consequence analysis by means of characteristic curves to determine the damage to humans from the detonation of explosive substances on a function of TNT equivalence［J］. Journal of Loss Prevention in the Process Industries，2008，20(1):74-81.

［4］吴贤振，喻圆圆，刘建伟，等.不同方向爆破振动信号的分形特征［J］.工程爆破，2014，20(4): 6-8.

［5］仲伟君，李德胜，崔亮.一种制导弹药电子部件可靠性预计方法［J］.装备环境工程，2014，11(2): 103-105.

［6］FAN P X，WANG M Y，FENG S F，et al. Analysis of dynamic response of deep-buried circular tunnel to explosion seismic wave［J］. Chinese Journal of rock mechanics and engineering，2013，32(4):672-677.

［7］曾德斌，林大超，白春华，等.爆炸地震加速度幅值的包络函数模型［J］.工程爆破，2001，7(3):1-4.

［8］赵申，冯仲齐.模拟爆炸地震波及其对框架结构的影响［J］.陕西理工学院学报: 自然科学版，2010，26(4):43-46.

［9］周弘扬，王为奎，戴革林.某型机库桩基快速成孔施工技术研究［J］.空军勤务学院学报，2014，25(6):46-47.

［10］李海广，安振涛，任永强.弹药公路运输振动响应模型及影响因素分析［J］.计算机仿真，2013，30(12):1-4.

［11］洪亮，胡小国，崔旭涛.海军导弹环境适应性试验条件建设方案研究［J］.装备环境工程，2012，9(6):97-103.