飞机战伤抢修性评价模型研究

张均勇，赵 磊，李武奇，李曙林

(1.空军工程大学航空航天工程学院，西安 710038; 2.中国人民解放军93115 部队，沈阳 110031;3.沈阳军区空军装备部外场处，沈阳 110015)

面对未来战场的需要，要提高飞机的作战生存力，就必须进行以飞机生存力为中心的飞机战伤抢修性设计［1］，而抢修性设计的优劣，势必要建立抢修性评价体系且采用合理的评价方法进行抢修性评价才能得出结论［2-8］。根据评价结果进行全方位的权衡，以保持和恢复飞机作战环境所需的作战能力。对飞机进行战伤抢修性评价，有利于各部门、各系统相互配合协调，资源共享，以求得飞机寿命周期的最佳效能—费用比，从整体上提高飞机的战伤抢修性。由此可见，飞机战伤抢修性评价是关键的、非常有必要的，并且迫切需要建立一整套科学、合理的抢修性评价模型，以提高飞机的战伤抢修性。

1 定性模型(qualitative model)

由于飞机战伤抢修性本身具有的特殊性、复杂性和不确定性，要直接定量评价抢修性有很大难度，因此，可以考虑利用定性模型进行抢修性评价。本研究所建立的抢修性定性模型:是指依据飞机抢修性定性要求，将表示系统影响因素的定性变量细化，分解成可以直接定量或定性表达的形式，用以描述飞机抢修性问题与定性变量之间的依赖关系，而定性变量的值可以基于专家意见、历史数据、经验知识来定性确定，再结合层次分析法、模糊综合评价法、灰色关联度评价法等评价方法，从而把抢修性定性问题定量化的一种模型。

1.1 定性模型的建立

飞机战伤抢修性定性模型

式中y1表示抢修性影响因素的定性变量。

如果定性变量yi还有它们各自的子影响因素，其组成因素的表示式分别为:

式中xij分别表示yi的各个子影响因素变量。

将式(2)代入式(1)，即可得抢修性定性模型的影响因素变量表达式。

该定性模型利用抢修性影响因素变量与抢修性间的定性关系，去揭示飞机战伤抢修或抢修性的规律，也可得到抢修性方案或抢修预案的优劣趋势。

1.2 定性模型的应用步骤

该定性模型的应用步骤如下:

1)根据飞机抢修性的定性要求，提取抢修性定性影响因素，建立定性影响因素结构图;

2)按照定性影响因素结构图，构建定性模型表达式;

3)利用相关评价方法(如层次分析法)进行抢修性评价，将定性问题定量化;

4)依据评价结果，可得出方案优劣趋势。

2 定量模型(quantitative model)

抢修性作为飞机装备的一种新的特性，就应当有优劣高低之分。例如，如果战场损伤的飞机在战场上能被及时抢修好投入下一次战斗任务，则认为其抢修性好，否则就认为抢修性不好。当然，具体到一战场损伤飞机在战场上能不能修好，与多方面的因素有关，例如飞机的结构、损伤的部位、损伤的程度等。由于战争的特殊性，并非所有损伤都能修复(例如因为损伤程度、时间、备件等的限制)，这种特性甚至只能用一种可能性的高低来表示［9-12］。因此，飞机战伤抢修性实际上是飞机系统在遭受战场损伤时，所表现出来的能被抢修到满足任务要求状态的能力，这种能力的定量描述是一个难题，到目前为止，尚未见到完整的评价飞机抢修性的定量模型，因此有必要对飞机抢修性定量问题进行深入研究。本文参照可靠性和维修性分析方法，尝试构建了2 种抢修性定量模型，以解决抢修性定量描述的难题。

2.1 可抢修度定量模型

由于抢修性主要反映在抢修时间上，而抢修时间又是个由很多因素影响的随机变量。因此，可抢修度模型可根据抢修时间的概率分布为基础进行建立，实现对抢修性能参数的合理度量，从而有效解决抢修性的量化难题。

2.1.1 抢修性函数

1)可抢修度Q(t)

抢修性的概率表示为可抢修度，记为Q(t)，即在战场上规定的时间内，使损伤的飞机装备经抢修能够迅速地恢复到其完成某种任务所需功能的概率，可表示为

式中T 表示在一定的作战环境下使飞机装备恢复基本功能的时间，t 表示规定的抢修容许时间。

Q(t)也可表示为

式中:N 表示需要抢修损伤的装备数;N(t)表示在时间t 内通过抢修恢复基本功能的装备数。

不可抢修包括两种情况:一是损伤装备没有抢修意义;二是可进行抢修，但因种种原因(主要有:①备件不能按时送到，不能如期实现抢修目标;②不抢修某个部件并不影响某种任务所需;③抢修技术人员的问题。)，从而失去抢修意义。对此不可抢修的度量可用不可抢修度来描述。不可抢修度，是指在战场上规定的时间内，损伤的飞机装备不能够迅速地恢复到其完成某种任务所需功能的概率，可表示为

Q(t)也可表示为

因为在某时刻，损伤的装备只能处于可抢修或不可抢修两种状态之一，因此有

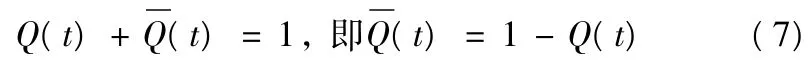
3)抢修密度函数q(t)

可抢修度Q(t)是时间内完成抢修任务的概率，那么，其概率密度函数可表示为

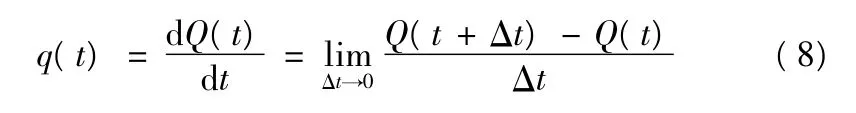
4)抢修率μ(t)

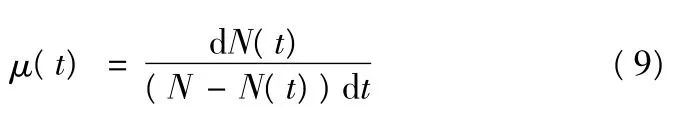
抢修率指在战场上规定的条件下和规定的时间内，在t时刻未恢复基本功能的装备在时刻dt 后单位时间内恢复基本功能的概率，即单位时间内飞机系统装备的瞬态修复概率。可表示为式中:N 表示需要抢修损伤的装备数;N(t)表示在t 时间内通过抢修恢复基本功能的装备数; dN(t)表示t 时刻后dt 时间内通过抢修恢复基本功能的装备数。

5)抢修率、抢修密度函数与可抢修度或不可抢修度函数的关系

2.1.2 抢修性参数

抢修性参数是度量抢修性的尺度，因此它们必须能够进行统计和计算。从抢修性函数模型可以看出，抢修时间参数是飞机系统抢修性的重要参数，弄清抢修时间的概率分布是研究抢修性定量化的基础。对数正态分布适用于由修理频率和持续时间都互不等的若干项工作组成的维修工作项目。根据战场抢修时间的统计规律性以及文献［13 -14］表明，战场抢修时间通常服从对数正态分布。

飞机系统的平均抢修时间是指在战场上使损伤装备恢复基本功能所需实际时间(包括损伤评估时间和损伤修复时间)的平均值，或抢修时间的数学期望，即

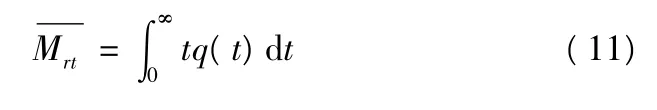
若按统计定义，平均抢修时间也可表示为抢修时间总和与抢修次数之比，即

飞机系统的最大抢修时间是指飞机系统装备损伤后使其恢复到足以完成当前任务或基本功能的最大可能时间。确切地说，应当是给定可抢修度百分比的恢复时间，通常给定可抢修度是95%(或90%)。最大抢修时间通常是平均恢复时间的2 ～3 倍，具体比值取决于抢修时间的分布和方差及规定的百分比。在实际应用中，某个损伤的最大抢修时间不能大于当前作战任务容许的最大抢修时间，否则，抢修便没有实际意义。

3)恢复功能用的任务时间Mmrt

恢复功能用的任务时间是与飞机系统作战任务有关的抢修性参数。MTTRF 度量方法为:在规定的任务剖面内，装备致命性故障的总修复时间与致命性故障总数之比。

2.1.3 可抢修度模型的应用步骤

可抢修度模型的应用步骤通常如下:

1)根据给定的抢修时间数据和想定完成的抢修任务，按照上述抢修性参数模型，计算出相应的抢修性时间参数;

2)根据1)中计算出的抢修性时间参数，按照上述抢修性函数，便可求得相应的可抢修度等的量值。

2.2 抢修效能定量模型

2.2.1 基本假设

飞机战伤抢修效能是指战场上损伤飞机装备在规定的时间内和规定的条件下经过抢修，能恢复某一满足规定任务要求的基本功能或更多功能的能力或概率。为了建立抢修效能的数学模型，先做如下假设:

1)系统的全部功能具有有限个状态，且任一时刻系统只能且必定处于其中某一种状态。

2)系统可以担任有限种战斗任务(自救也可以认为是一种任务)，系统全部可能的状态中必定有若干种状态能满足任务要求。

3)评估人员做出的评估结论是正确的，不会发生错误。如果评估人员确定战斗损伤飞机装备在给定的时间内不能修复，则对该装备不予抢修。

4)维修人员总是尽力抢修，在可能的情况下恢复尽可能多的功能。

5)战场抢修的要求是将损伤飞机装备恢复到满足任务要求的状态之一，而实际抢修时飞机装备在给定时间内能否恢复到某一状态是随机的，其概率为时间的函数。

2.2.2 抢修效能模型的建立

假设系统具有n 种状态，其状态空间用S 表示，则

式中si表示系统处于第i 种状态(i=1，2，…，n)。

再设系统有L 种可能的任务，其状态空间记为M，则

式中ml表示第l 种任务(l=1，2，…，L)。

根据任务要求分析可知，只要系统具备基本功能就能完成给定任务，而系统所有状态中包含基本功能的状态可以有多种，今设有nl(≤n)种系统状态可以完成任务ml，其中有且只有一种状态所包含的功能恰为任务ml所要求的基本功能，因此完成该任务的系统状态空间为Sl= { sk1，sk2，…，sknl}。

任务所对应的系统状态空间是系统全状态空间的一个子集，记为Sl∈S。同时也可以得出不能完成该任务的系统状态空间就是S 与Sl的余集，记为S'l。

设系统在时刻t =0 时处于状态sj(∈S'l)，经过战场抢修到t 时刻时处于状态Skv(∈S'l)的概率为Pikv。由于系统只能处于一种状态，因此，对于任务ml，飞机装备系统由损伤状态Sj经时间t 后处于满足任务需要的系统状态的概率为

由于损伤后系统可能处于n -nl种状态，综合考虑可靠性、操作人员失误及敌方行动等因素造成的损伤后，系统在损伤后处于状态sj的概率为Dj，由于损伤必定处于某一状态，则

系统处于状态空间S'i，经抢修后在规定时间t 后处于状态空间Sl的概率Rl可用全概率公式计算

Rl正是飞机装备通过战场抢修完成任务ml的概率或能力，称之为抢修效能。

如果已知飞机装备系统的全部抢修转移矩阵P

式中Pij表示抢修前处于状态i，抢修后处于状态j 的概率。

对给定的任务ml，则有任务矩阵MS

其中

对应的损伤矩阵D 为

其中

因此，任务ml所对应的抢修效能Rl

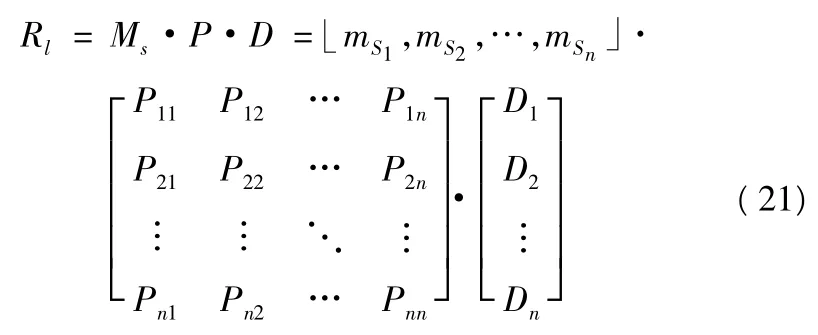
由式(21)可以计算出任一给定任务所对应的抢修效能。

2.2.3 系统总的平均抢修效能模型

上面针对的是给定战斗任务的抢修效能计算模型，而一个系统往往可以承担多种不同的任务，有的系统功能虽然相近，但承担的任务却有明显差异。因此，可以根据执行任务的频率高低来确定系统总的平均抢修效能。

设执行第l 项任务的频率为fl，则系统总的平均抢修效能为

当然如果从不同的角度来考虑，还可建立其他的计算系统总的平均抢修效能模型。例如，在实际使用装备时，执行不同的任务往往对整个战斗的贡献是不一样的，由于战场损伤后经抢修只能降额使用，虽然也能完成某一任务，但其任务的重要程度对指挥员而言则有很大的不同。因此如果考虑不同任务的重要程度，则总的平均抢修效能模型如下:

设第l 项任务的重要程度为wl，则系统总的平均抢修效能则为

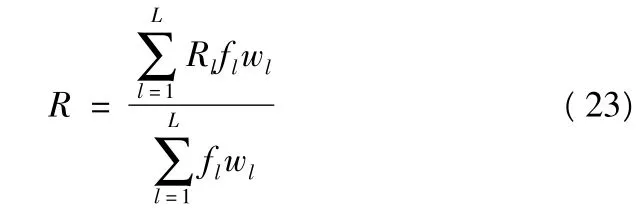
2.2.4 抢修效能模型的应用步骤

1)确定系统状态空间

本模型中有3 个矩阵，即任务、战场损伤和抢修状态转移等3 个矩阵。为确定这些矩阵，首先是应当在分析系统功能的基础之上确定系统全部的状态空间，应当将系统状态划分到一个合适的程度。划分太粗造成一个状态内包含的子状态太多，无法确定状态转移矩阵;太细则状态空间太大，数据收集过细、计算过分繁琐造成工作量太大甚至无法评价。一般应根据飞机装备所承担任务的程度及评价人员所能观察到的状态情况来进行系统状态划分，只有系统状态空间确定了，满足给定任务要求的状态空间就好确定了。

2)确定系统状态转移矩阵

确定了系统状态空间后，可以根据经验统计数据，或者是抢修试验数据，确定出每一种状态经规定的抢修程度和时间后，修复到其他状态的概率或频率。如果战场损伤评价人员的水平较高，甚至可以用评价人员的评价结果来获得这种转移概率。因为实际抢修时，抢修与否及抢修的程度都是按评价人员的评价结果来进行的。虽然这与装备本身的实际情况会有些差距，但与实际工作却相差无几。

3)战场损伤状态矩阵的确定

战场损伤状态矩阵就是战场损伤状态的分布情况，应当根据装备的可靠性水平、战场实际损伤统计数据等来确定。目前国外有许多战斗损伤模拟研究、实弹射击实验等都是为了获得这个方面的数据而进行的工作。

4)抢修时间的确定

抢修时间的长短应根据飞机装备的具体使用情况规定一个典型的抢修时间，根据国外经验可以规定在第一线是2 h，在直接支援级为24 h。

3 结束语

飞机战伤抢修性关系到飞机在未来战争的可用性。抢修性评价是战时飞机战场抢修的关键之一，也是和平时期面向战争需求对飞机抢修性进行的综合评价，根据评价结果，可对在研机型的抢修性系统方案进行筛选和改进，也可对在役机型的抢修性进行改进或改造设计，也可对战伤评估和抢修预案的最终决策起积极作用，还可用于评估飞机潜在的作战能力或战斗力增加效果，这就能够争取时间对不适合未来战场要求的飞机采取相应改革措施，夺取未来战争的主动权。

本研究从定性和定量两个角度全面建立了飞机战伤抢修性评价模型，解决了抢修性评价模型难以构建的问题，为抢修性评价提供了理论支持。评价者可根据自身需求，将抢修性作为评价主体，以抢修性相对应的属性为评价指标，选取相应的评价模型对其进行综合评价，提取其本质属性，明确其价值，加以度量，为管理层、研究层和决策层提供提高飞机战伤抢修性的建议。

［1］黄刚强，韩青山.雷达装备战斗恢复力设计初探［J］.军械工程学院学报，1993(5):1-4.

［2］曹原，杜晓明，贾希胜.基于PDA 的装备战场损伤评估［J］.兵工自动化，2006，25(1):7-8.

［3］朱小东，张森林.战斗恢复力定量评估模型初探［J］.军械工程学院学报，1995(2):29-34.

［4］董原生，苏冬寒，罗九林，等.装甲装备抢修性评价指标［J］.四川兵工学报，2008(6):13-15.

［5］侯满义，李曙林. 一种军用飞机战伤抢修性评价体系［J］.航空维修与工程，2006(2):27-29.

［6］侯满义，李曙林，李寿安.基于灰色关联层次分析的飞机战伤抢修性评价［J］.电光与控制，2006(6):68-71.

［7］闾晨光，浦金云，侯跃.基于综合抢修性能的舰艇系统评估模型研究［J］.中国修船，2006(S1):55-57.

［8］王志成，王润生.战场损伤快速评估系统数据研究［J］.军械工程学院学报，2002(3):33-37.

［9］Dennis H.Kovatch.Modelling aircraft combat damage repair［C］//Proceedings Annual R＆M Symposium. USA: New York，1984:25-28.

［10］Jeffery W.Hess.Aircraft battle damage repair［C］//Aerospace America.USA:New York，1992:5-9.

［11］Stalcup B J.The need for combat resilience［C］//Proceedings Annual R＆M Symposium.USA:New York，1986:489-493.

［12］Stalcup B J.Airland battle 2001 -design for combat resilience［C］//Proceedings Annual Reliability and Maintainability Symposium.USA:New York，1988:14-18.

［13］张建华，焦良，姚武文，等.飞机战伤抢修工程学［M］.北京:航空工业出版社，2001.

［14］李建平，石全，甘茂治.装备战场抢修理论与应用［M］.北京:兵器工业出版社，2001.