复杂装备系统可靠度和冗余度分配优化分析

任 鑫，谭新建，王辉立，张 凯，杨翊方

(1.国防大学研究生院，北京 100091; 2.海军医学研究所，上海 200433)

复杂装备系统的可靠度依赖于各个子系统和各个模块的可靠度，提高子系统和各模块的可靠度将引起系统的总造价增加，并且这种依赖关系不呈线性关系。在一定的可靠度下，如果增加系统模块的冗余数将造成系统造价的大幅提升，但由于成本造价及先天等条件的限制，整个系统可靠度很难仅仅通过提高单个模块的可靠度来实现，所以将系统可靠度和冗余度进行最优化分配尤其重要，若提高系统可靠度指标可以采取两种方式加以实现，一是提高系统模块的可靠度指标，二是增设系统模块冗余数。提高子系统可靠度指标和增设冗余模块，均是系统设计中需要统筹考虑的问题，且通常子系统最优冗余个数与其可靠度指标密切相关。所以系统模块的可靠度指标和子系统冗余数应同时进行优化，以便在满足规定约束范围内使整个装备系统的可靠度达到最优［1］，即要求系统设计者设定冗余数的同时确定每个模块的可靠度，实现系统可靠度指标和系统模块冗余数一体化最优设计。本研究通过研究解决复杂装备系统可靠度和冗余度分配最优化问题，为完善复杂装备系统可靠性和经济性优化配置提供技术支持。

1 遗传算法理论

遗传算法(Genetic Algorithm)是一种采取模拟自然进化过程来进行最优解搜索的计算方法，主要通过模拟达尔文生物进化论中的自然选择和孟德尔遗传学机理中的生物进化过程建立相关分析模型。遗传算法的主要特点就是其不需利用任何相关先验知识作为基础，便可对系统参数采取编码操作，通过各种不同路线实现平行的搜索，这样可保证能在诸多局部较优解中找到全局最优解，而不会使计算落入局部较优的陷阱，遗传算法是一种实现全局最优化的分析方法。遗传算法不局限和依赖于任何相关问题的具体领域，其被广泛地应用于不同学科，并可为复杂装备系统提供一种求解最优化问题分析框架［2］。遗传算法理论的分析流程如图1所示。

图1 遗传算法分析流程

2 模型建立及求解过程

2.1 模型建立

大型复杂装备系统通常由串联系统和并联系统混合组成，比如某复杂装备系统中拥有N 个子系统，并且在这N 个子系统中每个子系统拥有M 个并联模块，共同组合成N ×M串并联系统。其结构示意图如图2 所示。

一般情况下，提高系统的可靠度可以通过提高各子系统的可靠度和在系统中增加冗余结构的方法来实现，采用这2种方法，既提高了复杂装备系统的可靠度也同时增加了系统的容量、规模和投资等。

图2 串—并联系统结构框图

所以，对系统可靠度进行优化设计，应是在符合投资、质量和结构等基本条件下，有效提高系统的可靠度，其数学模型如下。

同时当可靠度符合一定的要求时，为取得最大的经济效益和空间效益，需要尽可能的减少投资和所占空间，其数学模型如下:

如果某复杂装备系统拥有N 个子系统，系统设计者基于每个子系统可采取多种设计方法来实现系统的可靠性要求［3］。此问题可以通过建立如下非线性整数规划进行描述:

其中:θ 是参数向量，待优化;αi(i=1，2，…，N)是各个子系统可以进行选用的设计; mi(i=1，2，…，N)是各个子系统同样的冗余单元数; μi是各个子系统的冗余单元上限; βi各个子系统的可选设计的上限;R(m，α)是系统可靠度，其具有冗余单元m 及可选设计α; C(m，α)是系统费用函数，系统具有冗余单元m 及可选设计α，且C 是关于复杂系统费用的总约束;W 是关于复杂系统权重的总约束。

对于各个子系统，具有如下计算公式

2.2 遗传算法求解过程

所用的遗传算法求解过程如下［4］:

1)参数向量θ=［m1，α1，m2，α2，…，mN，αN］T的所有分

3 应用案例

以某复杂装备系统为例，对其进行系统可靠度和冗余度的分配优化分析，此复杂装备系统结构框图如图3 所示。

图3 某复杂装备系统结构

对复杂装备系统进行可靠度和冗余度分配优化设计需要作以下3 个基本假设［5］: ①此复杂装备系统中的冗余类型是主动冗余;②此复杂装备系统中每个子系统互为独立，并且损坏后不能维修; ③此复杂装备系统中每个子系统只有工作和故障有2 种状态。所以此复杂装备系统的优化设计问题可归结为:α1，α2，…，αn为复杂装备系统的最优可选设计子系统，m1，m2，…，mn为复杂装备系统的子系统的冗余数，通过匹配优化，以在符合复杂装备系统的总造价和总权重条件下使得系统的可靠度R 值达到最大。复杂装备系统为串联系统和并联系统混合组成，包含子系统各冗余单元和可选设计，适合于如下的系统可靠性分析模型，即

式中:μi=2; βi=3。

其中，各子系统可靠度Ri大小在0 ～1 范围之间，而系统的冗余数mi(i=1，2，…，N)为整数。所以，以上复杂装备系统的优化设计问题在本质上属于离散变量和连续变量混合存在的非线性规划问题［6］。

某复杂装备系统具有6 个子系统，其中每个子系统具有3 种不同的可选设计，因空间和造价限制，其各个子系统冗余数值不超过2，复杂装备系统各个子系统冗余单元和可选设计数据如表1 所示。

表1 某系统冗余子系统和可选设计数据

根据遗传算法的求解过程编写Matlab 程序来进行求解，计算得到在进化250 代过程中的每一代最优个体和对应的系统适应度。通过不断运行函数，发现运算函数寻优非常稳定，每次计算分析均基本能得到以下的最优解:

且此最优解对应的可选设计和冗余度分配如表2 所示。

表2 最优解对应的可选设计和冗余度分配表

此时对应的系统可靠度:R(θ*)=0.999 12×0.998 42×0.999 6 ×0.999 7 =0.994 3，如图4 所示。

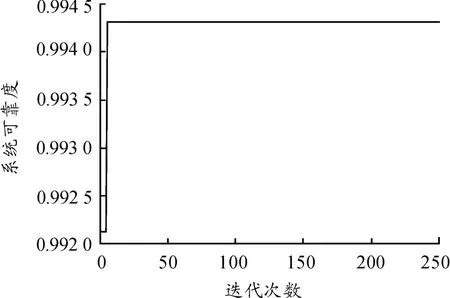
图4 系统可靠度随迭代次数的变化曲线

图4显示了系统的可靠度随迭代次数的变化曲线，由此图可以看出遗传算法在进化了10 代左右以后基本趋于稳定了，则此时已经求出了最优解。

4 结束语

复杂装备系统系统冗余多，设备造价昂贵，需要对系统可靠度和冗余度进行分配优化设计，使得在资源相对有限的情况下，实现系统各单元可靠度与冗余度的最优化配置，从而使得系统可靠度达到最大。本研究通过分析复杂装备系统的串—并联混合系统，基于遗传算法对非线性连续变量和离散变量进行混合求解，解决了复杂装备系统可靠度和冗余度分配最优化问题，为相关部门系统的优化设计提供了有力的技术支撑和决策支持。

［1］孟宪云.并—串联系统可靠度与冗余度最优化的一种算法［J］.燕山大学学报，1999，23(4):318-319.

［2］Deng J L.Control problems of grey systems［J］.System ＆Control Letters，1982，1(5):288 -294.

［3］孟宪云.多约束下的串、并联混合系统可靠度与冗余度的优化判定模型及算法［J］.经济数学，2002，19(3):91-94.

［4］殷志锋，葛新锋.基于指数积的冗余度机器人运动学求解算法［J］.制造业自动化，2013，35(1):4-8.

［5］吴霜，卫志农，孙国强，等. 考虑量测冗余度的多阶段PMU 优化配置［J］. 河海大学学报，2013，41(2): 184-188.

［6］姜勇，苑春艳.双箱结合梁桥结构冗余度评估［J］.世界桥梁，2013，41(3):66-71.