基于粒子群优化的灰色系统对一体化保障设备使用工作量的预测

单志伟，钱 潜，刘福胜

(装甲兵工程学院技术保障工程系，北京 100072)

随着我军信息化建设的不断推进，我军的基本作战形式也顺应时代要求发生变化，未来我军的基本作战形式将主要以一体化联合作战为主。一体化联合作战体现的是诸军兵种联合作战力量在联合作战指挥机构的统一指挥下，依托统一的信息共享平台，实施快速、精确、高效的联合作战行动［1］。保障作为作战的物质基础，在一体化联合作战背景下，必然要求保障也得一体化，显然，当前基于型号和基于单一兵种装备的保障体制已经完全不能适应未来战场的需要。实施一体化联合作战，必然要求作战部队装备保障实现一体化。所谓一体化装备保障［2］，就是要最大限度地实现各种装备体系所属保障设备的综合集成、快速流动和优化配置。显然，保障设备数量的确定成为一体化保障的关键问题。

目前，针对保障设备数量的配置方法有利用率法［3］、相似系统法、排队论法［4］等。利用率法的中心思想是按照一定的利用率配备保障设备的数量，考虑因素比较单一，适合确定单一型号装备的保障设备数量;相似系统法是选择现有装备的保障设备配置情况作为基准比较系统，配备保障设备的数量，这种方法主观性太强，面对一体化保障的装备型号多样化的情况，缺乏科学性; 排队论法针对的是装备出现故障后保障设备的配置问题，针对范围比较窄，无法满足一体化保障面向全系统、全寿命的要求。在此认为，一体化保障设备数量的规划配置，可以通过分析所有装备使用保障设备的总工作量与单一保障设备能够提供的使用工作量情况，确定一体化保障设备的数量。因此，确定一体化保障设备的使用工作量是确定保障设备数量的基础，为了确保最终保障设备数量配置的合理，必须保证保障设备使用工作量的科学性。

灰色系统指信息不完全的系统，即系统因素不完全明确、各因素间关系不完全清楚和系统结构不完全清楚，属于非线性的系统［5-8］。一体化保障系统涉及的范围广，需要考虑的各方面因素较多，系统各因素之间的相互关系、结构也比较复杂，这些特性均与灰色系统的特点相契合。所以，本文将一体化保障系统当成一个灰色系统来进行保障设备使用工作量的预测。然而，灰色系统预测存在精度不高的问题，因此，为了提高预测精度，我们采用灰色系统与粒子群优化相结合的方法，保证预测结果的精确性，为之后确定保障设备的数量奠定基础，有助于使保障设备的数量配置相比之前更科学、更具有经济效益。

1 一体化保障设备使用工作量的灰色系统模型

1.1 传统灰色系统模型

传统灰色模型［9］GM(1，1)的关键是构造时间序列，在本文中，时间序列就是一体化保障设备在相同时间间隔下的使用工作量序列。然后对该时间序列进行一系列的数据处理后，生成GM(1，1)微分方程，再求解微分方程中的参数，得到最终的预测模型，下面，具体说明传统GM(1，1)的建模过程:

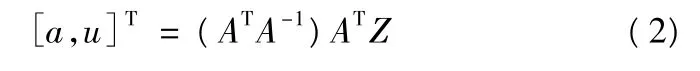
则模型的预测结果为

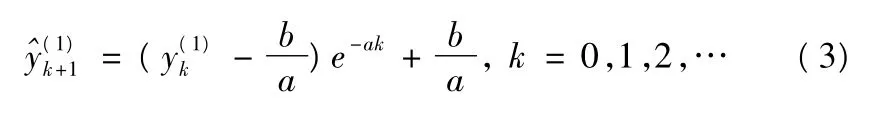
6)对式(1)～式(3)进行一阶累减还原计算(1 - IAGO)，得到y(0)的灰色预测模型:

1.2 改进的GM (1，1)模型

由式(1)～式(4)知，背景值的构造影响着GM(1，1)模型的拟合及预测精度和参数a、b 和c 的选取，因此，提高模型拟合及预测精度的关键在于求出合理的参数解以及避免形成背景值。由式(1)，则预测结果为

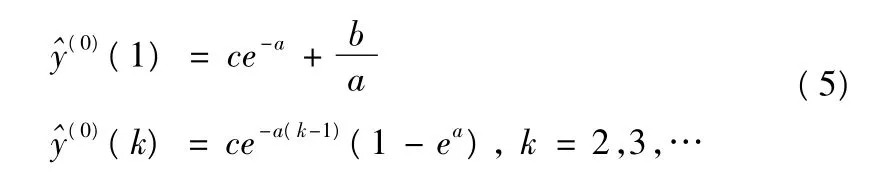
采用有全局寻优功能的粒子群算法直接求取参数a、b和c，提高模型的拟合和预测精度。

2 粒子群算法(PSO)

2.1 粒子群算法的内涵

粒子群优化算法(Particle Swarm Optimization，PSO)是由E-berhart 博士与Kennedy 博士通过对鸟群和鱼群运动行为研究而受到启发发明的一种新的全局优化进化算法［10］。该算法是想象在一个D 维的搜索空间中有n 个点，每个点都表示一个潜在的优化解，称之为“粒子”，每个粒子以一定的速度在空间内飞行，并通过自身和同伴的经验不断调整速度，粒子没经过一个位置，都会由一个目标函数来确定当前的适应值，这样，在粒子不断的飞行中，适应度值也在不断的更新，根据目标需求，可以确定最优的解。因此，采用粒子群算法直接求取参数a、b 和c，有助于找到最优解，提高模型的拟合和预测精度。

第i 个粒子的位置用向量Zi=(zi1，zi2，…，zid)，i =1，2，…，n 表示，飞行速度用向量Vi=(vi1，vi2，…，vid)，i=1，2，…，n 表示;当前单个粒子搜索到的最好位置(个体极值pBest)用向量Pi=(pi1，pi2，…，pid)，i=1，2，…，n 表示;当前整个粒子群搜索到的最优位置(全局极值gBest)用向量Pg=(pg1，pg2，…，pgd)，i=1，2，…，n 表示。所有粒子i 速度和位置的更新采用下面的公式:

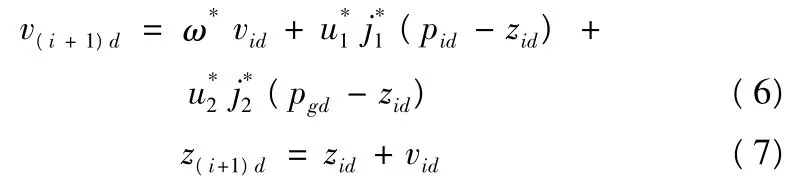
其中，u1和u2称为学习因子，一般情况下，u1=u2=2.0，j1，j2是(0，1)之间的随机数，ω 是取值在(0.1，0.9)的加权系数。粒子经过学习，不断更新自身的状态，最终到达解最优解所处的空间位置，即全局最优解gBest。为了保证能够得出最优解，在更新迭代过程中，将粒子在每一维的最大速率和坐标都限制在一定范围内。同时，为了避免粒子在全局最优解附近来回“盘旋”的问题，对速度更新迭代公式进行以下改进，让公式中的加权因子ω 随着更新迭代的不断进行，由最大ωmax线性减小到最小ωmin，即:

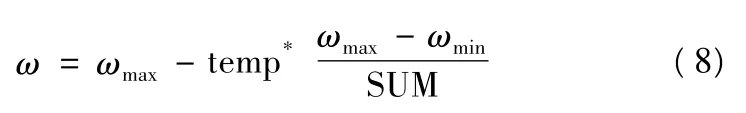
其中，temp*是当前迭代次数，SUM 是总的迭代次数。

2.2 基于PSO 优化的一体化保障设备使用工作量灰色预测模型

本文将最小误差平方和作为目标函数，采用粒子群算法直接求解a、b 和c，并代入式(5)，便可求出预测值^y(0)(k)，具体流程如图1 所示。

图1 PSO 算法流程

下面具体说明每一步流程:

1)初始化粒子群中粒子的状态(位置、速度):搜索空间维数设为三维，分别代表参数a、b 和c，粒子的初始位置即对应a、b 和c 的某一可能解;

2)计算粒子的适应度值: 将粒子的个体当前位置定义为最优位置pBest，初始粒子群中最优粒子所处的位置定义为全局最优位置gBest，以最小误差平方和为目标，把适应度值最小作为筛选最优粒子的条件，计算粒子(a、b、c)当前的适应度值:

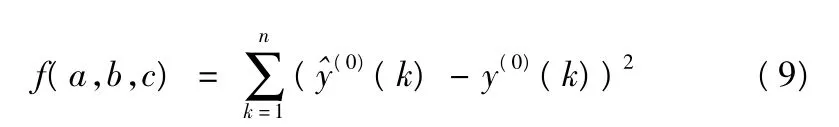
3)判断适应值是否满足收敛准则，若满足，直接进行步骤6);否则，继续进行步骤4);

4)更新迭代粒子群中所有粒子的速度与位置，若迭代过后的粒子适应度优于gBest 当前的适应度，则gBest 设为当前位置;

5)判断适应值是否满足收敛准则，若满足，直接进行步骤6);否则，继续进行步骤4);

6)输出全局最优位置gBest，即参数a、b 和c 的最优值，算法结束。

算法收敛准则设置为最大迭代次数或优化所得gBest 的适应度值达到预定的适应度阈值要求。

2.3 检验预测精度

构造初始数据序列:

由1.2 知预测模型模拟序列:

残差序列为

相对误差序列为

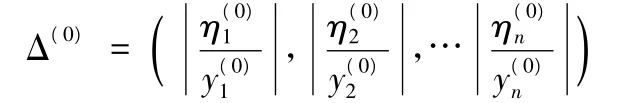
则Y(0)的均值、方差分别为

残差的均值、方差分别为

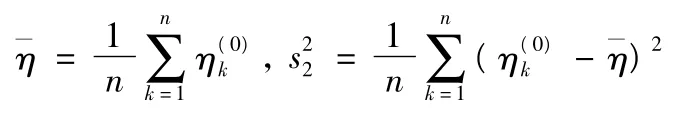
通过ρ、p 来检验也测精度，检验等级如表1 所示。

表1 精度检验等级参照表

3 实例计算

一体化装备保障要求部队进行多兵种的合成编制，目前，已经在全军范围内开展试点，某新型陆军数字化师合成装甲、军械、工程、防化等兵种，针对该师装备的所有通用装备，我们对这些装备使用维修过程中吊装设备的年度使用工作量进行预测，作为一个实例检验上述模型。

表2 为2010—2014年某数字化师吊装设备使用工作量(单位:10 d)。

那么，GM (1，1)的时间序列为

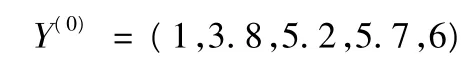
采用粒子群算法计算得:

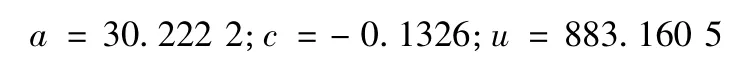
将上述3 个参数值代入式(1)～式(5)，对该师所有通用装备在2010—2014年的吊装设备使用工作量进行了重新“预测”，并预测出了2015年吊装设备的使用工作量，具体预测值见表3。

表2 吊装设备使用工作量

表3 预测结果

对预测结果作预测精度检验，得:

从结果可以看出，虽然两种预测的结果都是一级精度，但采用PSO 算法对灰微分方程的参数进行直接求解，不需构造背景值，ρ 值提高了25.6%，预测精度明显提高。因此，采用基于粒子群优化的灰色系统方法对一体化保障设备工作量的预测有利于提高一体化保障设备使用工作量确定的精确性，有助于提高一体化保障设备规划的科学性。

4 结论

一体化保障设备的使用工作量预测是确定一体化保障设备数量的基础，直接决定最终规划的保障设备数量是否满足部队的需求。实例验证表明，基于粒子群优化的灰色系统预测法具有贴合一体化保障系统实际，客观性强等特点，能够明显提高预测精度，不失为一种解决一体化保障设备使用工作量预测问题的方法。但是，一体化保障过程不可避免的存在着各种不确定因素，这些因素都将影响保障设备的使用工作量，要想确实做到精确预测保障设备的使用工作量仍然需要进一步的研究。

［1］梁婧，刘旭阳.一体化联合作战装备保障体系建设初探［J］.高电压技术，2007，18(6):10-13.

［2］梁海滨. 一体化装备保障［M］. 北京: 解放军出版社，2009.

［3］张侦英，康锐，王乃超，等.典型情况下保障设备满足率计算模型［J］.计算机集成制造系统，2010，16(10):2206-2210.

［4］郭红芬，刘福胜.利用排队模型优化保障设备数量［J］.装甲兵工程学院院报，2005，19(1):29-31.

［5］宋海涛，赵战彪，梅国建.基于灰色关联分析模型的战教比例优化研究［C］//装备保障过程建模理论方法与应用学术研讨会论文集.北京:兵器工业出版社，2009:406.

［6］岳洪江，刘思峰.灰色系统理论的发展、应用与扩散特征研究［J］.系统科学学报，2008，16(4):14-21.

［7］戴华娟.组合预测模型及其应用研究［D］.长沙:中南大学，2007.

［8］周达生，崔岩.铁路系统卫生人力资源预测研究——灰色系统模型的应用［J］.南京铁道医学院学报，1995，14(4):209-212.

［9］赵晓芬.灰色系统理论概述［J］.吉林省教育学院学报，2011，27(3):152-154.

［10］沈艳，郭兵，古天祥.粒子群优化算法及其与遗传算法的比较［J］.电子科技大学学报，2005，34(5):696-699.