温压弹爆炸冲击波作用下防护门的动力响应
苗朝阳,李秀地,孙 伟,杨 森,王起帆
(1.岩土力学与地质环境保护重庆市重点实验室(后勤工程学院),重庆 401311;2.后勤工程学院土木工程系,重庆 401311; 3.沈阳军区房地产管理局,沈阳 110000)
为有效打击坑道工事、掩体等防护工程,美国近年来开发了包括BLU-118B 温压炸弹、AGM -114M 温压导弹等多种温压弹。与传统高爆弹药相比,温压弹独特的爆炸毁伤效应主要体现在长持续时间高压冲击波和热杀伤,以及因爆炸耗氧造成的人员窒息等伤害。由于其独特的爆炸毁伤效应,温压弹特别适于打击坑道等封闭空间内的人员和设备。研究温压弹爆炸效应及其防护技术对提高坑道工程的战时生存能力具有重要意义[1]。由于防护门设置位置一般距坑道口部有一定的距离,温压弹爆炸产生的高温火球对近爆处影响较大,对远爆处影响较小。沿坑道传播的冲击波对防护门的破坏将是决定性因素,因此本文研究防护门在温压弹爆炸冲击波作用下的动力响应。
在温压弹坑道内爆炸冲击波效应研究方面,苟兵旺等[2]进行了温压炸药与TNT 坑道内爆炸实验,实测结果表明温压炸药坑道内爆炸冲击波超压、冲量普遍大于TNT。孔霖[3]通过等质量的温压炸药与TNT 坑道内爆炸试验研究,得出温压炸药在不同距离上冲击波正压持续时间均高于TNT。李世民等[4]利用AUTODYNA 软件模拟了温压炸药坑道内爆炸冲击波的传播规律,结果表明: 爆炸近区温压炸药冲击波超压低于TNT,远区高于TNT;而温压炸药爆炸冲击波冲量始终高于TNT,约为TNT 的1.4 倍。因此,从研究的角度出发,在坑道内相同位置爆炸产生的冲击波,相同质量的温压弹与TNT 常规弹相比可分为两类: 一是温压弹冲击波冲量大于TNT,但超压高于TNT,本文记为I 型温压弹; 二是温压弹冲击波冲量大于TNT,但超压低于TNT,本文记为II 型温压弹。
目前,传统高爆炸药爆炸冲击波作用下防护门的动力响应研究已取得一些成果,而温压弹爆炸冲击波作用下防护门的动力响应研究几乎处于空白。为此,本文利用大型有限元软件ANSYS/LS-DYNA[5]建立了分离式钢筋混凝土防护门动力响应的数值计算模型,在试验实测数据验证的基础上,针对温压弹冲击波的特点,分析了防护门的动力响应特点,并与TNT 冲击波的作用结果进行了对比。
1 数值分析模型及模型验证
1.1 数值计算模型
防护门取钢筋混凝土单扇门,长(Y 方向)2 040 mm、宽(X 方向)1 500 mm、厚(Z 方向)270 mm,门框厚度60 mm,门框与门体接触宽度为50 mm。采用单轴抗压强度为40 MPa的混凝土,双层双向配置φ18HRB335 受拉钢筋(X 方向)及φ10HRB335 分布钢筋(Y 方向),配置φ8HRB335 单肢箍筋(Z 方向),受拉及分布钢筋间距90 mm,箍筋间距180 mm。钢筋混凝土采用分离式共节点建模方式,由于对称性,建立四分之一模型。网格尺寸取15 mm,门体混凝土共划分为61 200 个单元,钢筋划分为3 180 个单元,门框划分为1 856 个单元。统一使用单位为g-mm-ms。防护门的有限元模型,见图1。

图1 防护门有限元模型
1.2 材料模型及参数
LS-DYNA 中适合模拟爆炸冲击作用下的混凝土材料模型有MAT072R3,MAT084,MAT159 等,本文选用MAT_CONCRETE_DAMAGE_REL3 (MAT072R3)。该模型考虑了混凝土材料的应变率效应,参数输入简便而且能够较好的模拟爆炸冲击作用下混凝土的动态响应问题[6]。选择SOLID164 3D 单元模拟混凝土,采用单点积分算法。钢筋使用塑性随动模型MAT_ PLASTIC_KINEMATIC(MAT3),选择BEAM161梁单元进行模拟,采用2 ×2 Gauss 积分算法。选择刚体MAT_RIGID 模型模拟门框。混凝土的抗拉及抗压强度动载增大系数DIF 均采用欧洲混凝土规范CEB[7]推荐的公式计算,钢筋的动载增大系数DIF 采用Malvar[8]提出的公式计算。混凝土及钢筋材料参数,分别见表1、表2。

表1 混凝土材料参数

表2 钢筋材料参数
1.3 边界条件
防护门边界条件通常考虑简支或设置接触,杨心宇等[9]通过对防护门在不同约束条件下的动力响应进行分析,表明防护门配筋按四边简支计算偏于保守; 陆新征等[10]通过设置门扇与门框,门轴与轴瓦两种接触研究了抗爆门的动力响应,并得到了抗爆门的反弹力。本文在考虑防护门的实际支承情况下设置了简化接触,即门扇四边与门框间设置Automatic Contact,Surface to Surface 接触类型。
1.4 荷载的确定
结合文献[2 -4]温压炸药爆炸冲击波研究结果,本文计算中考虑以下3 种荷载工况,分别模拟上述等质量的I 型、II型温压弹及TNT 的爆炸荷载。其中I 型与II 型温压弹冲量相同,其冲量为TNT 冲量的1.45 倍;冲击波衰减速度II 型温压弹最慢,TNT 最快,I 型温压弹介于前两者之间。简化后的3 种突加三角形衰减荷载,见图2。

图2 荷载时程曲线
1.5 模型验证
文献[11]对钢筋混凝土板在冲击波作用下的动力响应进行了研究,为验证本文上述数值模型的可靠性,对文献[11]中实验NSC-NR 进行模拟。模拟中按照实验加载冲击波及其边界条件控制,跨中位移时程曲线实验及数值模拟计算结果,见图3。

图3 计算模型的验证
可见数值计算获得曲线与实验实测曲线取得了较好的一致性;数值计算跨中挠度最大值为212.7 mm,与实验中实测值221 mm 误差仅为3.76%,表明本文提出的数值模型可以较好的模拟钢筋混凝土构件在爆炸冲击波作用下的动力响应。
2 数值模拟结果分析
2.1 有效塑性应变
防护门迎爆面的有效塑性应变见图4。数值计算表明,TNT、I 型、II 型温压弹爆炸冲击波作用下,防护门有效塑性应变首先从防护门与门框接触内边缘支座位置开始发展。随着爆炸作用时间增加,防护门塑性变形由两侧长边方向不断向内扩展,混凝土塑性变形严重的部位产生受压和受拉裂缝,最后塑性变形区稳定,显示出在爆炸荷载作用后防护门的残余变形情况。研究表明,TNT 作用下,防护门塑性区尚未贯通,在长边支座、门扇中间钢筋的位置有裂缝,此区域钢筋与混凝土变形不一致,导致钢筋位置处的混凝土塑性变形过大而破坏;II 型温压弹作用下,防护门门扇两侧中间位置出现较大塑性区,门扇中及门的四角产生大量受压裂缝;I 型温压弹作用下,塑性区扩展至防护门整体,防护门破坏严重。

图4 不同爆炸荷载下防护门有效塑性应变对比
2.2 挠度及转角
防护门背爆面跨中位移时程曲线,见图5。由图可见,防护门跨中挠度先增大后减小,最后残余变形保持稳定。I 型、II 型温压弹及TNT 作用下防护门跨中最大挠度分别为93.6 mm、58.6 mm、43.5 mm;相应的达到最大挠度的时间分别为12 ms、13 ms、10 ms。I 型温压弹作用下防护门的挠度始终最大;II 型温压弹作用下,防护门初期(8 ms 前)响应与TNT 相差不大,但后期(8 ms 后)高于TNT 作用的情况。美军规范TM5-1300[12]指出当构件响应时间小于荷载作用时间的3倍时,构件的响应不仅与冲量有关还与压力脉冲有关。计算中3 种工况构件达到最大响应的时间均小于荷载作用时间的3 倍,因此,温压弹的高毁伤效能不仅与其高冲量相关,也与其冲击波衰减速率相关。

图5 防护门背爆面跨中位移时程曲线
防护门支座处转角θ 可由下式计算

式(1)中:X 为防护门跨中挠度;B 为防护门宽度。
由此可得I 型温压弹、II 型温压弹、TNT 作用下防护门转角分别为7°26'、4°40'、3°28'。根据文献[12],当支座转角达到2°时,钢筋混凝土受弯构件受压混凝土压碎;当支座转角为4°时,构件丧失完整性并破坏。因此,TNT 作用下防护门受压区混凝土虽已压碎,但防护门尚未丧失整体稳定性,使用中能够抗得住一次打击作用;而I 型、II 型温压弹作用下防护门已丧失整体完整性,破坏严重。特别是I 型温压弹作用下防护门最大挠度及转角达TNT 作用下的2 倍以上。因此温压弹高冲量长持时冲击波作用下,防护门的动力响应要大得多。
2.3 破坏模式
对于弯曲破坏,根据上述转角计算结果,3 种荷载工况下防护门受压区均有混凝土压碎;I、II 型温压弹作用下防护门受压区混凝土大部分失效,大量钢筋被拉断,挠度及转角大,破坏严重。但TNT 作用下防护门挠度及转角均较小,钢筋尚未拉断,弯曲破坏并不严重。
很多学者对钢筋混凝土板的破坏模式进行了研究,但破坏标准不统一[13]。对于剪切破坏,本文按照美军规范TM5 -1300中如下公式计算钢筋混凝土的抗剪强度
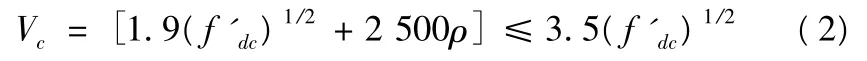
式(2)中: f'dc为混凝土的动力极限抗压强度(psi);ρ 为支座处受拉钢筋的配筋率。
C40 混凝土动力极限抗压强度取47.6 MPa,支座处配筋率
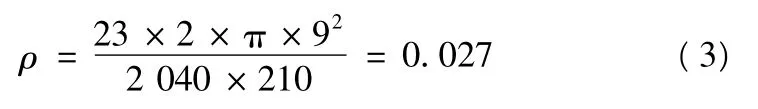
式(3)代入式(2)可得: Vc=1.56 MPa。
本文取动力荷载作用下钢筋混凝土的抗剪强度动载提高系数为2.0[14]。因此,当防护门单元剪应力超过1.56 ×2 =3.12 MPa 时认为该处发生剪切破坏。3 种工况下防护门达到最大挠度时剪应力图,见图6。

图6 防护门剪应力图
由图6 可见,在3 种工况下,图中蓝色区域的剪应力均未达到极限抗剪强度值,不会发生破坏; 而红色单元剪应力均超过了防护门的抗剪强度,在图中所示位置产生斜剪裂缝,发生剪切破坏。I、II 型温压弹作用初期防护门支座处剪切破坏特征明显,随着防护门挠度的增大,剪切裂缝向跨中发展,表现出明显的弯剪破坏特征;TNT 作用初期防护门支座附近产生剪切裂缝,但随着防护门挠度的增大,这些剪切裂缝并没有进一步发展。
3 结论
本文在实验验证的基础上建立了温压弹爆炸冲击波作用下防护门动力响应的数值计算模型,通过对3 种荷载工况下防护门的动力响应进行数值模拟,得出以下结论:
1)温压弹高冲量冲击波作用下防护门的挠度、转角及变形等大于TNT 作用下的情况,为有效抗温压弹打击,对防护门进行改进很有必要。
2)由于超压及冲击波衰减速度不同,等冲量温压弹对防护门的破坏效果亦不相同,防护门的响应不仅与温压弹爆炸冲击波的高冲量有关,还与其冲击波衰减速率有关。
3)本文3 种荷载工况下,防护门均有相当程度的剪切与弯曲破坏。温压弹作用下防护门的主要破坏模式为弯剪耦合破坏,整体性已丧失,破坏严重;TNT 作用下防护门主要破坏模式为剪切破坏,但其整体性未丧失,可抗一次打击。设计及加固防护门时应提高其抗弯能力,同时为减少剪切裂缝,应加密支座附近处箍筋。
[1]周丰峻.信息化战争条件下作战工程保障和工程兵多样化军事行动任务探索[C]//中国土木工程学会防护工程分会第十二次学术年会论文集,张家界,2010(8):1-6.
[2]苟兵旺,李芝荣,闫潇敏.复杂坑道内温压炸药冲击波实验研究[J].火工品,2014(2):41-45.
[3]孔霖,苏健军,李芝荣.不同装药坑道内爆炸冲击波传播规律的试验研究[J].火工品,2012(3):21-24.
[4]李世民,李晓军,李洪鑫.温压炸药坑道内爆炸冲击波的数值模拟研究[J]. 应用力学学报,2012,29(5): 595-601.
[5]LS-DYNA keyword uer’s manual[M]. Livemore,California:livemore software technology corporation,2007,5,Version 971.
[6]Tu Z G,Lu Y.Evaluation of typical concrete material models used in hydrocod es for high dynamic resp onse simulations[J].International Journal of Impact Engineering,2009,(36)8:132-146.
[7]Du B C E I. CEB-FIP Model Code 1990[S]. Redwood Books,Trowbridge,Wiltshire,UK,1990.
[8]Malvar L J.Review of static and dynamic properties of steel reinforcing bars[J]. ACI Materials Journal,1998,95(5):609-614.
[9]杨心宇,赵跃堂,周泽鑫.平板防护门不同约束形式下的动力响应[J].爆破,2014,312(2):47-56.
[10]陆新征,江见鲸.抗爆门结构考虑接触影响的动力有限元分析[J].力学与实践,2003,25 (5):24-26.
[11]TM5-1300,The design of structures to resist the effects of accidental explosions,Technical manual [M]. Washington DC: US Department of the Army,Navy,and Air Force,1990.
[12]阎石,张亮,王丹.钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J].沈阳建筑大学学报:自然科学版,2005,21(3):177-180.
[13]Chung H W.Shear strength of concrete joints under dynamic loads[J].Concrete,1978,12(3):27-29.

