温压弹爆炸冲击波作用下防护门破坏模式研究
李秀地, 耿振刚, 苗朝阳, 杨 森
(1.后勤工程学院 土木工程系 岩土力学与地质环境保护重庆市重点实验室,重庆 401311;2. 92303部队,山东 青岛 266404)
温压弹爆炸冲击波作用下防护门破坏模式研究
李秀地1, 耿振刚1, 苗朝阳1, 杨森2
(1.后勤工程学院 土木工程系 岩土力学与地质环境保护重庆市重点实验室,重庆401311;2. 92303部队,山东青岛266404)
为研究温压弹爆炸冲击波作用下防护门的破坏模式,利用ANSYS/LS-DYNA软件建立了考虑材料应变率效应的分离式钢筋混凝土防护门数值计算模型。对防护门加载温压弹爆炸冲击波波形,分析了防护门的挠度、转角和剪应力,并与TNT的作用结果进行了对比。结果表明:温压弹爆炸冲击波作用下,随着距爆炸源距离的增加,防护门的破坏模式由直剪破坏、弯剪耦合破坏逐渐变为弯曲破坏;防护门的响应与温压弹爆炸冲击波的高冲量有关,温压弹爆炸冲击波作用下防护门的破坏程度大于TNT的作用结果;防护门跨中速度值可以用来快速评估防护门的破坏模式。
爆炸力学;温压弹;钢筋混凝土;防护门;破坏模式
近年来以美国为首的西方国家对发展温压武器的兴趣越来越浓厚,开发了包括BLU-118B温压炸弹、AGM-114M温压导弹等多种温压弹。与传统高爆弹药相比,温压弹独特的爆炸毁伤效应主要体现在长持续时间高压冲击波和热杀伤,以及因爆炸耗氧造成的人员窒息等伤害,特别适于打击坑道等封闭空间内的人员和设备。研究温压弹爆炸效应及其防护技术对提高坑道工程的战时生存能力具有重要意义[1]。坑道内的防护门距离口部一般较远,热杀伤不是主要威胁,而爆炸冲击波将是防护门破坏的决定性因素。因此,本文对温压弹爆炸冲击波作用下防护门的破坏模式进行研究。
温压弹爆炸冲击波研究方面,苟兵旺等[2-3]进行了温压炸药与TNT坑道内爆炸试验,实测了坑道内爆炸冲击波波形,并进行了对比。防护门破坏模式研究方面,阎石等[4]研究了等冲量的TNT爆炸冲击波不同加载速率下钢筋混凝土板的破坏模式,结果表明随着冲击波超压峰值的增大,钢筋混凝土板破坏模式由弯曲破坏逐渐变为剪切破坏;汪维等[5]研究了不同装药量TNT近爆作用下钢筋混凝土板的破坏,结果表明随着装药量的增大,钢筋混凝土板的破坏模式由整体弯曲破坏逐渐变为局部冲切破坏。温压弹爆炸冲击波作用下防护门的破坏模式研究几乎处于空白,本文采用ANSYS/LS-DYNA[6]有限元软件建立钢筋混凝土防护门的分离式共节点计算模型,在试验实测数据验证的基础上,分析温压弹爆炸冲击波作用下防护门的破坏模式,并与TNT的作用结果进行对比。
1 温压弹坑道内爆炸冲击波
基于坑道堵口爆炸试验实测数据[7]验证,利用ANSYS/LS-DYNA软件建立了坑道内爆炸冲击波三维数值计算模型。分别计算了一种RDX基含铝温压炸药(RDX/AL/黏结剂=68/28/4,文中记为TBE)和TNT各75 kg堵口爆炸时,坑道内爆炸冲击波的传播规律,得到不同距离处爆炸冲击波波形,如图1所示。
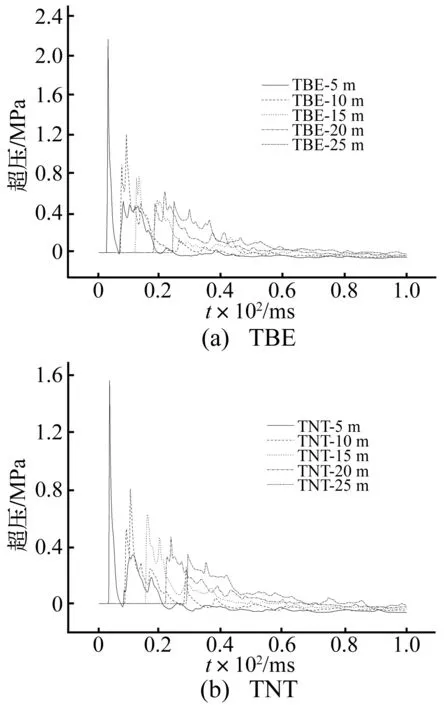
图1 冲击波波形Fig.1 Blast wave in tunnel
由图1可知,坑道内温压炸药爆炸冲击波与TNT爆炸冲击波波形均为锯齿状,且随着传播距离的增大,超压逐渐衰减,正相作用时间逐渐增加。但温压炸药爆炸冲击波的传播速度更快、超压更高、正相作用时间更长。这是由于温压炸药中添加的铝粉等产生后燃反应,增大了温压炸药的爆炸冲量,提高了温压炸药的爆炸威力。本文计算条件下的温压炸药冲击波入射超压峰值约为TNT的1.23倍~1.50倍,冲量约为TNT的1.42倍~1.62倍,这与文献[2-3]坑道内实测比值基本相同。
2 防护门数值分析模型的建立与验证
2.1防护门计算模型
防护门选取钢筋混凝土单扇门,长2 m、宽1.5 m、厚0.27 m,门框厚0.06 m,门框与门体接触宽度为0.05 m。双层双向布置φ18HRB335横向受拉钢筋和φ10HRB335纵向分布钢筋,布置φ8HRB335单肢箍筋,受拉及分布钢筋间距0.09 m,箍筋间距0.18 m。采用分离式共节点方式建模,由于对称性,建立四分之一模型。网格尺寸取0.015 m,防护门的有限元模型如图2所示。

图2 防护门有限元模型Fig.2 Finite model of blast door
2.2材料模型
混凝土选用MAT_CONCRETE_DAMAGE_ REL3材料。该模型考虑了混凝土材料的应变率效应,仅需要输入密度、泊松比和单轴抗压强度三个参数,便能较好的模拟爆炸冲击作用下混凝土的动态响应问题[8]。选用LS-DYNA中单轴抗压强度为40 MPa的混凝土,混凝土密度取2.4×103kg/m3,泊松比取0.2。钢筋使用塑性随动模型MAT_PLASTIC_KINEMATIC,门框选择刚体模型MAT_RIGID。混凝土的抗拉及抗压强度动载增大系数DIF均采用欧洲混凝土规范CEB[9]推荐的公式计算,钢筋的动载增大系数DIF采用Malvar[10]提出的公式计算。钢筋材料参数如表1所示。

表1 钢筋材料参数
2.3边界条件
防护门边界条件通常考虑简支或设置接触。杨心宇等[11]通过对防护门在不同约束条件下的动力响应进行分析,表明防护门配筋按四边简支计算偏于保守;陆新征等[12]通过设置门扇与门框、门轴与轴瓦两种接触研究了抗爆门的动力响应,并得到了抗爆门的反弹力。本文在考虑防护门的实际支承情况下设置了简化接触,即门扇与门框间设置Automatic Contact、Surface to Surface 接触类型。
2.4爆炸荷载的施加
LS-DYNA可以通过流固耦合算法、CONWEP算法和直接加载法3种方法对防护门施加爆炸冲击波荷载。CONWEP算法可以方便地计算自由场TNT爆炸冲击波荷载,但无法计算坑道内温压炸药的爆炸冲击波。流固耦合算法通常用于计算近爆作用下结构动力响应[5,13],防护门距坑道口部通常达到10 m以上,运用流固耦合算法模型单元数量十分惊人,计算甚至难以进行。直接加载法将冲击波曲线作为面荷载直接施加于防护门上,模型简单、概念清晰、计算效率高,已被广泛应用于研究钢筋混凝土构件在爆炸冲击波作用下的动力响应问题[12],本文运用直接加载法研究温压弹冲击波作用下防护门的破坏模式。将图1所示温压弹和TNT坑道内入射冲击波通过下式转换为反射冲击波[14]:
(1)
式中:ΔPm、ΔPrm分别为入射冲击波和正反射冲击波超压峰值,MPa;n为正反射系数,按表2取值;当ΔPm为表中范围内其它值时,用内插法确定n值。

表2 空气冲击波正反射系数[14]
计算中将通过式(1)计算所得冲击波正反射波形直接加载于防护门上,设置工况如表3所示。
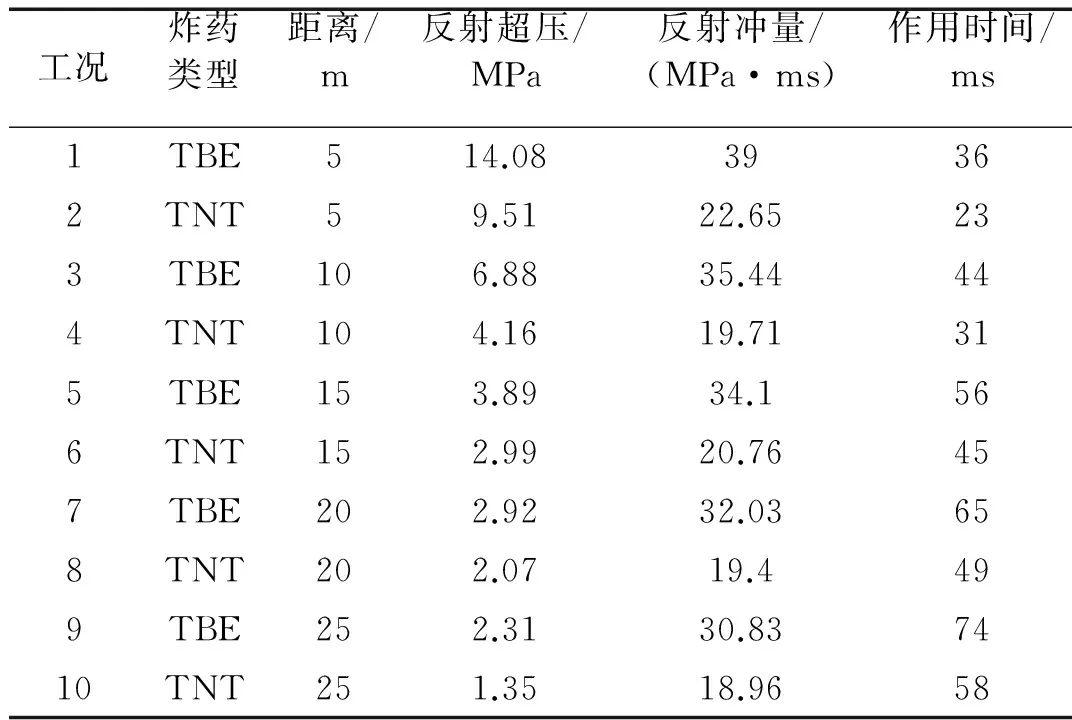
表3 计算工况
2.5计算模型的验证
文献[15]对钢筋混凝土板在冲击波作用下的动力响应进行了研究,为验证本文上述数值模型的可靠性,对文献[15]中实验NSC-NR进行模拟。采用直接加载法,按照实验实际边界条件,跨中位移时程曲线实验及数值模拟计算结果,如图3所示。
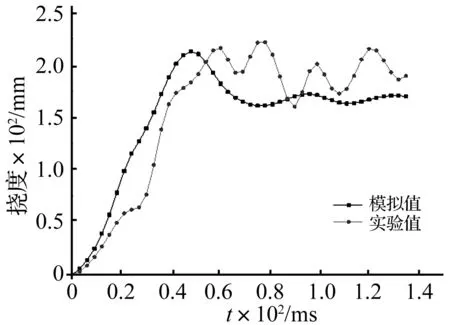
图3 计算模型的验证Fig.3 Model validation
由图3可知,数值计算所得曲线与试验实测曲线取得了较好的一致性;数值计算跨中挠度最大值为212.7 mm,与试验实测值221 mm误差为3.76%,表明本文提出的数值计算模型可以较好地模拟钢筋混凝土构件在爆炸冲击波作用下的动力响应。
3 防护门破坏模式分析
钢筋混凝土防护门在爆炸荷载作用下的破坏模式通常有直剪破坏、弯曲破坏、弯剪耦合破坏等整体破坏和混凝土压碎、开裂、破片等局部破坏[15],本文主要从整体破坏的角度分析防护门的破坏模式。以工况1、5和9作为典型荷载,研究温压弹堵口爆炸作用下,防护门在近、中和远3个位置的破坏模式。
3.1弯曲破坏分析
以防护门支座处转角作为其弯曲破坏特征进行研究,根据文献[17],配单肢箍筋时,当支座转角达到4°,钢筋混凝土受弯构件丧失抗弯承载能力;当支座转角到达12°,构件将因丧失整体性而完全破坏。本文计算以支座处转角4°和12°为界,当支座处转角小于4°时,防护门发生轻度弯曲变形,视为未破坏;当支座处转角大于4°时,防护门发生严重弯曲破坏;当支座处转角小于12°时,防护门虽遭受破坏,但抗住了一次打击作用。3种工况下防护门背爆面跨中位移时程曲线如图4所示。
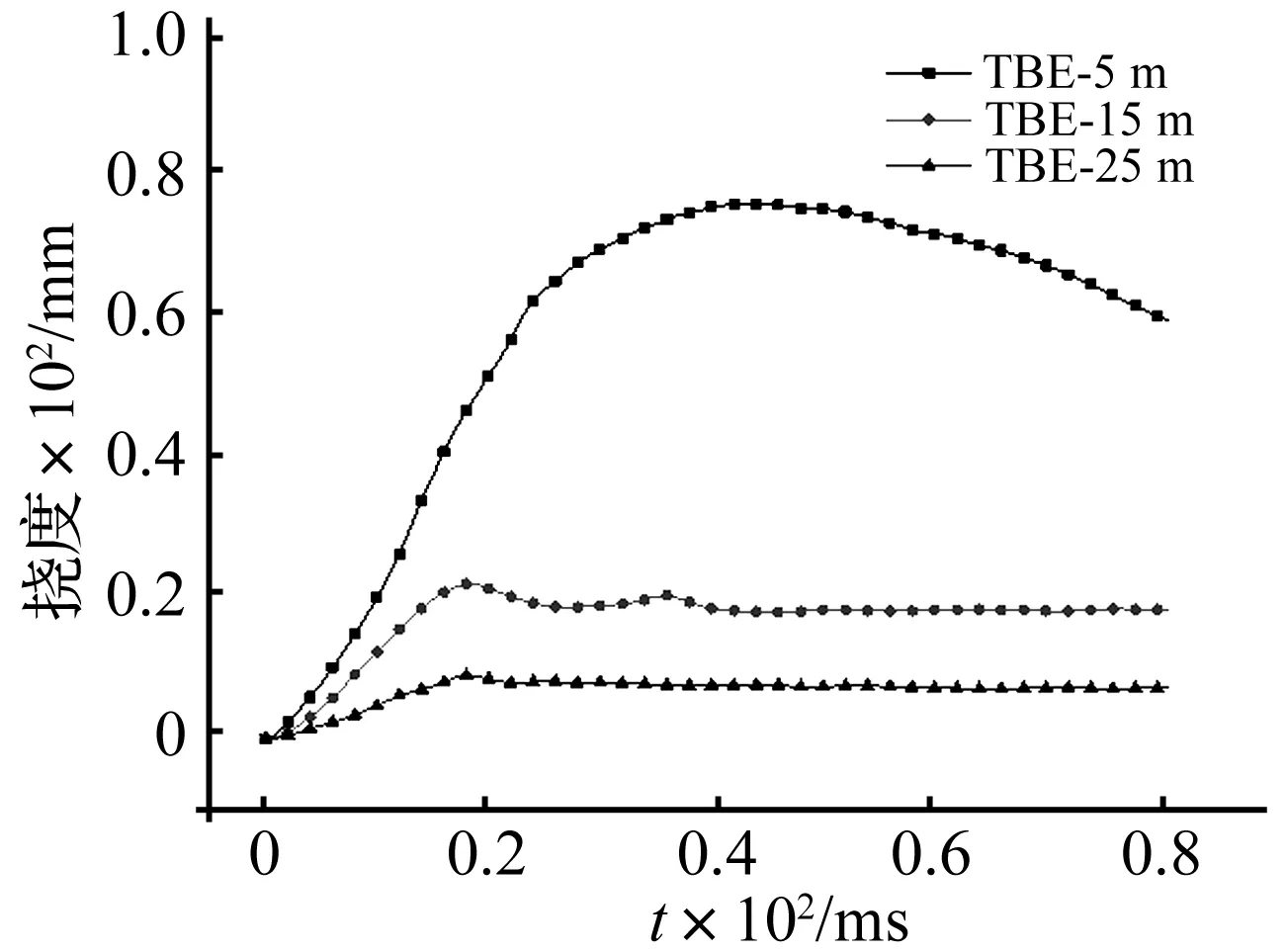
图4 跨中位移时程曲线Fig.4 History curve of mid span displacement
由图4可知,防护门跨中挠度先增大后减小,最后残余变形保持稳定。温压弹堵口爆炸时防护门距口部5 m、15 m和25 m情况下,跨中最大挠度分别为72.3 cm、18.8 cm、8.7 cm。防护门支座处转角θ可由下式计算:
(2)
式中:X为防护门跨中挠度;B为防护门宽度。
将工况1、5和9计算得到的防护门跨中最大挠度分别代入式(2),可得防护门转角分别为43.9°、14.8°和6.6°。因此,工况1和5条件下,防护门均因丧失整体性而完全破坏;工况9条件下,防护门虽未丧失整体性,但已发生严重弯曲破坏。
3.2剪切破坏分析
抗压强度为40 MPa的混凝土,其抗剪强度为[16]:
利用LS-PREPOST后处理软件,以此抗剪强度为标准,可以清晰地观察防护门受剪失效单元的位置。选取爆炸冲击波作用初期(t=1 ms)和防护门达到最大挠度前典型剪切破坏的时刻,不同工况下防护门的剪切破坏形态如图5所示。图中浅色区域为受剪失效单元。
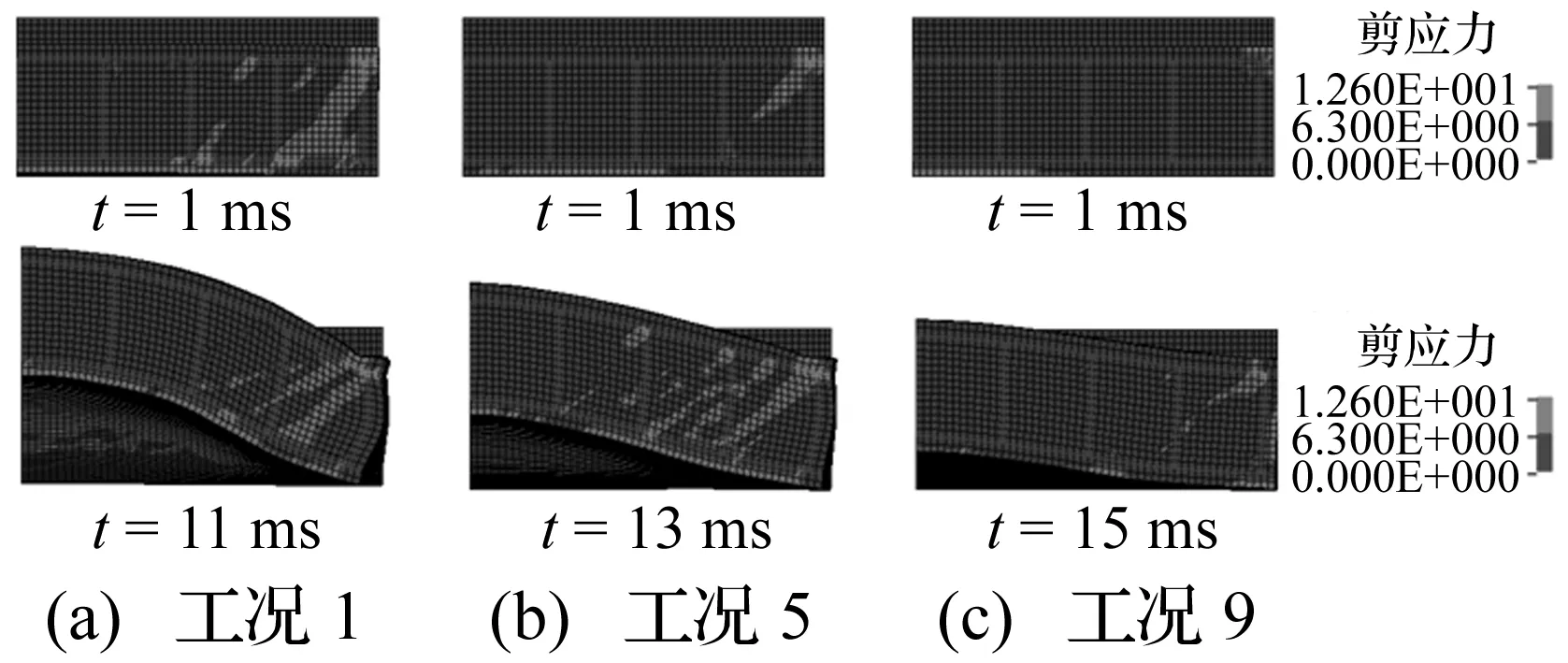
图5 防护门剪切破坏形态Fig.5 Shear failure mode of blast door
由图5(a)可知,对于工况1,在冲击波作用初期(t=1 ms),防护门尚未达到最大挠度,支座处已产生较宽的贯通剪切裂缝,表明防护门发生了直接剪切破坏。达到最大挠度前,防护门支座处剪切裂缝进一步发展(t=11 ms),防护门门体沿支座处剪切裂缝发展方向,被冲击波“推出”门框外。
由图5(b)可知,对于工况5,在冲击波作用初期(t=1 ms),防护门支座处有较宽的剪切裂缝,但没有贯通。随着冲击波作用时间的增加,防护门跨中剪跨区出现多条斜剪裂缝(t=13 ms),部分已经贯通,有明显的弯剪耦合破坏特征。
由图5(c)可知,对于工况9,在冲击波作用初期(t=1 ms),防护门仅有少量支座附近单元发生剪切失效。随着冲击波作用时间的增加,防护门多个位置有剪切裂缝(t=15 ms),但裂缝宽度较窄,尚未完全贯通。
由以上分析可知,工况1防护门主要破坏模式为直剪破坏,防护门被完全摧毁。工况5防护门主要破坏模式为弯剪耦合破坏,防护门破坏严重,工况9防护门主要破坏模式为弯曲破坏。
4 温压弹与TNT作用下防护门破坏模式对比
按照上述破坏模式分析方法,计算表3所示各工况下,防护门跨中挠度、转角、达到最大位移时间Tmax、跨中最大速度Vmax和主要破坏模式分别如表4所示。
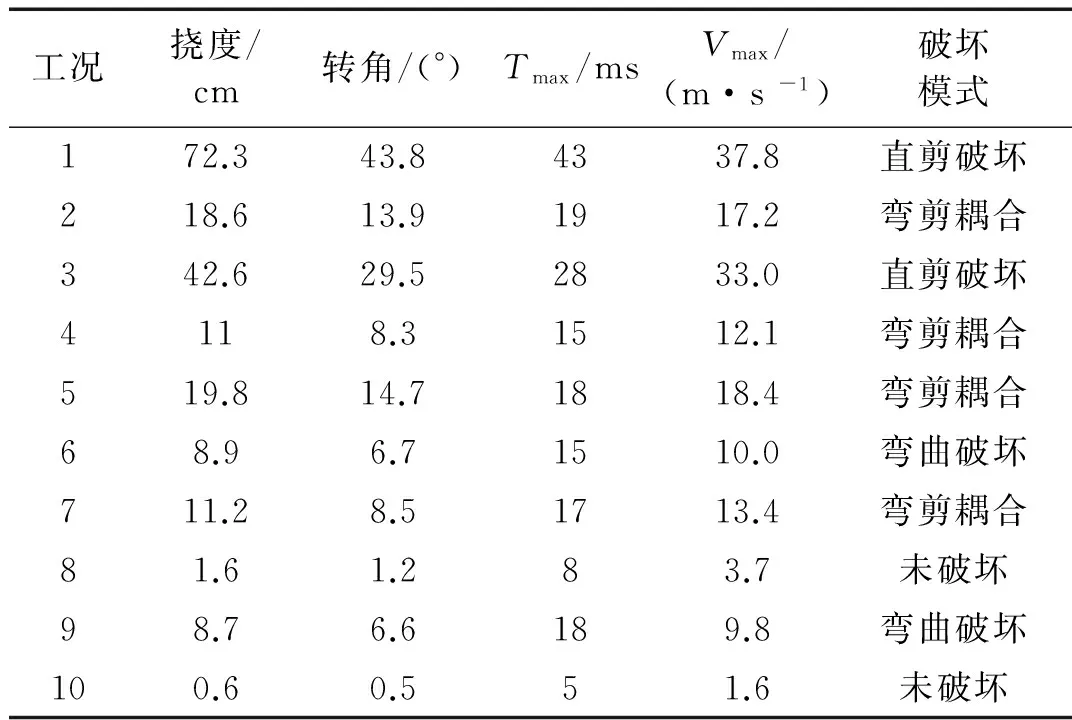
表4 防护门计算结果
由表4可知,随着距爆炸源距离的增加,本文计算温压弹和TNT爆炸冲击波作用下防护门的挠度、转角和跨中最大速度均不断地减小。相同位置处,温压弹爆炸冲击波作用下防护门的挠度、转角和跨中最大速度大于TNT作用的情况,防护门的破坏模式不同于TNT作用的情况。距坑道口部大于15 m时,防护门可以有效防护TNT爆炸冲击波作用;但在温压弹爆炸冲击波作用下,防护门仍然严重破坏。表明温压弹具有更高的爆炸威力。
以工况4与工况7为例,分析温压弹爆炸冲击波超压峰值低于TNT情况下防护门的毁伤。工况4 TNT爆炸冲击波超压为工况7温压弹爆炸冲击波超压的1.43倍,但温压弹爆炸冲击波作用下防护门最大位移却大于TNT的作用。这是由于温压弹冲击波冲量达TNT冲击波冲量的1.62倍的结果,表明温压弹的高毁伤效能与其高冲量有关。
由表4并结合图4可知,不同破坏模式时,防护门跨中位移时程曲线初始段斜率(即跨中速度值)不同。大量计算表明,跨中速度值可以用来快速判断防护门的破坏模式。本文计算条件下,跨中速度值大于18.4 m/s时,防护门发生直剪破坏;跨中速度值为10.0~18.4 m/s时,防护门发生弯剪耦合破坏;跨中速度值为3.8~10.0 m/s时,防护门发生弯曲破坏;跨中速度值小于3.8 m/s时,防护门不发生破坏。
5 结 论
基于试验数据验证,建立了防护门的数值计算模型,研究了温压弹爆炸冲击波作用下防护门的破坏模式,并与TNT的作用结果进行了对比,得出以下结论:
(1) 温压弹爆炸冲击波作用下,随着防护门距爆炸源距离的增大,防护门的破坏模式由近爆处的直剪破坏变为中爆处的弯剪耦合破坏和远爆处的弯曲破坏。
(2) 防护门的响应与温压弹爆炸冲击波的高冲量有关,温压弹爆炸冲击波作用下坑道内相同位置处防护门的破坏程度大于TNT作用的情况,防护门的破坏模式与TNT作用时不尽相同。
(3) 防护门的破坏模式可以通过跨中速度值快速评估。本文计算条件下,跨中速度值大于18.4 m/s时,防护门发生直剪破坏;跨中速度值为10.0~18.4 m/s时,防护门发生弯剪耦合破坏;跨中速度值为3.8~10.0 m/s时,防护门发生弯曲破坏;跨中速度小于3.8 m/s时,防护门不发生破坏。
[1] 周丰峻. 信息化战争条件下作战工程保障和工程兵多样化军事行动任务探索[C]//中国土木工程学会防护工程分会第十二次学术年会论文集.张家界,2010:1-6.
[2] 苟兵旺,李芝荣,闫潇敏,等. 复杂坑道内温压炸药冲击波实验研究[J]. 火工品,2014(2):41-45.
GOU Bingwang, LI Zhirong, YAN Xiaomin, et al. Experimental study on shock wave effects of thermo-baric explosive in complex tunnel[J]. Initiators and Pyrotechnics, 2014(2):41-45.
[3] 孔霖,苏健军,李芝荣,等. 不同装药坑道内爆炸冲击波传播规律的试验研究[J]. 火工品,2012(3):21-24.
KONG Lin, SU Jianjun, LI Zhirong, et al. Test study on explosion shock wave propagation of different explosives inside tunnels[J]. Initiators and Pyrotechnics, 2012(3):21-24.
[4] 阎石,张亮,王丹. 钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J]. 沈阳建筑大学学报:自然科学版,2005, 21(3):177-180.
YAN Shi, ZHANG Liang, WANG Dan. Failure mode analysis for RC slab under explosive loads[J]. Journal of Shenyang Architecture and Civil Engineering University:Nature Science Edition, 2005, 21(3):177-180.
[5] 汪维,张舵,卢芳云,等. 方形钢筋混凝土板的近场抗爆性能[J]. 爆炸与冲击,2012,32(3): 251-258.
WANG Wei, ZHANG Duo, LU Fangyun, et al. Anti-explosion performances of square reinforced concrete slabs under close-in explosions[J]. Explosion and Shock Waves,2012,32(3):251-258.
[6] LS-DYNA keyword uer’s manual[M]. Livemore, California: Livemore Software Technology Corporation, 2007, 5, Version 971.
[7] 吴云泉, 许金余, 陈海天,等. 坑道口部爆炸冲击波压力传播规律[J]. 空军工程大学学报:自然科学版,2009,10(5):90-94.
WU Yunquan, XU Jinyu, CHEN Haitian, et al. Study of shock wave pressure propagation laws of the explosion at the tunnel entrance[J]. Journal of Air Force Engineering University:Natural Science Edition, 2009, 10(5):90-94.
[8] TU Z G, LU Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J]. International Journal of Impact Engineering, 2009,36:132-146.
[9] DU B C E. CEB-FIP model code 1990: Design code[M]. London: Thomas Telford Ltd., 1990.
[10] MALVAR L J.Review of static and dynamic properties of steel reinforcing bars[J].ACI Materials Journal, 1998, 95(5):609-614.
[11] 杨心宇,赵跃堂,周泽鑫. 平板防护门不同约束形式下的动力响应[J]. 爆破, 2014, 2(31):47-56.
YANG Xinyu, ZHAO Yuetang, ZHOU Zexin. Dynamic response of blast door under different forms of constrains[J]. Blasting, 2014, 2(31):47-56.
[12] 陆新征,江见鲸. 抗爆门结构考虑接触影响的动力有限元分析[J]. 力学与实践, 2003,25(2):24-26.
LU Xinzheng, JIANG Jianjing. Safety assessment of blast-resistant doors using dynamic finite element method and contact analysis[J]. Mechanics in Engineering, 2003,25(2):24-26.
[13] 龚顺风,邓欢,朱升波,等. 近爆作用下钢筋混凝土板动态破坏的数值模拟研究[J]. 振动与冲击,2012,31(2):20-24.
GONG Shunfeng, DENG Huan, ZHU Shengbo, et al. Numerical simulation for dynamic failure of a reinforced concrete slab under close-in explosion[J]. Journal of Vibration and Shock, 2012,31(2):20-24.
[14] 方秦,柳锦春. 地下防护结构[M]. 北京:中国水利水电出版社,2010.
[15] THIAGARAJAN G, KADAMBI A V, ROBERT S, et al. Experimental and finite element analysis of doubly reinforced concrete slabs subjected to blast loads[J]. International Journal of Impact Engineering, 2015,75:162-173.
[16] TRIVEDI N, SINGH R K. Prediction of impact induced failure modes in reinforced concrete slabs through nonlinear transient dynamic finite element simulation[J]. Annals of Nuclear Energy, 2013,56:109-121.
[17] TM5-1300. The design of structures to resist the effects of accidental explosions[M].Washington DC:US Department of the Army, Navy, and Air Force, 1990.
Failure mode of a blast door subjected to the explosion wave of a thermobaric bomb
LI Xiudi1, GENG Zhengang1, MIAO Chaoyang1, YANG Sen2
(1. Chongqing Key Laboratory of Geomechanics & Geoenvironment Protection in Department of Civil Engineering,Logistical Engineering University, Chongqing 401311, China;2. Unit 92303, Qingdao 266404, China)
To reveal the failure mode of a blast door subjected to the explosion wave of a thermobaric bomb, a separate reinforced concrete numerical model considering strain rate effects of a blast door was established with the dynamic finite element software ANSYS/LS-DYNA. The explosion wave of a thermobaric bomb was loaded on the blast door and the deflection and shear stress of the blast door were analyzed and compared with the shock wave of TNT. The results show that with the distance from explosion increasing, the failure mode of blast door under the thermobaric bomb gradually changes from punching shear failure and mixed flexural-shear failure to flexural failure. The dynamic response of the blast door is related to the high impulse of the thermobaric bomb, and the damage of the blast door under the thermobaric bomb is more serious than that under TNT. The velocity of the mid span can be used to estimate the failure mode of the blast door.
mechanics of explosion; thermobaric bomb; reinforced concrete; blast door; failure mode
国家部委基金(CY213J009)
2015-09-29修改稿收到日期:2015-12-31
李秀地 男,博士,教授,1970年生
O383
A
10.13465/j.cnki.jvs.2016.16.032

