基于区间数比较可能度的主要防御方向选择

宋占岭，王 锐

(总参炮兵训练基地，河北宣化 075100)

主要防御方向是防御者集中兵力兵器抗击敌人进攻的空间指向，是防御决心的重要内容［1］。文献［2］中将选择主要方向归结为有限方案多属性决策问题，利用模糊层次分析法得到评价指标属性权重的模糊区间数，根据区间数特征向量法讨论区间数排序，进而确定主要防御方向，文献［3］中将区间数转换为集对分析联系数，利用集对分析联系数选择主要防御方向。本研究拟在文献［2 -3］基础上，利用区间数比较的可能度［3-8］对此问题做进一步的分析和探讨，以期为解决其他类似问题提供参考。

1 预备知识

1.1 区间数及其运算

定义1a =［a-，a+］={x|0 ＜a-≤x≤a+} 称为一正闭区间数，简称为区间数。若a-=a+，则区间数退化为普通正实数。

设a=［a-，a+］，b=［b-，b+］，则可定义如下运算:

1)相等，a=b⇔a-=b-，a+=b+;

2)加法，a + b =［a-，a+］+［b-，b+］=［a-+ b-，a++b+］;

3)乘法，a·b =［a-，a+］·［b-，b+］=［a-b-，a+b+］。

1.2 区间数比较的可能度公式

定义2当a，b 均为实数时，称

为a ＞b 的可能度。

定义3当a，b 均为区间数或其一为区间数时，则称

为a≥b 的可能度(其中la=a+-a-，lb=b+-b-)。

定义3 也可通过以下3 个计算式定义:

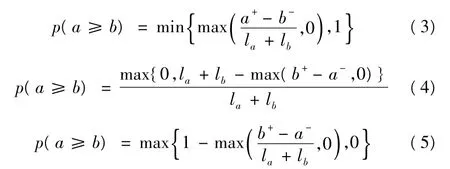
1.3 区间数排序

2 决策模型

设有方案集X ={ X1，X2，…，Xm}，指标集Y = { Y1，Y2，…，Yn}，指标权重集W = { w1，w2，…，wn}，其中方案Xi关于指标Yj的属性值xij构成决策矩阵X =(xij)m×n，其中xij=以下为决策过程:

步骤1确定规范化决策矩阵

对于效益型属性Yj

对于成本型属性Yj

步骤2求取加权规范化决策矩阵

步骤3求取各方案Xi的综合属性值zi(w)(这里，i =1，2，…，m)，

步骤4利用区间数比较的可能度计算式(2)～式(5)，计算各方案Xi的综合属性值zi(w)(这里，i=1，2，…，m)之间的可能度pij=p(zi(w)≥zj(w))(这里i =1，2，…，m; j =1，2，…，m)，建立可能度矩阵P=(pij)m×m。

步骤5利用式(6)求取可能度矩阵P =(pij)m×m的排序向量v=(v1，v2，…，vm)，按其分量大小对各方案排序，可得最优方案。

3 实证分析

仍以文献［2］中实例数据来说明本方法。某演习中，指挥部根据作战任务，结合× ×地域的实际情况，确定了4 个重点地域X1，X2，X3，X4作为备选地域。选择主要防御方向要考虑的主要属性是要符合上级意图(Y1)、本级任务(Y2)，敌方情况(Y3)，和地形条件(Y4)等4 个方面。其规范化决策矩阵及指标属性见表1［2］。

表1 决策矩阵及其指标属性

据此得到加权规范化决策矩阵

利用式(2)求得zi(w)(i =1，2，3，4)两两比较的可能度矩阵

利用式(6)求得可能度矩阵P 的排序向量

据此得到区间数zi(w)(i=1，2，3，4)的排序为

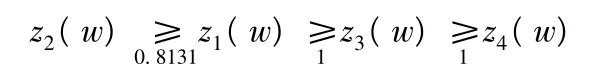
4 结论

针对属性和权重皆为区间数的有限方案多属性决策问题，利用区间数比较的可能度，给出了一种基于区间数比较的决策方法，该法所需计算量少，便于计算机实现，具有较好的适用性，可以为其他类似决问题提供参考。

［1］卢青，陈岩.陆军合同攻防战斗［D］.宣化:炮兵指挥学院，2005.

［2］宋占岭.基于区间数特征向量法(IEM)的主要防御方向选择问题［J］.兵工自动化，2009，28(4):18-20.

［3］宋占岭，王忠武，王锐.基于集对分析联系数的主要防御方向选择［J］.电子设计工程，2013，21(4):51-53.

［4］魏世孝，周献中.多属性决策理论方法及其在C3I 系统中的应用［M］.北京:国防工业出版社，1998.

［5］徐泽水.不确定多属性决策方法及其应用［M］.北京:清华大学出版社，2004.

［6］徐泽水.基于语言信息的决策理论与方法［M］.北京:科学技术出版社，2008.

［7］高峰记.可能度及区间数综合排序［J］.系统工程理论与实践，2013，33(8):2034-2042.

［8］胡明礼，范成贤，史开泉.区间数决策矩阵规范化方法的性质分析［J］.计算机科学，2013，40(10):203-208.