几何缺陷对高强钢薄壁箱形截面压杆稳定的影响

胥银华，高 磊，季珉珉，李 波

(1.总装工程兵科研二所，北京 100093; 2.解放军理工大学，南京 210007;3.江苏省南京市河西会议展览有限责任公司，南京 210019)

在钢构件制作、运输、安装等过程中都会造成构件沿长度方向出现初始挠度，通常称为整体几何缺陷。当出现整体几何缺陷后［1-3］，杆件不再是理想的直杆，对压杆整体稳定承载能力产生不可忽视的影响，因此在制定钢结构设计规范时进行了考虑。但是此规范［4］主要是针对低强度钢材(Q235 或者Q345)，随着钢结构的发展，出现了高强度［5］的钢材及其结构，但目前国内还缺乏专门针对高强钢材结构设计的规范，急需开展相关的研究。本文基于薄板的大挠度弹塑性分析理论方法［6］，利用弧长法追踪构件的荷载位移曲线以得到下降段，这样就能得到构件的极限承载能力从而进一步得到稳定系数。研究了整体几何缺陷对高强钢薄壁箱形截面压杆稳定系数的影响，得到了一些有意义的结论可供设计和使用过程中参考。

1 有限元模型的建立

基于大型有限元分析软件ANSYS12.0［7］为工作平台建立普通的有限元模型。建立了基本的有限元模型后，再将残余应力、整体几何缺陷等因素引入到模型中。模型材料选用的是18Mn2CrMoBA，通过之前对材料进行力学性能实验［8］得到其应力应变曲线，结合有限元材料模型特点提出了针对高强钢材料18Mn2CrMoBA 的多线性等向强化本构模型，如图1 所示。

图1 材料模型

为了便于施加残余应力和杆件的整体几何缺陷，在分析模型中选用壳单元(shell181)。为了模拟刚周边假定，同时为了施加约束和荷载的方便，在杆件的两端加上了两块刚性板(此板的弹性模量很大)。施加约束时，约束两边板的中央处的节点。建立的有限元基本模型如图2 所示。

图2 有限元基本模型

对于整体几何缺陷，在建立了基本模型的基础上，读取模型中所有节点的位置坐标，然后将这些节点坐标按照正弦半波形式偏移［9］，控制杆件中部的最大偏移量为设计的偏移量即可。然后按照偏移后的节点重新生成有限元模型。

对于残余应力模型选用沈祖炎［10］提出的如图3 所示的模型。取残余压应力σrc=0.1σy，受拉残余应力σrt=0.8σy。通过编制残余应力文件，然后读入残余应力的方式将其引入。将残余应力施加在单元的积分点的位置，每个shell181单元选用5 个积分点，5 个积分点沿着板厚均匀分布。由于板厚比较薄，施加残余应力时认为在5 个积分点上的大小相等，即没有考虑残余应力沿厚度方向的变化。

图3 残余应力模型

建立好有限元基本模型后利用弧长法［7］来进行求解，在求解的过程中要调整施加的荷载、采用的荷载步数和弧长半径，以确保能追踪到荷载-位移曲线的下降段。有时这一过程要反复进行才能得到满意的结果。当求解完毕后，利用后处理模块得到构件或结构的荷载位移曲线，并通过荷载位移曲线得到构件或结构的极限承载能力。输出相应的图片或者数据。

基于ANSYS 提供的APDL(ANSYS Parametric Design Language)语言［11］，根据前面所述编写了计算高强钢薄壁箱形截面压杆稳定极限承载能力的程序。程序框图如图4 所示。整个程序主要包含5 个模块:基本模型模块、引入缺陷模块、引入残余应力模块、求解模块和后处理模块。所有的程序模块都采用参数化语言，可以根据需要更改参数便于大量案例的计算。

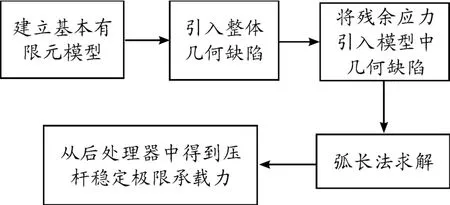
图4 稳定性计算程序框图

2 整体缺陷对高强钢薄壁箱形截面压杆稳定承载能力的影响

整体缺陷指的是构件沿长度方向出现的初始挠度。沈祖炎［10］在研究方钢管的稳定性时取整体初始挠度(杆件中部最大值)为δ/L =1/750，规范［4］容许的整体初始挠度为δ/L=1/1 000。为此在研究整体缺陷时，挠度值本文分别取δ/L=1/750、δ/L=1/1 000、δ/L =1/1 250。取模型的板厚为6 mm，翼缘和腹板的边长比值为0.6，腹板高厚比10。对不同长细比的构件进行了计算结果如表1 所示。其中Pu表示利用有限元计算得到的压杆稳定极限承载力，Py表示理论上杆件全截面屈服时的最大承载力Py=σy×A。

从表1 中的数据可以看出，虽然初始挠度最大值发生变化时，高强钢薄壁箱形截面压杆的稳定系数发生变化，但变化较小，因此对于高强钢薄壁箱形截面压杆最大初始挠度仍可参照当前规范取杆件初始挠度最大值δ/L=1/1 000。

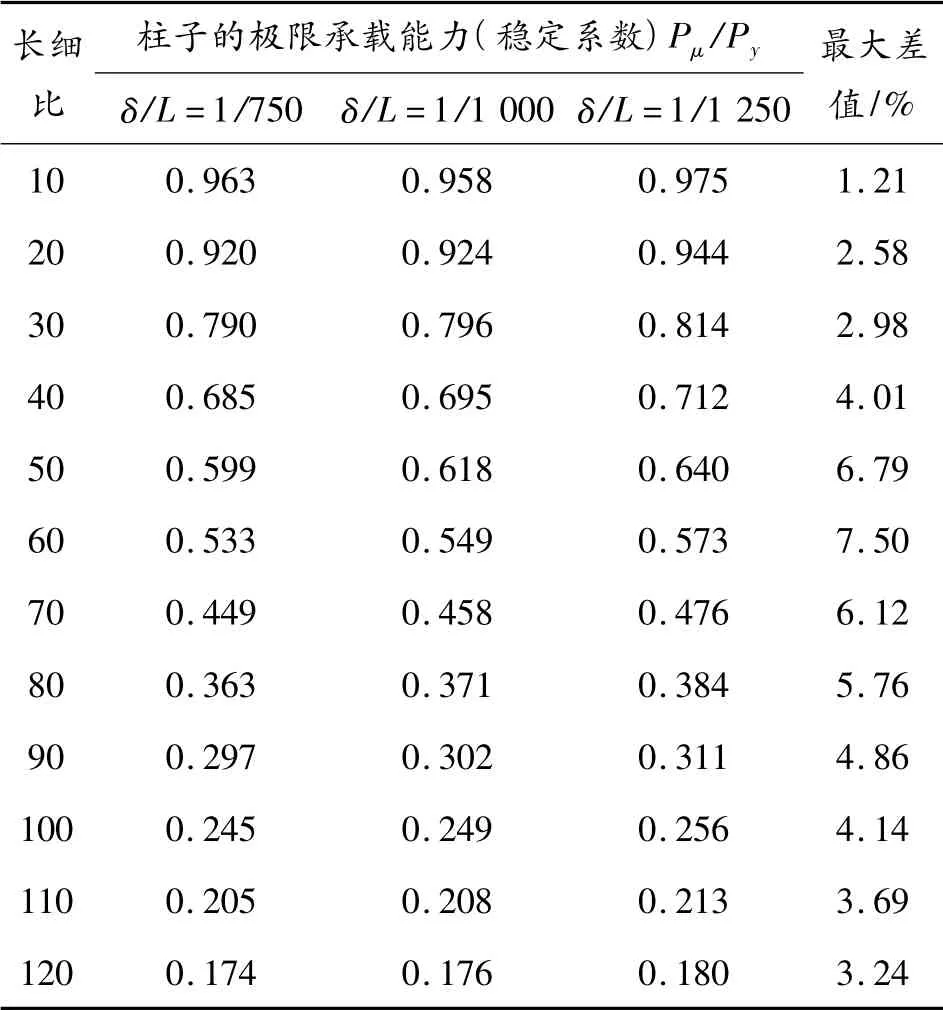
表1 不同整体初始缺陷对不同长细比构件稳定性的影响

为了研究高强钢薄壁箱形截面压杆稳定极限承载力对不同整体几何缺陷的敏感程度，将不同长细比对整体初始缺陷的敏感性通过图5 表示出来。所谓不同长细比对整体初始缺陷的敏感性是指，在同一长细比下，整体初始缺陷发生变化时构件稳定系数的变化范围。变化范围越大，说明此类长细比对整体初始缺陷敏感性强反之表示敏感性弱。从图5可以看出，整体初始缺陷对不同长细比的影响是不同的。当长细比较大或较小时，构件对整体初始缺陷的敏感性较弱，而中等长度的构件对整体初始缺陷的敏感性较强。尤其是长细比为60 附近对整体缺陷的敏感性最强，在设计和使用中应引起注意。

图5 不同长细比构件对不同整体初始缺陷的敏感性

3 结论

通过本文的研究发现，对于高强钢薄壁箱形截面压杆研究其稳定性时整体几何初始缺陷的最大值可以取杆件长度的1/1 000。同时发现不同的长细比杆件对缺陷的敏感程度不同，对于由材料18Mn2CrMoBA 制成的薄壁箱形截面压杆，当长细比为60 左右时对整体几何缺陷的敏感性最高，在设计和使用中要引起注意。

［1］王小平，汪辉，蒋沧如.考虑初始缺陷的厚壁冷弯方钢管柱承载力研究［J］. 广西工学院学报，2005，16(2):30-34.

［2］张晓霞，钟文生，姚远.初始挠度及中间弹性支撑对压杆稳定的影响分析［J］.机械，2011，38(6):1-4.

［3］常旭，张玉娇，张后全.几何缺陷影响下闭口薄壁型钢轴向受力构件力学性能研究［J］.河南理工大学学报:自然科学版，2013，32(1):93-97.

［4］GB50017—2003，钢结构设计规范［S］.

［5］苟明康，陶莉.σs≥700 MPa 的高强钢在移动桥梁装备中的应用［J］.钢结构，2002，17(5):6-8.

［6］刘宗民，梁立孚，宋海燕.弹性薄板大挠度问题两类变量的广义变分远原理［J］. 东北林业大学学报，2008，36(6):68-73.

［7］张朝晖.ANSYS12.0 结构分析工程应用实例解析［M］.北京:机械工业出版社，2009.

［8］Lei Gao，Hongcai Sun. Load-carrying capacity of highstrength steel box-sections I: Stub columns［J］. Journal of Constructional Steel Research，2009(65):918-924.

［9］王兵，胡长明，葛召深，等.考虑初始缺陷的扣件式钢管板支架极限承载力研究［J］. 西安建筑科技大学学报，2012，44(6):792-198.

［10］沈祖炎，张其林. 受压方管钢柱的屈曲后极限承载力［J］.土木工程学报，1991，24(3):15-26.

［11］博弈创作室.APDL 参数化有限元分析技术及其应用实例［M］.北京:中国水利出版社，2004.

［12］陈骥.钢结构稳定理论与设计［M］.5 版.北京:科学出版社，2011.