一种导弹捕获目标快速判断方法
李士刚,卢元磊
(1.海军驻上海地区航天系统军代室,上海 200000; 2.江苏自动化研究所,江苏连云港 222006)
用仿真手段统计导弹对目标的捕获概率是一种常用的方法[1]。仿真的过程要尽可能地反映出目标真实的捕获情况,同时又要考虑仿真算法的复杂程度。实际中影响导弹捕获目标的因素众多,如目标的动力学因素、导弹的动力学因素及环境对导弹末端制导能力的影响等[2],如果在仿真过程中将这些因素全部考虑在内,则将使得仿真过程极其复杂,甚至很难进行数学仿真[3]。一般情况下,会简化仿真模型,认为目标和导弹都按某种理论曲线航行(如直线、圆弧、抛物线等)。
1 问题描述
设导弹的导引头的视场是α ° ×β °,扫描半径为D km的一个规则多面体[5]。
对导弹捕获目标进行判断有2 类方法,第一类是仿真计算方法。在导弹导引头的每个探测周期Δt 内,计算目标和导弹的相对位置关系,算出目标相对于导弹的距离、方位角和俯仰角,然后与导弹导引头的探测性能进行比对,判断目标是否进入到导弹自导扇面。这种方法最为朴素和直观,但是在进行大量蒙特卡洛仿真时,这种方法的计算量是相当可观的[6]。
另一种判断方法是数学解析计算。相对于导弹与目标的距离和导引头的探测距离,目标的体积是可以忽略的,为了计算方便,将目标视为一个点目标[4]。解析方法需要给出导弹导引头的视场和目标点的解析表达式,然后通过解方程判断探测区域与目标点是否有交点,导引头的探测区域是三维空间中的一个运动多面体,对其进行数学解析描述是很复杂的,因此完全的数学解析方法,在实际中很难应用。
针对这种情况,本文提出了一种新的导弹捕获目标判断方法,该方法结合了仿真计算方法和数学解析的特点。下面将对其进行详细阐述。
2 导弹与目标的相对关系
相对于判断一个空间体与一个空间点的位置关系,空间中2 个运动点的位置关系判断要简单的多。基于这种想法,选取了探测区域内的2 个特殊点进行预判断。这2 个特殊点分别是导引头视场的内切圆和外接圆。
为了使描述更加清晰,目标点和导引头探测区域的剖面位置关系可参见图1 和图2 所示。
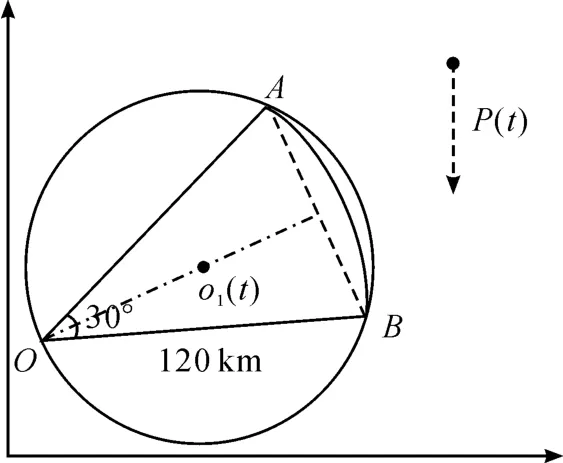
图1 导引头扫描区域外接圆示意图
扇形OAB 是导引头的探测区域的剖面示意图,球o1(t)是探测区域的外接圆,半径为r1,p(t)点表示目标点。

图2 导引头扫描区域内切圆示意图
球o2(t)是探测区域的内切圆,半径为r2。显然,球o1(t)能够完全包含导引头的探测区域,球o2(t)能完全被导引头的探测区域包含。
显然,只要目标能进入内切圆,则必定能够被导弹捕获,;只要目标不能进入外接圆,则必定不能被导弹捕获。通过该预判,可以将相当一部分的空间体与空间点的位置关系计算简化为空间中2 个点的关系判断,这将大大降低计算量,而且该方法易于实现。
3 捕获判别
假设导弹从发射到探测捕获到目标这段时间内是按照匀速直线运动飞行的;导弹打击目标往往会选择目标处于匀速运动的阶段内,因此在本文中将导弹和目标的运动状态都按照匀速直航处理。
目标位置点p(t)、导引头探测区域外接圆圆心o1(t)和内切圆圆心o2(t)都是关于时间的函数。设导弹发射的时刻为t=0,在t >0 的时间内,如果目标点p(t)与o1(t)点的最小距离大于r1,那么p(t)点肯定不能进入探测区域,即可判断捕获失败;如果p(t)与o2(t)的最小距离小于r2,那么p(t)点肯定能进入探测区域,即可判断捕获成功。
设目标位置点p(t)点的坐标为:(xp(t),yp(t),zp(t));导弹o(t)点的坐标为:(xo(t),yo(t),zo(t));外接圆心o1(t)点的坐标为:(xo1(t),yo1(t),zo1(t));内切圆圆心o2(t)的坐标为:(xo2(t),yo2(t),zo2(t))。
目标位置点p(t)点与圆心o1(t)点的距离为关于时间t的函数do1p(t)

其中,令

则有

可知外切圆圆心与目标距离的平方是关于时间t 的一元二次函数,该函数存在最小值点,当t >0 时,若该函数的最小值大于则表明目标不可能进步导弹的探测范围内,必然捕获失败;若最小值小于,则结果待定。即判断不等式是否有解

若该不等式无解,则必捕获失败;若有解,则结果待定。
目标位置点p(t)点与圆心o2(t)点的距离为关于时间t的函数do2p(t)为
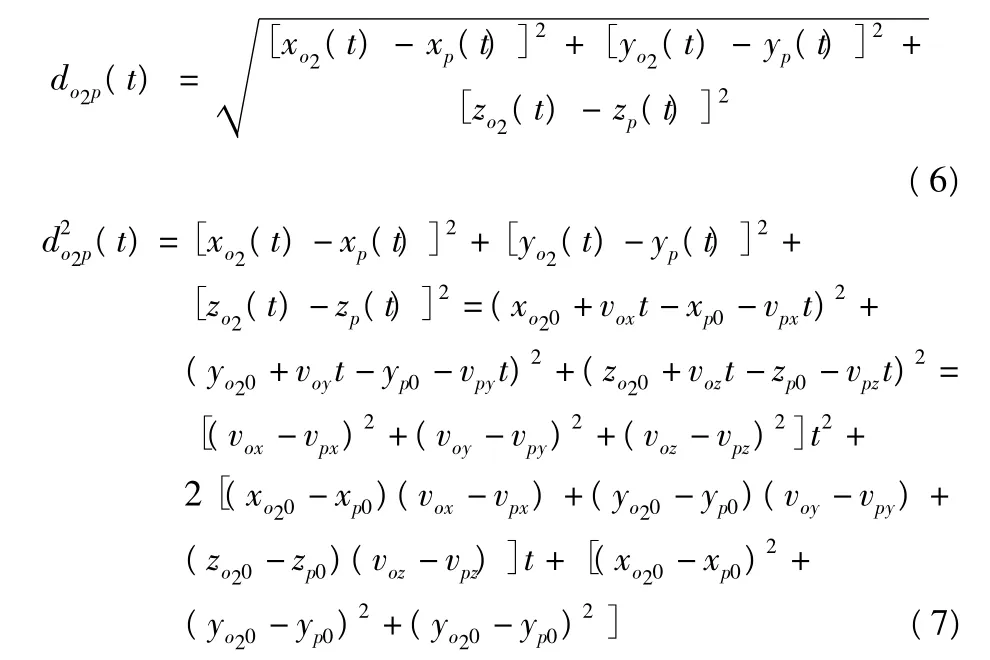
其中,令
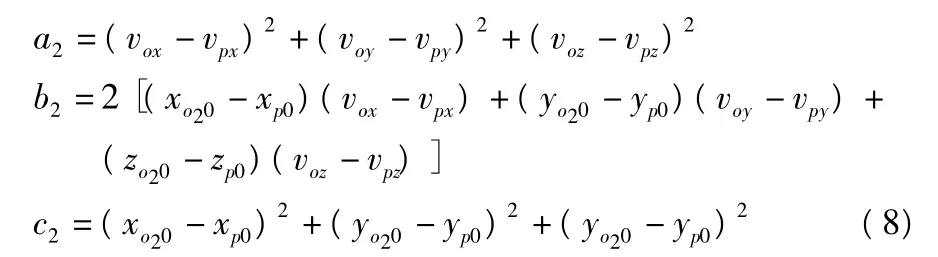
则有
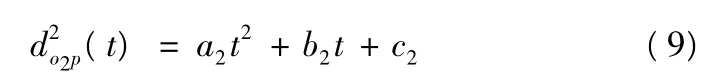
可知内切圆圆心与目标的距离函数的平方是一元二次函数,该函数存在最小值,当t >0 时,若该函数最小值小于,则目标必然会进入导弹的探测范围,捕获成功;若最小值大于则结果待定。问题即转化为判断下不等式是否有解
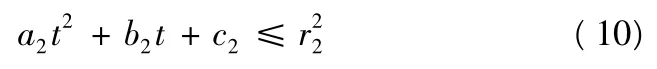
若该不等式有解,则必捕获成功;若无解,则结果待定。
综上所述,结合2 种情况,可给出如下的判别规则:
1)如果a1t2+b1t+c1≤无解,则给出结论:捕获目标失败;
2)如果a2t2+b2t+c2≤有解,则给出结论:捕获目标成功;
4 仿真分析
仿真条件设置:目标距离导弹发射点的距离为400 km,方位为0°,舷角0°,目标以9 km 的高度保持匀速巡航,航速为550 km/h。导弹发射后根据目标指示的方位和俯仰角以3 马赫的速度匀速直线飞向目标,设导弹导引头的探测距离为100 km,水平视角为60°,俯仰视角为30°,扫描周期为0.1 s,导弹发射后导引头即开机。
进行1 000 次蒙特卡洛仿真,统计结果如表1 所示。可以看出新方法统计的捕获成功概率与传统的仿真方法是基本一致的,因此新方法能有效地判别导弹能否捕获目标。
对该态势进行分析可以看出,导弹从发射到发现目标需要飞行约274 s,在这段时间内传统的仿真方法需要根据导弹和目标的相对位置进行不断地计算和判断,在单次仿真中,就需要对目标的方位角、俯仰角和相对距离进行2740 次计算和判断,而且这些计算大部分是三角函数计算,在多次仿真的情况下,其计算量是相当可观的。而新方法只结合了数学解析法的优点,首先对两个二次不等式a1t2+b1t +c1≤进行预判断,以方位误差为2°的情况为例,经过预判后共967 次仿真被一次性判断出捕获是否成功,极大地减少了仿真的计算量。

表1 捕获概率统计结果
5 结论
为了更好地处理仿真过程中导弹捕获目标的判断问题,提出了一种新的捕获判断方法,新方法结合了仿真计算方法和数学解析方法的特点。通过仿真结果可以看出新方法是有效的,而且具有简单易用的优点,且有效减少了仿真计算的次数。这里需要说明的是这种新方法可应用于多种末制导导弹的目标捕获仿真判断,而且目标的运动形式并不仅仅限于匀速直线运动。
[1]张亚,孔军. 潜射巡航导弹现在点攻击捕获概率计算[J].指挥控制与仿真,2010(2):40-42.
[2]魏海光,边聚广.一种反舰导弹纯方位攻击捕获概率计算方法[J].四川兵工学报,2012(3):22-25.
[3]常皓,徐文旭,齐占元.导弹作战过程误差传递及末制导捕获概率分析[J].弹箭与制导学报,2008(3):81-84.
[4]陈力,张树森,李军林.反舰导弹目标捕捉概率影响因素分析[J].火力与指挥控制,2011(6):86-88.
[5]刘环宇.精确解算舰舰导弹捕捉概率的数值算法[J].战术导弹技术,2001(6):23-27.
[6]王涛,旷志高,李晓阳.目标散布下反舰导弹捕捉概率的计算[J].火力与指挥控制,2003(21):77-78.

