让数学课堂焕发出思维的活力

北京市黄冈中学垡头校区 魏红艳

苏联著名教育家斯托利亚尔在《数学教育学》一书中指出：“数学教学是数学活动的教学（思维活动的教学）。”在教育改革的今天，我们数学教师应力所能及地致力于将数学教学变为思维活动的教学的研究。近几年，我在学习他人优秀经验的基础上，不断地进行探索和实践。我认为，要将数学课堂变为培养学生思维的阵地，不妨采取以下几点做法。

一、开放教学环境，创设民主平等的教学氛围，给学生留有表达思维的时间

在压抑的思想环境下，禁锢的课堂氛围中,是不可能产生创造性思维火花的。因此，教学中，教师的首要任务是营造一种生动活泼、民主平等的教学气氛，使学生敢于参与、思维活跃、富有创造性。

二、恰当运用多种教学方法，激发学生兴趣，提高学生参与的观能动性

（一）“活”用教材,巧设问题情境，激发学生兴趣

教学情境是学生掌握知识、形成能力、发展思维品质的重要源泉，是沟通现实生活与数学学习、具体问题与抽象概念之间的桥梁。精心创设各种教学情境，将学习活动置于社会生活问题之中，能够激发学生的学习动机和好奇心，培养学生的求知欲望，引导学生主动积极地获取知识，从而形成良好思维品质。

（二）运用变式教学，保持学生参与教学活动的热情

变式教学是对数学中的定理和命题进行不同角度、不同层次、不同情形、不同背景的变式，以暴露问题的本质特征，揭示不同知识点间的内在联系的一种教学设计方法。通过变式教学，使一题多用，多题重组，常给人以新鲜感，能唤起学生的好奇心和求知欲，从而保持其参与教学过程的热情。

三、合理运用现代化信息技术，使数学课堂教学直观化、灵动化，帮助学生突破思维障碍点

现代教育技术理论认为，要全面实施素质教育，传统教学陈旧的教学手段和简单的教学技术在当今世界的多层次教学、演示教学、实验教学等现代化课堂教学中就显得力不从心。计算机多媒体教学可以创设开放式的教学情景，使得教学情趣盈然、丰富多彩，符合青少年学生年龄特征和心理需要。例如，在一节“抛物线的再认识”的课堂教学中，一位老师就巧妙地运用几何画板的“动画”及“追踪”功能，突破学生的思维难点，赢来学生的一片惊讶赞叹之声。具体情境如下。

首先，老师创设这样一个问题情境：在一片草原上有一个蒙古包和一条树林带，欲修一个观景亭，使得观景亭到蒙古包和树林带的距离相等，你觉得观景亭建在哪里合适？然后，师生互动，顺利地将此实际问题转化为数学问题：设点A为蒙古包，直线l为树林带，求作观景亭点P，使点P与点A和直线l的距离相等。

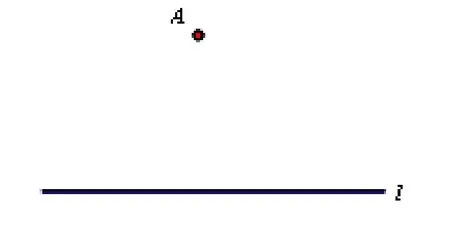
并得出如下三种解法。

方法1：如图1，在l上任取一点M，过M作l的垂线k，连接AM， AM的垂直平分线与k的交点即为点P。

方法2：如图2，在l上任取一点M，连接AM，过A作AM的垂线与∠AMB的角平分线的交点即为点P。

方法3：如图3，在l外任取一点M，过M作直线n∥l，作MN⊥l于点N，然后以A为圆心，以MN长为半径画弧与n的交点即为点P。

接着，老师将问题升级，提出：在以上画法中，点M选取位置不同，点P的位置就不同，即满足条件的点P有很多，那我们干脆设计一条观景长廊，使观景人无论走到观景长廊的任何位置，到蒙古包与树林带的距离都相等，同学们探索一下这个观景长廊会是怎样的图形，如何建呢？请任选其中一种画法进行尝试，多画几个点P观察猜想一下。

学生兴趣盎然，快速动笔。程度较好的学生很快地，通过画出多个点P，发现点P的集合貌似是一条抛物线，而程度弱一些的学生随着画图中线条的增多，完成出现困难。为了帮助学生解惑，老师首先展示一些学生的优秀作品，给学生树立勇于探索的榜样，然后运用计算机几何画板软件进行动态演示——让的点M动起来的同时，对点P位置进行追踪，一条由点P汇聚而成的抛物线清晰地展现在同学们面前。

突入其来的直观冲击，引来学生一片惊讶赞叹之声。稍慢一些的学生困惑得释，同学们达成共识：猜想“点P的集合是一条抛物线”,教学继续进入论证环节。

四、采用多样的评价方式，促进学生思维的碰撞

不妨让学生评价学生

课堂上，总是教师评价学生，往往不能保证学生参与的深度和广度，所以，在学生展示交流的环节，我常引导学生从结果和解题思路等方面相互评价,这样，既给学生搭建了展示的平台，又有利于学生的充分交流。

(二)多尺度评价学生

新课标指出，评价既要关注学生学习的结果，也要重视学生学习的过程；既要关注学生数学学习的水平，也要重视学生在数学活动中所表现出来的情感与态度。所以课堂上，我经常采取多元积分的评价方式，从学生回答问题声音洪亮度，思维清晰度、能否提出有价值的新问题，板演是否工整规范等方面多角度评价。从而有效地提高了学生参与度。

(三)采用小组捆绑式评价

目前，小组合作已成为倍受青睐的课堂教学方式。那么我想，我们的评价方式也应随之更新。我采用了小组捆绑式评价，即将课堂上每一个学生的表现加分纳入其所在小组的得分,定期给予得分最高的优胜组以整体奖励。在这样的评价方式下，每一名学生都抱着力争为小组争光的心态积极参与课堂，学生在相互合作中实现了共赢。

总之， 课堂是我们进行教学的主阵地，要锻炼学生的思维，提升学生的能力，我们必须倾注全力打造学生乐于参与、乐于思索、乐于合作、乐于收获的课堂，长此以往，我们才能让数学课堂焕发出应有的思维活力。