关于Euler函数一个方程的正整数解

张四保，刘启宽

（1.喀什大学数学与统计学院，新疆喀什844008；2.昆明学院数学系，云南昆明650214）

关于Euler函数一个方程的正整数解

张四保1，刘启宽2

（1.喀什大学数学与统计学院，新疆喀什844008；2.昆明学院数学系，云南昆明650214）

研究了方程φ（abc）＝6（φ（a）＋φ（b）＋φ（c））的可解性问题，利用初等方法给出了该方程所有的204组正整数解，其中φ（n）为Euler函数.

Euler函数；不定方程；正整数解

0 引言

不定方程是数论中的一个重要内容，其研究范围十分广泛，如文献［1］就研究了一类方程的正整数解问题.Euler函数φ（n）的值等于序列0，1，2，…，n－1中与n互素的整数的个数.关于φ（n）方程的研究是初等数论中非常有意义的课题［2］.文献［3-4］讨论了φ（φ（n））＝2ω（n）的可解性问题；文献［5］探讨了φ（x1…xk）＝φ（x1）＋…＋φ（xk）的可解性；文献［6］探讨了φ（n2）＝2ω（n2）的可解性；文献［7］探讨了φ（x）＝S（x3）的可解性，其中S（x）为Smarandache函数；文献［8］运用初等方法讨论了方程φ（n）的可解性；文献［9］讨论了方程φ（abc）＝2（φ（a）＋φ（b）＋φ（c））的可解性，并给出其全部正整数解.本文将讨论方程φ（abc）＝6（φ（a）＋φ（b）＋φ（c））的可解性，给出了如下结论：

定理 不定方程

有正整数解（a，b，c）＝（49，1，7），（98，1，7），（49，1，14），（49，2，7），（15，3，3），（24，3，3），（30，3，3），（26，3，4），（28，3，4），（12，3，4），（6，3，6），（8，3，6），（10，3，6），（15，3，6），（26，4，3），（28，4，3），（12，4，3），（13，4，4），（21，4，4），（13，4，6），（6，6，3），（8，6，3），（10，6，3），（15，6，3），（13，6，4），（5，6，6），（3，6，6），（49，7，1），（98，7，1），（49，7，2），（49，14，1），（19，3，5），（38，3，5），（9，3，5），（18，3，5），（19，3，10），（9，3，10），（6，3，10），（19，3，8），（9，3，8），（6，3，8），（7，3，12），（4，3，12），（19，4，5），（27，4，5），（3，4，12），（19，6，5），（9，6，5），（6，6，5），（3，6，10），（3，6，8），（19，5，3），（38，5，3），（9，5，3），（18，5，3），（19，10，3），（9，10，3），（6，10，3），（19，8，3），（9，8，3），（6，8，3），（7，12，3），（4，12，3），（19，5，4），（27，5，4），（3，12，4），（19，5，6），（9，5，6），（6，5，6），（3，10，6），（3，8，6），（20，3，7），（16，3，7），（7，3，7），（14，3，7），（12，3，7），（5，3，9），（10，3，9），（8，3，9），（7，3，14），（5，3，18），（15，4，7），（9，4，7），（7，4，9），（7，6，7），（5，6，9），（20，7，3），（16，7，3），（7，7，3），（14，7，3），（12，7，3），（5，9，3），（10，9，3），（8，9，3），（7，14，3），（5，18，3），（15，7，4），（9，7，4），（7，9，4），（7，7，6），（5，9，6），（7，3，20），（7，3，16），（3，3，15），（3，3，24），（3，3，30），（3，6，15），（6，3，15），（7，20，3），（7，16，3），（3，15，3），（3，24，3），（3，30，3），（3，15，6），（6，15，3），（3，4，26），（4，3，26），（3，4，28），（4，3，28），（4，4，13），（4，4，21），（4，6，13），（6，4，13），（3，26，4），（4，26，3），（3，28，4），（4，28，3），（4，13，4），（4，21，4），（4，13，6），（6，13，4），（3，5，9），（3，10，9），（3，5，18），（3，8，9），（3，12，7），（6，5，9），（3，9，5），（3，9，10），（3，18，5），（3，9，8），（3，7，12），（6，9，5），（1，7，49），（1，7，98），（1，14，49），（2，7，49），（1，49，7），（1，98，7），（1，49，14），（2，49，7），（3，5，19），（3，5，38），（3，19，5），（3，38，5），（4，5，19），（4，5，27），（4，19，5），（4，27，5），（6，5，19），（6，19，5），（3，8，19），（3，19，8），（3，10，19），（3，19，10），（3，7，7），（3，7，14），（3，14，7），（4，7，7），（6，7，7），（4，7，9），（4，9，7），（3，7，20），（3，20，7），（3，7，16），（3，16，7），（4，7，15），（4，15，7），（5，3，19），（5，3，38），（5，19，3），（5，38，3），（5，4，19），（5，4，27），（5，19，4），（5，27，4），（5，6，19），（5，19，6），（8，3，19），（8，19，3），（10，3，19），（10，19，3），（7，1，49），（7，1，98），（14，1，49），（7，2，49），（7，49，1），（7，98，1），（14，49，1），（7，49，2），（7，7，4），（7，4，7），（7，4，15），（7，15，4）.

1 主要引理

引理1［10］对任意正整数n与m

引理2［10］当n≥2是整数时，φ（n）＜n；当n≥3是整数时，φ（n）为偶数.

引理3［9］对任意正整数n，p为素数，若（n，p）＝1，则φ（np）＝（p－1）φ（n）；若（n，p）＝p，则φ（np）＝pφ（n）.

引理4［11］方程φ（x）＝2P的解x为：当P＝2时，x＝5，8，10，12.当P＝3时，x＝7，9，14，18.当P≥5时，若g＝2P＋1为素数，则方程φ（x）＝2P有两个解x＝g，2g；若g＝2P＋1不为素数，则方程φ（x）＝2P无正整数解.

引理5［11］（1）当q＝2p＋1，且2pq＋1为素数时，方程φ（x）＝2pq的解为x＝q，q2，2pq＋1，2（2pq＋1）；（2）当q＝2p＋1，但2pq＋1不为素数时，方程φ（x）＝2pq的解为x＝q，2q2；（3）当q≠2p＋1，但2pq＋1为素数时，方程φ（x）＝2pq的解为x＝2pq＋1，2（2pq＋1）；（4）其他情形，方程φ（x）＝2pq无解，其中p，q是满足q＞p＞2的素数.

2 定理证明

由于φ（abc）＝6（φ（a）＋φ（b）＋φ（c）），则有

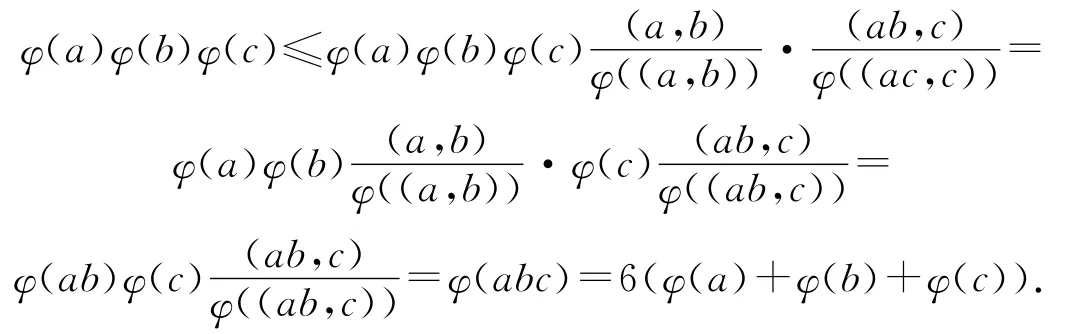
从而有

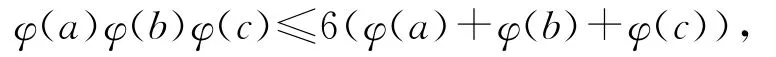
即

下面将φ（b）φ（c）值分两种情况分别加以讨论：

情况1 φ（b）φ（c）≤6.

当φ（b）φ（c）≤6时，有（b，c）＝（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（1，7），（1，8），（1，9），（1，10），（1，12），（1，14），（1，18），（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），（2，7），（2，8），（2，9），（2，10），（2，12），（2，14），（2，18），（3，1），（3，2），（3，3），（3，4），（3，6），（4，1），（4，2），（4，3），（4，4），（4，6），（5，1），（5，2），（6，1），（6，2），（6，3），（6，4），（6，6），（7，1），（7，2），（8，1），（8，2），（9，1），（9，2），（10，1），（10，2），（12，1），（12，2），（14，1），（14，2），（18，1），（18，2）.

将以上（b，c）的可能值代入方程（1），结合以上所给的引理可得，方程（1）有正整数解（a，b，c）＝（49，1，7），（98，1，7），（49，1，14），（49，2，7），（15，3，3），（24，3，3），（30，3，3），（26，3，4），（28，3，4），（12，3，4），（6，3，6），（8，3，6），（10，3，6），（15，3，6），（26，4，3），（28，4，3），（12，4，3），（13，4，4），（21，4，4），（13，4，6），（6，6，3），（8，6，3），（10，6，3），（15，6，3），（13，6，4），（5，6，6），（3，6，6），（49，7，1），（98，7，1），（49，7，2），（49，14，1）.

情况2 φ（b）φ（c）＞6.

情况2.1 当φ（b）φ（c）＝8时，有：φ（b）＝1，φ（c）＝8或φ（b）＝2，φ（c）＝4或φ（b）＝4，φ（c）＝2或φ（b）＝8，φ（c）＝1.

当φ（b）＝1，φ（c）＝8时，有b＝1，2；c＝15，16，20，24，30.此时，当（b，c）＝（1，15）时，有φ（15a）＝6φ（a）＋54.而当（a，15）＝1时，φ（15a）＝8φ（a）；当（a，15）＝3时，φ（15a）＝12φ（a）；当（a，15）＝5时，φ（15a）＝10φ（a）；当（a，15）＝15时，φ（15a）＝15φ（a）.因而，方程（1）无正整数解.仿（b，c）＝（1，15）的讨论可得，对于b与c的所有组合，方程（1）无正整数解.由此可知，当φ（b）＝1，φ（c）＝8与φ（b）＝8，φ（c）＝1时，方程（1）无正整数解.

当φ（b）＝2，φ（c）＝4时，有：b＝3，4，6；c＝5，10，8，12.此时，当（b，c）＝（3，5）时，方程（1）有正整数解（a，b，c）＝（19，3，5），（38，3，5），（9，3，5），（18，3，5）；当（b，c）＝（3，10）时，方程（1）有正整数解（a，b，c）＝（19，3，10），（9，3，10），（6，3，10）；当（b，c）＝（3，8）时，方程（1）有正整数解（a，b，c）＝（19，3，8），（9，3，8），（6，3，8）；当（b，c）＝（3，12）时，方程（1）有正整数解（a，b，c）＝（7，3，12），（4，3，12）；当（b，c）＝（4，5）时，方程（1）有正整数解（a，b，c）＝（19，4，5），（27，4，5）；当（b，c）＝（4，12）时，方程（1）有正整数解（a，b，c）＝（3，4，12）；当（b，c）＝（6，5）时，方程（1）有正整数解（a，b，c）＝（19，6，5），（9，6，5），（6，6，5）；当（b，c）＝（6，10）时，方程（1）有正整数解（a，b，c）＝（3，6，10）；当（b，c）＝（6，8）时，方程（1）有正整数解（a，b，c）＝（3，6，8）；而其余情况均无正整数解.

由此可得，当φ（b）＝4，φ（c）＝2时，方程（1）有正整数解（a，b，c）＝（19，5，3），（38，5，3），（9，5，3），（18，5，3），（19，10，3），（9，10，3），（6，10，3），（19，8，3），（9，8，3），（6，8，3），（7，12，3），（4，12，3），（19，5，4），（27，5，4），（3，12，4），（19，5，6），（9，5，6），（6，5，6），（3，10，6），（3，8，6）.

情况2.2 当φ（b）φ（c）＝10时，有φ（b）＝1，φ（c）＝10或φ（b）＝10，φ（c）＝1.

当φ（b）＝1，φ（c）＝10时，有：b＝1，2；c＝11，22.仿φ（b）φ（c）＝8情况的讨论可得，此时方程（1）无正整数解.从而，当φ（b）φ（c）＝10时，方程（1）无正整数解.

情况2.3 当φ（b）φ（c）＝12时，有φ（b）＝1，φ（c）＝12或φ（b）＝2，φ（c）＝6或φ（b）＝6，φ（c）＝2或φ（b）＝12，φ（c）＝1.

当φ（b）＝1，φ（c）＝12时，有：b＝1，2；c＝13，21，26，28，36，42.此时，方程（1）无正整数解.

当φ（b）＝2，φ（c）＝6时，有：b＝3，4，6；c＝7，9，14，18.此时，当（b，c）＝（3，7）时，方程（1）有正整数解（a，b，c）＝（20，3，7），（16，3，7），（7，3，7），（14，3，7），（12，3，7）；当（b，c）＝（3，9）时，方程（1）有正整数解（a，b，c）＝（5，3，9），（10，3，9），（8，3，9）；当（b，c）＝（3，14）时，方程（1）有正整数解（a，b，c）＝（7，3，14）；当（b，c）＝（3，18）时，方程（1）有正整数解（a，b，c）＝（5，3，18）；当（b，c）＝（4，7）时，方程（1）有正整数解（a，b，c）＝（15，4，7），（9，4，7）；当（b，c）＝（4，9）时，方程（1）有正整数解（a，b，c）＝（7，4，9）；当（b，c）＝（6，7）时，方程（1）有正整数解（a，b，c）＝（7，6，7）；当（b，c）＝（6，9）时，方程（1）有正整数解（a，b，c）＝（5，6，9）；而其余情况均无正整数解.

从而，此时方程（1）有正整数解（a，b，c）＝（20，3，7），（16，3，7），（7，3，7），（14，3，7），（12，3，7），（5，3，9），（10，3，9），（8，3，9），（7，3，14），（5，3，18），（15，4，7），（9，4，7），（7，4，9），（7，6，7），（5，6，9），（20，7，3），（16，7，3），（7，7，3），（14，7，3），（12，7，3），（5，9，3），（10，9，3），（8，9，3），（7，14，3），（5，18，3），（15，7，4），（9，7，4），（7，9，4），（7，7，6），（5，9，6）.

情况2.4 当φ（b）φ（c）＝14时，有φ（b）＝1，φ（c）＝14或φ（b）＝14，φ（c）＝1.

根据引理4可知，φ（b）＝14无正整数解，因而，此时方程（1）无正整数解.

情况2.5 当φ（b）φ（c）＝16时，有φ（b）＝1，φ（c）＝16或φ（b）＝2，φ（c）＝8或φ（b）＝4，φ（c）＝4或φ（b）＝8，φ（c）＝2或φ（b）＝16，φ（c）＝1.

当φ（b）＝1，φ（c）＝16时，有：b＝1，2；c＝17，34，60，40，32，48.此时，方程（1）无正整数解.

当φ（b）＝2，φ（c）＝8时，有：b＝3，4，6；c＝15，30，20，16，24.此时，方程（1）有正整数解（a，b，c）＝（7，3，20），（7，3，16），（3，3，15），（3，3，24），（3，3，30），（3，6，15），（6，3，15）.

因而，此时方程（1）有正整数解（a，b，c）＝（7，3，20），（7，3，16），（3，3，15），（3，3，24），（3，3，30），（3，6，15），（6，3，15），（7，20，3），（7，16，3），（3，15，3），（3，24，3），（3，30，3），（3，15，6），（6，15，3）.

当φ（b）＝4，φ（c）＝4时，有b＝c＝5，8，10，12.此时，方程（1）无正整数解.

情况2.6 当φ（b）φ（c）＝18时，有φ（b）＝1，φ（c）＝18或φ（b）＝18，φ（c）＝1.

当φ（b）＝1，φ（c）＝18时，有：b＝1，2；c＝27，54，19，38.此时，方程（1）无正整数解.

情况2.7 当φ（b）φ（c）＝20时，有φ（b）＝1，φ（c）＝20或φ（b）＝2，φ（c）＝10或φ（b）＝10，φ（c）＝2或φ（b）＝20，φ（c）＝1.经计算可知，此时方程（1）无正整数解.

情况2.8 当φ（b）φ（c）＝22时，有φ（b）＝1，φ（c）＝22或φ（b）＝22，φ（c）＝1.

当φ（b）＝1，φ（c）＝22时，有：b＝1，2；c＝23，46.此时，方程（1）无正整数解.

情况2.9 当φ（b）φ（c）＝24时，有φ（b）＝1，φ（c）＝24或φ（b）＝2，φ（c）＝12或φ（b）＝4，φ（c）＝6或φ（b）＝6，φ（c）＝4或φ（b）＝12，φ（c）＝2或φ（b）＝24，φ（c）＝1.

经计算，当φ（b）＝1，φ（c）＝24时，方程（1）无正整数解；当φ（b）＝2，φ（c）＝12时，方程（1）有正整数解（a，b，c）＝（3，4，26），（4，3，26），（3，4，28），（4，3，28），（4，4，13），（4，4，21），（4，6，13），（6，4，13）；当φ（b）＝4，φ（c）＝6时，方程（1）有正整数解（a，b，c）＝（3，5，9），（3，10，9），（3，5，18），（3，8，9），（3，12，7），（6，5，9）.

因而，此时方程（1）有正整数解（a，b，c）＝（3，4，26），（4，3，26），（3，4，28），（4，3，28），（4，4，13），（4，4，21），（4，6，13），（6，4，13），（3，26，4），（4，26，3），（3，28，4），（4，28，3），（4，13，4），（4，21，4），（4，13，6），（6，13，4），（3，5，9），（3，10，9），（3，5，18），（3，8，9），（3，12，7），（6，5，9），（3，9，5），（3，9，10），（3，18，5），（3，9，8），（3，7，12），（6，9，5）.

情况2.10 当φ（b）φ（c）＝26时，有φ（b）＝1，φ（c）＝26或φ（b）＝26，φ（c）＝1.

由引理4可知，φ（c）＝26无正整数解，因而此时，方程（1）无正整数解.

情况2.11 当φ（b）φ（c）≥28时，由于φ（b），φ（c）均为正整数，所以有（φ（b）－1）（φ（c）－1）≥0，即φ（b）φ（c）＋1≥φ（b）＋φ（c）.由方程（1）有

所以，φ（a）＝1，2，4，6.

情况2.11.1 若φ（a）＝1时，方程（1）可化为

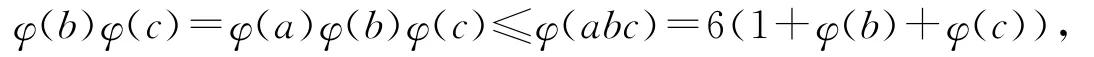
于是有

当（φ（b）－6）（φ（c）－6）＜0时，若φ（b）＝1，2，4，则φ（c）＞6.此时，有φ（a）＝φ（b）＝1或φ（a）＝1，φ（b）＝2或φ（a）＝1，φ（b）＝4.根据情况1中有关φ（b）φ（c）≤6的讨论可知，此时方程（1）无正整数解.同理，当φ（c）＝1，2，4和φ（a）＞6时，方程（1）无正整数解.

当（φ（b）－6）（φ（c）－6）≥0时，此时有（φ（b）－6）（φ（c）－6）＝0，1，2，…，42.

当（φ（b）－6）（φ（c）－6）＝0时，φ（b），φ（c）至少有一个等于6.根据情况1中有关φ（b）φ（c）≤6的讨论可知，此时方程（1）有正整数解（a，b，c）＝（1，7，49），（1，7，98），（1，14，49），（2，7，49），（1，49，7），（1，98，7），（1，49，14），（2，49，7）.

根据引理2可得，当（φ（b）－6）（φ（c）－6）＝1，2，3，5，6，7，9，10，11，13，14，15，17，18，19，21，22，23，25，26，27，29，30，31，33，34，35，37，38，39，41，42时，φ（b），φ（c）中至少有一个为奇数，因而只需考虑（φ（b）－6）（φ（c）－6）＝4，8，12，16，20，24，28，32，36，40的情形.

当（φ（b）－6）（φ（c）－6）＝4时，有φ（b）＝φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝8时，有φ（b）＝8，φ（c）＝10或φ（b）＝10，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝12时，有φ（b）＝8，φ（c）＝12或φ（b）＝12，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝20时，有φ（b）＝8，φ（c）＝16或φ（b）＝16，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝24时，有φ（b）＝8，φ（c）＝18或φ（b）＝18，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝28时，有φ（b）＝8，φ（c）＝20或φ（b）＝20，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝32时，有φ（b）＝8，φ（c）＝22或φ（b）＝22，φ（c）＝8；当（φ（b）－6）（φ（c）－6）＝36时，有φ（b）＝8，φ（c）＝24或φ（b）＝24，φ（c）＝8.由此可知，当（φ（b）－6）（φ（c）－6）＝4，8，12，20，24，28，32，36时，有φ（b）＝8或φ（c）＝8，那么可以通过讨论φ（a）＝1且φ（b）＝8来确定方程（1）是否有解.当φ（a）＝1，φ（b）＝8时，有：a＝1，2；b＝15，16，20，24，30.此时，方程（1）无正整数解.

当（φ（b）－6）（φ（c）－6）＝16时，有φ（b）＝φ（c）＝10；当（φ（b）－6）（φ（c）－6）＝24时，有φ（b）＝10，φ（c）＝12或φ（b）＝12，φ（c）＝10；当（φ（b）－6）（φ（c）－6）＝40时，有φ（b）＝10，φ（c）＝16或φ（b）＝16，φ（c）＝10.在这些情况中，可通过讨论φ（a）＝1，φ（b）＝10的情形来确定方程（1）是否有解.当φ（a）＝1，φ（b）＝10时，有a＝1，2；b＝11，22.此时，方程（1）无正整数解.

情况2.11.2 若φ（a）＝2时，方程（1）可化为

于是有

当（φ（b）－3）（φ（c）－3）＜0时，若φ（b）＝1，则φ（c）≥4，此时有a＝3，4，6；b＝1，2.根据情况1中有关φ（b）φ（c）≤6的讨论可知，此时方程（1）无正整数解.同理，当φ（c）＝1，φ（b）≥4时，方程（1）无正整数解.

当（φ（b）－3）（φ（c）－3）＝0时，φ（b），φ（c）中至少有一个等于3.由引理2可知，方程φ（b）＝3无正整数解，因而，此时方程（1）无正整数解.

当（φ（b）－3）（φ（c）－3）＝1时，有φ（b）＝φ（c）＝4或φ（b）＝φ（c）＝2.当φ（b）＝φ（c）＝4时，方程（1）无正整数解；当φ（b）＝φ（c）＝2时，方程（1）有正整数解（a，b，c）＝（6，3，6），（6，6，3），（3，6，6）.

当（φ（b）－3）（φ（c）－3）＝2，4，6，8，10，12，14时，φ（b），φ（c）中至少有一个为奇数，因而此时方程（1）无正整数解，只需讨论（φ（b）－3）（φ（c）－3）＝3，5，7，9，11，13，15的情形.

当（φ（b）－3）（φ（c）－3）＝11时，有φ（b）＝4，φ（c）＝14或φ（b）＝14，φ（c）＝4.由引理4可知，方程φ（x）＝14无正整数解，因而此时方程（1）无正整数解.

除去当（φ（b）－3）（φ（c）－3）＝9中的φ（b）＝φ（c）＝6与当（φ（b）－3）（φ（c）－3）＝15中的φ（b）＝6，φ（c）＝8或φ（b）＝8，φ（c）＝6的情况之外，在（φ（b）－3）（φ（c）－3）＝3，5，7，9，11，13，15的情形中都有φ（x）＝4这样的式子，结合φ（a）＝2的情况，只需讨论φ（a）＝2，φ（b）＝4的情况来决定方程（1）是否有正整数解.当φ（a）＝2，φ（b）＝4时，有a＝3，4，6；b＝5，8，10，12.因而，方程（1）有正整数解（a，b，c）＝（3，5，9），（3，5，18），（3，9，5），（3，18，5），（6，5，9），（6，9，5），（3，8，9），（3，9，8），（3，5，19），（3，5，38），（3，19，5），（3，38，5），（4，5，19），（4，5，27），（4，19，5），（4，27，5），（6，5，19），（6，19，5），（3，8，19），（3，19，8），（3，10，19），（3，19，10）.

在当（φ（b）－3）（φ（c）－3）＝9时，φ（b）＝φ（c）＝6与当（φ（b）－3）（φ（c）－3）＝15时，φ（b）＝6，φ（c）＝8或φ（b）＝8，φ（c）＝6这些情况下，都有φ（x）＝6，结合φ（a）＝2，讨论φ（a）＝2，φ（b）＝6的情况来决定方程（1）是否有正整数解.当φ（a）＝2，φ（b）＝6时，有：a＝3，4，6；b＝7，9，14，18.因而，方程（1）有正整数解（a，b，c）＝（3，7，7），（3，7，14），（3，14，7），（4，7，7），（6，7，7），（4，7，9），（4，9，7），（3，7，20），（3，20，7），（3，7，16），（3，16，7），（4，7，15），（4，15，7）.

情况2.11.3 若φ（a）＝4时，方程（1）可化为

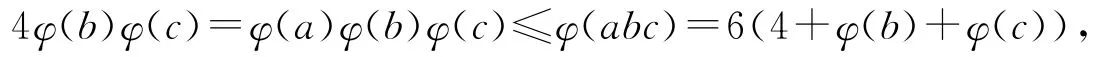
于是有

当（2φ（b）－3）（2φ（c）－3）＜0时，有φ（b）＝1，φ（c）≥2或φ（b）≥2，φ（c）＝1.根据情况1中有关φ（b）φ（c）≤6的讨论可知，此时方程（1）无正整数解.

当（2φ（b）－3）（2φ（c）－3）＝1时，有φ（b）＝φ（c）＝1或φ（b）＝φ（c）＝2.根据情况1中有关φ（b）φ（c）≤6的讨论可知，当φ（b）＝φ（c）＝1时，方程（1）无正整数解；而当φ（b）＝φ（c）＝2时，方程（1）有正整数解（a，b，c）＝（5，6，6），（8，3，6），（8，6，3），（10，3，6），（10，6，3），（12，3，4），（12，4，3）.

当（2φ（b）－3）（2φ（c）－3）＝2，3，4，6，7，8，10，11，12，14，15，16，18，19，20，22，23，24，26，27，28，30，31，32时，方程（1）无正整数解.

当（2φ（b）－3）（2φ（c）－3）＝25时，有φ（b）＝2，φ（c）＝14或φ（b）＝14，φ（c）＝2或φ（b）＝φ（c）＝4.由于方程φ（x）＝14无正整数解，因而只需讨论φ（b）＝φ（c）＝4的情形.

当（2φ（b）－3）（2φ（c）－3）＝5，9，13，17，21，29，33时，都有（b）＝2或φ（c）＝2这一关系式，结合φ（a）＝4，方程（1）有正整数解（a，b，c）＝（5，3，9），（5，3，18），（5，9，3），（5，18，3），（5，6，9），（5，9，6），（8，3，9），（8，9，3），（5，3，19），（5，3，38），（5，19，3），（5，38，3），（5，4，19），（5，4，27），（5，19，4），（5，27，4），（5，6，19），（5，19，6），（8，3，19），（8，19，3），（10，3，19），（10，19，3）.

当（2φ（b）－3）（2φ（c）－3）＝25时，有φ（b）＝φ（c）＝4.此时，方程（1）无正整数解.

情况2.11.4 若φ（a）＝6时，方程（1）可化为

于是有

当（φ（b）－1）（φ（c）－1）＝0时，有φ（b）＝1或φ（c）＝1.根据情况1中有关φ（b）φ（c）≤6的讨论可知，此时方程（1）有正整数解（a，b，c）＝（7，1，49），（7，1，98），（14，1，49），（7，2，49），（7，49，1），（7，98，1），（14，49，1），（7，49，2）.

当（φ（b）－1）（φ（c）－1）＝2，4，6时，φ（b），φ（c）中至少有一个不成立，方程（1）无正整数解.

当（φ（b）－1）（φ（c）－1）＝1时，有φ（b）＝φ（c）＝2；当（φ（b）－1）（φ（c）－1）＝3时，有φ（b）＝2，φ（c）＝4或φ（b）＝4，φ（c）＝2；当（φ（b）－1）（φ（c）－1）＝5时，有φ（b）＝2，φ（c）＝6或φ（b）＝6，φ（c）＝2；当（φ（b）－1）（φ（c）－1）＝7时，有φ（b）＝2，φ（c）＝8或φ（b）＝8，φ（c）＝2.这4种情况中都有φ（b）＝2或φ（c）＝2，结合φ（a）＝6，只需讨论φ（a）＝6，φ（b）＝2.此时，有a＝7，9，14，18；b＝3，4，6.从而，方程（1）有正整数解（a，b，c）＝（9，3，5），（18，3，5），（9，5，3），（18，5，3），（9，3，8），（9，8，3），（9，3，10），（9，10，3），（7，3，12），（7，12，3），（9，5，6），（9，6，5），（7，3，7），（7，3，14），（7，7，3），（7，14，3），（7，7，4），（7，4，7），（7，7，6），（7，6，7），（14，3，7），（14，7，3），（7，3，20），（7，3，16），（7，20，3），（7，16，3），（7，4，15），（7，15，4）.

对上述正整数解进行归纳即可得本文结论.证毕.

［1］ 瞿云云，曹慧，牟全武.关于广义Ramanujan-Nagell方程x2－D＝3n的解数［J］.东北师大学报：自然科学版，2014，46（4）：52-55.

［2］ 吕志宏.两个数论函数及其方程［J］.纯粹数学与应用数学，2006，22（3）：303-306.

［3］ 吕志宏.一个包含Euler函数的方程［J］.西北大学学报：自然科学版，2006，36（1）：17-20.

［4］ 田呈亮，付静，白维祖.一个包含欧拉函数的方程［J］.纯粹数学与应用数学，2010，26（1）：96-98.

［5］ 左可正.含欧拉函数不定方程的可解性探讨［J］.黄石理工学院学报，2008，24（2）：49-50.

［6］ 陈斌，吉宇锋.关于一类包含Euler函数方程的解［J］.河南科学，2009，27（12）：1500-1501.

［7］ 刘艳艳.一个算术函数方程及其正整数解［J］.西安石油大学学报：自然科学版，2012，27（2）：108-110.

［8］ 呼家源，秦伟.一个包含Smarandache Ceil函数的对偶函数及Euler函数的方程及其可解性［J］.西北大学学报：自然科学版，2013，43（3）：364-366.

［9］ 孙翠芳，程智.关于方程φ（xyz）＝2（φ（x）＋φ（y）＋φ（z））［J］.数学的实践与认识，2012，42（23）：267-271.

［10］ ROSEN K H.Elementary theory and its applications［M］.Fifth edition.NJ：Pearson Educatin，Inc，Addison Wesley，2005：225.

［11］ 姜友谊.关于Euler函数方程φ（x）＝m的解［J］.重庆工业管理学院学报，1998，12（5）：91-94.

The positive integer solutions of an equation on the Euler function

ZHANG Si-bao1，LIU Qi-kuan2
（1.School of Mathematics and Statistics，Kashgar University，Kashgar 844008，China；2.Department of Mathematics，Kunming University，Kunming 650214，China）

The main purpose of this paper is to study the solvability of the equationφ（abc）＝6（φ（a）＋φ（b）＋φ（c）），and all positive integer solutions were obtained by using the elementary method，where φ（n）is Euler function.

Euler function；diophantine equation；positive integer solutions

O 156 ［学科代码］ 110·17

A

（责任编辑：陶 理）

1000-1832（2015）03-0049-06

10.16163／j.cnki.22-1123／n.2015.03.011

2013-10-16

四川省应用基础研究计划项目（2010JY0079）；昆明学院引进人才科研项目（YJL12005）.

张四保（1978—），男，硕士，副教授，主要从事数论研究.