抛物系统的最优初值控制问题

赵 坚，高 夯

（1.国家开放大学教育学部，北京100039；2.东北师范大学数学与统计学院，吉林长春130024）

抛物系统的最优初值控制问题

赵 坚1，高 夯2

（1.国家开放大学教育学部，北京100039；2.东北师范大学数学与统计学院，吉林长春130024）

讨论了抛物型方程支配系统初值的最优控制问题，得到了新形式最优控制的必要条件，其结果丰富了分布参数系统的控制理论.

抛物系统；最优控制；必要条件

1 问题的提出

本文讨论如下的问题：

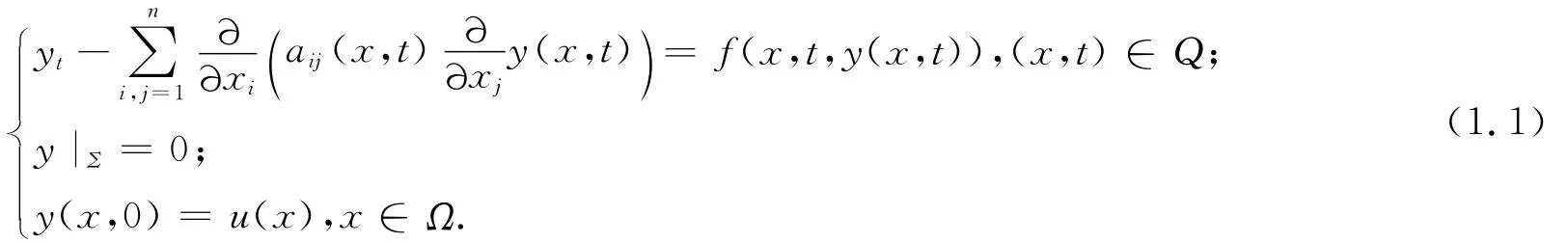
其中，Q＝Ω×（0，T），Ω⊂Rn是一个具有光滑边界的有界区域，

是控制函数，U是一个有界闭集.在一些工程问题中，只有初始状态是人们可以控制的.例如，非智能的弹道控制（人们只能控制初始的发射速度与发射角度），电子对抗中的初始信号等.在前人的工作中，人们只讨论了分布控制的情形，即

的情形［1－5］，初值u（x）是给定的函数，而在本文中初值是控制变量.

我们假设：

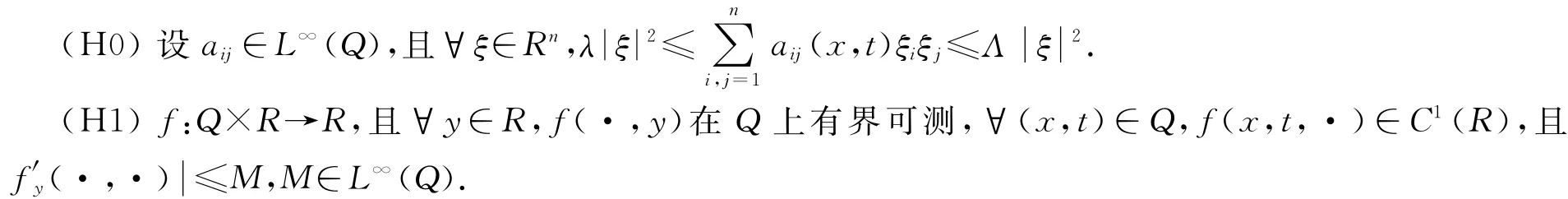
由文献［6］知，系统（1.1）存在唯一解，故对于u∈L∞（Ω，U）可定义

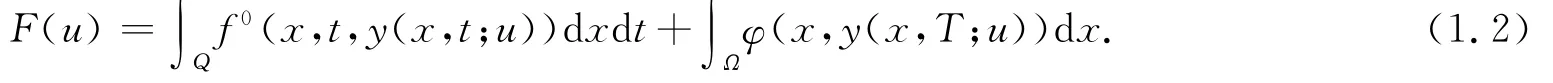
其中f0与φ满足如下的条件：

（H2）f0：Q×R→R，且∀y∈R，f0（·，y）可积，∀（x，t）∈Q，f0（x，t，·）∈C1（R）.

（H3）φ：Ω×R→R，且∀y∈R，φ（·，y）可积，∀x∈Ω，φ（x，·）∈C1（R）.

若存在¯u∈L∞（Ω，U），使得

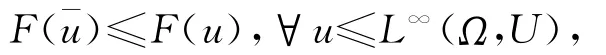
则称¯u是最优初值，称¯y（x，t）＝y（x，t，¯u）是最优状态，称（¯y，¯u）是最优对.

定理 设条件（H0）—（H3）被满足，且（¯y，¯u）是最优对，则有如下的最大值原理成立：

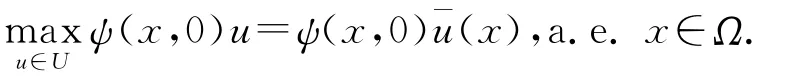
的解.

2 定理的证明

在本文问题的讨论中，主要使用的工具是针状变分与Liapounoff定理.首先给出如下的引理：

引理1（Liapounoff定理） 设y∈L′（Ω，Rn），λ∈（0，1）是一个常数，则存在可测集E∈Ω，使得m（E）＝λm（Ω），且

该引理的证明见文献［2］.

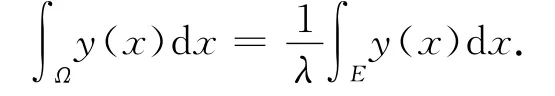
其次分如下的步骤来完成本文定理的证明：

第一步，对系统（1.1）做变分.为此，先对控制变量做扰动.

∀u∈L∞（Ω，U），∀ε＞0，选取Ωε⊂Ω，measΩε＝εmeasΩ.

令

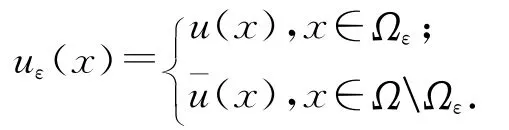
记yε（x，t）＝y（x，t；uε），有如下的引理：

引理2 存在常数k，使得‖yε－y‖W12，1（Q）≤kε.

证明 因yε与y 满足初值为uε与u的系统（1.1），故有

其中ζ＝¯y＋θ（yε－¯y）.由文献［6］即可知该引理成立.

引理3 在条件（H0）－（H3）下，有

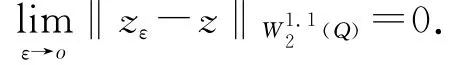
证明 由系统（2.1）与（2.2）可得

由系统（2.2）可知，存在常数k，使得｜z（x，t）｜≤k，且

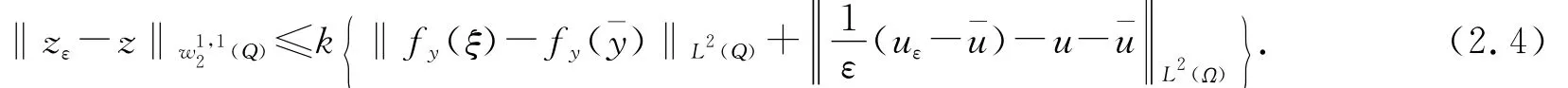
显然有

而对于（2.4）式右端的第二项，有

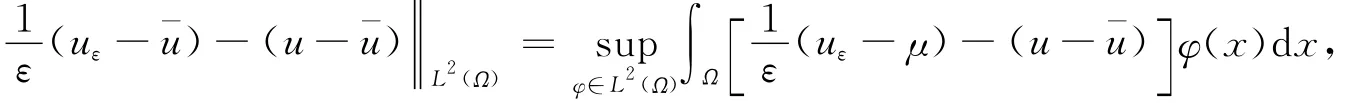
故∀δ＞0，存在φ0∈L2（Ω），使得

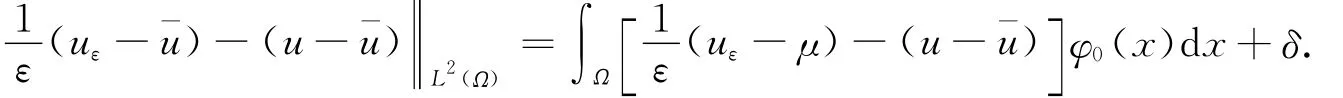
由引理1可知，对于函数［u（x）－¯u（x）］φ0（x），存在Ωε⊂Ω，m（Ωε）＝εm（Ω），使得

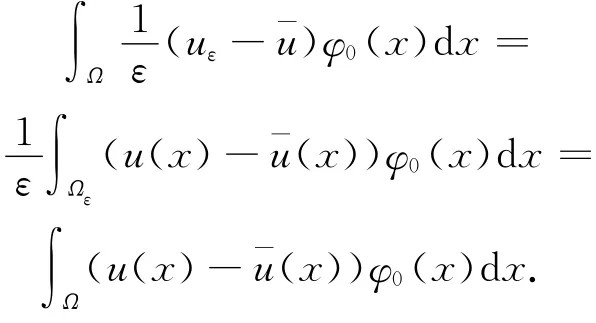
即

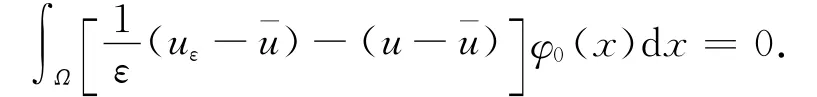
由δ的任意性，故有

我们引入方程

称方程（2.5）是方程（2.2）的对偶方程，方程（2.5）在W1，12（Q）中存在唯一解.

第二步，对泛函（1.2）做变分.显然有

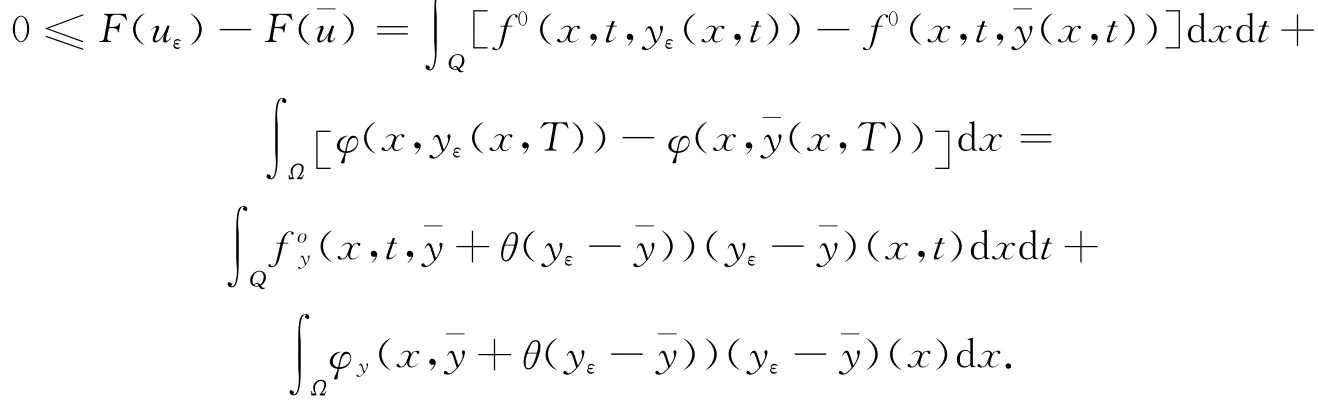
上式两端同除ε，并取极限，得

∀x0∈Ω做球B（x0，δ）⊂Ω，且取

则上式成为

将上式同除measB（xo，δ），且令δ→0，根据ψ（x，0）¯u（x）的Lebesgue点稠密，进而有

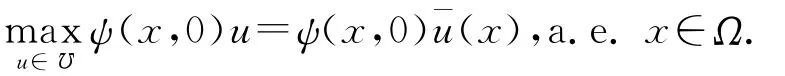
综上所述，定理得证.

［1］ BARBU V.Analysis and control of nonlinear infinite dimensional systems［M］.New York：Academic Press，1933：258-305.

［2］ LI X，YONG J.Optimal control theory for infinite dimensional systems［M］.Birkhauser Boston：Cambrige MA，1995：168-179.

［3］ WANG G，WANG L.Maximum principle of optimal control of non-well posed differential equations［J］.Nonlinear Anal，2003，52：41-67.

［4］ GAO H.Optimality condition for a class of semilinear parabolic equations［J］.Acta Math Sinica，1999，42（4）：705-714.

［5］ LIN P，WANG G.Some properties for blow-up parabolic equation［J］.J Math Pure Appl，2014，101：223-255.

［6］ EVANS L.Parabolic differential equations［M］.Rhode Island：American Mathematical Society，1998：502-518.

Optimal initial value control problem for parabolic equation systems

ZHAO Jian1，GAO Hang2
（1.School of Education，Open University of China，Beijing 100039，China；2.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China）

In this paper，We discuss the optimal initial value control problem for parabolic differential equation systems.We obtain the necessary conditions for optimal initial value control by a new maximum principle.The results given in this paper may enrich the control theory for infinite dimension control systems.

parabolic equation system；optimal control；necessary conditions

O 232 ［学科代码］ 120·30

A

（责任编辑：陶 理）

1000-1832（2015）03-0001-04

10.16163／j.cnki.22-1123／n.2015.03.001

2015-03-26

国家自然科学基金资助项目（11171060）；国家重点基础研究发展计划（973计划）项目（2011CB8080002）.

赵坚（1958—），女，教授，主要从事控制数学理论研究；通讯作者：高夯（1956—），男，博士，教授，博士研究生导师，主要从事控制数学理论研究.