离散时间T-S模糊系统的新型状态反馈控制设计
赵成龙,薛 欣,张 友
(1.泰山职业技术学院,山东泰安271000;2.泰山学院数学与统计学院,山东泰安271021;3.东北师范大学计算机科学与信息技术学院,吉林长春130117)
离散时间T-S模糊系统的新型状态反馈控制设计
赵成龙1,薛 欣2,张 友3
(1.泰山职业技术学院,山东泰安271000;2.泰山学院数学与统计学院,山东泰安271021;3.东北师范大学计算机科学与信息技术学院,吉林长春130117)
针对离散时间T-S模糊系统的控制设计问题,设计了一种新型的非-PDC型模糊状态反馈控制器.在模糊状态反馈控制器设计过程中,采用了一种全新的模糊李亚普诺夫函数和一种新颖的松弛变量技术,可以为状态反馈控制设计引入更多的自由度,因此可以获得比以往结果保守性更小的模糊镇定控制条件.特别是以线性矩阵不等式形式给出的模糊镇定控制条件可以很方便地利用Matlab工具箱来进行求解.最后,使用一个经典的仿真算例验证了所得结果的有效性.
离散时间系统;状态反馈;T-S模糊模型;松弛变量技术;线性矩阵不等式
0 引言
在实际工业过程控制中,相当数量的控制对象属于非线性系统,因而对于非线性控制系统所开展的稳定性分析和控制设计方向的研究吸引了众多控制领域学者的注意力和研究兴趣.自从20世纪80年代中期以来,T-S模糊模型[1]已被广泛作为有效处理非线性控制系统的稳定性分析和控制设计等问题的手段.特别是王立新在文献[2]中成功证明了T-S模糊模型能够以任意精度逼近定义在紧集上的一个连续非线性函数,从理论上保证了T-S模糊模型处理非线性控制系统问题可行性.在使用T-S模糊模型的非线性系统控制设计研究中,文献[3]给出了著名的并联分布补偿(PDC)技术,构建了模糊状态反馈控制的一般化设计架构,引发了该研究方向的一股研究热潮[4-8].需要指出的是,基于上述PDC技术获得的模糊镇定控制条件的保守性通常比较大,在很大程度上限制了T-S模糊模型在非线性控制领域的正常使用.于是,很多文献在如何降低基于PDC技术的模糊控制系统镇定控制条件保守性方面做了大量同质化的研究工作[4-8].其中,文献[4]首次通过引入附加变量的思想把各个模糊子系统之间的耦合关系投射到一个增广矩阵内,得到相比文献[3]保守性要小的模糊镇定控制条件;文献[8]将数学领域的Polya's定理推广到模糊控制设计中,完成了基于PDC技术框架下的一种渐近充要条件的理论性证明.然而,受制于PDC技术本身固有的缺点,上述渐近充要条件在本质上依然具有较大的保守性,是因为所使用的是普通二次型李亚普诺夫函数,因而结果为常规二次型镇定控制条件[9].需要特别指出的是模糊隶属函数为T-S模糊系统的重要组成部分,因此在系统的状态反馈控制设计过程中,如何将蕴含在模糊隶属函数的有用信息融合和运用是结果保守性降低的一条有效途径[9-11].在使用模糊李亚普诺夫函数进行稳定性分析时,文献[12]设计了一种针对离散时间T-S模糊系统的非-PDC状态反馈控制律,显著减少了已有结果的保守性.
为了进一步减少离散时间T-S模糊系统控制设计的保守性,本文提出了一种新型的非-PDC模糊状态反馈控制器.证明已有文献中的模糊状态反馈控制器为本文提出非-PDC模糊状态反馈控制器的一个特例.此外,本文还设计了一种新型的模糊李亚普诺夫函数和一种与之配套的松弛变量技术来进一步减小相关结果的保守性.上述方法的协同实施使得在模糊控制设计时可以更有效地考虑到蕴含在模糊隶属函数中的可用系统信息,得到比已有文献结果的保守性更小的控制设计条件,最终达到扩大T-S模糊模型在非线性控制领域的应用范围的目的.
1 预备知识
1.1 离散时间T-S模糊系统
我们考虑一个由若干组模糊规则所组成的离散时间T-S模糊系统[1]:
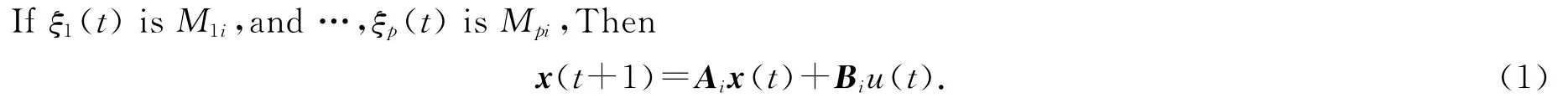
其中:x(t)∈Rn表示系统状态变量;u(t)∈Rm为系统控制输入信号;Ai∈Rn×n;Bi∈Rn×m;ξ1(t),…,ξp(t)为模糊系统前件变量;r表示模糊规则数;Mij(i=1,2,…,p;j=1,2,…,r)为模糊集函数.
上述离散时间模糊系统的全局模型可以表示为
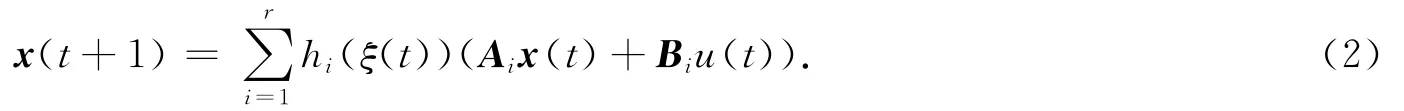
1.2 放松性离散时间T-S模糊状态反馈控制器
基于非-PDC控制思想,文献[12]提出了一种模糊状态反馈控制器
基于上述模糊状态反馈控制器,文献[12]给出了一组不同于以往的离散时间T-S模糊控制系统镇定控制条件,它与先前文献相比具有更弱的保守性特征.在其证明中,如下数学引理起到了一定作用.
引理1[12]对于适当维数的矩阵A,P+和P,矩阵不等式ATP+A-P<0成立的一个充分条件为存在矩阵并使得如下矩阵不等式成立:

其中He(G)=G+GT.
注1 文献[12]在系统设计中考虑了不同于传统PDC技术的状态反馈控制器,仿真实验证明它所得镇定控制的保守性比文献的小.另一方面,状态反馈控制器(3)和模糊李亚普诺夫函数的共同作用则为保守性的持续减弱发挥了作用.这也给我们以启示:若设计者从控制器组成结构、模糊李亚普诺夫函数组成架构、松弛变量引入方法等不同方面进行协调优化,充分地将蕴含在模糊隶属函数的有用信息融合控制设计中,则可以为获得保守性更弱的离散时间T-S模糊系统镇定控制条件提供保证.
2 主要结果
文献[12]中所得到的模糊镇定控制条件的保守性还是比较大的,这也在很大程度上限制文献[12]所得理论研究成果在实际控制设计中的广泛使用.为达到进一步减弱模糊镇定控制条件保守性的目的,我们提出一种新型的非-PDC状态反馈控制器设计方法以及与之配套的模糊李亚普诺夫函数,辅之相应的松弛变量技术,保证在系统控制设计中能够更加有效地考虑蕴含在隶属函数中的有用信息,最大限度地减弱所得结果的保守性,以期增大T-S模糊模型在实际控制系统设计应用中的范围.
首先,给出如下形式的一种新型非-PDC模糊状态反馈控制器.即
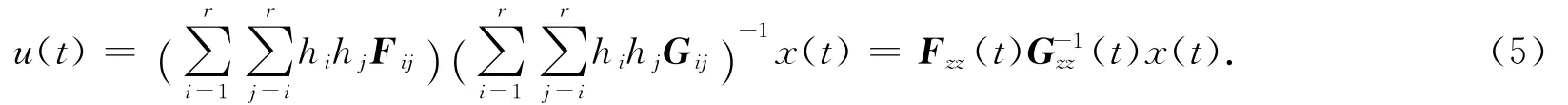
其中矩阵Fij和Gij表示待求解的控制增益矩阵.把新型非-PDC模糊状态反馈控制器(5)代入到离散时间T-S模糊控制系统(2)之后,相应离散时间T-S模糊控制系统(2)的闭环表示形式变为

这里
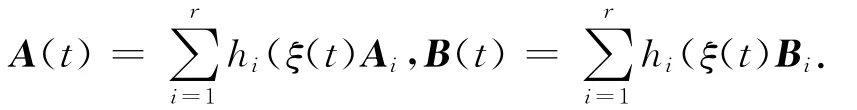
定理1 在新型非-PDC模糊状态反馈控制器(5)作用下的离散时间T-S模糊控制系统(2),若有矩阵
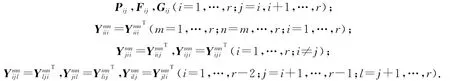
使得如下线性矩阵不等式成立:


其中:则离散时间T-S模糊闭环控制系统(6)是渐近稳定的.
证明 这里,我们用x,hi来代替x(t),hi(ξ(t)).并且使用如下形式的模糊李亚普诺夫函数

其中:
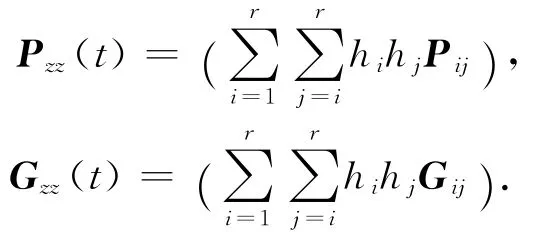
对V(x)沿闭环系统(6)求取一阶差分可得
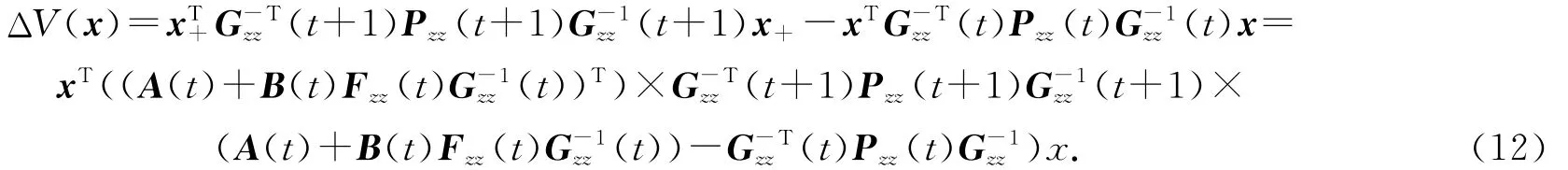
由(12)式可以看出,如果如下不等式成立则系统(6)是渐近稳定的:
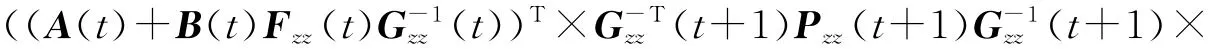
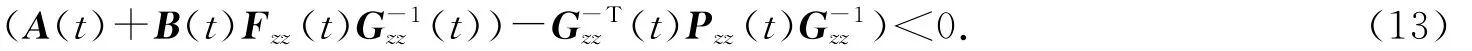
对(13)式两边左乘和右乘Gzz(t)后得到
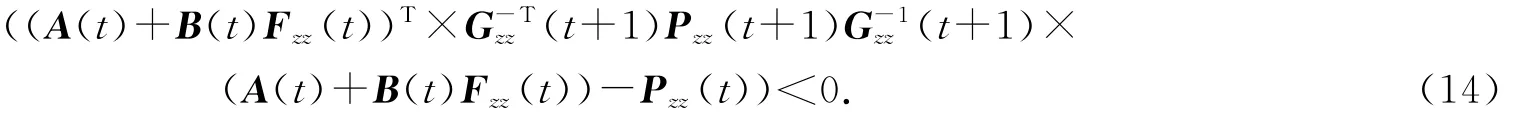
使用引理1,可得保证不等式(14)成立的一个充分条件为如下不等式成立:

对式Π变换求和次序可得
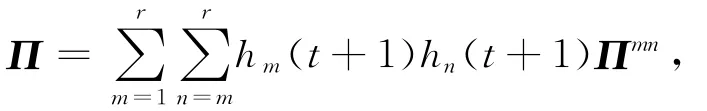
式中

进一步,有
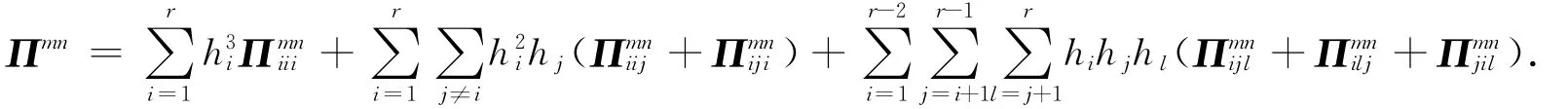
此时,由(7)—(9)式可得
其中:
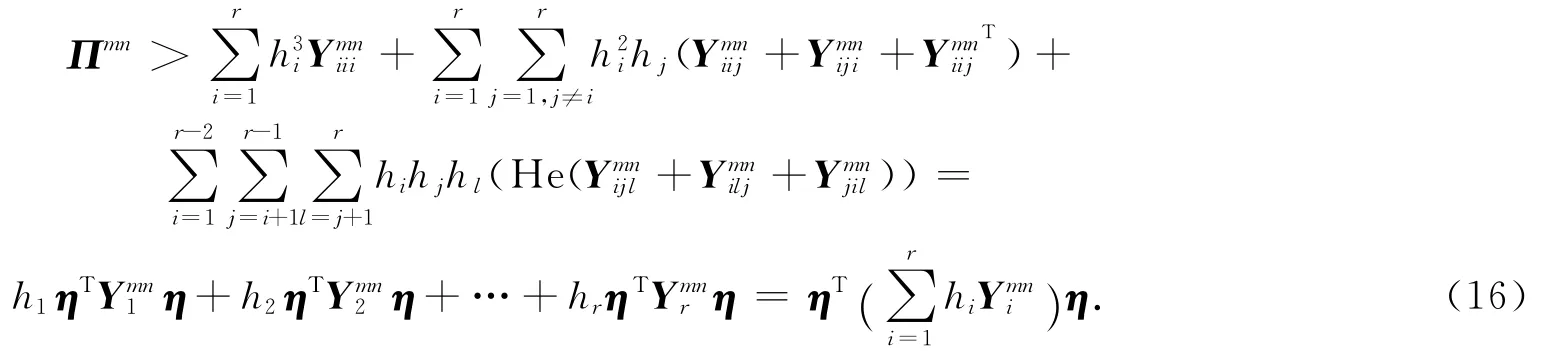

于是,若(10)式成立,那么Πmn>0也成立.换句话说,离散时间T-S模糊闭环控制系统(6)是渐近稳定的,定理得证.
注2 通过设计新型的非-PDC模糊状态反馈控制器(5)、模糊李亚普诺夫函数(13)以及定理中的松弛变量引入方法等措施,所得到的T-S模型系统镇定控制条件(7)—(10)具有比以往结果更小的保守性.需要指出的是,如果令Fij=Fi+Fj和Gij=Gi+Gj,则本文给出的新型模糊状态控制器(5)退化为文献[12]中提出的模糊状态控制器(3),也就是说,文献[12]中所提出的控制器是本文方法的一个特例.
3 仿真验证
考虑下面一类离散时间T-S模糊控制系统[12]
其中
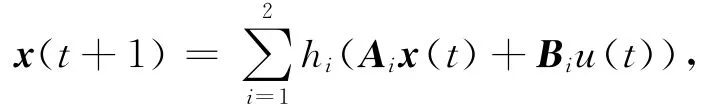


这里,使用可调参数β的可镇定范围来进行定理1与文献[12]方法之间保守性强弱关系的比较.
不失一般性,采用文献[12]给出的已有方法进行控制设计时,可调参数β的镇定范围为β≤1.69;而采用本文给出的定理1进行控制设计时可调参数β的可镇定范围为β≤1.76.因此,从以上对比结果中可以知道定理1对应的可行域要大于文献[12]方法对应的可行域,换句话说,定理一得到的模糊镇定控制条件对应的保守性更弱.
设定β=1.76,该点采用文献[12]给出的已有方法进行控制设计时是不可行点,但在采用本文给出的定理1进行控制设计时具有可行解,即上述2种设计方法中唯有使用定理1才能使得该系统渐近稳定.对定理1给出的相关线性矩阵不等式(7)—(10)进行求解,得到新型非-PDC模糊控制律(5)的系统控制增益矩阵如下:

设定系统初始值为x(0)=[1.76,2.49]T,在图1中给出了在上述控制增益矩阵控制作用下系统的状态轨迹变化情况.由图1可以看出在控制器控制下整个闭环系统是渐近稳定的.

图1 闭环系统状态轨迹图
4 结语
本文给出了一种离散时间T-S模糊控制系统的新型状态反馈控制设计结果.提出新型的非-PDC状态反馈控制器、更丰富内涵的模糊李亚普诺夫函数和与之配套的松弛变量技术,能够显著降低模糊状态反馈控制设计结果的保守性.从仿真结果可以看出本文所给出方法是有效的.
[1] TAKAGI T,SUGENO M.Fuzzy identification of systems and its application to modeling and control[J].IEEE Transactions on Syst Man Cybern,1985,15:116-132.
[2] FENG G,CAO S,REES W.An approach to H∞control of a class of nonlinear systems[J].Automatica,1996,32(10):1469-1474.
[3] WANGH,TANAKA K,GRIFFIN M.An approach to fuzzy control of nonlinear systems:stability and design issues[J].IEEE Transactions on Fuzzy Systems,1996,4(1):14-23.
[4] TANAKA K,IKEDA T,WANG H.Fuzzy regulators and fuzzy observers:Relaxed conditions and LMI-based designs[J].IEEE Transactions on Fuzzy Systems,1998,6(2):250-265.
[5] KIM E,LEE H.New approaches to relaxed quadratic stability conditions of fuzzy systems[J].IEEE Transactions on Fuzzy Systems,2000,8(5):523-534.
[6] LIU X,ZHANG Q.New approaches to H∞controller designs based on fuzzy observers for T-S fuzzy systems via LMI[J].Automatica,2003,39(9):1571-1582.
[7] DONG J X,YANG G H.State feedback control of continuous-time T-S fuzzy systems via switched fuzzy controller[J].Information Sciences,2008,178(6):1680-1695.
[8] SALA A,ARINO C.Asymptotically necessary and sufficient conditions for stability and performance in fuzzy control[J].Fuzzy Sets and Syetms,2007,158(24):2671-2686.
[9] SALA A,ARINO C.Relaxed stability and performance conditions for T-S fuzzy systems with knowledge on membership function overlap[J].IEEE Transactions on Syst Man Cybern,2007,37(3):727-732.
[10] MOZELI L A,PALHARES R M,SOUZA F O,et al.Reducing conservativeness in recent stability conditions of T-S fuzzy systems[J].Automatica,2009,45(6):1580-1583.
[11] ZHANG H,XIE X.Relaxed stability conditions for continuous-time T-S fuzzy control systems via augmented multi-indexed matrix approach[J].IEEE Transactions on Fuzzy Systems,2011,19(3):478-492.
[12] GUERRA T M,VERMRIREN L.LMI-based relaxed nonquadratic stabilization conditions for nonlinear systems in the Takagi-SUGENO'S form[J].Automatica,2004,40(5):823-829.
Novel state feedback control design of discrete-time T-S fuzzy systems
ZHAO Cheng-long1,XUE Xin2,ZHANG You3
(1.Taishan Ploytechnical Institute,Taian 271000,China;2.College of Mathematics and Statistics,Taishan University,Taian 271021,China;3.School of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China)
A new kind of non-PDC fuzzy state feedback controller has been proposed for dealing with the problem of control synthesis of the discrete-time Takagi-Sugeno fuzzy systems.Both a new fuzzy Lyapunov function and a novel slack variable technique have been developed in the process of fuzzy state feedback control designs.Since more freedom is introduced in virtue of the above measures,the obtained stabilization conditions are less conservative than existing ones.In particular,the underlying fuzzy stabilization conditions proposed in this paper are in terms of linear matrix inequality which is easy to be solved by using the Matlab tools.Finally,a classical numerical example is also provided to illustrate the effectiveness of the proposed results.
discrete-time systems;state feedback;T-S fuzzy model;slack variable technique;linear matrix inequality(LMI)
TP 273 [学科代码] 520·30
A
(责任编辑:石绍庆)
1000-1832(2015)03-0072-06
10.16163/j.cnki.22-1123/n.2015.03.016
2014-07-04
国家自然科学基金资助项目(21127010).
赵成龙(1969—),男,副教授,主要从事计算机应用及数据挖掘;通讯作者:张友(1971—),男,副教授,主要从事控制论与模式识别研究.

