一类分数阶脉冲微分方程边值问题的多重正解
张爱华,胡卫敏
(1.伊犁师范学院数学与统计学院,新疆伊宁835000;2.菏泽市第二中学,山东菏泽274000)
一类分数阶脉冲微分方程边值问题的多重正解
张爱华1,2,胡卫敏1
(1.伊犁师范学院数学与统计学院,新疆伊宁835000;2.菏泽市第二中学,山东菏泽274000)
通过锥拉伸与锥压缩不动点定理得到了一类非线性分数阶脉冲微分方程边值问题正解的存在性和多重性结果.
脉冲微分方程;边值问题;分数阶导数;锥拉伸与锥压缩不动点定理
0 引言
非线性脉冲微分方程是描述状态在某些时刻发生瞬间突变的过程,因其能更深刻、精确地反映事物的变化规律,日益引起人们的重视,使它在物理、经济、生命科学、医学、航天技术、工程技术、人口动态分布等领域都有广泛的应用[1-2].随着脉冲微分方程理论的发展,人们开始关注脉冲微分方程边值问题的研究.关于整数阶脉冲微分方程两点、三点和多点边值问题解的存在性和唯一性的研究已经取得了一定的成果[3-5],但是很少有文献研究非线性分数阶脉冲微分方程边值问题解的存在性[6-12].
本文运用锥拉伸与锥压缩不动点定理给出如下分数阶脉冲边值问题:

正解的存在性和多重性.其中:2<α≤3;CDα0+是Caputo分数阶导数;R+=[0,∞);f∈C([0,1]×R+× R+×R+,R+);xk,yk,zk∈C(R+,R+);J=[0,1],J′=J\{t1,t2,…,tm},k=1,2,…,m;J0=[0,t1],Jk=(tk,tk+1],0=t0<t1<…<tm<tm+1=1;Δu(tk)=u(t+k)-u(t-k),u(t+k)与u(t-k)分别表示u(t)在tk处的右极限与左极限,且u(t-k)=u(tk),Δu′(tk)和Δu″(tk)对u′(t)和u″(t)也有类似定义.此外

K∈C(D,R+),D={(t,s)∈J×J|t≥s},H∈C(J×J,R+).
定义PC(J,R)={u:J→R|u∈C(Jk),k=0,1,2,…,m;u(t+k)存在,k=1,2,…,m},则PC(J,R)是以为范数的Banach空间.
若u∈PC2(J,R)∩AC3(J′,R)满足(1),并且u(t)>0,t∈J,则称u为问题(1)的正解.
1 预备知识
首先,我们给出一些分数阶微积分理论的定义和定理,参见文献[12-16].定义1.1[13]函数f:[0,∞)→R的α>0阶Riemann-Liouville积分是指

其中右边是在[0,∞)上逐点定义的.
定义1.2[14]函数f:[0,∞)→R的α>0阶Riemann-Liouville微分是指

其中n=[α]+1,右边是在[0,∞)上逐点定义的.特别地,当α=n时,Dn0+f(t)=f(n)(t).
定义1.3[15]函数f:[0,∞)→R的α>0阶Caputo微分是指
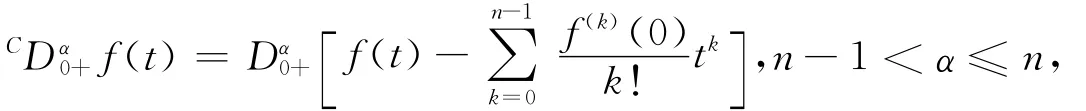
其中右边是在[0,∞)上逐点定义的.特别地,当α=n时,CDn0+f(t)=f(n)(t).
引理1.1[15]设n-1<α≤n,f(t)∈Cn([0,∞),R),则:
引理1.2[12]令0<α<1,h∈C([0,T],R),函数x∈C([0,T],R)是分数阶边值问题

的解当且仅当x是如下积分方程的解:
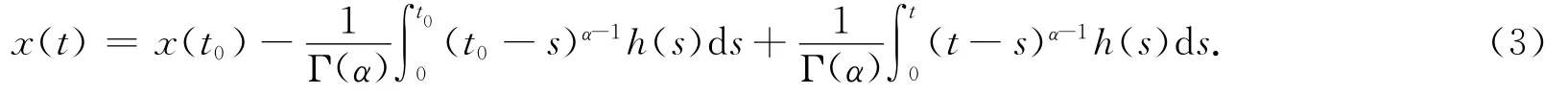
引理1.3[16]令X是一个Banach空间,P⊂X是X中的一个锥.假设Ω1,Ω2⊂P为非空相对开集,且0∈Ω1⊂¯Ω1⊂Ω2,设T:P→P为全连续算子,满足下列条件之一:
(ⅰ)‖Tx‖≤‖x‖,x∈P∩∂Ω1,且‖Tx‖≥‖x‖,x∈P∩∂Ω2;
(ⅱ)‖Tx‖≥‖x‖,x∈P∩∂Ω1,且‖Tx‖≤‖x‖,x∈P∩∂Ω2.
则T在P∩(¯Ω2\Ω1)中有不动点.
引理1.4 令2<α≤3,假设h:[0,1]→R+是一个连续函数,则边值问题
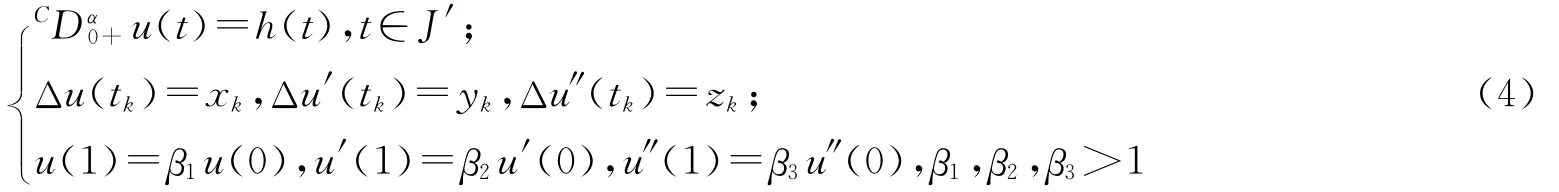
等价于积分方程
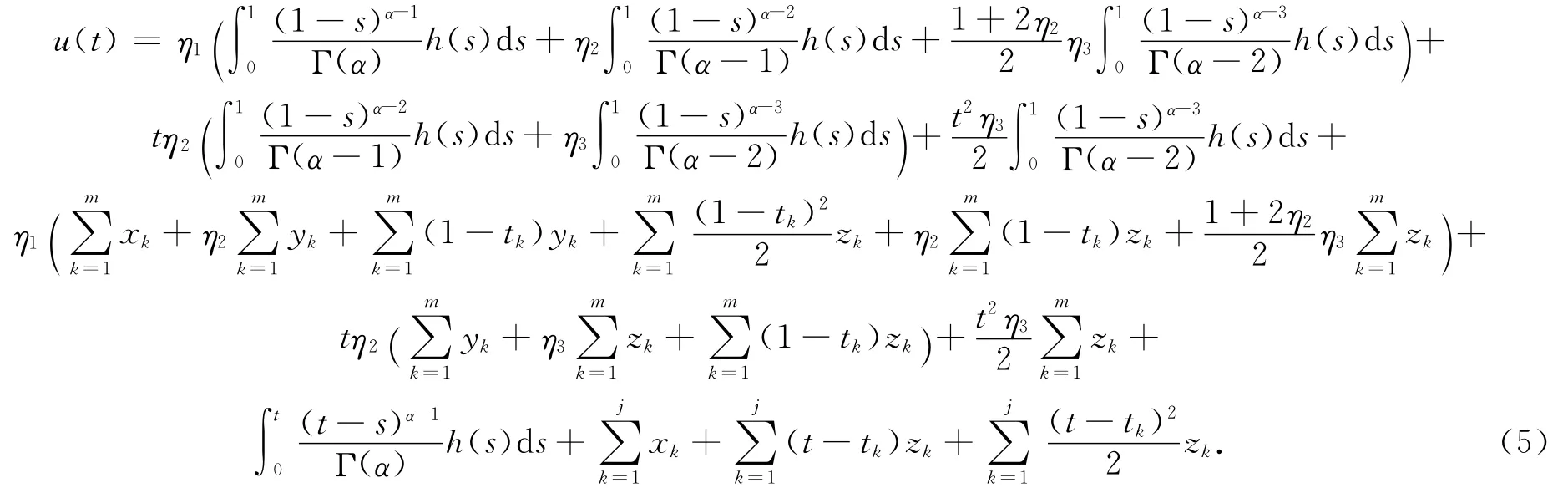
证明 令u(t)是问题(4)的解,利用引理1.1的(1),当t∈[0,t1]时,有
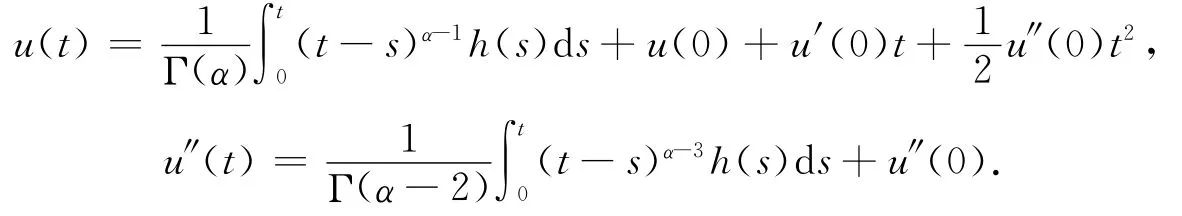
当t∈(t1,t2]时,由引理1.2及注1.1可得
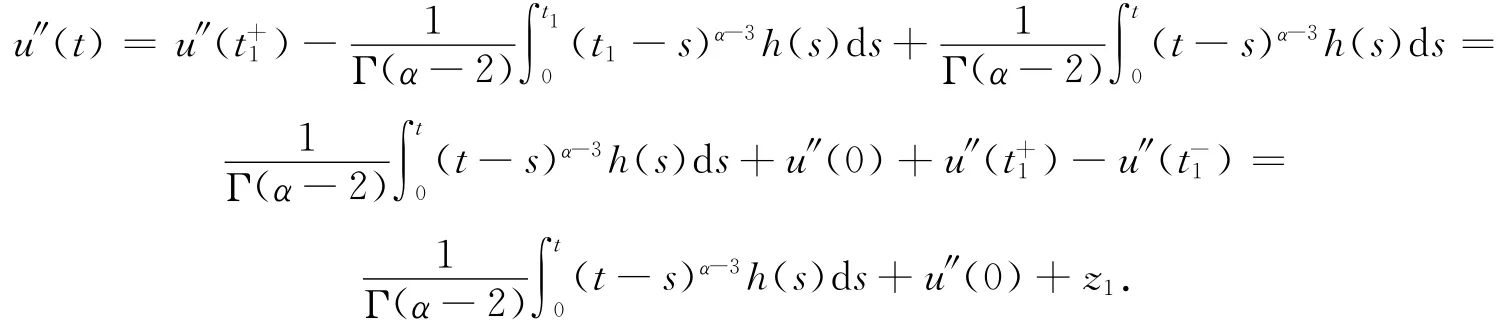
同理,当t∈(tj,tj+1]时,有
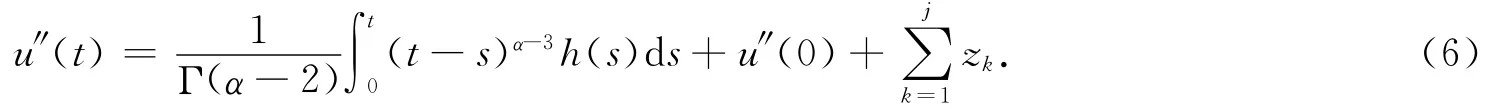
对(6)式从0到t进行2次积分,得

则

代入边界条件u(1)=β1u(0),u′(1)=β2u′(0),u″(1)=β3u″(0),有
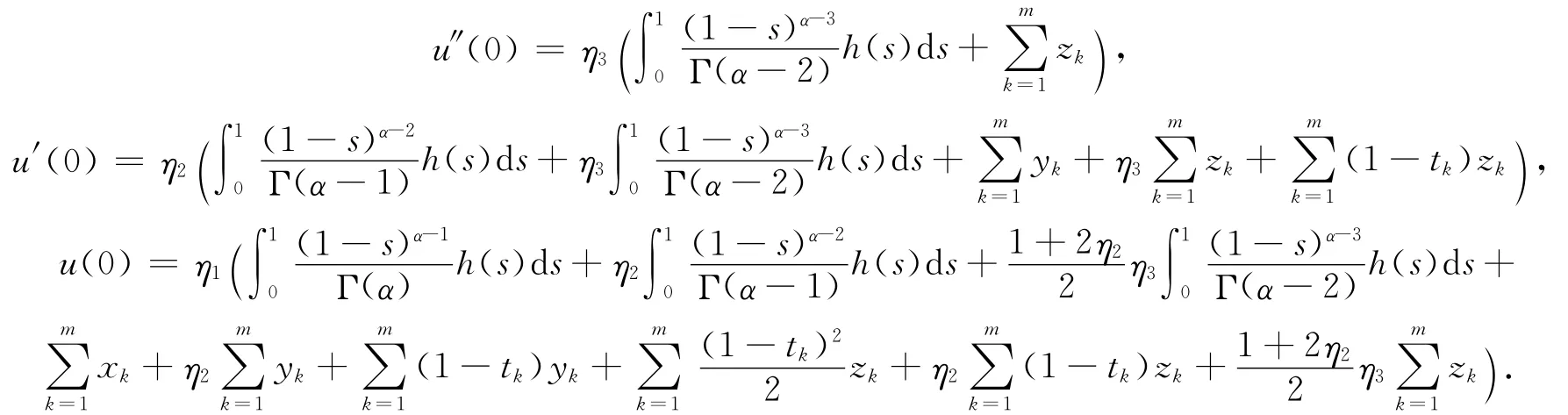
代入(7)式,得(5)式成立.
相反,若u(t)是方程(5)的解,由引理1.1的(2)和Caputo导数的定义可得u(t)是(4)式的解,证毕.
记σ(t)∶=f(t,u(t),(Tu)(t),(Su)(t)),由引理1.4可知边值问题(1)有解,等价于如下定义的积分算子F:PC(J,R)→PC(J,R)有不动点.
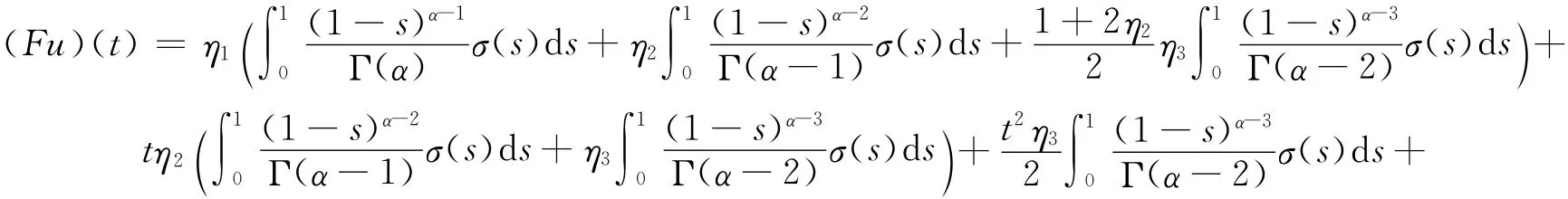
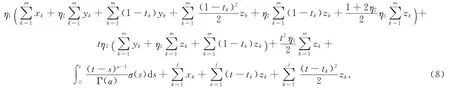
2 主要结论
为证明正解的存在性,现作如下假设:
(H1)存在常数k*,h*>0,使得

(H2)当u→∞时对t∈J一致成立.
(H3)当u→0+时对t∈J一致成立.
(H4)当u→0+时0,k=1,2,…,m.
(H5)对任意t∈J,存在非负连续函数a(t),ɡ(u,v,w),使得
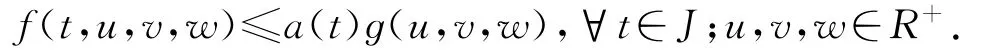
引理2.1 若条件(H1)成立,则F:Q→Q是全连续的.
证明 首先,由函数f,xk,yk,zk的连续性以及Lebesgue控制收敛定理,易知算子F也是连续的.往证F:Q→Q.事实上,对任意u∈Q,存在r1≥‖u‖,
记
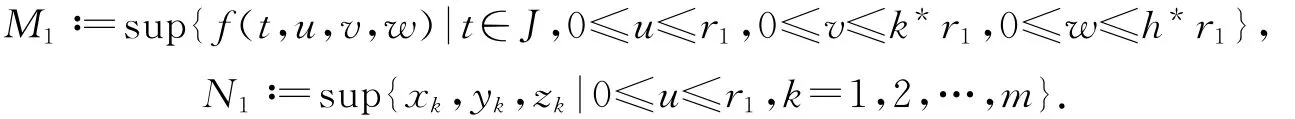
则
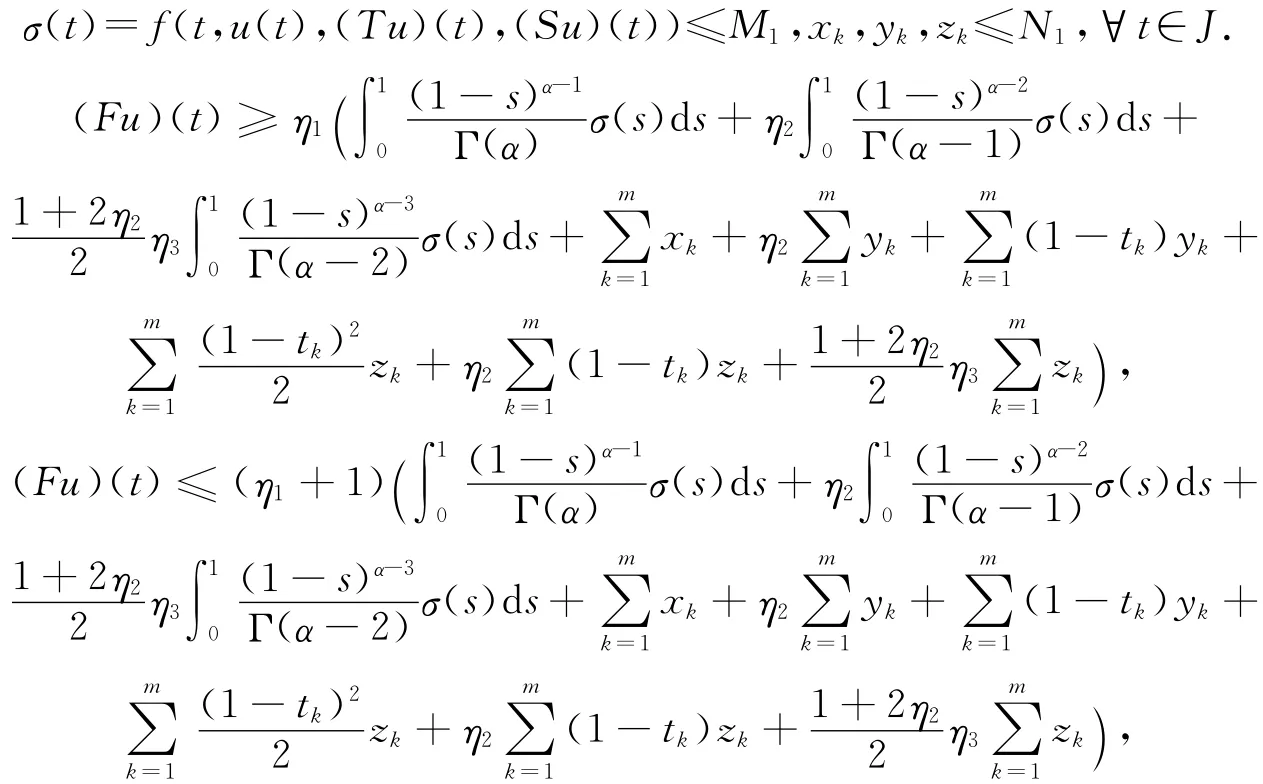
则
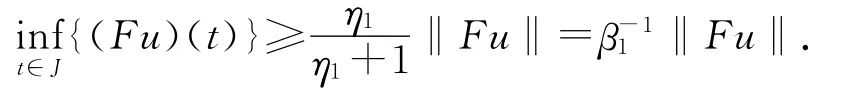
故Fu∈Q.从而F:Q→Q.
再证F映有界集为有界集.只需证明对任意u∈Q,存在常数l>0,使得‖Fu‖≤l,由以上证明过程可知,取l=(η1+1)(aM1+bN1)即可.
最后证F映有界集为Q中等度连续集.对任意tk<t<t′≤tk+1;k=0,1,2,…,m;u∈Q.有

由于当t′→t时,上述不等式右端趋于0,故F在每个区间Jk上等度连续.由广义的Arzela-Ascoli定理可知F是全连续算子.
定理2.1 若条件(H1),(H2),(H3)成立,并且存在r>0,使得(η1+1)(aMr+bNr)<r,其中
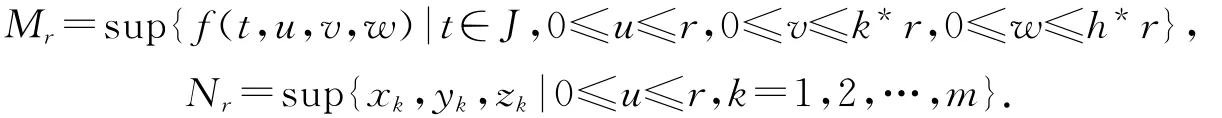
则边值问题(1)至少有两个正解u1和u2,满足

证明 由引理2.1知,(8)式所定义的算子F:Q→Q是全连续的.下面需要证明F在Q中有两个不动点u1和u2,满足0<‖u1‖<r<‖u2‖.由条件(H2)知,存在r1>0,使得
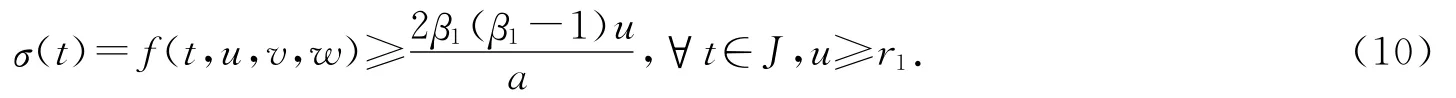
取r2>max{β1r1,r},对任意u∈Q,‖u‖=r2,有

由(10),(11)式及算子F的定义知
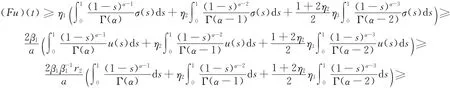
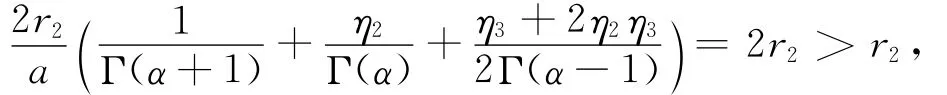
故
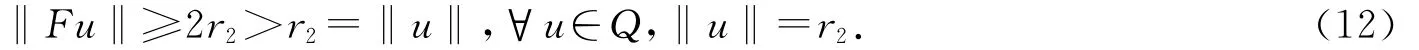
同理,由条件(H3)知,存在r3>0,使得
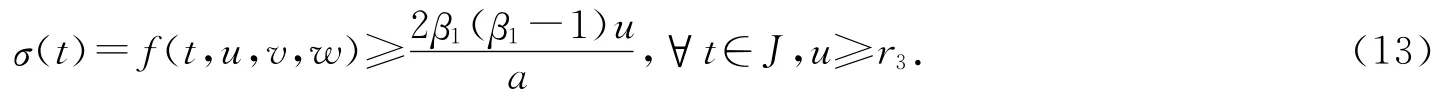
取0<r4<min{r3,r},对任意u∈Q,‖u‖=r4,有
则
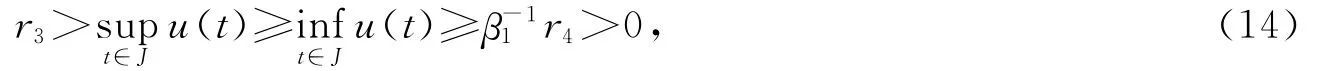

故
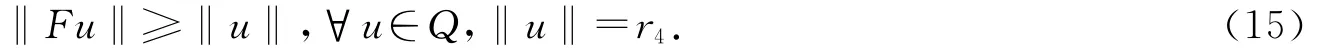
另一方面,对任意u∈Q,‖u‖=r,类似于(9)式有
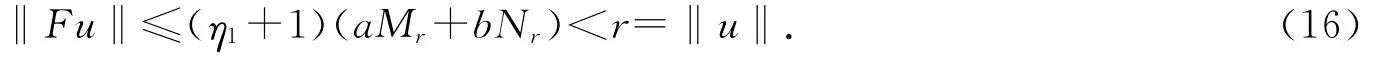
因为0<r4<r<r2,由(12),(15),(16)式及引理1.3得,F在Q中有两个不动点u1和u2,满足

定理2.2 若条件(H1),(H2),(H4),(H5)成立,并且当u+v+w→0+时,则边值问题(1)至少有一个正解u,满足
证明 如定理2.1的证明,取r2>β1r1>0,使得
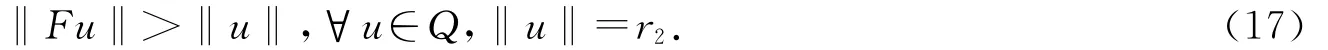
取ε0=[2(η1+1)(a(1+k*+h*)a*+b)]-1,由条件知,存在r5>0,使得
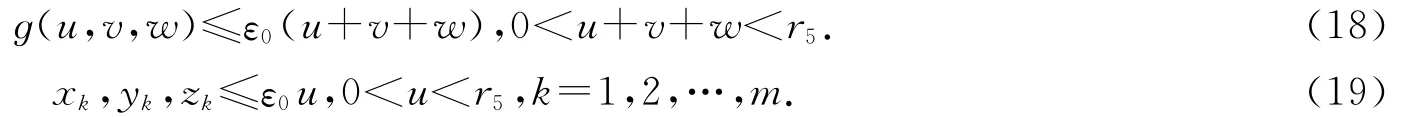
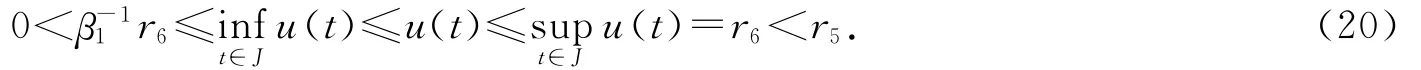
故

由条件(H5)可得
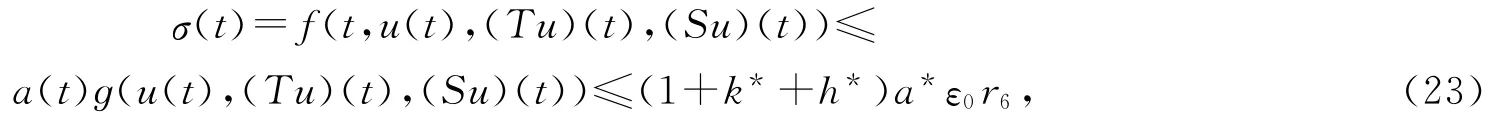
则
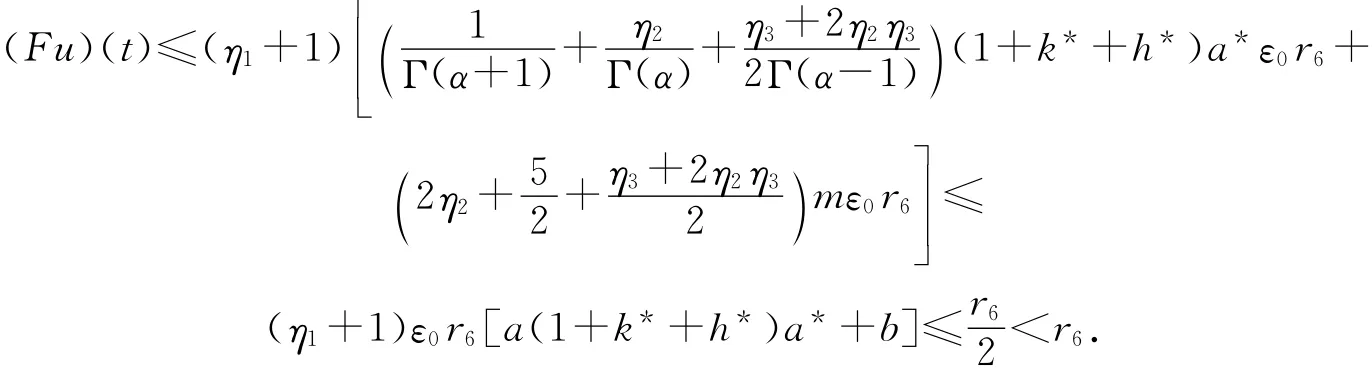
故
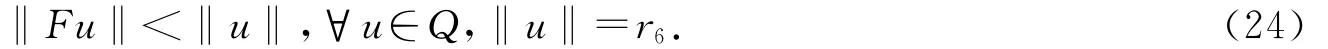
因0<r6<r2,由引理1.3得,算子F在Q中有不动点u,满足r6<‖u‖<r2.
[1] SAMKO S G,KILBAS A A,MARIˇCEV O I.Fractional integrals and derivatives[M].Yverdon:Gordon and Breach Science Publ,1993:366-398.
[2] PODLUBNY I.Fractional differential equations,mathematics in science and engineering[M].New York,London,Toronto:Academic Press,1999:243-313.
[3] DING WEI,WANG YU.New result for a class of impulsive differential equation with integral boundary conditions[J].Commun Nonlinear Sci Numer Simulat,2013,18(5):1095-1105.
[4] GUO DAJUN.Multiple positive solutions for first order impulsive singular integro-differential equations on the half line[J].Acta Mathematica Scientia,2012,32B(6):2176-2190.
[5] WANG XIAOHUAN,ZHANG JIHUI.Impulsive anti-periodic boundary value problem of first-order integro-differential equations[J].Journal of Computational and Applied Mathematics,2010,234(12):3261-3267.
[6] LI XIAOPING,CHEN FULAI,LI XUEZHU.Generalized anti-periodic boundary value problems of impulsive fractional differential equations[J].Commun Nonlinear Sci Numer Simulat,2013,18(1):28-41.
[7] LIU ZHENHAI,LI XIUWEN.Existence and uniqueness of solutions for the nonlinear impulsive fractional differential equations[J].Commun Nonlinear Sci Numer Simulat,2013,18(6):1362-1373.
[8] GUO TIANLIANG,JIANG WEI.Impulsive problems for fractional differential equations with boundary value conditions[J].Computers and Mathematics with Applications,2012,64(10):3281-3291.
[9] AHMAD BASHIR,SIVASUNDARAM S.Existence of solutions for impulsive integral boundary value problems of fractional order[J].Nonlinear Analysis:Hybrid Systems,2010,4:134-141.
[10] WANG GUOTAO,AHMAD BASHIR,ZHANG LIHONG.Impulsive anti-periodic boundary value problem for nonlinear differential equations of fractional order[J].Nonlinear Analysis,2011,74(3):792-804.
[11] CAO JIANXIN,CHEN HAIBO.Impulsive fractional differential equations with nonlinear boundary conditions[J].Mathematical and Computer Modelling,2012,55(3):303-311.
[12] CHEN FULAI.Coincidence degree and fractional boundary value problems with impulses[J].Computers and Mathematics with Applications,2012,64(10):3444-3455.
[13] 许晓婕,胡卫敏.一个新的分数阶微分方程边值问题正解的存在性结果[J].系统科学与数学,2012,32(5):580-590.
[14] 钟文勇.分数阶微分方程多点边值问题的正解[J].吉首大学学报:自然科学版,2010,31(1):9-12.
[15] KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterda:Elsevier Science B V,2006:59-90.
[16] BAI ZHANBING,LÜHAISHEN.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311(2):495-505.
Multiple positive solutions for a class of boundary value problem of impulsive fractional differential equations
ZHANG Ai-hua1,2,HU Wei-min1
(1.School of Mathematics and Statistics,Yili Normal University,Yining 835000,China;2.The Second High Middle School of Heze City,Heze 274000,China)
In this paper,we investigate the multiple positive solutions for a boundary value problem of nonlinear impulsive fractional differential equations.The arguments are based upon the fixed point theorem of cone expansion and compression with norm type.
impulsive differential equation;boundary value problem;fractional derivative;fixed point theorem of cone expansion and compression with norm type
O 175.8 [学科代码] 110·54
A
(责任编辑:陶 理)
1000-1832(2015)03-0012-07
10.16163/j.cnki.22-1123/n.2015.03.004
2014-01-10
新疆维吾尔自治区自然科学基金资助项目(201318101-14).
张爱华(1984—),女,硕士,主要从事微分方程理论及其应用研究;通讯作者:胡卫敏(1968—),男,教授,主要从事微分方程理论及其应用研究.

