网络可靠性分析中自顶向下的二叉决策图构造研究

曾令国,潘竹生,莫毓昌

(浙江师范大学数理与信息工程学院,浙江金华321004)

网络可靠性分析中自顶向下的二叉决策图构造研究

曾令国,潘竹生,莫毓昌

(浙江师范大学数理与信息工程学院,浙江金华321004)

采用边界分区标识网络的思想,实现基于边界分区的自顶向下K端可靠度二叉决策图(BDD)构建算法。针对BDD构建过程中存在的节点冗余问题,提出无效边冗余消除和K点非连通冗余消除2种处理技术。在规则网络和实际工程中的实验结果表明,利用无效边冗余消除和K点非连通消除技术后的BDD改进算法,在不影响算法时间性能的情况下,可大幅缩减BDD尺度,提升K端网络可靠度分析算法性能,适用于大规模的网络可靠度分析。

网络可靠度;二叉决策图;边界集;边收缩;冗余

1 概述

网络技术便捷地实现了资源共享和信息交互,人们在享受这些便捷服务的同时,逐步意识到了网络可靠性的重要性,诸如通信网、互联网、电力网,更甚者如物联网、自来水供水网络等工程网络一旦出现故障,会影响到日常生活甚至让工作耽误,业务运作瘫痪。所以,对于网络可靠度的分析成为一个倍受关注的热点,建立高效的网络可靠性分析方法,确保网络可靠运行是现代工程网络研发和管理领域亟需解决的迫切问题[1]。

基于最小路集(或割集)[2]适用于小规模网络;文献[3]首先将分解理论用于可靠度计算中,文献[4]证明了当连接独立失效时,通过旋转和串并联概率消减,能生成分解算法的优化二叉结构,文献[5]表明结合消减技术如多边形链消减和串并联消减,分解算法能取得很好的性能,适用中等规模的网络,但该类算法存在无法高效操作大规模布尔函数和无法避免网络分解过程的同构冗余计算等问题,仍无法满足更大规模的网络可靠度计算需求;而文献[6]提出的以二叉决策图(Binary Decision Diagram,BDD)为基础的可靠度分析方法,即先用布尔路径函数等价刻画网络结构,再基于等价BDD分析路径函数得到网络可靠度,该方法利用了BDD操作大规模布尔函数的高效性性能上[7]。文献[8]提出了自底向上的二端可靠度和K端可靠度BDD分析算法;文献[9]利用边界集基于边收缩和边删除,提出了自顶向下的全端可靠度和K端可靠度BDD分析算法,并证明了这是到目前为止最为有效的BDD分析算法,但该算法没有很好地处理BDD节点的冗余问题,很大程度上影响网络可靠度分析性能。文献[10]采用边扩展技术识别了同构子图,消除了可靠度计算中的同构冗余。文献[9]消除了冗余节点型无效扩展路径和ST非连通型无效扩展路径,使整体性能提升90%以上。

本文采用边界分区Partition标识网络的思想,提出基于边界分区的自顶向下K端可靠度BDD构建算法。针对BDD构建过程中存在的节点冗余问题,给出无效边冗余消除和K点非连通冗余消除2种处理技术用于改进算法。

2 自顶向下的BDD构建

自顶向下BDD构建基于边收缩和边删除的网络分解,分解过程类似于构建一颗二叉树。为了提升算法性能,自顶向下算法利用Partition标识网络并用Hash实现子网共享。具体过程为:

(1)为原始网络G建立BDD节点,构建目标BDD的第1层节点,即根节点。

(2)从边序中按序取边ek。

(3)依次取上层BDD节点作为新根,并进行边收缩(生成边界分区ThenPart)和边删除(生成边界分区ElsePart)操作。分析边界分区 Partition特征,合理裁剪后为新根建立相应的左右分支。

(4)重复步骤(2)～步骤(3),直到BDD构建完成。BDD生成过程算法描述如下。

算法1自顶向下BDD生成算法

在BDD自顶向下构建过程中,可能出现K点一定连通或者一定不连通等状态。这些状态可在Partition的Append操作和Reduce操作过程中发现并识别。为了提升算法性能,当出现确定状态(连通或不连通)时,应及时裁剪并终止向下扩展。裁剪规则为:

(1)边界分区Partition Reduce操作时,如果出现带“∗”空block且未处理的K点数目＞0,则至少有1个K点被孤立,此时标记不连通,终止向下扩展。

(2)边界分区 Partition生成后,如果带“∗”block数目为1且未处理的K点数目==0,则所有K点在同一block中或不在block中的K点都有边连通于该block,此时标记连通,终止向下扩展。

3 性能改进

3.1 问题分析

观察图1的BDD,可以发现存在大量冗余BDD节点,冗余 BDD节点存在的原因:(1)无效边; (2)K点非连通。为了更好地说明这2种情况,设计示例网络如图2所示,带阴影节点为K点。

对这2种情况的详细说明如下:

(1)无效边,对某边分边正常和边失效2种情况进行边界分区生成,若得到相同边界分区,则该边为无效边。如图2(a)中的边2和边3。无效边的存在将导致大量冗余BDD节点生成,如图3(a)中的节点B2,B3和B4为冗余节点,占BDD节点总数的60%,严重影响BDD算法的分析性能。

(2)K点非连通,所谓K点非连通指的是K点分布于不同的连通分量中,如图3(b)所示,2个K点“0”和“5”分布于不同连通分量。对网络6-1(b)约定边序e1＜e2＜e3＜e4＜e5＜e6进行自顶向下BDD生成,结果如图3(b)所示。图中构建了4层BDD,生成了8个BDD节点,实际上在最高层构建B1节点时,2个K点“0”和“5”显然不能连通,不再需要向下扩展,从而可以避免冗余 BDD节点 Bi(i=1, 2,…,8)的生成。

图1 基于边收缩和边删除的自顶向下网络分解以及各层Partition

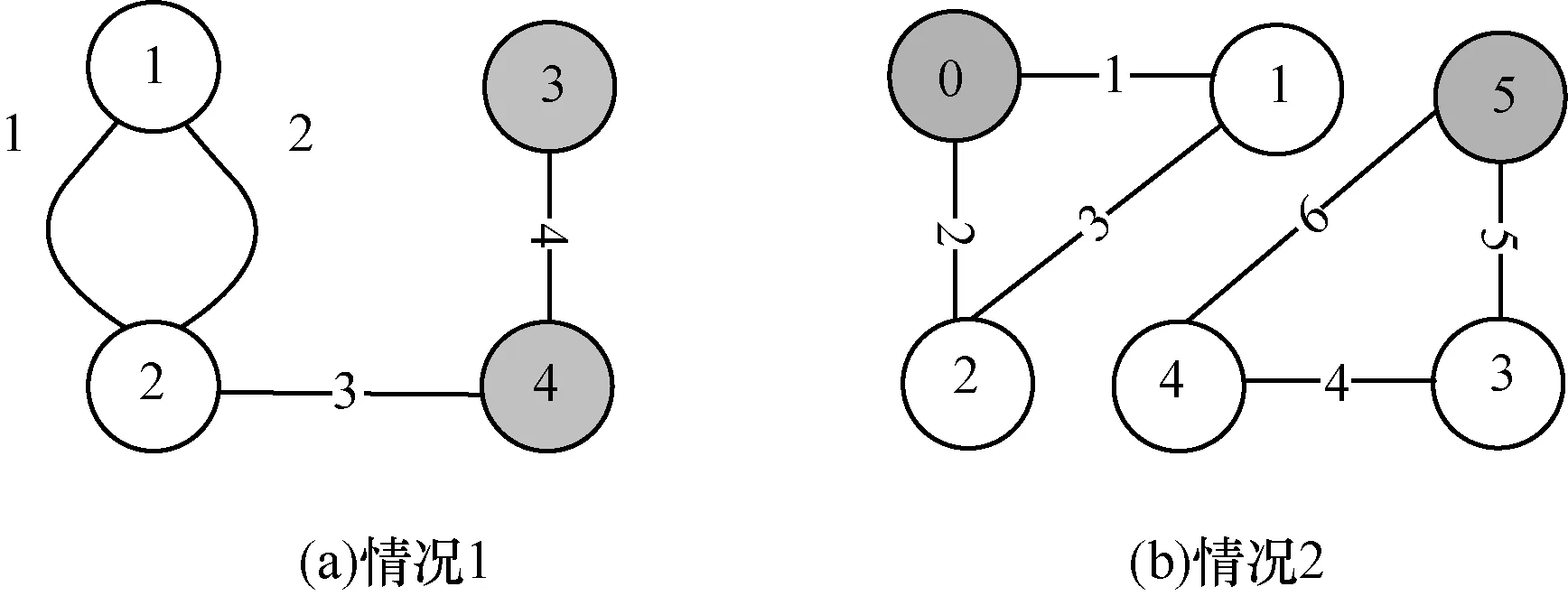
图2 示例网络

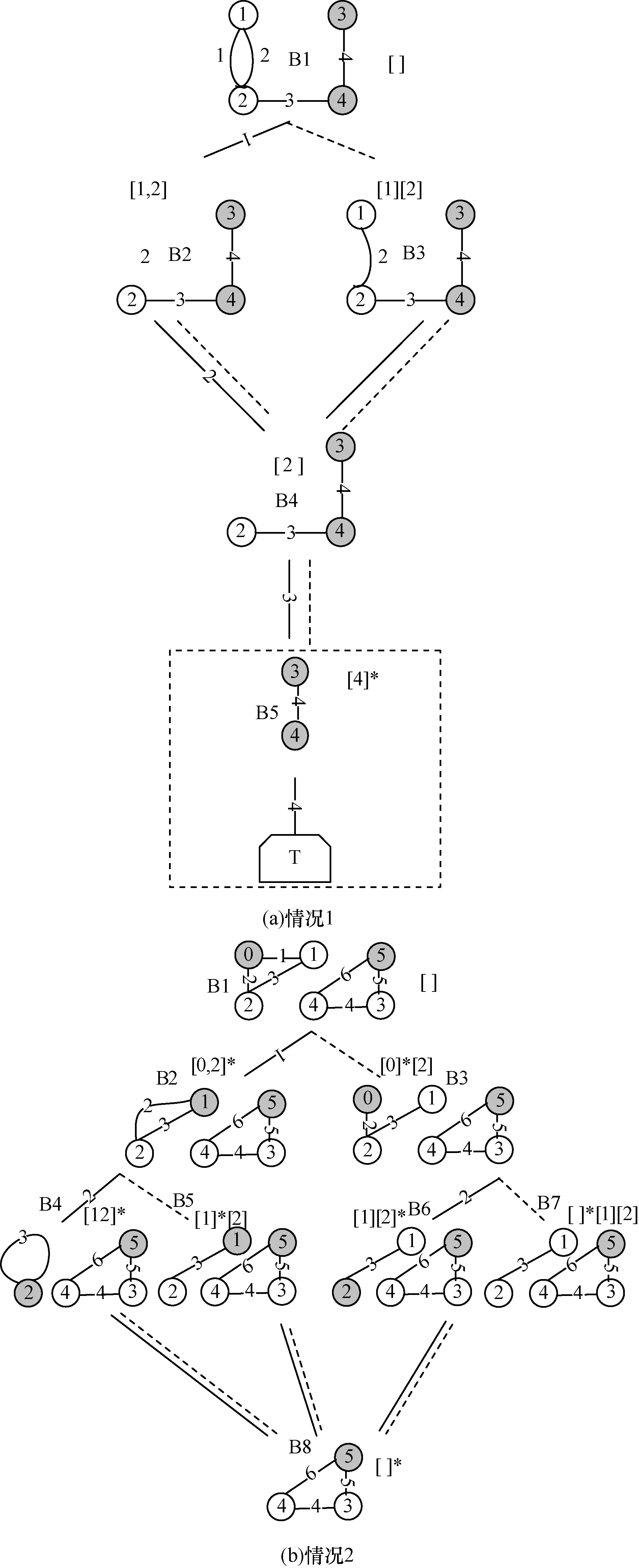
图3 自顶向下BDD生成

3.2 冗余消除

冗余消除分2类:无效边冗余消除和K点非连通消除。

(1)无效边冗余消除,其基本思想为:分析当前part,若边ek+1的2个端点u和v在part的同一block中,则边ek+1无效;如果其中有一端点在block中但不在新的边界分区中,|block|=1且该block不带“∗”,则边ek+1同样无效,删除无效边的具体算法如下。

算法2无效边冗余消除算法

图2(a)所示网络消除无效边e2和e3后,导致原本有效边e1变成无效边,进一步冗余消除后生成的BDD如图3(a)中虚线框所示,它只有一个BDD节点B5。

(2)K点非连通消除,根据定义非连通冗余消除问题转化为所有K点是否均可达问题。如果可达,则继续往下生成,否则标记不可达,终止往下生成,算法实现如下。

算法3K点是否可达算法

图2(b)所示网络由于K点不可达,经过非连通消除,直接返回不连通,不再往下生成BDD。

3.3 实验结果

为了更好地说明改进算法的性能,本文选用文献[9,11]中的基准网络,采用相同的广度优先边排序策略和边失效概率,测试网络可靠度Relib、算法运行时间time和BDD节点数目等指标数据。实验结果如表1所示,其中,Algo_Kuo和Algo_Hardy列数据来自文献[12],Algo_Original表示本文算法未带冗余消除时实验数据,InvalidEdgeE表示无效边消除后的实验数据,KNodeUnConE表示无效边和K点非连通都消除后的实验数据。

表1 二端可靠度实验结果

分析比较表1中的数据,改进算法增加2种冗余消除后,时间消耗增加不多,但BDD数目缩减32%以上,经过无效边消除,BDD数目和Kuo算法得到的实验结果相同;相比较Hardy算法实验结果,改进算法BDD数目减少25%以上,性能明显提升。

为了进一步考察2种冗余消除的性能,在N× N型网络(即每行每列都有n个节点构成的网络)中,随机选择ST点对并计算其二端可靠度,实验结果如表2所示。其中,S′为广度优先边排序的起点。综合分析表1和表2,得到汇总数据如表3所示。其中,time1和BDD1分别表示无效边冗余消除所增加的时间百分比和缩减的BDD节点数百分比;time2和BDD2分别表示在无效边冗余消除基础上,K点非连通冗余消除所增加的时间百分比和缩减的BDD节点数百分比。由表3得,无效边冗余普遍存在,经过消除时间消耗增加10%左右,BDD数目缩减28%以上;K点非连通冗余的存在性与网络结构和排序策略有关,在特定条件下如表3中6×6和7×7网络,K点非连通冗余消除能大幅缩减BDD数目以提升算法性能。

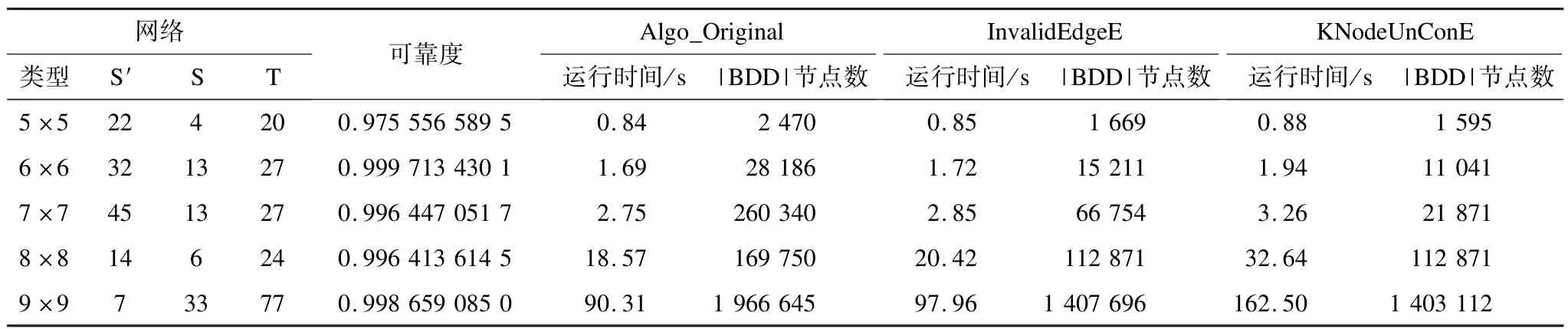
表2 N×N型网络二端可靠度实验结果

表3 网络可靠度性能指标数据

表4和表5为改进算法在K=|V|/2,K=|V|时的实验结果,其中,Algo_Improve列为2种冗余消除后的实验数据。

综合表1、表4和表5,取不同K值(K=2,|V|/ 2,|V|),考察消耗时间,Kuo算法在网络规模较大时迅速增加,Hardy算法和改进算法相对稳定;考察生成的BDD节点数目,Hardy算法普遍大于Kuo算法和改进算法,而后两者基本相同。

表4 K端可靠度实验结果(K=|V|/2)

表5 全端可靠度实验结果

综合以上实验结果,在K端可靠度计算中,Hardy算法优于Kuo算法,改进算法优于Hardy算法。随着无效边和K点非连通冗余的消除,改进算法能生成更简BDD,更适用大规模网络的可靠度分析。

4 案例应用分析

如图4所示为土耳其布尔萨市的配水网网络模型[13]。

图4 土耳其布尔萨市配水网络

图4中共有13个节点和18条边。假设所有节点都正常工作,且边失效相互独立(假设失效概率为0.1),采用BFS边排序策略,用改进的BDD方法来计算该网络的相关可靠度。

实验过程:首先随机选择ST点对,记录BDD尺度和BDD生成时间,计算二端可靠度值;其次随机选择K个节点,记录BDD尺度和BDD生成时间,计算K端可靠度值。实验按原始BDD方法、冗余边消除、K点非连通冗余消除、2种冗余同时消除4个步骤进行,实验结果如表6所示。

实验结果表明,改进算法应用于实际工程网络,能有效计算二端可靠度和K端可靠度。进一步分析表6中数据得表7和图5、图6。由表7所示,在实际的工程网络中,改进的算法充分识别并消除了无效边冗余和K点非连通冗余,在基本不增加时间开销的情况下,较大幅度地缩减了BDD尺度(15%左右),从而提升基于BDD网络可靠性方法的分析性能。

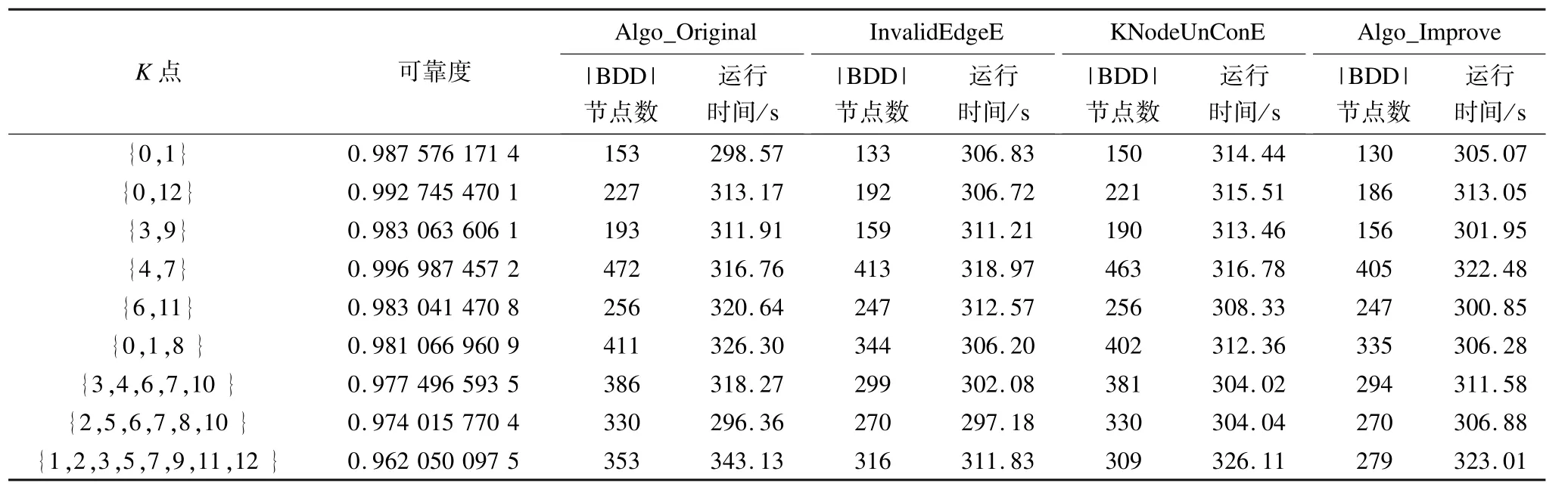
表6 冗余消除性能比较实验结果

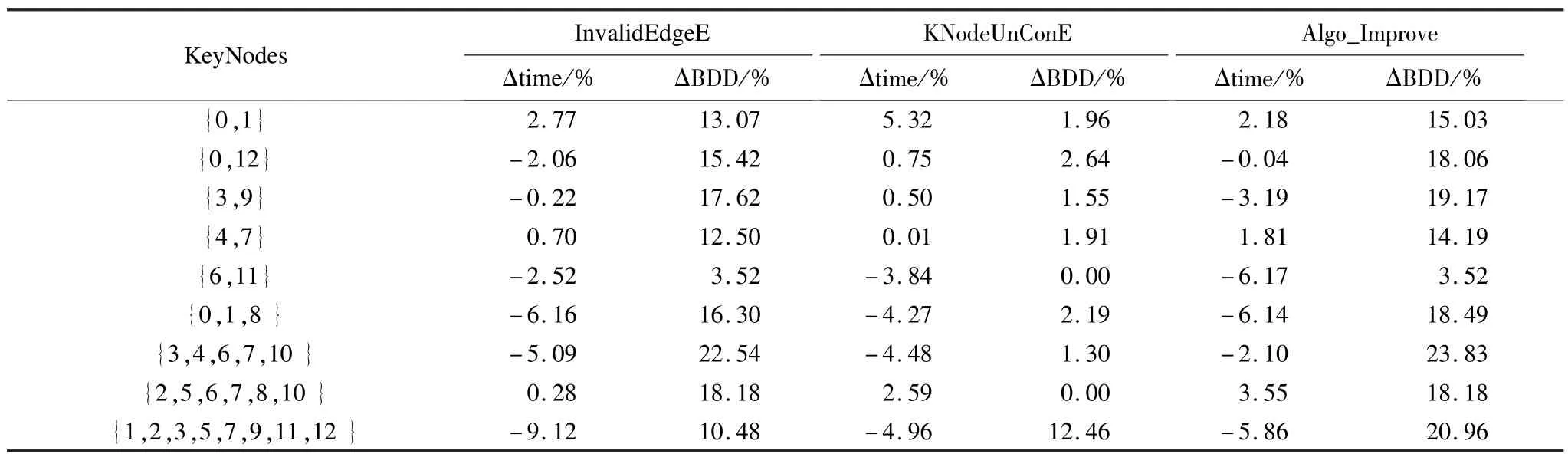
表7 KeyNods可靠度性能指标数据

图5为该工程网络考虑二端可靠度和K端可靠度时,在冗余消除前后的BDD尺度情况。由图5可得,2种冗余消除技术在不同程度上缩减了BDD尺度,联合2种消除技术后,大幅缩减了BDD尺度。图6所示为在考虑冗余消除时的时间开销情况。由图6可得,冗余消除前后,时间曲线交错分布,联合表7数据,整体而言,改进的算法时间成本有所减少。进一步分析表7中数据,一般情况下,在BDD尺度缩减上,应有3种冗余消除技术,有累加效果;在运行时间上,不会因为综合应用多种消除技术而增加。

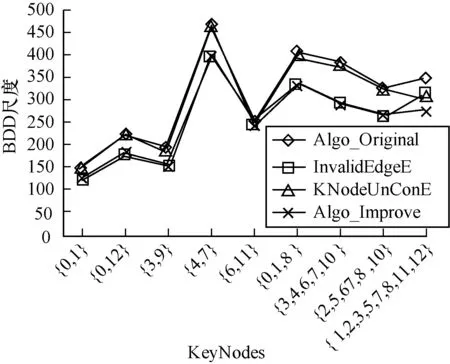
图5 BDD尺度比较

5 结束语

本文利用边界集思想,基于边收缩和边删除实现了自顶向下的K端可靠度BDD分析算法,深入分析其中的冗余BDD节点问题,提出并实现了无效边消除和K点非连通消除2种冗余消除技术。在规则网络和工程网络中的实验结果表明,带冗余消除的改进算法,在不增加时间成本的情况下,大幅缩减了BDD尺度,从而极大提升网络可靠度算法的分析性能,因此,更适用于大规模网络的可靠度分析。下一步研究工作为:(1)研究网络结构特征对BDD构建的影响,寻求更为高效的BDD生成方法;(2)研究边排序和网络结构与最简BDD的关系,设计更为合理的排序策略。

[1] 江光杰,李德毅.通信网可靠性评估[J].通信学报, 1997,18(8):85-89.

[2] Buzacott J A.The Ordering of Terms in Cut-based Recursive Disjoint Products[J].IEEE Transactions on Reliability,1983,32(5):472-474.

[3] Moskowitz F.The Analysis of Redundancy Networks[J]. AIEE Transactions on Communications and Electronics, 1958,77(5):627-632.

[4] Satyanarayana A,Chang M K.Network Reliability and The Factoring Theorem[J].Networks,1983,13(1): 107-120.

[5] Resende M.A Program forReliability Evaluation of Undirected Networks via Polygon-to-chain Reductions[J]. IEEE Transactions on Reliability,1986,35(1):24-29.

[6] Akers B.Binary Decision Diagrams[J].IEEE Transactions on Computers,1978,27(6):509-516.

[7] Dutuit Y,Rauzy A,Signoret J P.Computing Network Reliability with Réséda and Aralia[C]//Proceedings of European Safety and Reliability Association Conference. Berlin,Germany:Springer,1996:1947-1952.

[8] Yeh F M,Kuo S Y.OBDD-based Network Reliability Calculation[J].Electronics Letters,1997,33(9):759-760.

[9] Hardy G,Lucet C,Limnios N.Computing All-terminal Reliability of Stochastic Networks with Binary Decision Diagrams[C]//Proceedings of the 11th International Symposium on Applied Stochastic Models and Data Analysis.[S.l.]:IEEE Press,2005:1468-1472.

[10] 潘竹生,莫毓昌.网络可靠度BDD分析算法的性能改进[J].计算机工程与科学,2012,34(9):26-32.

[11] Yeh F M,Lu S K,Kuo S Y.OBDD-based Evaluation of k-terminal Network Reliability[J].IEEE Transactions on Reliability,2002,51(4):443-451.

[12] Hardy G,LucetC,LimniosN.K-terminalNetwork Reliability Measures with Binary Decision Diagrams[J]. IEEE Transactions on Reliability,2007,56(3):506-515.

[13] Selcuk A S,Yucemen M S.Reliability of Lifeline Networks with Multiple Sources Under Seismic Hazard[J].Natural Hazards,1999,21(1):1-18.

编辑 顾逸斐

Research on Binary Decision Diagram Construction in Top-down for Network Reliability Analysis

ZENG Lingguo,PAN Zhusheng,MO Yuchang
(College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China)

Using the boundary partition of identification network thought,the Binary Decision Diagram(BDD) construction algorithm in top-down K-terminal reliability based on boundary partition is realized.Aiming at the problem of node redundancy existed in BDD construction process,this paper proposes two processing techniques about invalid edge redundancy elimination and K-point nonconnected redundancy elimination.Experimental results of regular network and practical engineering show that,the improved BDD algorithm with invalid edge redundancy elimination technique and K point nonconnected redundancy elimination technique,can substantially reduce the BDD scale,and enhance the K-terminal network reliability analysis of algorithm performance,without affecting the time performance,which is applied to larger scale network reliability analysis.

network reliability;Binary Decision Diagram(BDD);boundary set;edge contraction;redundancy

1000-3428(2015)01-0309-07

A

TB114

10.3969/j.issn.1000-3428.2015.01.058

浙江省教育厅基金资助项目(Y201328293,Y201328072);浙江省重中之重学科开放课基金资助项目(ZSDZZZZXK24)。

曾令国(1979-),男,讲师、硕士,主研方向:系统可靠性计算;潘竹生,副教授、硕士;莫毓昌,副教授、博士。

2013-12-05

2014-03-12 E-mail:jk63@zjnu.cn

中文引用格式:曾令国,潘竹生,莫毓昌.网络可靠性分析中自顶向下的二叉决策图构造研究[J].计算机工程, 2015,41(1):309-315.

英文引用格式:Zeng Lingguo,Pan Zhusheng,Mo Yuchang.Research on Binary Decision Diagram Construction in Topdown Manner for Network Reliability Analysis[J].Computer Engineering,2015,41(1):309-315.