小型电力系统稳定性分析的改进算法及其应用
田 野,沈爱弟,王良秀,王 乐
(1.上海海事大学航运技术与控制工程交通行业重点实验室,上海201306; 2.中国船舶重工集团公司第七O四研究所,上海200031)
小型电力系统稳定性分析的改进算法及其应用
田 野1,沈爱弟1,王良秀2,王 乐2
(1.上海海事大学航运技术与控制工程交通行业重点实验室,上海201306; 2.中国船舶重工集团公司第七O四研究所,上海200031)
针对电力系统稳定性分析运算时间长、稳定域过于保守等问题,提出一种改进算法分析小型电力系统的暂态稳定性。基于能量函数法,利用平方和分解法得到李雅普诺夫函数,使用粒子群优化算法求其临界能量,改造李雅普诺夫函数扩张稳定域,以达到稳定域边界逼近实际边界的目的,采用Matlab对电力系统的稳定性进行仿真分析并验证其精确度及速度。应用改进的能量函数法实时判断当前状态的稳定裕度,计算故障极限切除时间,了解系统崩溃的接近程度。仿真结果表明,改进算法计算速度快、易于实现、可靠性高,具有较高的工程实用性。
电力系统稳定性;能量函数法;临界能量;粒子群优化;仿真分析
1 概述
现代电力系统是一个高维数、强非线性的复杂动力系统,其稳定性问题尤其重要。在陆上电力系统中,世界各地发生了多起由于电力系统失稳导致的大范围停电事故,这些事故造成了巨大的经济损失和社会影响,同时也反映出研究电力系统稳定的重要意义。
电力系统稳定性是指电力系统受到事故扰动后保持稳定运行的能力。目前暂态能量函数法的发展动态无外乎从提高计算速度和改善精度两方面进行理论和在线应用研究[1]。文献[2]提出了一种基于稳定域边界二次近似的算法并求取暂态电压稳定裕度指标,分析了考虑单负荷无穷大系统的暂态电压稳定性。文献[3]提出一种采用并联恒阻抗的负荷模型,并应用此模型进行了暂态电压稳定性判断。文献[4]建立以感应电机并联负载为基础的简化电力系统,并采用二阶正规型近似局部吸引域边界。
近二十年来,研究成果相当显著,计算速度比初期有了很大改善;求取的稳定域更加可靠,抑制了一定的保守性,暂态能量函数法进入电网稳定性分析等实际工程应用阶段。
本文研究适合电力系统典型结构的暂态稳定性分析方法,利用平方和分解法计算李雅普诺夫函数,并使用粒子群优化算法求出此函数的临界能量最优解,得到稳定域边界,改造李雅普诺夫函数对边界进行扩张,以逼近实际稳定域。根据系统实时配置情况,提出快速有效的电力系统实时安全裕度分析方法以及故障极限切除时间计算方法,最后使用Matlab仿真验证算法速度、精确度与正确性。
2 改进算法设计
随着电力系统的发展,其暂态稳定性越来越受到重视,由于时域仿真法计算量大、速度慢,且不能提供稳定裕度细节等原因,能量函数法在稳定性分析的工程应用方面占主导地位。
2.1 能量函数法
能量函数法的核心思想即不必求解微分方程,直接判断系统稳定性,在非零初始状态作用下的运动过程中,若能量随时间衰减以至最终消失,则系统迟早会达到平衡状态,即系统稳定。每个稳定的系统都有一个稳定域边界,在稳定域边界外的状态点会随着时间的增加而发散,在稳定域边界内的状态点会随着时间的增加逐渐逼近稳定平衡点。假设取某能量函数V(x),定义
2=5为稳定域边界,如图1所示。
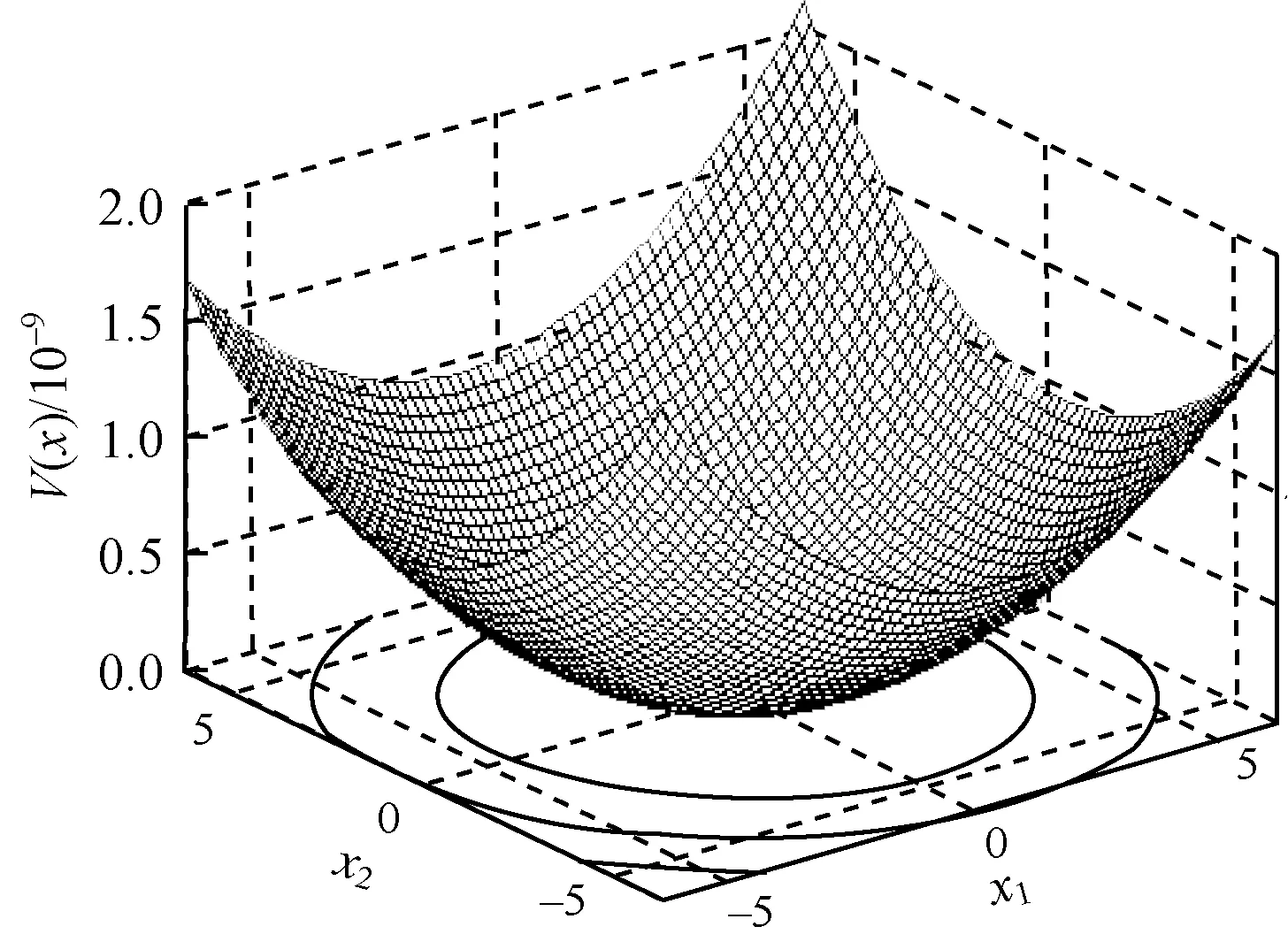
图1 能量函数介绍
在图1中,x轴y轴为状态变量,z轴为能量函数值,可以看出,随着状态点向外延伸,能量函数的值也随之增大,当能量函数的值超过临界能量时,系统将会失稳,而临界能量就是临界稳定域边界(x12+x2
2=5)上能量函数的值。
能量函数法主要流程为:首先能量函数法需构造一个目标系统的函数;其次判断此函数的导数为负定,即沿着目标系统运动时是否随时间的增长而衰减;接着计算临界能量,目标系统的稳定域边界就是此能量函数的某个等势面,其函数值即为临界能量;最后通过对状态点能量与临界能量的大小对比就能判断出状态点是否稳定。前两个步骤费时较多,但只需离线完成,使用本文的改进算法可大大提高计算速度,实时在线情况下,只需完成最后一步即可,可瞬间判断稳定性结论。
采用能量函数法进行暂态稳定分析的具体流程如图2所示。通过该流程可以看出,采用能量函数法进行暂态稳定分析的2个关键问题是:(1)能量函数(即李雅普诺夫函数)的构造与选择,在满足要求的情况下尽量选择逼近稳定域边界的函数;(2)临界能量最优解的计算,临界能量的计算实质是对稳定域边界近似基准点的计算。
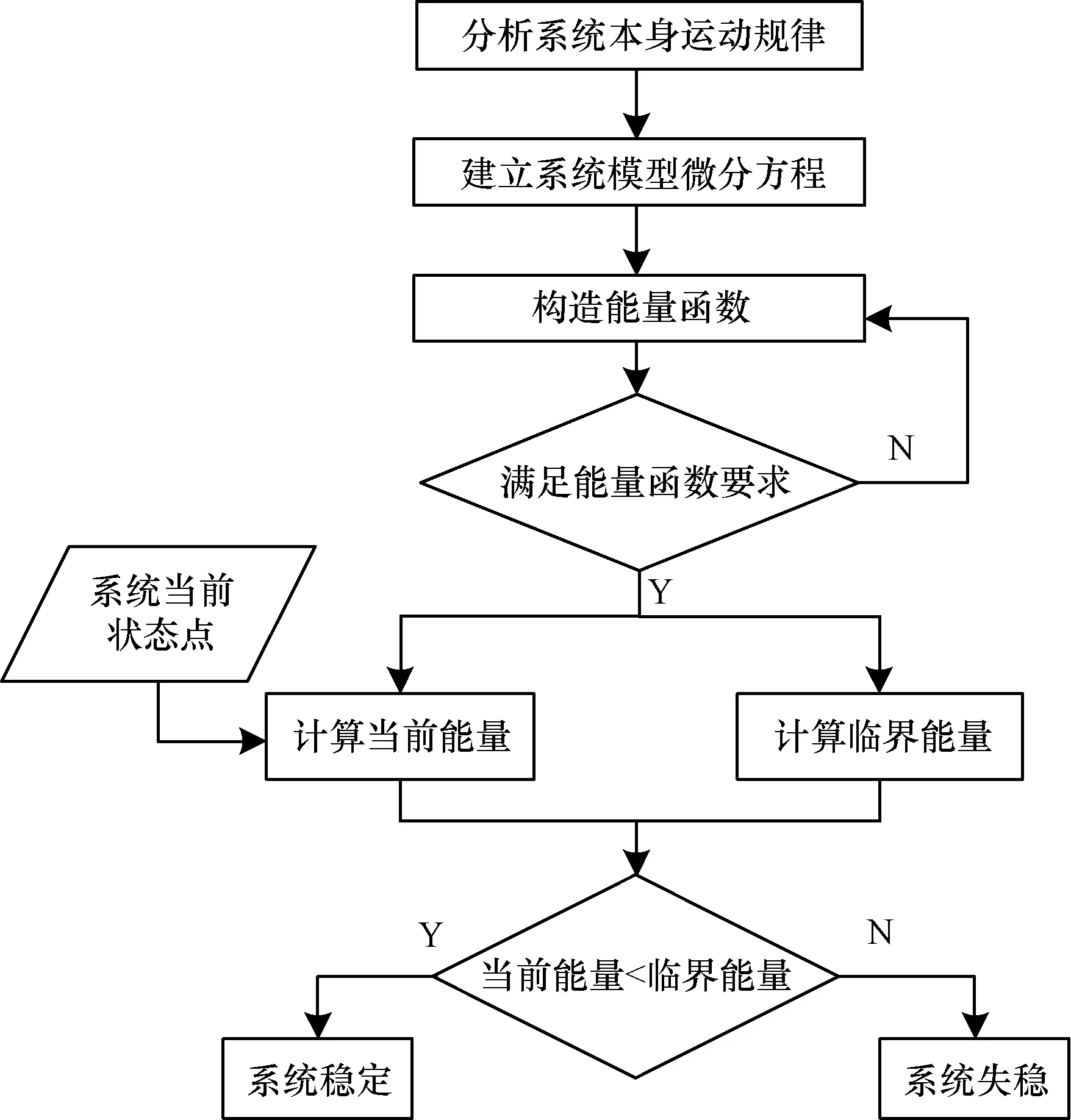
图2 能量函数法基本流程
2.2 平方和分解法
能量函数法的一个难点是能量函数的构造与选择,大部分李雅普诺夫函数对系统的适应性差,无法满足要求,要构造李雅普诺夫函数适应所有的系统比较困难。为此,在本文中采用基于平方和分解法自动计算李雅普诺夫函数,文献[5]证明此能量函数适用于所有多项式系统,计算量较小,但得到的稳定域具有一定的保守性,且非多项式系统须转化为多项式系统方可应用。首先给出李雅普诺夫函数的要求,需满足以下3点,即李雅普诺夫定理:
定理1李雅普诺夫定理
(1)V(x,t)正定且有界,β(‖x‖)≥V(x,t)≥α (‖x‖)>0;
(2)(x,t)负定且有界,(x,t)≤-γ(‖x‖)<0;
(3)‖x‖→∞,则V(x,t)→∞。
所包含的3个条件对于高于四阶的多项式系统是非常苛刻的,想要获得满意的稳定域边界更加困难。一个检验多项式非负的充分条件是它满足平方和分解,,得到以平方和表示的李雅普诺夫函数,本文中将分别采用多种平方和能量函数验证算法的正确性。
2.3 粒子群优化算法
能量函数法的另外一个难点是临界能量的求取,以往的能量函数法一般采用遗传算法(GA)求取临界能量的最优解[6],但是遗传算法收敛速度慢、参数复杂等缺点限制了它的发展,在本文中将采用粒子群优化算法代替遗传算法进行最优解的求取。
此算法具有自我学习提高和向他人学习的双重优点,从而能在较少的迭代次数中找到最优解,大大减少了计算时间,其概念简单、易于实现,同时又有深刻的智能背景,既适合科学研究,又特别适合工程应用[7]。
其大致步骤可分为5步[7-8],如图3所示:
(1)设定粒子位置的上下限,并随机初始化粒子群中每个粒子的位置和速度。
(2)根据系统方程计算每个粒子的适应度。
(3)记录粒子计算过具有最好适应度的位置(个体最优解),并记录群中所有粒子计算过的最好位置(全局最优解)。
(4)依据公式:

对粒子的速度和位置进行优化。其中,xij表示群体中i粒子的位置为j;vij是它对应的速度;ω为惯性权重;c1,c2为加速度常数(学习速率);r1,r2为[0,1]均匀分布的随机数,式(1)也是粒子群优化算法的核心。
(5)结束条件为:全局最优解的适应度满足要求或达到设定的迭代次数,否则返回步骤(2),重新计算此流程。
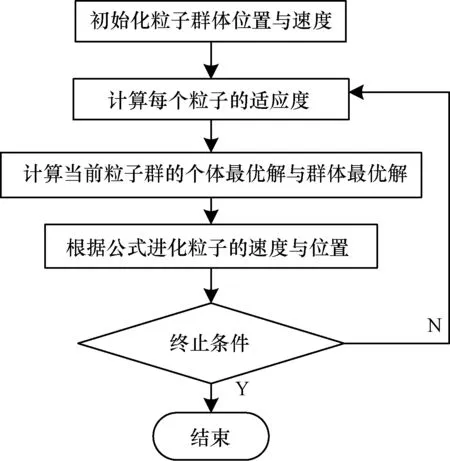
图3 粒子群优化算法流程
2.4 稳定域的扩张
由于能量函数法的特性,函数的形状不可能完全拟合实际稳定域边界,即使是采用粒子群优化算法计算出的临界能量,计算得来的稳定域边界也常常显得保守。本文采用后向欧拉积分法[9]对李雅普诺夫函数进行改造,以对稳定域边界扩张,减小保守性,得到的结果令人满意。
如图4所示,最内层的为初始能量函数稳定域,中心为稳定平衡点,中间层为扩张能量函数稳定域,最外围的是实际稳定域。使用文献中的扩张法,通过逆向时间积分将状态点向外扩张,将稳定域逐渐扩大,理论情况下能完全逼近实际稳定域。
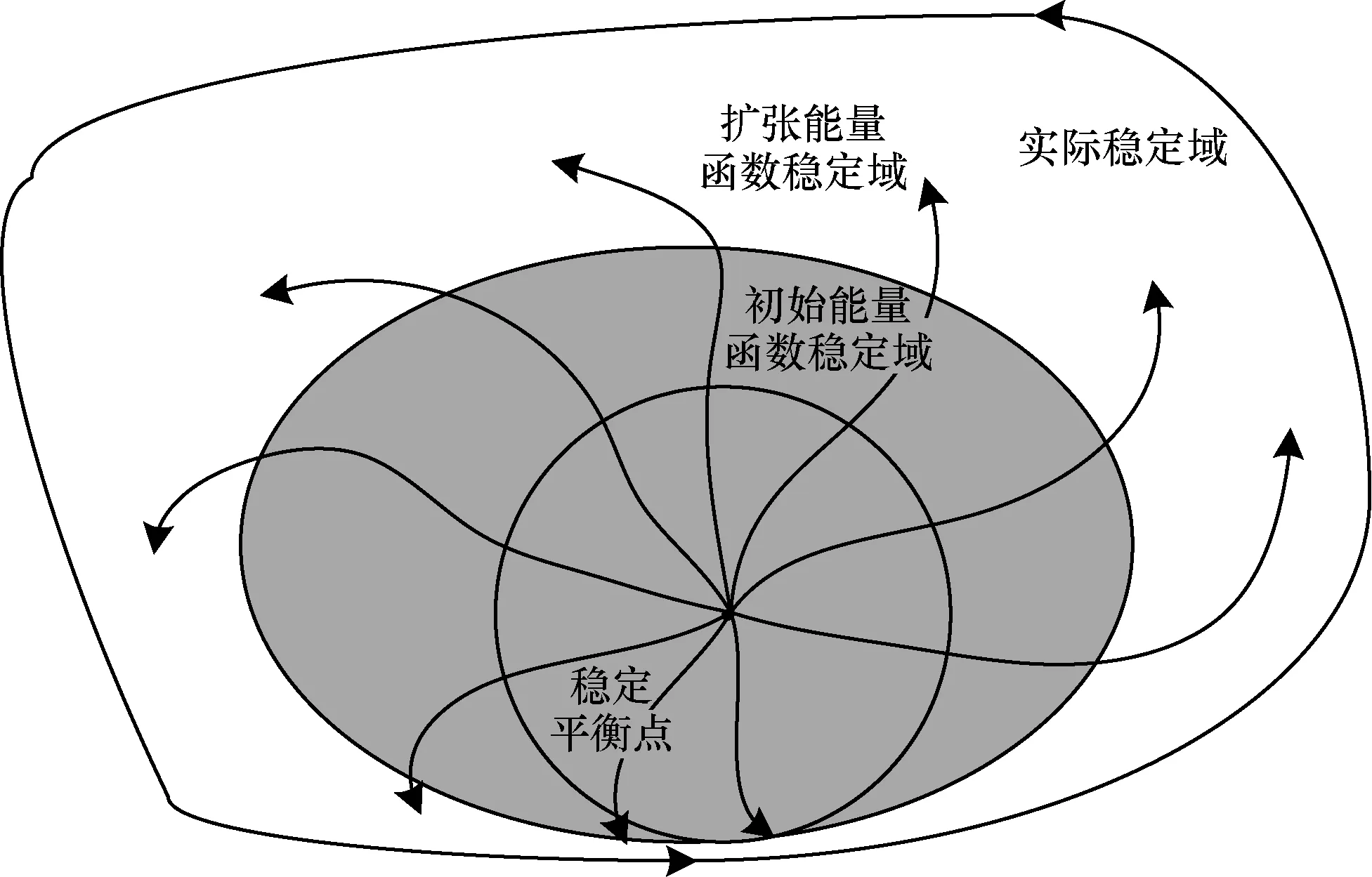
图4 能量函数扩张示意图
算法实际上是能量函数沿系统积分曲线扩张的近似,考虑各类算法的计算量和精确性,采用后向欧拉积分的能量函数扩张算法。对非线性系统的能量函数V(x),构造如下的迭代序列:

其中,d为迭代步长;k为迭代次数。
此算法既是在足够小的迭代步长下,用d×f(x)来代替很小一部分积分曲线,通过多次迭代扩展到一个较大部分,稳定域边界得以扩张,故d的选取要适当小,但太小则不能体现出扩张效果,另一方面,由于积分过程的收敛性限制,参数d不能选得太大,因此需要的扩张迭代次数k要尽可能大,但会影响运算速度,根据仿真经验可求得满意的k值。
2.5 算法总结
在工程应用中一般计算不出整个稳定域,也无需求出,判断状态点是否在稳定域边界内即可。实时判断当前状态的稳定裕度,计算故障极限切除时间[10],了解系统对崩溃的接近程度是十分重要的,如图5所示为大扰动下系统稳定裕度k与故障极限切除时间t的算法流程图,其总结了上述所有算法。在系统稳定的情况下当k越接近1,稳定裕度越大,即离系统崩溃越远。

图5 大扰动下的算法流程
3 系统模型的建立
本文使用简化的三机系统以及电力系统综合模型这2种经典的系统模型来验证改进算法的正确性。此2种模型均大量被其他文献引用验证,具有一定的参考性。
3.1 简化的三机系统
此系统作为常用的电力系统模型被广泛应用于稳定性研究中[11-12],因为其拟稳定域边界可近似求出,并能作为真实稳定域边界[12],所以将其作为验证稳定性分析方法精确度的简单系统。并且由于这是二维系统,便于观测稳定域的图形,以达到视觉上的直观对比。简化三机系统模型如式(3)所示[11]:

使用平方和分解法求李雅普诺夫函数V(x)的前提条件是多项式系统。此非多项式系统包含三角函数,需进行多项式转化才得以求得李雅普诺夫函数,系统稳定平衡点为xsep(0.028 01,0.064 03),通过泰勒公式式(4)将系统方程在平衡点进行二次展开:
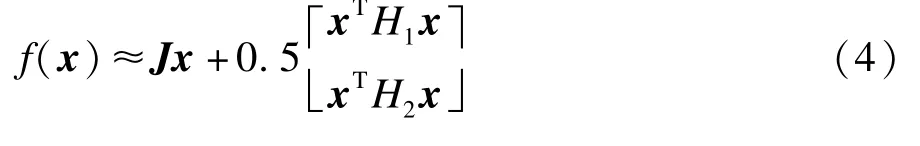
为验证分析方法的精确度,需与实际稳定域作比较,而高阶系统的实际稳定域一般极难得到,而对于简化的三机系统,能通过以下定理得到系统实际稳定域[12]:
定理2若系统存在能量函数,其渐近稳定平衡点xsep所对应的拟稳定域边界∂S(xsep)由边界上I型不稳定平衡点的稳定流形的闭包组成。
所谓I型不稳定平衡点即系统雅克比矩阵J=有1个正实部特征值。此系统中所有5个不稳定平衡点均为I型不稳定平衡点,所以在系统的所有平衡点中选取不稳定平衡点为起始点对系统做逆向时间积分,在Matlab中用ode45函数就能快速完成,即可得到拟稳定域边界,并判断此边界是否为闭包,这可以近似看作系统的实际稳定域边界以验证研究的精确度。
3.2 综合电力系统模型
综合电力系统模型是所有电力系统模型的基础,由原动机-PI调速器、同步发电机、PI励磁系统和恒功率负载组成,发生扰动(如三相接地短路故障),一段时间内恢复正常。
系统模型如图6所示。

图6 综合电力系统模型
原动机-PI调速器:
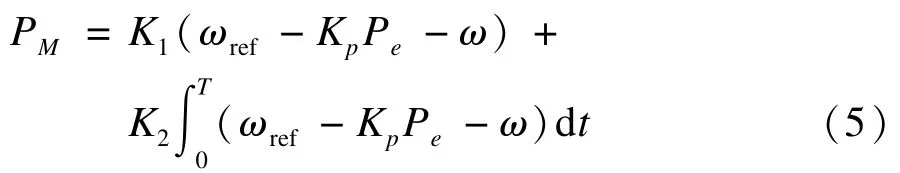
其中,PM为机械功率;K1,K2为PI系数;ωref为给定转速;Kp为有功功率下垂系数;Pe为有功功率,令:

则公式化为式(7):
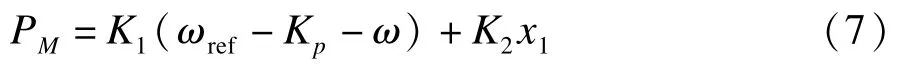
同步发电机三阶模型:
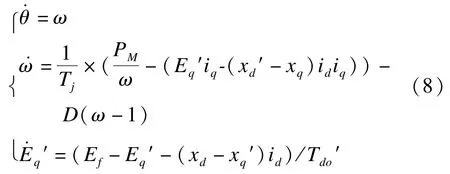
其中,θ为机械角度;Tj为惯性系数;Eq′为q轴暂态电势;id,iq为dq轴电流;D为摩擦系数;xd,xd′,xq,xq′为dq轴电抗和暂态电抗;T′do为开路暂态时间常数。
PI调节励磁系统:
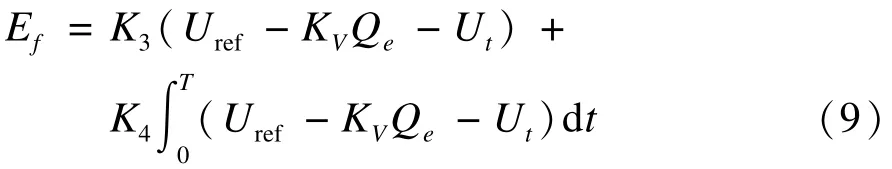
其中,Ef为励磁电压;K3,K4为PI系数;Uref为给定电压;KV为无功功率下垂系数;Qe为无功功率;令:

则公式化为式(11):

将式(5)、式(7)、式(8)、式(11)联立即得到完整的综合电力系统模型。
4 仿真与分析
根据上述系统模型与算法流程,采用Matlab对简化的三机系统以及综合电力系统模型进行仿真以验证算法的正确性及精确度。
通过多次仿真结果发现,粒子群个体数目选为50,迭代次数为50比较合适,不仅提高了精确度,而且保证了速度优势。通过多次仿真结果发现,当采用改进李雅普诺夫函数法进行边界扩张时,d取0.1,k取5(即迭代5次),取此值时稳定域达到一定的扩张,且并不过多影响运算速度。
对于简化三机系统模型取文献[11]的能量函数及临界能量作为比较,其能量函数为式(12):
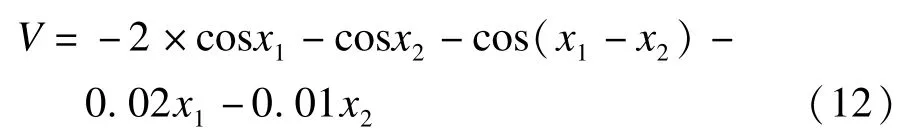
图7~图9为三机系统采用2次、4次、6次李雅普诺夫函数估计的稳定域边界与真实稳定域边界的对比,4次和6次因函数过长,这里不再列出,2次能量函数为式(13):


图7 2次李雅普诺夫函数稳定域边界对比
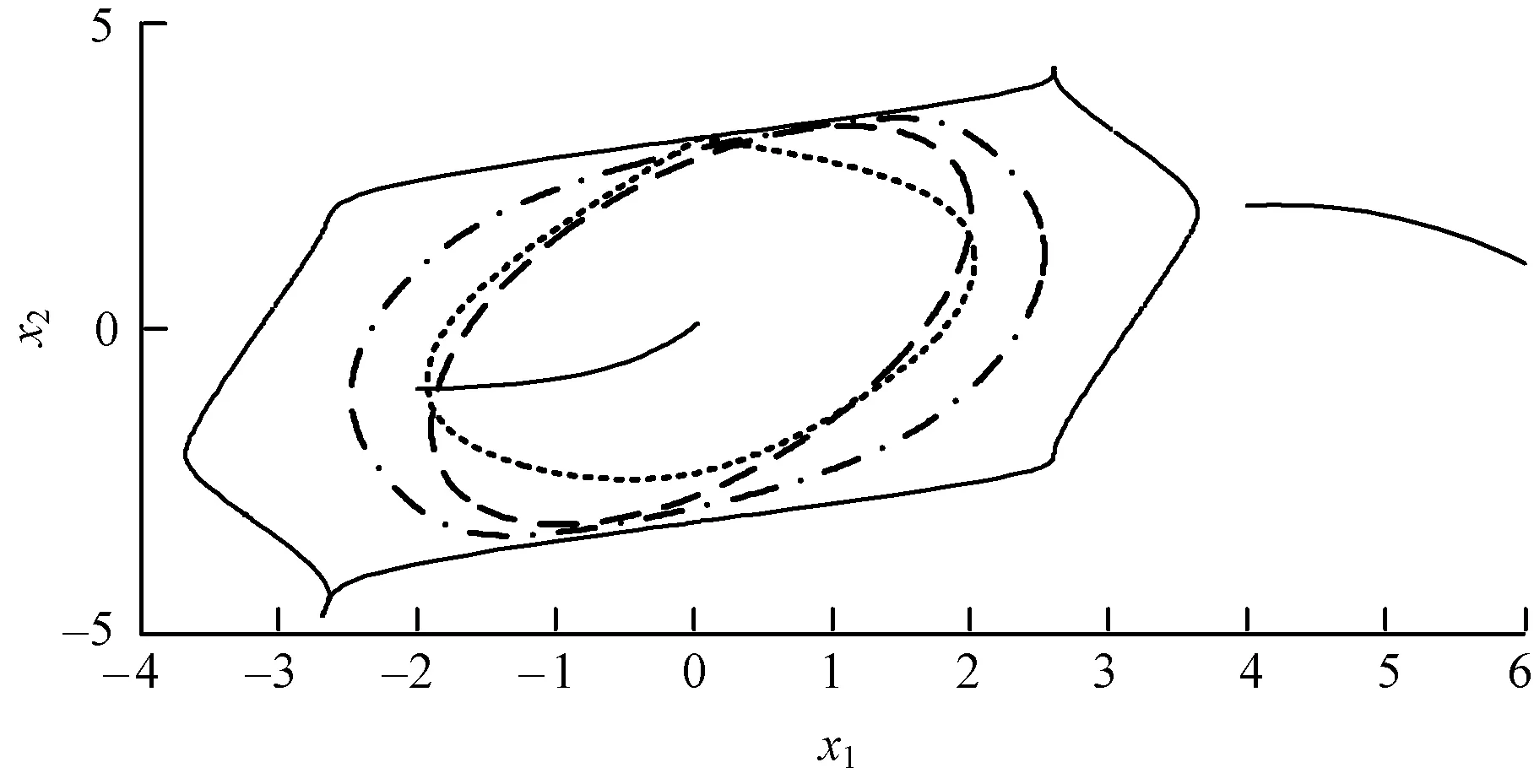
图8 4次李雅普诺夫函数稳定域边界对比
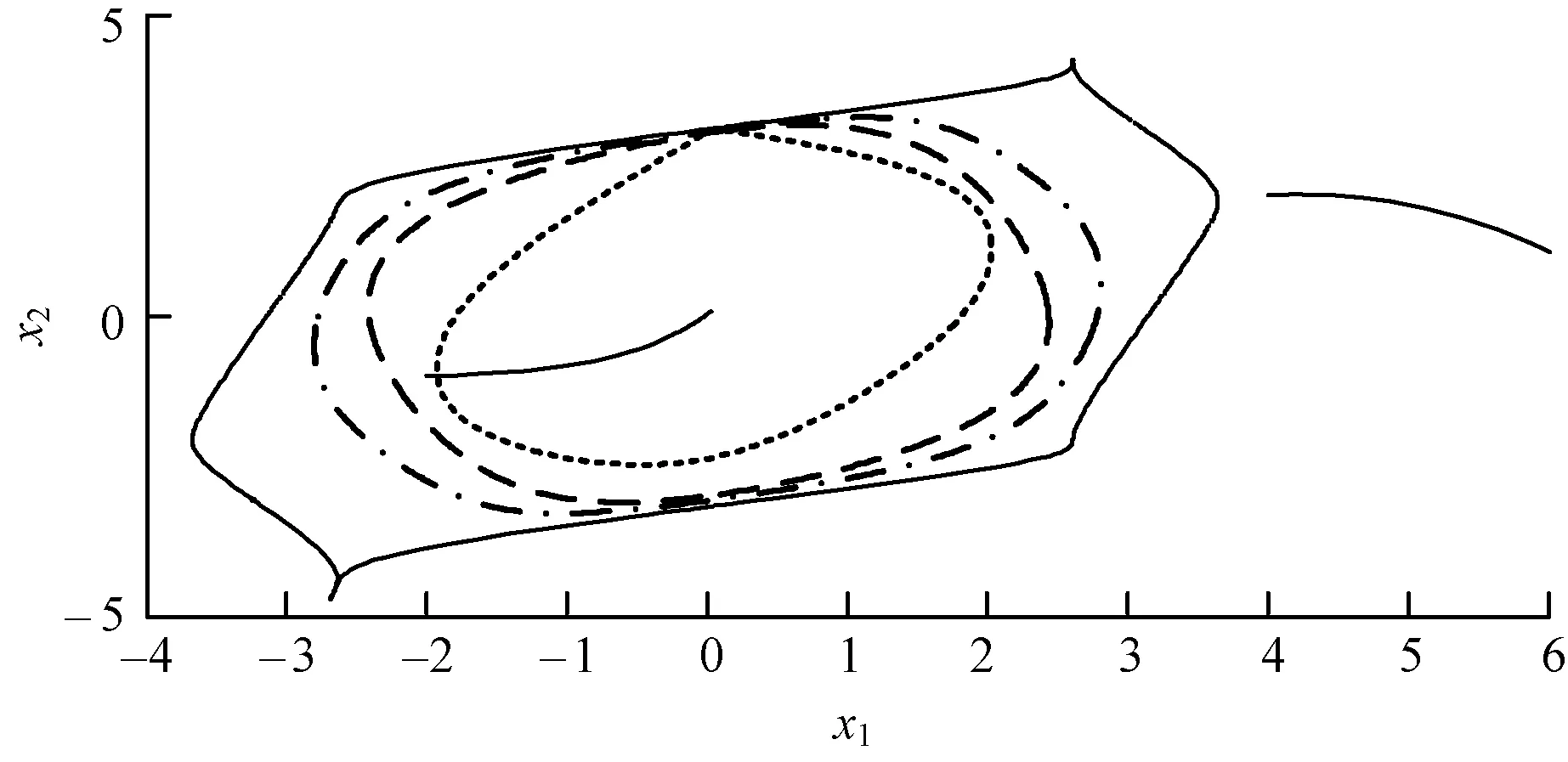
图9 5次李雅普诺夫函数稳定域边界对比
图中实线代表实际稳定域边界,即是由逆向时间积分求得的拟稳定域边界;点线代表原始能量函数得到的稳定域边界[12];划线代表粒子群优化算法得到的稳定域边界;点划线代表使用粒子群优化算法后并对李雅普诺夫函数进行改造得到的扩张稳定域,即使用改进能量函数法得到的稳定域。图中粗线分别给出了系统在不同初值(-2,-1)和(4,2)时,状态变量的时域变化曲线。当状态点在实际稳定域边界外,运行点发散,系统失稳,而当状态点在实际边界内时,运行点逐渐向平衡点收敛,系统稳定。这说明了所求的实际稳定域与通过改进能量函数法计算得出的稳定域均是有效的。
假设系统实际稳定域面积为1,通过图7~图9计算各算法得到的稳定域边界面积,可观察各算法的保守性,如表1所示。

表1 稳定域面积比较
由图7~图9以及表1可看出,传统稳定域远小于PSO稳定域,而改进能量函数法得到的稳定域更为扩张;2次以及6次函数得到的稳定域较好地抑制了保守性,达到实际稳定域的约80%,6次函数为最优;而4次函数效果较差,仅比传统算法略好。
为在数值上直观比较各方法的精确度,使用2.5节的算法在状态点[-2,-1]对系统的稳定裕度进行计算,如表2所示。

表2 状态点[-2,-1]稳定裕度比较
由表2能看出,由于选取的状态点均临近稳定域边界处,传统函数算法对此状态点的稳定判断错误,而改进算法中6次函数得到的稳定裕度更接近1,优于2次函数及4次函数的结果,改进算法优于未使用此方法的结果,6次改进算法得到的结果最优。故障极限切除时间因在此系统中无法给出故障方程,没有比对意义,这里不作计算比较。
图10为2次改进算法在状态点横坐标在区间[-4,4],纵坐标在区间[-5,5]内得到的稳定裕度。可以看出当状态点超出预定范围,稳定裕度为0,即此时系统失稳,而系统稳定裕度最佳状态点在中心部分,有且仅有一点,稳定裕度值为1。

图10 二次改进算法稳定裕度
表3为各算法的计算时间,由于系统较小且设定了较大的迭代次数以确保临界能量值为最优,因此遗传算法与改进算法的计算时间差距较小;但达到误差小于1%的临界能量最优值时,遗传算法用时约30 s,粒子群优化算法仅需约16 s,大大减少了计算时间。传统算法由于参考了文献中的数值和函数,计算时间无法给出。

表3 各算法稳定性计算时间比较 s
纵观本文系统所有的仿真结果,改进算法较传统算法和大部分优化算法相比运算速度上有明显优势,且较好地抑制了保守性,易于实现,收敛速度快,可靠性高,稳定域边界基本满足要求。
随后针对综合电力系统模型进行分析,应用本文算法求得2次能量函数为:

计算得系统在能量函数下的临界能量为3.787 1;随后进行能量函数稳定域扩张,即可代入当前状态点求得当前能量并与临界能量比较,并求取稳定裕度。
发电机稳定运行下,突加恒功率负载,当机端电压小于0.8 pu时,视为系统失稳。此时状态变量为[1,1.01,-0.01,-0.01],代入能量函数得到此时的能量为1.901 9<3.787 1,稳定裕度为0.497 8。由于系统稳定裕度在[0,1]之间是稳定的,可见实验系统是稳定的,且稳定裕度比较大,即与1比较接近。
再分析短路故障下的稳定情况,当系统带负载稳定运行后,发生三相短路接地故障,此瞬间的状态变量为[0.99,0,-0.01,-0.01],此时稳定裕度为4.698 7>3.787 1,系统失稳,使用2.5节中的算法计算得到极限故障切除时间为0 s,即由于是单台发电机组带负载运行,在发生三相短路故障时,因没有冗余电能拖动负载,系统当即失稳,电压跌落至0,计算结果与情况相符。
通过Simulink仿真验证可得到相同结论,如图11波形所示,波形为发电机稳定运行后1 s突加0.5 pu的恒功率负载,系统稳定运行,电压有小幅跌落。于1.5 s发生三相接地故障,且于1.6 s切除故障,系统期间电压已低于0.8 pu,说明已失稳,再次验证了结论的正确性。
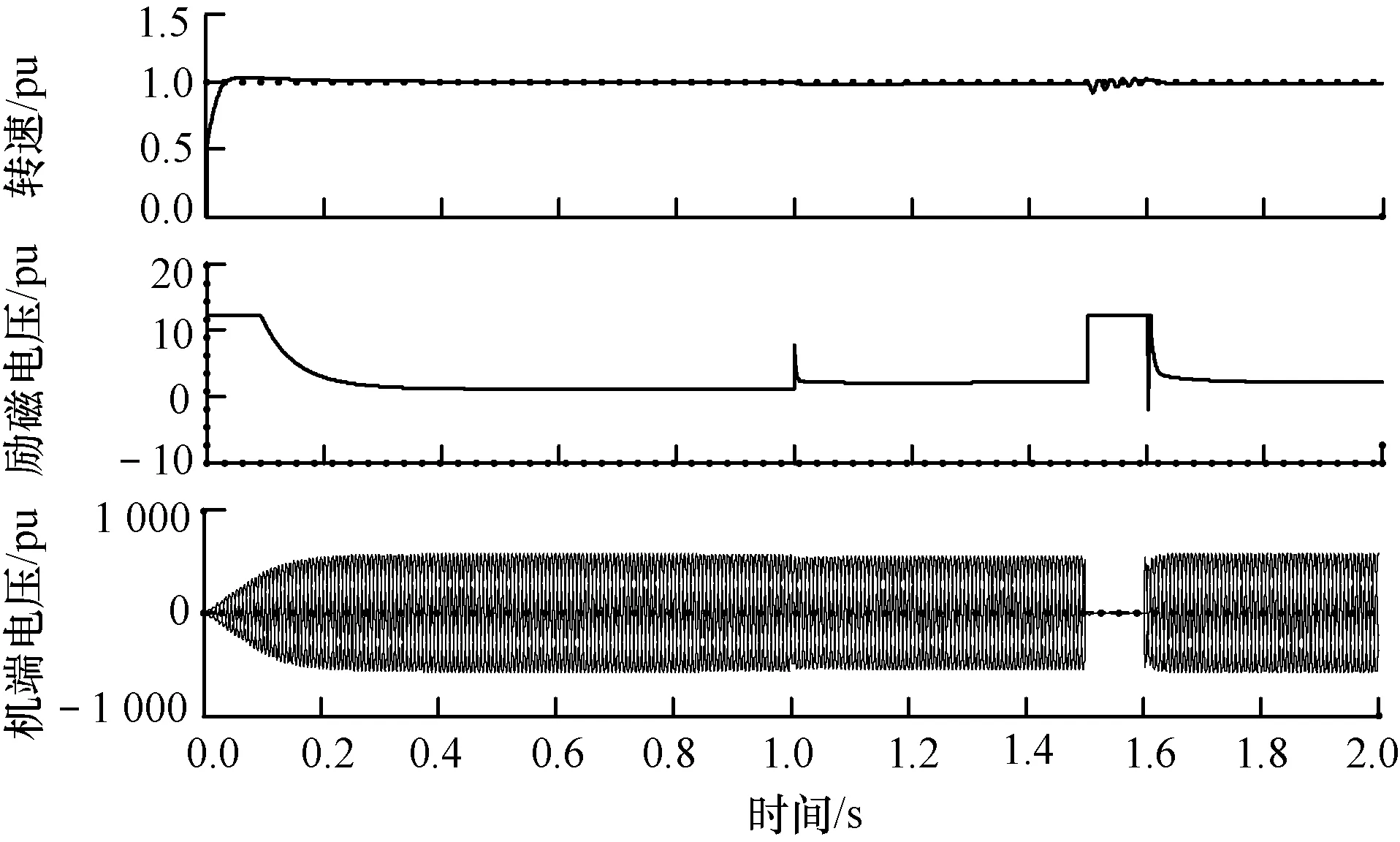
图11 系统仿真波形
在2个不同系统中运用本文算法得到的结论与仿真实验结论一致,验证了所提算法的正确性。而且,此方法在线计算时间非常短,并抑制了保守性,可以满足工程需要。
5 结束语
本文提出一种基于粒子群优化算法的改进算法,将稳定域边界近似计算应用于暂态稳定问题的分析。通过对简单系统中的仿真,可得到如下结论:
(1)该算法继承了李雅普诺夫直接法的优点,计算速度快,能提供稳定裕度细节等。
(2)结合了粒子群优化算法和稳定域扩张法的综合算法,与传统算法相比,在求解稳定域边界时,计算速度上有着较大的优势,且较好地抑制了稳定域的保守性,易于实现,可靠性更高,稳定域边界实现一定的扩张。
(3)以此算法为基础,对于改变工况时的系统稳定指标和故障极限切除时间提出了较为全面的算法流程,适用于大部分系统,具有较好的工程实用性。
系统稳定性分析对于电力系统有着重要意义,将本文改进算法应用于电力系统是未来研究的方向。
[1] 王 川.负荷冲击型大扰动下船舶综合电网暂态电压稳定性研究[D].大连:大连海事大学,2012.
[2] 王义红,梅生伟.基于稳定裕度指标的暂态电压稳定分析[J].电工电能新技术,2007,26(2):39-44.
[3] 林舜江,刘杨华.简单电力系统暂态电压稳定的直接分析法[J].湖南工业大学学报,2011,25(1):70-76.
[4] 林舜江,李欣然,刘杨华,等.考虑负荷动态模型的暂态电压稳定快速判断方法[J].中国电机工程学报, 2009,29(4):14-20.
[5] Chiang H.Network Reduction BCU Method and Its Theoretical Foundation[M].[S.l.]:IEEE Press,2011: 235-253.
[6] Tan W,Packard A.Stability Region Analysis Using Polynomial and Composite Polynomial Lyapunov Functions and Sum-of-Squares Programming[J].IEEE Transactions on Automatic Control,2008,53(2): 565-571.
[7] 吴建生,秦发金.基于Matlab的粒子群优化算法程序设计[J].柳州师专学报,2005,20(4):103-106.
[8] 杨淑莹.模式识别与智能计算——Matlab技术实现[M].北京:电子工业出版社,2008.
[9] Liu Feng,Wei Wei,Mei Shengwei.On Expansion of Estimated Stability Region:Theory,Methodology,and Application to Power Systems[J].ScienceChina Technological Sciences,2011,54(6):1394-1406.
[10] 薛安成,沈 沉,梅生伟.基于稳定域边界理论的暂态稳定指标及其应用[J].电力系统自动化,2006, 30(8):1-6.
[11] Chiang Hsiao-Dong,James S.Thorp Stability Regions of Nonlinear Dynamical Systems:A Constructive Methodology[J].IEEE Transactions on Automatic Control, 1989,34(12):1229-1241.
[12] Chiang H D,Hirsch M,Wu F F.Stability Regions of Nonlinear Autonomous Dynamical Systems[J].IEEE Transactions on Automatic Control,1988,33(1):16-27.
编辑 顾逸斐
Improved Algorithm of Stability Analysis in Small Power System and Its Application
TIAN Ye1,SHEN Aidi1,WANG Liangxiu2,WANG Le2
(1.Key Laboratory of Marine Technology and Control Engineering,Ministry of Communications, Shanghai Maritime University,Shanghai 201306,China; 2.704 Institute,China Shipbuilding Industry Corporation,Shanghai 200031,China)
This paper proposes an improved algorithm to solve the stability analysis problems of long computing time and too conservative stability ragion in small power system,such as the long time in computing,too conservative issues and so on.The algorithm is based on energy function.Use squares decomposition method to obtain Lyapunov function and use Particle Swarm Optimization(PSO)algorithm to get critical energy.Transform the Lyapunov function expand stability field in final.The algorithm can achieve stability boundary approximation of the actual boundary.Then stability of the power system is simulated and analyzed in Matlab to verify its accuracy and speed.Application of improved energy function method can determine the current state’s stability margin in real-time,calculate limited clearing fault time and understand how close the system crash is.The improved algorithm is fast to calculate,easy to achieve,and has higher reliability and better project practicality.
power system stability;energy function method;critical energy;Particle Swarm Optimization(PSO); simulation analysis
1000-3428(2015)01-0296-07
A
TP301.6
10.3969/j.issn.1000-3428.2015.01.056
科技部2012年度国际科技合作与交流专项基金资助项目“船舶电能质量监测与谐波滤除关键技术合作研究”(2012DFG 71850);科学技术委员会地方院校能力建设专项基金资助项目“船舶电力推进系统故障诊断与安全控制技术研究及应用”(11170501700)。
田 野(1990-),男,硕士,主研方向:系统分析;沈爱弟,高级工程师;王良秀、王 乐,工程师。
2014-03-05
2014-04-03 E-mail:tykram0821@hotmail.com
中文引用格式:田 野,沈爱弟,王良秀,等.小型电力系统稳定性分析的改进算法及其应用[J].计算机工程,2015, 41(1):296-302.
英文引用格式:Tian Ye,Shen Aidi,Wang Liangxiu,et al.Improved Algorithm of Stability Analysis in Small Power System and Its Application[J].Computer Engineering,2015,41(1):296-302.

