一种基于MapReduce的短时交通流预测方法
梁 轲,谭建军,李英远
(1.中国科学院广州地球化学研究所,广州510640;2.中国科学院大学,北京100049; 3.广州中科盛博信息技术有限公司,广州510630)
一种基于MapReduce的短时交通流预测方法
梁 轲1,2,谭建军1,李英远3
(1.中国科学院广州地球化学研究所,广州510640;2.中国科学院大学,北京100049; 3.广州中科盛博信息技术有限公司,广州510630)
非参数回归方法是短时交通流预测常用的方法,但现有非参数回归方法存在预测速度与精度之间的矛盾。为此,提出一种适用于海量历史数据、基于MapReduce与遗传算法的非参数回归短时交通流预测方法。通过引入MapReduce并行计算框架,加快K最近邻算法的搜索速度。在数据预处理阶段利用遗传算法优化关键参数的设置,并采用MapReduce加速参数优化过程,以解决遗传算法迭代运算时间长的问题。实验结果表明,该方法在保证交通流预测精度的前提下,明显提高了预测速度,并且具有较好的可伸缩性。
交通流预测;非参数回归;K最近邻搜索;遗传算法;MapReduce编程模型;并行计算
1 概述
近年来,智能交通系统(Intelligent Transport System,ITS)蓬勃发展,交通控制和实时交通流诱导成为智能交通系统研究的热门问题,而实现交通控制与诱导的关键问题是实时准确的短时交通流量预测[1]。由于交通流的非线性和不确定性,因此基于数学模型的方法难以处理该问题[2]。而非参数回归方法由于精度高、鲁棒性好的优点已成为交通流短时预测中最重要的方法之一[3-4]。但非参数回归方法的一些问题限制了它在短时交通流预测的实际应用。
非参数回归预测是一种类似于基于案例的推理方法,它不对数据做任何严格的假设,而是在历史数据中搜索与当前状态最相似的集合,并用它们来估算系统未来的状态[5]。非参数回归预测常用的算法是K最近邻(K Nearest Neighbors,KNN)算法。如果历史数据过于庞大,则K最近邻搜索的开销会很大[6]。现有研究大多通过改变历史数据的存储结构来加快搜索速度,如对历史数据进行聚类[7],或使用如动态散列[8]、KD树[9]等数据结构作为数据索引。这些方法都有效地提升了K最近邻搜索的速度,但需要对数据进行一定处理,这对于不断扩充的历史数据库而言开销较大。
非参数回归方法的预测精度直接受限于关键参数的选择。KNN算法中各状态分量的权值和K最近邻数的选取一般采用设定一个取值范围,通过分别进行实际预测以取得最优值的方法[10-11]。但是由于状态向量维数多,权值和K值的取值范围比较大,该方法通常效率较低。针对该问题,文献[5,9]指出可以使用遗传算法来优化参数设置,但遗传算法是一种需要多次迭代的启发式算法,如果模式库较大,则算法需要较长的时间[12]。
本文在现有研究成果的基础上,提出一种海量历史数据条件下的非参数回归短时交通流预测方法。针对海量历史数据条件下的K最近邻搜索问题,使用MapReduce并行计算框架进行K最近邻搜索。针对预测的精确度问题,使用基于MapReduce的遗传算法对关键参数的选取进行优化。
2 MapReduce编程模型
MapReduce是一种分布式可伸缩的编程模型,它运行在分布式文件系统HDFS上,用于大规模数据集的并行运算[13]。MapReduce将分布式计算抽象为Map和Reduce 2个阶段,每个阶段中不同的Map和Reduce过程都是高度并行的。
MapReduce过程首先将源数据划分为若干个数据块,每个数据块的数据被组织成<key,value>形式的键值对,然后由Map过程将输入数据的每条记录分别进行处理,输出一系列键值对,这些键值对按照键进行排序、合并以及分区后,键相同的键值对进入同一个Reduce过程进行处理,并输出最终结果。MapReduce编程模型如图1所示。

图1 MapReduce编程模型
MapReduce对并行运算过程进行了深入的封装,隐藏了容灾、负载均衡等细节,开发者只需关心具体的逻辑。此外,MapReduce具有良好的可伸缩性,能够非常方便地通过增加计算节点的方式提升运算能力,集群中每增加一个计算节点,运算能力得到线性增长。
3 基于MapReduce的短时交通流预测
3.1 历史样本数据
KNN预测算法实际上是一个模式匹配的过程,因此需要从海量的历史数据中提取和建立完备的历史样本库。本文首先以指定的时间间隔筛选出主干道上检测器采集到的交通流量数据;然后对提取出的数据进行平稳化处理,减少随机因素的影响和干扰,消除噪声和误差[11];采用局部最小二乘插值法,并参考文献[14]的实验成果,对采集过程中缺失的部分交通流数据进行补齐和修复。
3.2 参数选择与距离定义
参数选择与距离定义具体如下:
(1)状态分量筛选。影响路段上的交通流量的状态分量很多,如路段上前几个时段的交通流量、上下游路段前几个时段的交通流量等。但并不是所有的状态分量都对当前交通流量有显著影响,可以使用已有文献中提出的相关性分析[7]、主成分分析法[15]等方法筛选出多个比较重要的状态分量。
(2)状态分量权重及K值选择。各状态分量对于交通流状态的影响不同,因此需要赋予不同的权重[16]。KNN算法必须确定一个K值,它对于近邻搜索的速度与预测的精度都有很大影响。本文采用遗传算法对这些值的选取进行优化。
(3)距离定义。距离表征了当前数据与样本数据的匹配程度,本文采用加权的欧式距离:

其中,di为当前数据与样本数据i的距离;λj为第j个状态分量的权重;Xij为样本数据i的第j个状态分量;Yj为当前数据的第j个状态分量。
3.3 Top K算法
KNN算法中要进行从历史数据集中找出与当前点最近的K个点,这个问题可以抽象为从距离值集合A={di|1≤i≤N}中找出K个最小值。如果遍历搜索时间复杂度为O(N2),耗时很大。本文利用一个容量为K的大根堆来解决此问题。大根堆是一个二叉树结构,其中,每个非叶子节点中的值都大于等于它的儿子节点中的值。向大根堆中插入一个元素后需要对堆结构进行调整以保持其性质,调整的时间复杂度为O(logK)。算法描述如下:

大根堆中保存了最小的K个di,而堆顶元素则是这K个值中的最大值,因此后来的每个di只需与堆顶元素比较,若比它更大,则不可能是最小的K个di之一,否则用其替换堆顶元素,得到新的最小的K个di。整个搜索过程的时间复杂度仅为O(NlogK)。
3.4 K最近邻搜索与交通流预测
在海量历史数据条件下利用MapReduce加速K最近邻搜索主要依靠的是MapReduce框架的并行计算机制,使得KNN算法在K最近邻模式匹配时,可以多个部分并行进行,从而缩短了K最近邻的查找时间,其核心部分在于Map和Reduce 2个阶段的设计。基于MapReduce的KNN预测算法流程见图2。
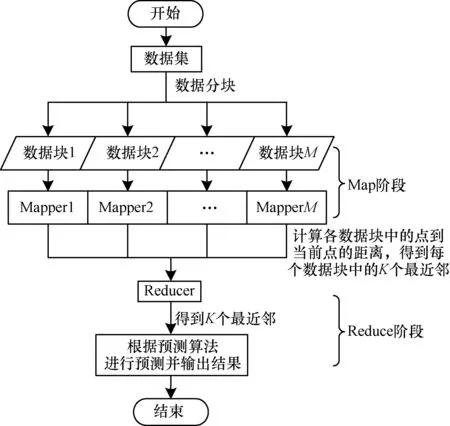
图2 基于MapReduce的KNN预测算法流程
基于MapReduce的KNN预测算法流程具体如下:
(1)Map阶段
Map阶段主要计算当前点与历史数据库中其他点的距离,为下一步的规约提供基础。由于历史数据是海量的,这一阶段比较耗时,可以使用多个Map任务并行处理,每一个Map任务计算出当前点与样本数据点之间的距离,并得到K个最邻近点。
Step1从HDFS上读取历史样本数据,Map Reduce框架会自动将数据划分为若干个块,每一块中的数据都组织成键值对<key,value>的形式,交给一个Mapper过程进行处理。其中,key为数据块的编号;value是该数据块中历史数据的集合,每个元素都是按照3.2节所述方法选取出的若干状态分量构成的状态向量。
Step2Mapper调用Map函数计算value中各个历史数据到当前点的距离,并按照3.3节所述Top K算法,得到每个数据块中的K个最临近点。
Step3输出键值对<key,value>,其中,value是该Mapper过程得到的K个最邻近点信息集合,每个邻近点信息由它与当前点的距离di和该近邻点对应的下一时刻交通流量vi(t+1)构成。
设样本数据集的规模为N,同时启动的Map任务数为M,由于M个Map任务并行运行,因此整个Map阶段的时间复杂度为O(N/M·logK)。
(2)Reduce阶段
Reduce阶段从Map阶段的结果中规约出K个最临近点,并进行交通流的预测。
Step1Reduce节点获得Map阶段产生的键值对<key,value>,将拥有相同key值的value进行规约,构成元组(key:value1,value2,…,valueM),交给Reducer过程处理。
Step2Reducer调用Reduce函数,遍历元组,根据3.3节所述Top K算法得到K个最小距离di以及对应的下一时刻交通流量vi(t+1)。
Step3进行交通流预测,通过对K个最近邻对应的下一时刻的交通流量vi(t+1)进行加权平均,得到预测结果v(t+1)并输出到HDFS中。预测算法的形式如下:

本文对交通流量的预测采用反距离加权法,使得与当前点更近的近邻具有更大的权重,更符合人们的认知[17]。
Reduce阶段需要集中处理 Map阶段产生的M组输出,每组输出中包含K个数据,因此,这一阶段的时间复杂度为O(KM·logK)。
4 基于MapReduce与遗传算法的参数优化
使用遗传算法优化KNN算法中参数的主要开销在于适应度的计算以及进化过程的迭代。本文利用MapReduce的并行计算和批处理的特性,实现遗传算法,加速其参数优化过程。算法流程见图3。
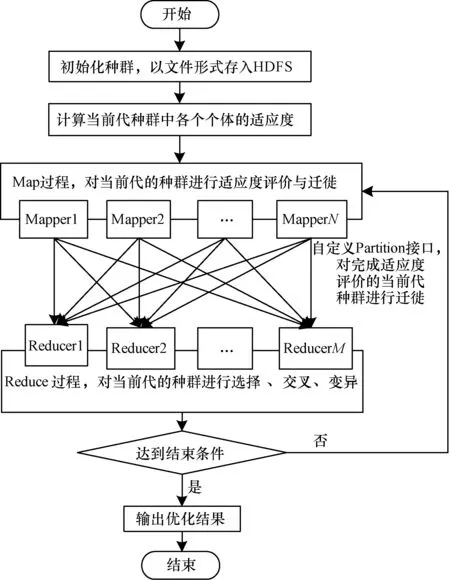
图3 基于MapReduce的遗传算法参数优化流程
基于MapReduce的遗传算法参数优化流程具体如下:
(1)种群初始化。首先使用3.2节提到的主成分分析法选取状态分量,随机为其赋予权值参数,并随机选择一个K值。种群中每个个体都是一组参数的集合,由这些随机选择的参数构成。重复此过程产生一定规模的个体作为初始种群。设种群规模为T,则本阶段时间复杂度为O(T)。
(2)适应度计算。算法关键在于适应度的计算,而衡量某个个体的适应度高低显然是看其对应的K值和各状态分量的参数对于实际交通状况预测的符合程度,计算方法如下:
1)利用历史数据集,提取一部分数据作为历史模式库,选取另一部分作为预测样本库。
2)对于每一个个体,利用其对应的状态分量权值和K值,根据历史模式库对预测样本库中的数据进行离线预测,将预测结果与实际数据对比。定义适应度f为:
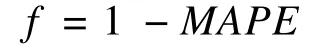
其中,MAPE为平均相对误差:
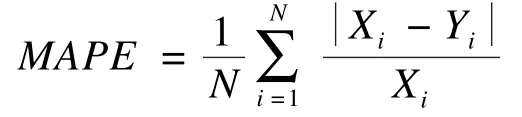
其中,Xi代表第i个周期的实际流量;Yi为第i个周期的预测流量。
适应度计算的主要部分是交通流的预测,比较耗时,因此可以利用 MapReduce来加速。每一个个体的适应度计算是一个如 3.4节所述的MapReduce过程,设历史模式库的规模为H,同时启动的Map任务数为F,则本阶段的时间复杂度为O(T(H/F+KF)logK)。计算好的适应度与参数一起构成一个个体。
3)进化过程。每一代的进化过程可以用一个MapReduce过程来完成,其中,Map阶段进行适应度评价,生成键值对<子种群编号,个体>;Reduce阶段将相同的键对应的值归约起来完成一个子种群的选择、交叉和变异,这样就保持了子种群进化的相对独立性[18]。迁徙可以在Map阶段利用MapReduce提供的Partition接口完成,通过随机改变某个个体的键,将其从原来的子种群迁徙到另一个子种群。设个体中的状态分量数为P,T'为选择过程后的种群规模,同时启动的Map及Reduce任务数分别为N与M,则本阶段时间复杂度为O(T/N+T'P/M)。
4)结束准则。可以在适应度函数收敛和达到一定迭代次数之中选择一种作为结束条件。
上述遗传算法是作为整个预测算法的离线预处理部分,单独运行,不影响实时的交通流预测。只有在遗传算法计算出新的最优参数时,实时交通流预测算法使用的相应参数才需要更新。另一方面, MapReduce的使用加速了遗传算法的运行,因此该算法能满足实际需要。
5 实验结果与分析
5.1 实验环境配置
本文采用开源的Hadoop分布式软件框架搭建MapReduce仿真实验平台,平台构建在局域网中的集群上,由7台机器组成,其中一台为NameNode节点,其余为DataNode节点,相互之间通过100M以太网通信,所有主机采用相同的配置。硬件环境为双核Intel奔腾E6300 2.8 GHz处理器、2 GB DDR3内存、200 GB硬盘;软件环境为Ubuntu 12.04 LTS操作系统、Hadoop 0.20.2、JDK 1.6。
本文算法是基于MapReduce实现的,为了验证其效果,在仿真过程中于单机和Hadoop集群2种不同环境下进行性能测试,其中单机环境下的软硬件环境与Hadoop集群中的机器采用相同的配置。
5.2 MapReduce对K最近邻搜索的加速效果分析
本文对传统的单机 KNN算法与基于 Map Reduce的KNN算法进行K最近邻搜索速度对比实验,以检验MapReduce对K最近邻搜索的加速效果。实验数据为随机生成的海量数据点,其中每个数据点包括5个状态分量,每个分量的值都为0~1之间的实数。数据规模从107~109不等,并对不同规模的数据进行2个算法的搜索速度对比。在测试基于 MapReduce的近邻搜索速度时, Hadoop集群采用4台、5台、6台DataNode机器分别进行实验,以验证算法的伸缩性能。实验结果见图4。
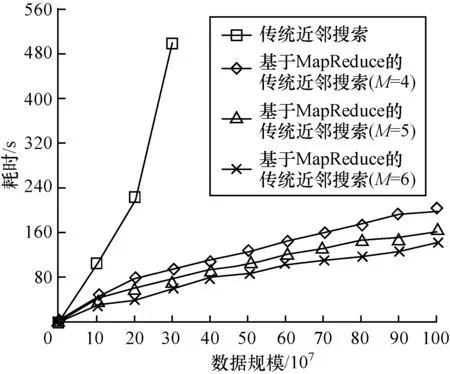
图4 基于MapReduce的KNN算法与传统单机KNN算法的近邻搜索耗时对比
可以看出,基于MapReduce的KNN算法能够有效地提升K最近邻搜索的速度,并且加速效果随着数据规模的扩大愈加明显,而传统的单机KNN算法在数据规模超过一定程度后,受限于单机内存而无法处理。同时,随着DataNode机器数量的增加,基于MapReduce的KNN算法对同样规模数据的搜索速度也在不断提升,表现出了良好的伸缩性能。
5.3 遗传算法优化与加速效果分析
基于MapReduce的遗传算法对参数的优化效果以及对优化过程的加速效果实验使用数据来自美国明尼苏达大学德卢斯分校交通数据研究实验室(The Transportation Data Research Laboratory,http:// www.d.umn.edu/tdrl/traffic/),数据集采自双城高速公路,选取的实验场景位于Interstate 94号公路,如图5所示。路段1为主干公路的上游路段,包括2638号~2641号传感器,路段2为入口匝道,包括2642号传感器,路段3为主干公路的下游路段,包括3176号~3179号传感器。
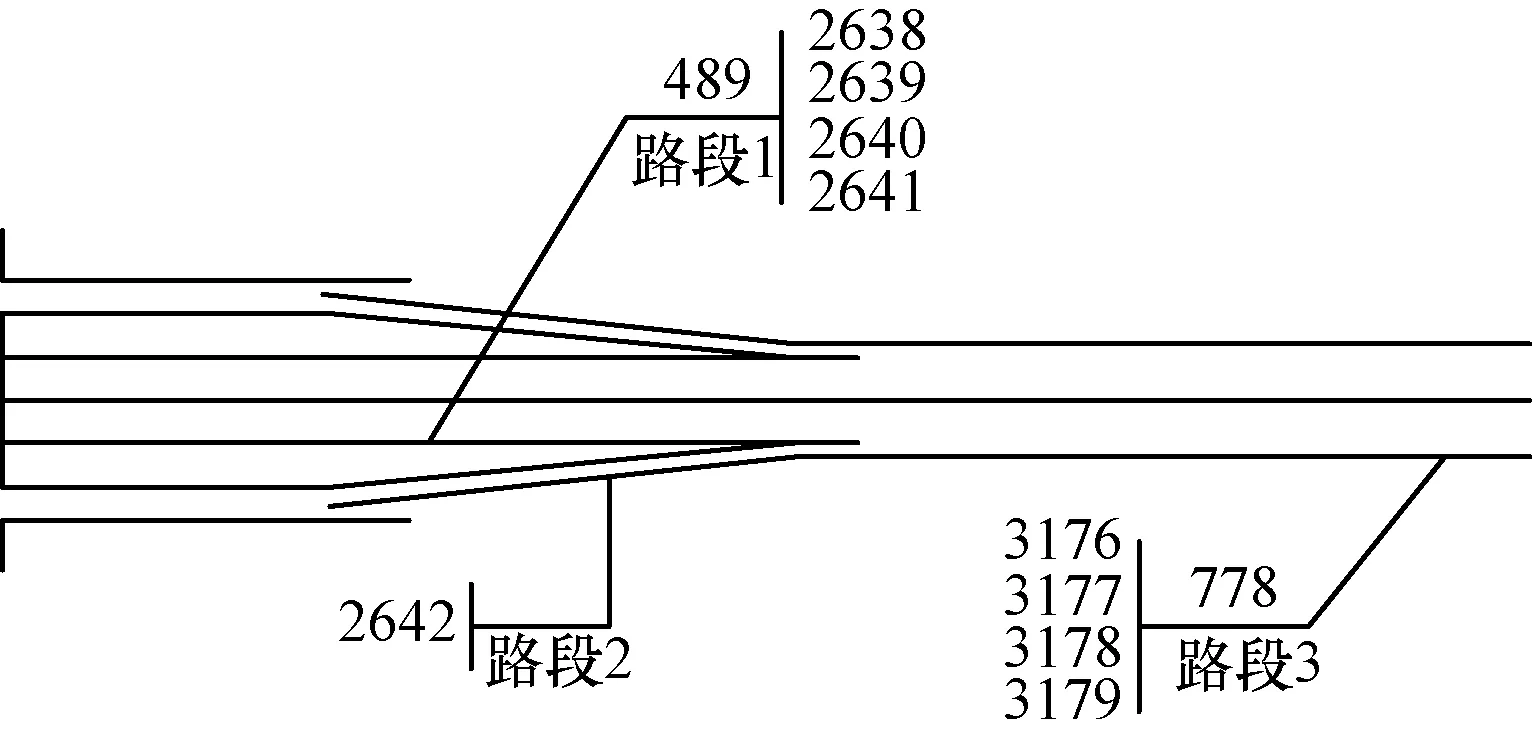
图5 实验道路场景
本次实验选取2013年6月1日-2013年6月30日的数据作为数据集,将路段3上监测点处的流量作为待预测目标。首先使用3.1节中的方法对数据进行预处理,以5 min为预测周期提取数据并补齐缺失数据,处理后的数据大小约为12 MB;然后使用主成分分析方法,得到预测路段3下一时刻流量v3(t+1)需要的状态分量为路段1、路段2、路段3当前时刻的流量,即v1(t),v2(t),v3(t),它们对应的权重参数分别记为λ1,λ2,λ3;接下来使用第4节提出的算法和适应度计算函数对K和λ1,λ2,λ3的值进行优化,得到的最优结果为K=15,λ1=1.67,λ2=0.38,λ3=0.75。
为了验证优化的效果,以K值为例进行对比实验。将λ1,λ2,λ33个参数作为不变量,将K值作为可变量,分别取不同的值进行交通流预测,预测效果的评价以平均绝对百分误差(MAPE)值作为指标。图6显示了K取不同值时预测效果的变化。当K取其他值时,预测的效果变差,这说明基于MapReduce的遗传算法对参数的优化是有效的。
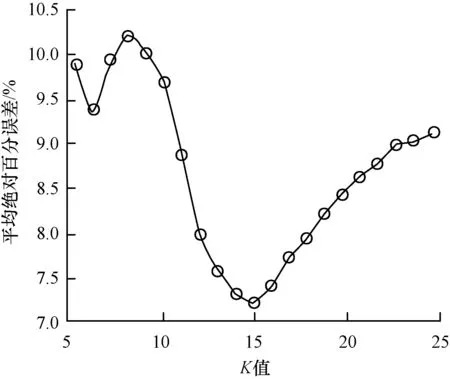
图6 采用不同K值时的预测效果
使用传统的遗传算法对上述场景中K和λ1, λ2,λ3的值进行优化,与基于MapReduce的遗传算法对参数优化的速度进行对比。表1显示了一次迭代进化过程中2个算法的耗时比较。

表1 算法耗时对比 s
5.4 预测效果分析
本节对算法预测效果进行验证和评估。实验采用的场景,K值和其他参数均使用5.3节得到的优化结果,但历史样本数据提取自2011年7月1日-2013年6月30日3年的数据,预处理后的数据大小约为438 MB。使用基于MapRedcue的KNN预测算法对路段3在2013年7月23日一整天共288个预测周期(周期为5 min)的交通流量进行预测,预测流量与实际流量对比见图7。
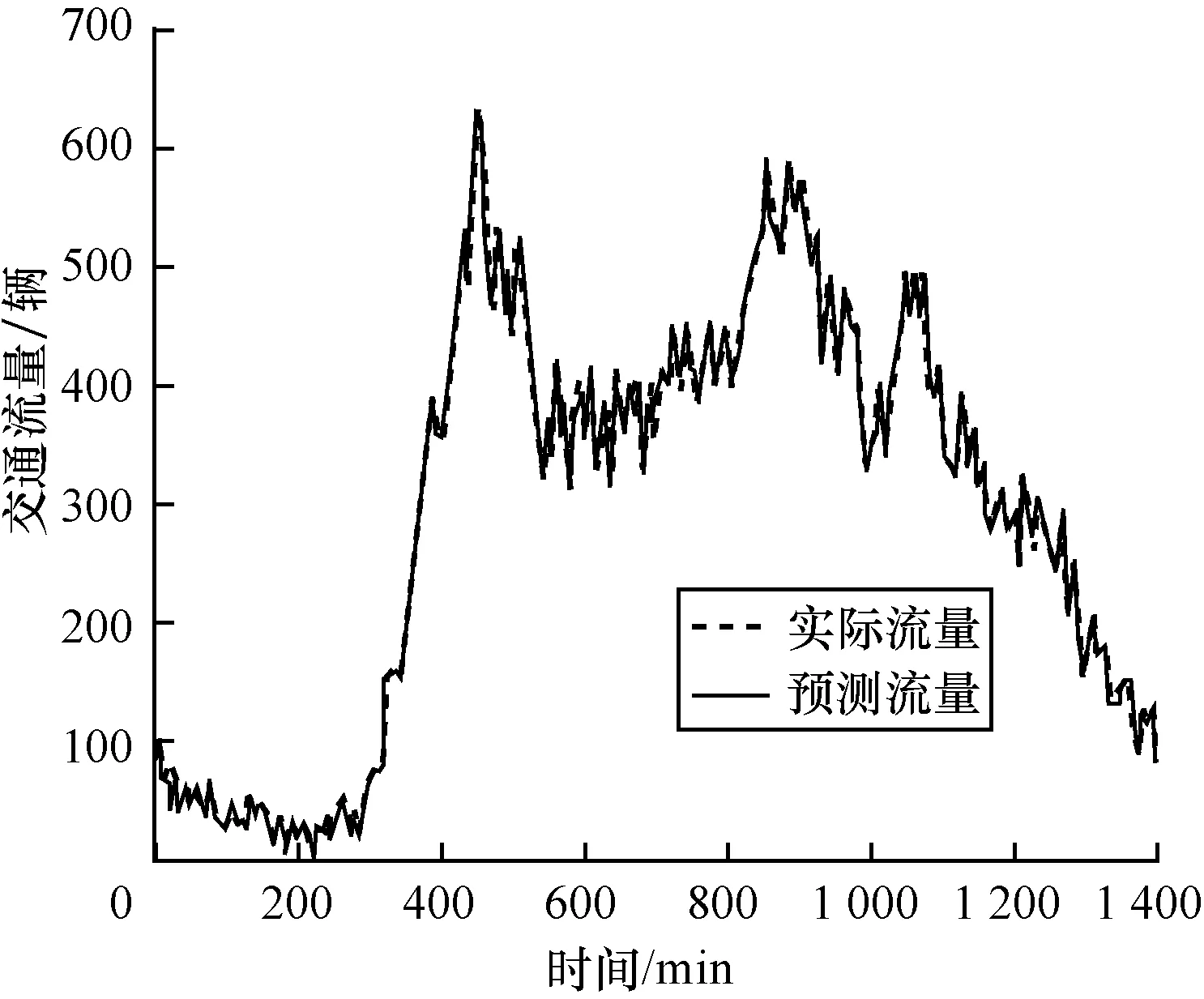
图7 路段3实际交通流量与预测交通流量的对比
采用传统的KNN预测算法与基于MapReduce的KNN预测算法进行综合性能对比。引入平均绝对百分误差(MAPE)和均方误差(MSE)作为预测结果的评价指标。实验结果见表2。
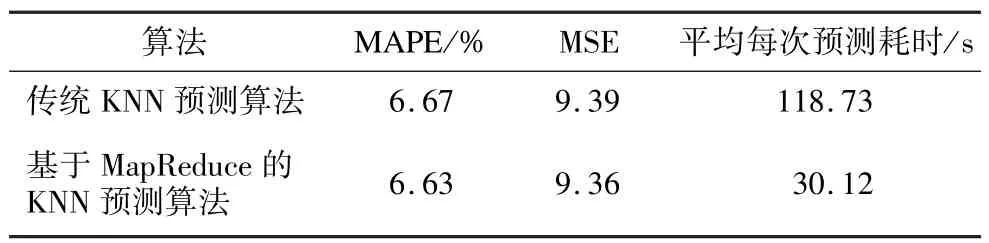
表2 2种预测算法的综合性能对比
可以看出,2个算法均有较高的预测精度。但基于MapReduce的KNN预测算法的预测耗时仅为传统KNN预测算法的1/4左右。这说明本文提出的交通流预测算法在保证一定预测精度的基础上,能够显著提高预测速度。
6 结束语
本文提出一种面向海量历史数据的非参数回归短时交通流预测方法,利用MapReduce将K最近邻搜索过程并行化,并给出MapReduce编程模型下K最近邻搜索与预测算法的流程。实验结果证明K最近邻搜索速度有了明显提高,预测算法可伸缩性良好,并且无需特别的数据结构,历史数据库也能够方便地进行扩充。同时,本文利用基于MapReduce的遗传算法优化KNN算法中的K最近邻数和各个状态分量的参数选取,并通过实验验证了其优化和加速效果。另外,在MapReduce编程模型下,可以通过增加计算节点来应对历史数据的增长,而无需对算法进行大幅修改。这对非参数回归算法应用于实时短时交通流预测具有一定的指导作用。今后将进一步提高算法的预测精度和速度,并将其应用于城市交通流诱导与控制系统中。
[1] Brian L S.Comparison of Parametric and Non-parametric Models for Traffic Flow Forecasting[J].Transportation Research Part C:Emerging Technologies,2002,10(4): 303-321.
[2] 贺国光,李 宇,马寿峰.基于数学模型的短时交通流预测方法探讨[J].系统工程理论与实践,2000, 20(12):51-56.
[3] Davis G,Nihan N.Non-parametric Regression and Shortterm Freeway Traffic Forecasting[J].Journal of Transportation Engineering,1991,117(2):178-188.
[4] Smith B L,Williams B M,Keith O R.Comparison of Parametric and Non-parametric Models for Traffic Flow Forecasting[J].Transportation Research PartC: Emerging Technologies,2002,10(4):303-321.
[5] Oswald R K,Scherer W T,Smith B L.Traffic Flow Forecasting Using Approximate Nearest Neighbor Nonparametric Regression[Z].2000.
[6] Li Shuangshuang.Implementing Short-term Traffic Flow Forecasting Based on Multipoint WPRA with MapReduce[C]//Proceedings of 2012 IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications.Suzhou,China:[s.n.], 2012:287-291.
[7] 宫晓燕,汤淑明.基于非参数回归的短时交通流预测与事件检测综合算法[J].中国公路学报,2003,16(1):82-86.
[8] 张晓利,贺国光,陆化普.基于K-邻域非参数回归短时交通流预测方法[J].系统工程学报,2009,24(2):178-183.
[9] 贾 宁,马寿峰,钟石泉.基于遗传算法优化和KD树的交通流非参数回归预测方法[J].控制与决策, 2012,27(7):991-996.
[10] Huang Zhenjin,Ouyang Hao,Tian Yiming.Short-term Traffic Flow Combined Forecasting Based on Nonparametric Regression [C]//Proceedings of 2011 InternationalConference on Information Technology, Computer Engineering and Management Sciences.[S.l.]: IEEE Press,2011:316-319.
[11] 翁剑成,荣 建,任福田.基于非参数回归的快速路行程速度短期预测算法[J].公路交通科技,2007,3(1):93-97.
[12] Verma A,Llorà X,Goldberg D E,et al.Scaling Genetic Algorithms Using MapReduce[C]//Proceedings of the 9th InternationalConference on IntelligentSystems Design and Applications.Pisa,Italy:IEEE Computer Society,2009:13-18.
[13] Dean J,GhemawatS.MapReduce:Simplified Data Processing on Large Clusters[C]//Proceedings of the 6th Conference on Symposium on Operating Systems Design and Implementation.[S.l.]:USENIX Association,2004: 107-113.
[14] Chang Gang,Ge Tongming.Comparison of Missing Data Imputation Methods for Traffic Flow[C]//Proceedings of 2011 International Conference on Transportation, Mechanical,and Electrical Engineering.[S.l.]:IEEE Press,2011:639-642.
[15] 张晓利,贺国光.基于主成分分析和组合神经网络的短时交通流预测方法[J].系统工程理论与实践, 2007,27(8):167-171.
[16] 于 滨,邬珊华,王明华,等.K近邻短时交通流预测模型[J].交通运输工程学报,2012,12(2):105-111.
[17] 周小鹏,冯 奇,孙立军.基于最近邻法的短时交通流预测[J].同济大学学报:自然科学版,2006,34(11): 1494-1498.
[18] 李 东,潘志松.一种适用于大规模变量的并行遗传算法研究[J].计算机科学,2012,39(7):182-204.
编辑 陆燕菲
A Short-term Traffic Flow Forecasting Method Based on MapReduce
LIANG Ke1,2,TAN Jianjun1,LI Yingyuan3
(1.Guangzhou Institute of Geochemistry,Chinese Academy of Sciences,Guangzhou 510640,China; 2.University of Chinese Academy of Sciences,Beijing 100049,China; 3.CASample Information Technology Co.,Ltd.,Guangzhou 510630,China)
Non-parameter regression method is widely used in short-term traffic flow forecasting,but there is a contradiction on forecasting accuracy and computational efficiency in that method.This paper proposes an improved shortterm traffic flow forecasting method based on MapReduce and genetic algorithm in the context of massive historical data. To improve the search speed of K Nearest Neighbor(KNN),a parallel computing framework MapReduce is used to search the KNN.In data preprocessing stage,genetic algorithm is used to optimize the selection of key parameters,and it accelerates parameter optimization process based on MapReduce to solve the problem of long iterative operation time for genetic algorithm.Experimental results show that the method has high scalability,and it can increase the searching efficiency significantly while the forecasting accuracy is guaranteed.
traffic flow forecasting;non-parametric regression;K Nearest Neighbor(KNN)search;genetic algorithm; MapReduce programming model;parallel computing
1000-3428(2015)01-0174-06
A
TP311
10.3969/j.issn.1000-3428.2015.01.032
广东省中国科学院全面战略合作基金资助项目(2012B091100266);广州市科技计划基金资助项目(2010Y1-C041);广州市科技计划科技支撑基金资助项目(09A11040726)。
梁 轲(1989-),男,硕士研究生,主研方向:智能交通,3S技术及其应用;谭建军,研究员、博士;李英远,硕士。
2014-02-17
2014-03-13 E-mail:liangke723@sina.com
中文引用格式:梁 轲,谭建军,李英远.一种基于MapReduce的短时交通流预测方法[J].计算机工程,2015, 41(1):174-179.
英文引用格式:Liang Ke,Tan Jianjun,Li Yingyuan.A Short-term Traffic Flow Forecasting Method Based on MapReduce[J]. Computer Engineering,2015,41(1):174-179.

