有向双环网络最优路由算法

刘 辉,张 珍,彭慧子,方木云

(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)

有向双环网络最优路由算法

刘 辉,张 珍,彭慧子,方木云

(安徽工业大学计算机科学与技术学院,安徽马鞍山243002)

最优路由的研究对于网络节点的传输具有重要意义,但关于有向双环网络节点的最优路由研究,目前尚无统一的算法。现有有向双环网络的最优路由算法,主要集中在单位步长双环网络及一些特殊双环网络上,对于为数较多的非单位步长有向双环网络最优路由的研究较少。已知有向双环网络的MDD图形为L形瓦,基于L形瓦参数设计提出一种通用的有向双环网络最优路由算法。该算法适用于单位步长和非单位步长有向双环网络。仿真结果表明,与基于[+h]边优先路由及基于二叉树的最优路由算法相比,该算法无需建造竹筏及二叉树的空间,执行效率明显提高。

有向双环网络;路由算法;最优路由;最短路径;L形瓦;对称

1 概述

在光纤通信领域,主干网大多以环型网络的方式提供服务,其中,比较有代表性的有电力通信系统的SDH(Synchronous Digital Hierarchy)环网、电信系统的以太网和有线电视光纤网。近年来,关于环网的研究主要集中在双环网络和多环网络上,其中双环网络(Double-loop Networks,DLN)因其结构相对简单、对称、易扩充且具有一定的容错能力而备受关注[1]。本文通过研究有向双环网络L形瓦构图,提出一种有向双环网络最优路由算法。

2 有向双环网络

有向双环网络分为单位步长网络和非单位步长网络,其图论模型是指这样的有向图G(N;r,S),每个节点记为0,1,…,N-1,从节点i发出2条有向边:i→i+r(modN),i→i+s(modN),其中,r,s为自然数,1≤r≠s＜N,gcd(N,r,s)=1,其图为强连通图,当r=1时,对应的有向图通常记作G(N;1,h),相应的双环网络为有向单位步长双环网络。图1为有向双环网络G(8;2,3)。

图1 有向双环网络G(8;2,3)

双环网络路由的研究包括容错路由[2]、最优路由[3]及其仿真[4-5],目前对于有向双环网络的最优路由方面的研究,主要集中在单位步长双环网络G(N; 1,h)[6-7]及一些特殊的双环网络[8]上。文献[6]提出[+h]边优先的路由算法,并得到一个“竹筏”型空间解;文献[7]提出[+1]边优先的路由算法,文献[8]提出另一类特殊的双环网络G(N;1,h)(h满足某类不等式)的最优路由方法;以上方法各异,但都是针对G(N;1,h),无法推广到非单位步长有向双环网络G(N;r,S)。文献[9]提出非单位步长网络G(N;r,S)的路由算法,但路由方法可以进一步优化。

有向双环网络的 MDD(Minimum Distance Diagram)图形为L形瓦,本文基于L形瓦参数设计有向双环网络的最优路由算法,对单位步长和非单位步长有向双环网络均适用。

根据双环网络的对称性,节点u到节点v的最优路由可以转化为节点0到v-u(如v-u＜0,则转化为N+v-u)的最优路由,因此,研究双环网络的最优路由,只需要考虑0节点到其他节点的最优路由即可。

3 一种有向双环网络最优路由算法

首先在平面直角坐标系的第一象限构造G(N;r,s)有向双环网络MDD图,原点表示0节点,构图方法如下:

定义1第一象限访问节点方法:把Euclid平面上的所有格点排成序列(1,0),(0,1),(2,0), (1,1),(0,2),…,同层按x递减y递增方向访问节点,在每一坐标(x,y)处放置数k∈{0,1,…,N-1},其中,k=xr+ys(modN),如在此之前数k已出现过,则空出此格,考察下一格,直到数0,1,…,N-1都出现为止[10]。

按此方法得到的几何构图是有向双环网络G(N;r,s)对应的L形瓦(L-Shape tile)。如图2所示的L形区域称为具有参数(a,b,m,n)的一个L形瓦,记为N(a,b,m,n),则a=m+p,b=n+q,N=ab-mn,有如下重要性质:

引理1L形瓦参数a,b,m,n,可由下列等式计算[11]:

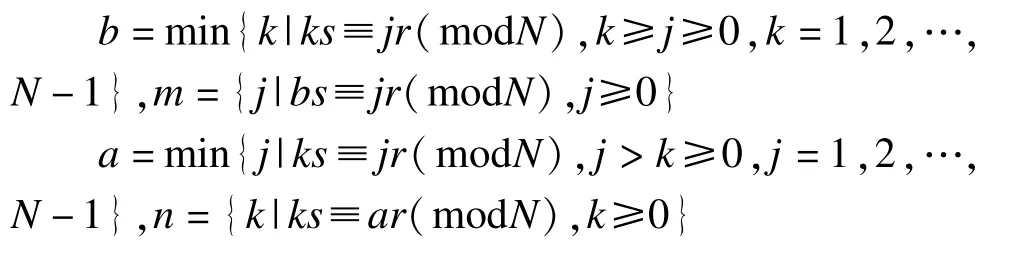
引理2p+qh≡0(modN),-m+bh≡0 (modN),a-nh≡0(modN)[12]。

图2 有向双环网络对应的L型参数

引理3有向双环网络G(N;r,s)中,从节点0出发,无论以什么顺序,经过x条[+r]边和y条[+s]边到节点v的充分必要条件是:v=xr+ys(modN)[9]。

定义2节点0到节点v的最短路径指所有从节点0到节点v的路径中长度最小的路径。即最短路径的长度为x∗+y∗=min{x+y|xr+yh(modN)=v,x≥0,y≥0},x∗和y∗的值可能不惟一[6]。

文献[9]引理2“若x∗+y∗是节点0到节点v的最短路径,则x∗+y∗的值以及x∗和y∗的值都是惟一存在的”。

引理2的证明过程及其结论存在误区。x∗+y∗仅仅是数值,不能将其混为路径,正确表述为“若x∗+y∗是节点0到节点v的最短路径的长度,则x∗+y∗的值是惟一存在的。”但x∗和y∗的值并不惟一,例如:对于双环网络G(39;4,17)节点12而言,其最短路径的长度为3,但x∗=3,y∗=0(此时节点12对应的最短路径3[+r]+0[+s])或x∗=0,y∗=3(此时节点12对应的最短路径0[+r]+3[+s]);类似,对于双环网络G(30;1,7)节点5而言,其最短路径长度为5,但x∗=5、y∗=0或x∗=0,y∗=5,可见x∗和y∗的取值并不惟一。

引理2的证明过程用到双环网络MDD构图作为证明的前提条件,实际上MDD图上只是按照既定的规则生成,保证每个节点仅出现一次,但这不能说明双环网络节点最短路径经过的[+r]边x∗数目及[+s]边y∗数目惟一。

定义3设从节点0到节点v的共有t条最短路径:若,则称为从节点0到节点v的[+r]边最大最短路径。

定理1有向双环网络G(N;r,s)所对应的L形瓦N(a,b,m,n)中,v节点对应坐标为(x∗,y∗),则x×[+r]+y×[+s]为节点0到节点v的[+r]边最大最短路径。

证明:根据定义1的构图规则,v节点对应坐标为(x∗,y∗),则v=x∗r+y∗s(modN)且x∗[+r]+y∗[+s]为节点0到节点v的最短路径。

下面证明x∗[+r]+y∗[+s]为节点0到节点v[+r]边最大最短路径。

用反证法。假设x∗[+r]+y∗[+s]不是节点0到节点v[+r]边最大最短路径,必存在(x′,y′),使得x′[+r]+y′[+s]为节点0到节点v的[+r]边最大最短路径,根据定义 3,x′＞x∗。 因为x∗[+r]+y∗[+s]和x′[+r]+y′[+s]均为节点0到节点v的最短路径,所以x∗+y∗=x′+y′,根据定义1的构图规则,同层按x递减y递增方向访问节点,对于x∗+y∗层节点访问次序为(x∗+y∗,0)…(x′,y′)…(x∗,y∗)…(0,x∗+y∗),在坐标(x′,y′)处已访问节点v,根据定义1构图规则,节点v不可能在(x∗,y∗)处再次访问,与已知v节点在L形瓦对应坐标为(x∗,y∗)矛盾。因此,假设不成立,x∗[+r]+y∗[+s]为节点0到节点v[+r]边最大最短路径。

定理2有向双环网络G(N;r,s)所对应的L形瓦N(a,b,m,n)中,设与v节点对应横轴上的节点为α,与v节点对应纵轴上的节点为β,则节点v为:v=α+β(modN)。

证明:L形瓦N(a,b,m,n)中,β为纵轴上节点,设其坐标为(0,y∗),据引理1,β=y×s(modN);α为横轴上节点,设其坐标为(x∗,0),据引理1,α=x×r(modN)。

则L形瓦N(a,b,m,n)中,v节点坐标为(x∗,y∗),据引理1,有:

v=x×r+y×s(modN)=α+β(modN),证毕。

推论有向双环网络G(N;r,s)所对应的L形瓦N(a,b,m,n)中,如果节点v可表示为:v=α+β (modN),其中,α为横轴上某一节点,其坐标为(x∗, 0);β为纵轴上某一节点,其坐标为(0,y∗),则节点v对应坐标为(x∗,y∗)。

证明过程类似定理1,略去。

在有向双环网络G(N;r,s)所对应的L形瓦N(a,b,m,n)中,已知v节点对应坐标为(x∗,y∗),根据定理1,可知x∗[+r]+y∗[+s]为节点0到节点v的[+r]边最大最短路径;根据定理2及其推论,可快速计算x∗,y∗的数值。这样无需构造双环网络MDD图形,根据其四参数a,b,m,n以及横轴、纵轴上对应节点及节点坐标,就可确定某一预先指定的节点在L形瓦上的坐标,从而得到其[+r]边最大最短路径。下面给出实例说明。

例计算双环网络G(39;7,17)中从节点8到节点2的最短路径。

因为39+2-8=33,求解节点8到节点2的最短路径等价于求解0节点到33的最短路径。对于G(39;7,17)所对应的L形瓦,a=8,b=5,m=1,n=1。可知,L形瓦横轴上节点个数为a-1=7;纵轴上节点个数为b-1=4。

L形瓦横轴上节点存入数组NodeX()={7,14, 21,28,35,3,10},对应坐标分别为(1,0),(2,0),…, (7,0)

L形瓦纵轴上节点存入数组NodeY()={17, 34,12,29},对应坐标分别为(0,1),(0,2),(0,3), (0,4)

对于节点33,逐个与纵轴上节点17,34相减,将差值(或差值+N)和横轴上节点进行比较,一旦相等,则退出,在本例中,33-12=21,而NodeY(3)=21,NodeX(3)=12,因此节点33横坐标为节点14横坐标,纵坐标为节点21对应的纵坐标,即(3,3),故从节点8到节点2的最短路径为3[+r]+3[+s],该最短路径为最大最短路径。

4 路由算法

设源节点为0节点,目的节点为v,下面给出基于L形瓦参数的双环网络的最优路由算法,包括2个部分:

算法1非单位步长双环网络G(N;r,s)最优路由算法

Setp 1初始化参数N,r,s,其中N,r,s为自然数且N≥4,1＜r＜s＜N,且gcd(N,r,s)=1,初始化数组NodeX(),NodeY(),存储横、纵坐标轴上的节点;

Setp 2针对有向双环网络G(N;r,s),按引理1求其L形瓦参数a,b,m,n,计算参数的同时,将横、纵坐标轴上的节点分别存入对应的数组NodeX(),NodeY()中,置初始值i=1,j=1;

Setp 3计算subvalue=v-NodeY(j),如果subvalue＜0,置subvalue=subvalue+N;

Setp 4比较subvalue和NodeX(i),如相等,输出v坐标(i,j),退出;

Setp 5否则置i=i+1,然后返回Step4,直至i＞a-1;

Setp 6置j=j+1,重复Step3～Step5。

该算法需要空间存储节点,存储节点数为a+b-2个,空间复杂度为O(n);算法作有限次比较,比较次数小于(a-1)×(b-1)次,可得v节点在L形瓦上的坐标,继而可得到其[+r]边最大的最短路径。

算法2单位步长双环网络G(N;1,s)最优路由算法。

Setp 1初始化参数N,s,其中,N,s为自然数且N≥4,1＜s＜N,初始化数组NodeX(),存储横坐标轴上的节点;

Setp 2针对有向双环网络G(N;1,s),按引理1求其L形瓦参数a,b,m,n,计算参数的同时,将纵坐标轴上的节点分别存入对应的数组NodeY()中,置初始值i=1,j=1;

Setp 3计算subvalue=v-NodeY(j);如subvalue＜0,跳至Step5;

Setp 4比较subvalue和p,如果subvalue＜p,输出v坐标(subvalue,j),退出;否则比较j和q,如果j＜q,比较subvalue和a,如果subvalue＜a,输出v坐标(subvalue,j),退出;

Setp 5置j=j+1,重复Step3～Step4。

该算法相对于算法1,利用了单位步长双环网络[+1]边的特殊性,单位步长双环网络G(N;1,s) L形瓦图形横轴上节点依次为1,2,…,a-1,算法仅需存储纵轴节点,存储节点数为b-1个,空间复杂度为O(n);算法作有限次比较,比较次数小于b次。

将本文算法和文献[6,9]比较,文献[6]基于[+h]边优先路由,但构造“竹筏”型空间解比较耗费时间;文献[9]中节点路由区域扩充到L形瓦以外,为(a-1)×(b-1)的矩形区域,而本文算法节点路由区域仅限于L形瓦,提高了路由算法的执行效率,编程工具为Visual basic6.0,仿真实验结果如图3所示,本文算法效率上明显优于其他算法。

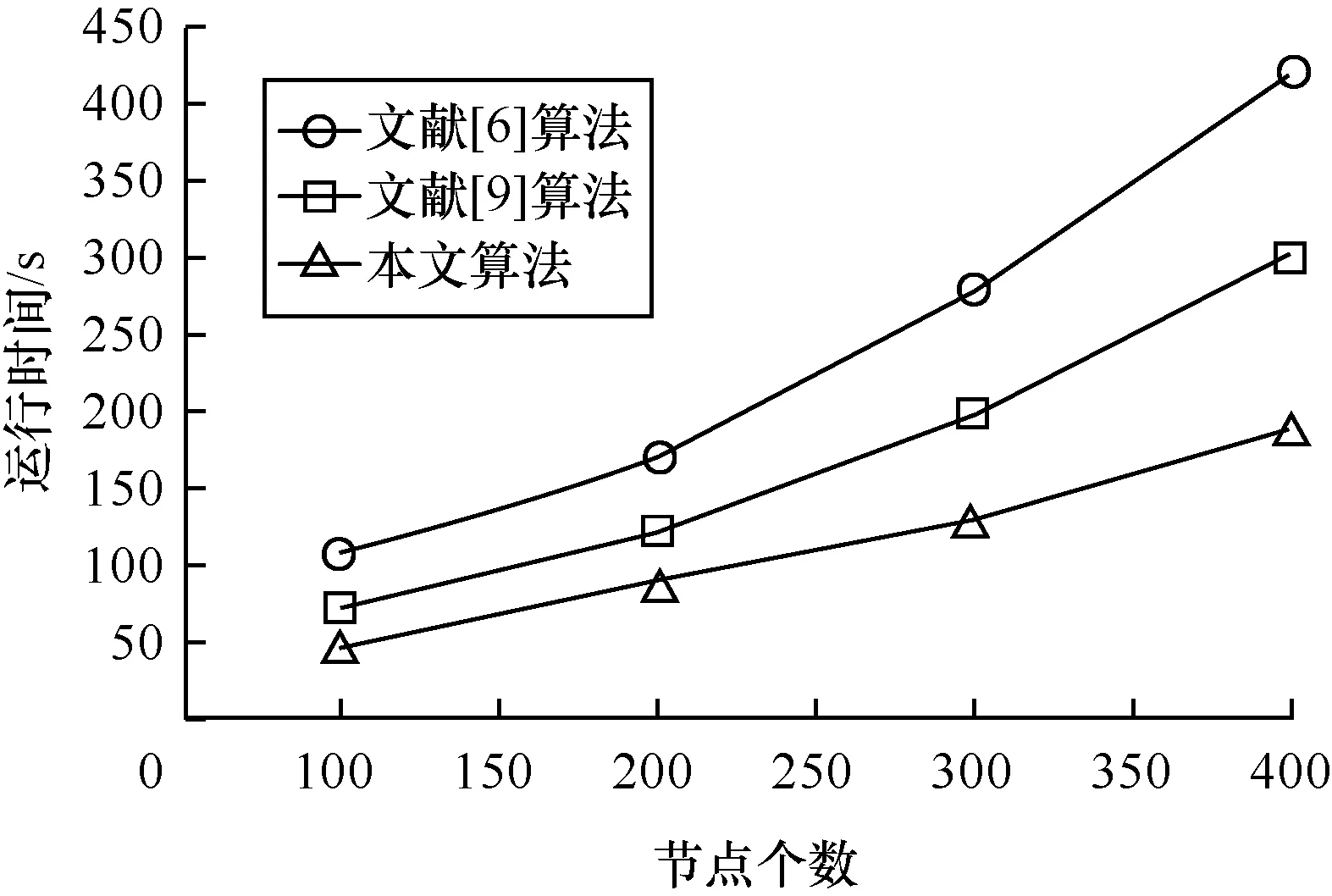
图3 运行时间比较

5 结束语

网络节点路由是网络研究中的一个重要课题,对于有向双环网络节点的最优路由研究,目前尚无明确的统一快捷算法。本文首先通过研究有向双环网络L形瓦构图,在计算有向双环网络L形瓦参数的基础上,提出一种较为通用的最优路由算法,不仅适用于非单位步长有向双环网络,也适用于单位步长有向双环网络,实现了有向双环网络最优路由算法的统一,并针对单位步长有向双环网络的特点进行了算法优化。仿真实验结果表明,本文提出的算法效率上明显优于其他算法,对类似拓扑结构网络节点的最优路由研究有借鉴意义。

[1] 陈业斌,李 颖,郑 啸,等.关于有向环网平均直径的研究[J].通信学报,2013,34(2):138-146.

[2] 方木云,彭慧子,刘 辉.无向双环网络的容错路由研究[J].计算机工程与应用,2013,49(14):105-120.

[3] 刘 辉,方木云,郑 啸.基于L形瓦的无向双环网络直径求解算法[J].华中科技大学学报:自然科学版, 2012,40(9):48-51.

[4] 刘 辉,何本卓,方木云.双优双环网络G(N;1,s)的分布仿真[J].计算机工程,2012,38(8):47-49.

[5] 刘 辉,许发信,方木云.无向双环网络G(N;±r,±s)的图形仿真算法[J].计算机工程,2011,37(6):272-276.

[6] 方木云,屈玉贵,赵保华.双环网络的[+h]边优先寻径策略[J].计算机学报,2008,31(3):536-542.

[7] 陈忠实,靳 蕃.双环网络[+1]边优先最短路径及其寻径策略[J].计算机研究与发展,2001,38(7): 788-792.

[8] 陈协彬.步长有限制的双环网络的最优路由算法[J].计算机学报,2004,27(5):596-603.

[9] 李 颖,陈业斌.有向双环网络G(N;r,s)的寻径策略[J].华中科技大学学报,2009,37(5):45-48.

[10] 刘 辉,方木云.直角坐标系下双环网络G(N;r,s)容错路由研究[J].华中科技大学学报,2010,38(10): 43-46.

[11] 刘焕平,杨义先,杨放春.双环网 G(N;s1,s2)的直径[J].系统工程理论与实践,1999,19(2):58-61.

[12] Dharmasena H P,Yan Xin.An optimal Fault-tolerant Routing Algorithm for Weighted Bidirectional Doubleloop Networks[J].IEEE Transactions on Parallel and Ditributed Systems,2005,16(9):841-852.

编辑 索书志

Optimal Routing Algorithm for Unidirectional Double Loop-network

LIU Hui,ZHANG Zhen,PENG Huizi,FANG Muyun
(School of Computer Science and Technology,Anhui University of Technology,Maanshan 243002,China)

Research on the optimal routing is significant for the transmission between network nodes,and there is no clear unified,efficient algorithms for the research on the optimal routing of Double-loop Network(DLN).Currently, research focuses on the optimal routing of the unit-step and some kind of special DLN,has little work on the non-unit step Unidirectional Double-loop Network(UDLN)which have a greater number.This paper gives general optimal routing algorithm between any two nodes for UDLN on the four parameters of L-shape tile since the Minimum Distance Diagram (MDD)of UDLN is known as L-shape tile,which is suitable for both unit-step and non-unit step UDLN,achieving the unity of optimal routing of directed double-loop network algorithm.Specially,the optimal algorithm for unit-step UDLN is improved based on the general routing algorithm.Compared with[+h]link prior routing algorithm and bintree optimal routing algorithm,the algorithm doesnot need space to build bamboo raft or bintree and efficiency of the algorithm is better than other algorithms.Simulation experiments show the validity of the algorithm.

unidirectional Double-loop Network(DLN);routing algorithm;optimal routing;shortest paths;L-shape tile;symmetry

1000-3428(2015)01-0092-04

A

TP393

10.3969/j.issn.1000-3428.2015.01.017

国家自然科学基金资助项目(61003311);安徽省教育厅基金资助重点项目(KJ2012A262,KJ2013A058)。

刘 辉(1979-),男,副教授,主研方向:数据处理;张 珍、彭慧子,硕士;方木云,教授、博士。

2014-01-09

2014-03-26 E-mail:liuhuiahut@163.com

中文引用格式:刘 辉,张 珍,彭慧子,等.有向双环网络最优路由算法[J].计算机工程,2015,41(1):92-95.

英文引用格式:Liu Hui,Zhang Zhen,Peng Huizi,et al.Optimal Routing Algorithm for Unidirectional Double Loopnetwork[J].Computer Engineering,2015,41(1):92-95.