确定湖泊参照状态过程中频率分析的精度估计

汪靓，华祖林,

1. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室，南京 210098 2. 河海大学水资源高效利用与工程安全国家工程研究中心，南京 210098 3. 河海大学环境学院，南京 210098

确定湖泊参照状态过程中频率分析的精度估计

汪靓1,2,3，华祖林1,2,3,*

1. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室，南京 210098 2. 河海大学水资源高效利用与工程安全国家工程研究中心，南京 210098 3. 河海大学环境学院，南京 210098

确定湖泊参照状态是建立湖泊水质基准的关键步骤之一。以频率分析为基础的方法，如湖泊群体分布法、频率分析法、三分法等广泛地应用于参照状态的研究中；但是，由于湖泊观测数据具有关联性以及难以确定概率分布，这些研究都未给出参照状态估计的置信区间。滑块自助法无需确定观测数据的理论概率分布，同时能很好地克服数据关联性引起的问题，给出这些方法得到的参照状态的置信区间。以太湖为例，分析了确定频率分析过程中，正态分布法和普通自助法的缺陷；结果说明这一方法适合于确定湖泊参照状态的精度。

参照状态；置信区间；滑块自助法；频率分析

为了能够确定湖泊水体水质的状态，保护人们的身体健康不受到污染湖泊水质的影响，促进人类社会和经济的发展，必须建立湖泊的水质基准[1-4]；而确定湖泊水体的参照状态是建立湖泊水体水质基准的基础和重要步骤之一。

湖泊的参照状态是湖泊中营养物及其响应物，如总磷、总氮和叶绿素a等物质的本底值；这一本底值是作为比较湖泊水质状态的参照标准[5-6]。基于对湖泊参照状态的基本认识，从不同的角度出发，各国研究者提出了多种确定湖泊参照状态的方法，其中美国环境保护局(US Environmental Protection Agency, US EPA)[7]提出的参照湖泊法和湖泊群体分布法是确定湖泊参照状态的基本方法；除此以外，其他方法还有：古湖沼学反演法[8-9]、系统动力学法[10-11]、湖泊群体分布法[7,12]、频率分析法[6,12-13]、三分法[14]、广义极值理论法[15]以及土壤指数法[16]等。出于对经济和时间花费上的考虑，统计学方法在其中应用得特别广泛：湖泊群体分布法、频率分析法、三分法、广义极值理论以及土壤指数法等都是统计学方法。统计学方法中尤以理论简单、操作方便的群体分布法、频率分析法和三分法应用更加广泛；而这3种方法的基础都是对总氮、总磷和叶绿素a等物质观测结果的频率分析。

在统计学上，频率分析除了给出分析结果还需要给出结果的精度，也即结果的置信区间[1-2]。在现实中，由于测量误差和随机扰动等偶然性因素的存在，频率分析也必须给出置信区间，以防止偶然因素给估计的结果带来巨大的偏差，这一点在确定湖泊参照状态过程中也不例外；但是，常用的统计学方法只有对独立、正态的观测数据才能够给出正确的置信区间[17]；而湖泊观测数据的来源和性质复杂，不可能满足数据的独立和正态性要求；因此，目前在研究中三分法[14]、湖泊群体分布法[7,12]和频率分析法[6,12-13]等方法均未给出其频率分析结果的置信区间，无法估计其结果的精度；而基于独立、正态假设的统计学方法也无法给出这些方法的频率分析结果的置信区间。

本文在滑块自助法(moving blocks bootstrap)的基础上，给出了一种广泛适用于湖泊群体分布法、频率分析法和三分法等统计学方法中频率分析过程的确定湖泊参照状态置信区间的方法；并以太湖为例，给出了频率分析法下太湖总氮、总磷和叶绿素a参照状态的置信区间。

1 方法(Methods)

1.1 数据类型分析

在确定频率分析的置信区间过程中，对结果影响最大的是数据之间关联性的存在；前人的研究表明，如果将有关联的数据错误地用于独立数据的估计方法，将可能导致分位数估计结果及其置信区间产生50%的误差[18]；因此，有必要考察湖泊参照状态确定过程中，所使用的观测数据之间关联性的特点。表1总结归纳了常见的湖泊群体分布法、频率分析法和三分法进行频率分析时涉及的观测数据的类型和特点。

从表1可以看到，湖泊总氮、总磷和叶绿素a等物质的观测数据类型非常多样，有独立数据、时间序列数据、空间数据以及混合数据等。这些数据中除了湖泊群体分布法多采用独立数据以外，频率分析法和三分法等采用的时间序列和空间数据都肯定具有一定的关联性，而且也很难确定这些观测数据的概率分布；因此，要给出湖泊参照状态中频率分析的置信区间就必须解决概率分布未知和数据之间有关联这2个主要问题。

表1 主要统计方法的数据类型及其特点

1.2 计算方法

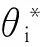
(1)

(2)

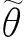
自助法不需要给定观测值的分布就可以计算由观测值确定的任意参数及其置信区间，但是普通的自助法要求数据是独立的；当观测数据有关联时，需要对自助法改进以减弱观测数据之间的关联性；滑块自助法就适合于给出各种关联性数据的置信区间。其主要思想是：在运用自助法前对数据进行滑移分块减弱数据之间的关联进行抽样[18]；具体如下。

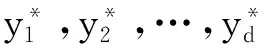
2 数据与处理(Data and processing)

以太湖为例，验证滑块自助法在频率分析为基础的参照状态确定方法中的作用。太湖的观测数据来自文献[19]，文献记录了江苏太湖湖泊生态系统国家野外科学观测研究站(即“太湖站”)中8个站点1991年—2006年共16年的逐月观测数据。考虑到参照状态是受人类活动干扰较少的自然本底浓度，所以本文运用位于太湖湖心区域7号和8号站点的总氮、总磷和叶绿素a的1995年1月—2006年12月144个月完整的观测数据作为研究基础；共288个数据。 考虑到太湖总氮、总磷和叶绿素a浓度受自然气候的影响，天然地存在一个12个月的周期变化；因此，选择分块大小为12。2个观测站的数据分别分块后，每个站点有154个数据块，共308块数据。每次随机抽取100块参与自助法抽样，共抽样1 000次；有文献研究证明，这样的抽样参数足以保证结果的精度。

3 结果与讨论(Results and discussion)

表2给出了太湖7号和8号站点主要统计量的结果。从结果表明这2个站点的总氮、总磷和叶绿素a浓度的概率分布是不均匀的，特别是叶绿素a的浓度容易出现极端高值；偏度的结果表明，7号点和8号点的总氮、总磷和叶绿素a观测值都是偏态分布，而不是对称分布；峰度的结果则表明它们概率分布的峰度远大于正态分布的峰度；这些结果都表明太湖中心总氮、总磷和叶绿素a的浓度的概率分布是复杂的，并不服从正态分布；因此，普通的基于正态分布假设的方法难以给出它们分位数的置信区间，也就无法正确确定太湖总氮、总磷和叶绿素a的参照状态的置信区间。

图1和图2是太湖7、8号2个站点总氮、总磷和叶绿素a观测值前24阶自相关系数图。图中显示的结果清楚表明，虽然7号站点的总磷和叶绿素a观测值没有自相关性；但是，7号站点的总氮和8号站点的总氮、总磷和叶绿素a有非常强的自相关性；因此，普通的自助法是不能给出分位数的正确置信区间的。综合上面的讨论，可以确认，在以频率分析为基础的方法中，一般的统计学方法无法正确地给定太湖参照状态的置信区间。

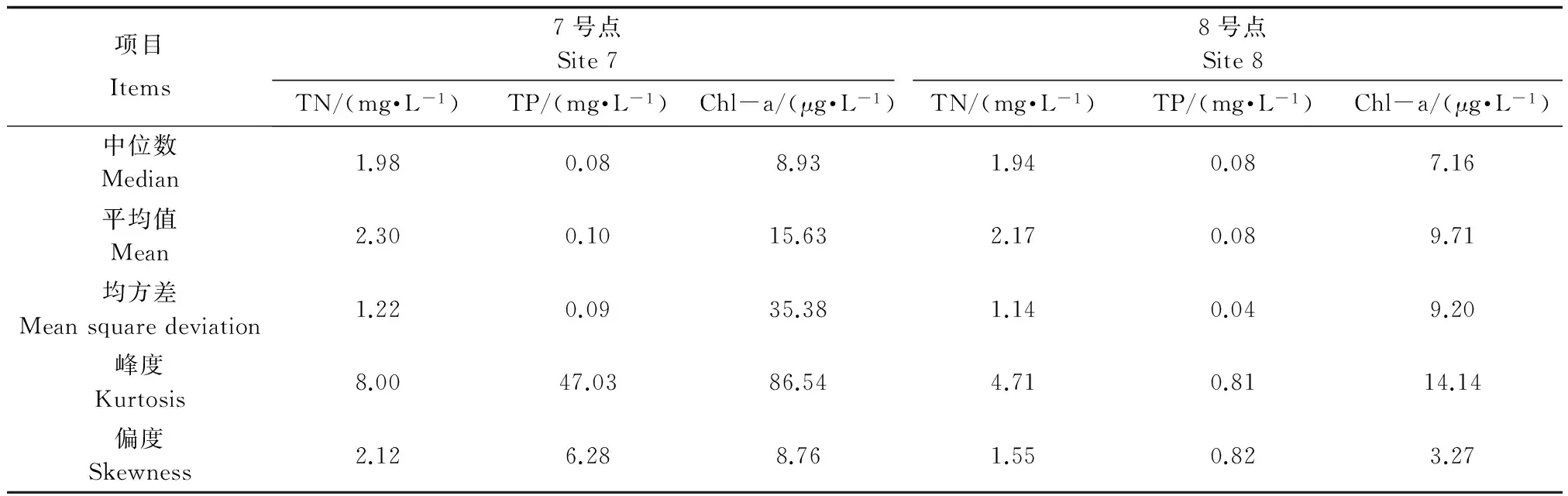
表2 太湖7号和8号站点观测值主要统计量

注：TN、TP、Chl-a表示总氮、总磷和叶绿素a。

Note: TN, TP, Chl-a stand for total nitrogen, total phosphorus and chlorophyll a.

图1 太湖7号站点观测值自相关系数Fig. 1 The autocorrelation coefficients of observations on site 7 in Taihu Lake

图2 太湖8号站点观测值自相关系数Fig. 2 The autocorrelation coefficients of observations on site 8 in Taihu Lake

湖泊群体分布法、频率分析法和三分法都是以湖泊营养物及其响应物浓度的全部或部分观测值为基础；通过统计分析后，以这些观测值某一个分位数的数值作为湖泊的参照状态。常见的分位数有50%[14]、25%[5]以及5%[6,12]。由于本文主要关注太湖参照状态置信区间的计算，即参照状态的精度问题，而与太湖参照状态所对应的具体分位数和数值关系不大；因此，在这方面不加以讨论，只分别对国内外普遍作为参照状态的5%[6,12]和25%[7]分位点的情况进行分析。

表3是不同方法给出的总氮、总磷和叶绿素a的5%分位点及其上下限；其中正态分布法的计算方法是由理论公式给出，具体可见相关文献[20]。

从表3中可以看出，正态分布法、普通自助法和滑块自助法给出总氮、总磷和叶绿素a的5%分位点和置信区间的结果各不相同。其中，正态分布法给出的无论是分位点的估计值还是95%置信区间的结果都与其他2种方法区别很大，而且其总氮、总磷和叶绿素a的估计结果都出现负值，说明这一方法是不合理的；也就是说由于总氮、总磷和叶绿素a的观测值不满足正态分布，湖泊总氮、总磷和叶绿素a的分位点和置信区间不能使用正态分布的方法推断。

普通自助法与滑块自助法给出的分位点结果相同，置信区间也接近；但是，普通自助法给出的总氮、总磷和叶绿素a的结果的置信区间分别比滑块自助法给出的置信区间小15%、20%和13%；这表明，由于普通自助法忽略了观测数据之间的关联性而对置信区间估计错误，严重高估了频率分析结果的精度；所以，其对参照状态的精度估计也肯定是有问题的。以上的分析说明，观测数据的概率分布形式对于确定参照状态的精度影响较大，而数据关联性对于参照状态的置信区间也有一定影响。表4是用普通自助法和滑块自助法估计的25%分位点及其95%置信区间。

表4给出的标准差表明，普通自助法的标准差小于滑块自助法的标准差；也即普通自助法高估了频率分析的精度。进一步比较表3和表4可以发现，普通自助法给出的总氮、总磷和叶绿素a的25%分位点置信区间比滑块自助法给出的结果分别小22%、20%和22%；也就是说，随着频率分析估计的分位点的提高，普通自助法给出的估计精度误差会逐渐增大。因此，若采用三分法这种将观测数据的高分位点作为参照状态的方法，在给出参照状态的估计精度即置信区间时必须采用滑块自助法进行处理；而不能简单地采用正态分布法或是普通的自助法。

表3 不同方法估计的5%分位点及95%置信区间

表4 不同方法估计的25%分位点及95%置信区间

本文通过滑块自助法提出了一种给定湖泊参照状态置信区间的方法。该方法能够广泛地适用于各种类型的观测数据，可以简单而正确地给出以频率分析为基础的湖泊群体分布法、频率分析法和三分法等方法的置信区间。以太湖为例的研究表明使用滑块自助法非常适合于计算得到频率分析的置信区间，进而给出参照状态的精度；正态分布法和普通自助法不适用于参照状态精度的确定。

[1] Feng C L, Wu F C, Zhao X L, et al. Water quality criteria research and progress [J]. Science China: Earth Sciences, 2012, 55(6): 882-891

[2] 孟伟, 吴丰昌. 水质基准的理论与方法学导论[M]. 北京: 科学出版社, 2010: 1-22

[3] 吴丰昌, 孟伟, 宋永会, 等. 中国湖泊水环境基准的研究进展[J]. 环境科学学报, 2008, 28(12): 2385-2393

Wu F C, Meng W, Song Y H, et al. Research progress in lake water quality criteria in China [J]. Acta Scientiae Circumstantiae, 2008, 28(12): 2385-2393 (in Chinese)

[4] 吴丰昌. 水质基准理论与方法学及其案例研究[M]. 北京: 科学出版社, 2012: 1-5

[5] United States Environmental Protection Agency (US EPA). Ambient water quality criteria recommendations: Information supporting the development of state and tribal nutrient criteria, lakes and reservoirs in nutrient ecoregion II (EPA-822-B -00-007) [R]. Washionton DC: Office of Water, Office of Science and Technology, 2000

[6] 郑丙辉, 许秋瑾, 周保华, 等. 水体营养物及其响应指标基准制定过程中建立参照状态的方法——以典型浅水湖泊太湖为例[J]. 湖泊科学, 2009, 21(1): 21-26

Zheng B H, Xu Q J, Zhou B H, et al. Building nutrient and its response indications reference state for criteria enaction: On the case of Lake Taihu, a typical shallow lake in Eastern China [J]. Journal of Lake Sciences, 2009, 21(1): 21-26 (in Chinese)

[7] Gibson G, Carlson R, Simpson J, et al. Nutrient criteria technical guidance manual: Lakes and reservoirs (EPA-822-B00-001) [R]. Washington DC: United States Environmental Protection Agency, 2000

[8] Stockner J G, Benson W W. The succession of diatom assemblages in the recent sediments of Lake Washington [J]. Limnology and Oceanography, 1967, 12(3): 513-522

[9] 李小平, 陈小华, 董旭辉, 等. 淀山湖百年营养演化历史及营养物基准的建立[J]. 环境科学, 2012, 33(10): 3301-3307

Li X P, Chen X H, Dong X H, et al. Nutrient dynamics over the past 100 years and its restoration baseline in Dianshan Lake [J]. Environmental Science, 2012, 33(10): 3301-3307 (in Chinese)

[10] 张礼兵, 霍守亮, 周玉良, 等. 基于系统动力学的湖泊营养物基准参照状态研究[J]. 环境科学学报, 2011, 31(6): 1254-1262

Zhang L, Huo S L, Zhou Y L, et al. Establishing lake reference conditions for nutrient criteria based on system dynamics [J]. Acta Scientiae Circumstantiae, 2011, 31(6): 1254-1262 (in Chinese)

[11] Huo S L, Xi B D, Ma C Z, et al. Stressor-response models: A practical application for the development of lake nutrient criteria in China [J]. Environmental Science & Technology, 2013, 47(21): 11922-11923

[12] 陈奇, 霍守亮, 席北斗, 等. 湖泊营养物参照状态建立方法研究[J]. 生态环境学报, 2010, 19(3): 544-549

Chen Q, Huo S L, Xi B D, et al. Study on establishing lake reference condition for nutrient [J]. Ecology and Environmental Sciences, 2010, 19(3): 544-549 (in Chinese)

[13] 陈奇, 霍守亮, 席北斗, 等. 云贵高原湖区湖库总磷和叶绿素a浓度参照状态研究[J]. 环境工程技术学报, 2012, 2(3): 184-190

Chen Q, Huo S L, Xi B D, et al. Study on total phosphorus and chlorophyll—A reference conditions in Yungui Plateau Ecoregion Lakes and Reservoirs [J]. Journal of Environmental Engineering Technology, 2012, 2(3): 184-190 (in Chinese)

[14] Walter K D, Robert M O. A technique for establishing reference nutrient concentrations across watersheds affected by humans [J]. Limnology and Oceanography: Methods, 2004, 2: 333-341

[15] 华祖林, 汪靓. 一种确定湖泊水质基准状态浓度的新方法[J]. 环境科学, 2013, 34(6): 2134-2138

Hua Z L, Wang L. A New method for estimation the lake quality reference condition [J]. Environmental Science, 2013, 34(6): 2134-2138 (in Chinese)

[16] 顾莉, 李秋兰, 华祖林, 等. 确定太湖流域湖库总磷参照浓度的改进MEI模型[J]. 湖泊科学, 2013, 24(3): 347-351

Gu L, Li Q L, Hua Z L, et al. The improved MEI model for forecasting TP reference condition in Lake Taihu basin [J]. Journal of Lake Sciences, 2013, 25(3): 347-351 (in Chinese)

[17] Song S Q. Environmental and Ecological Statistics with R [M]. Boca Raton: CRC Press, 2009: 49-108

[18] Davison A C, Hinkley D V. Bootstrap Method and Their Application [M]. New York: Cambridge University Press, 1997: 326-378

[19] 秦伯强, 胡春华. 中国生态系统定位观测与研究数据集—湖泊湿地海湾生态系统卷, 江苏太湖站(1991-2006)[M]. 北京: 中国农业出版社, 2010: 239-270

[20] Lversen G R, Gergen M. Statistics: The Conceptual Approach [M]. New York: Springer, 1997: 177-247

◆

Estimation Precision in Frequency Analysis Process for Calculating the Reference Conditions of Lakes

Wang Liang1,2,3, Hua Zulin1,2,3,*

1. Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes of Ministry of Education, Hohai University, Nanjing 210098, China 2. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, China 3. College of Environment, Hohai University, Nanjing 210098, China

4 June 2014 accepted August 2014

Estimation of reference conditions of lakes is one of the key steps for establishing criteria of lakes. The methods based on the frequency analysis, such as lake population distribution approach, frequency analysis approach, and trisection approach, were applied to calculate the reference conditions of lakes. The confidence intervals of reference conditions can not be given due to that the observational data is correlated and it is difficult to determine the probability distribution of the data. The problems caused by data correlations can be overcome by Moving Blocks Bootstrap Method and the confidence intervals could be worked out without any information on the distributions of observational data. As a case of Taihu Lake, the defects of Normal Distribution Way and common Bootstrap method in frequency analysis processes were shown. The results illustrated that the method was suitable for estimating the precision on reference conditions of lakes.

reference conditions; confidence intervals; moving blocks bootstrap; frequency analysis

国家重点基础研究发展计划课题(2008CB418202)；水体污染控制与治理科技重大专项课题(2012ZX07103-005)；国家自然科学基金资助项目(51179052；51379060)；江苏省“青蓝工程”；江苏省高校优势学科建设工程；江苏省普通高校研究生科研创新计划(CXZZ13_0271)

汪靓(1981-)，男，博士，研究方向为水环境模拟与生态水力学，Email: right628@126.com；

*通讯作者(Corresponding author)，E-mail: zulinhua@hhu.edu.cn

10.7524/AJE.1673-5897.20140604001

2014-06-04 录用日期：2014-08-12

1673-5897(2015)1-245-07

X171.5

A

华祖林(1965—)，男，博士，教授，博士生导师，主要研究方向为水环境模拟与污染物输移机制。

汪靓, 华祖林. 确定湖泊参照状态过程中频率分析的精度估计[J]. 生态毒理学报, 2015, 10(1): 245-251

Wang L, Hua Z L. Estimation Precision in frequency analysis process for calculating the reference conditions of lakes [J]. Asian Journal of Ecotoxicology, 2015, 10(1): 245-251 (in Chinese)