基于Backus等效平均的测井资料尺度粗化方法研究

曹丹平

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

基于Backus等效平均的测井资料尺度粗化方法研究

曹丹平

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

三维地震资料具有全面反映地下地质信息的能力,而测井曲线则精确地反映了井点处的储层和岩石物理信息,两者之间在尺度上的差异对地震尺度下的储层预测和流体识别提出了挑战。为了对小尺度的测井曲线进行尺度粗化并探讨其在地震尺度下的岩石物理特征,采用Backus等效平均方法开展了测井资料的尺度粗化方法研究。介绍了基于Backus等效平均的尺度粗化方法；讨论了滑动时窗扫描、参考频率和重采样厚度等关键参数对尺度粗化结果的影响；在此基础上对比分析了测井曲线尺度粗化前、后的岩石物理特征,讨论了不同尺度下岩石物理特征分析结论之间的联系与差异。通过等效平均的方法实现测井曲线的尺度粗化,得到可以与地震尺度相比拟的岩石物理分析结论,对于完善地震尺度下基于井震结合的叠前地震反演与储层预测具有重要意义。

Backus等效平均；尺度粗化；测井尺度；地震尺度；岩石物理特征

测井资料是地震资料分析过程中不可或缺的重要资料,基于测井资料的井震精细标定、岩石物理分析和储层建模等工作奠定了叠前地震反演、储层预测和流体识别的基础。然而,受储层非均质性、测量频率、观测方式等因素的影响,测井资料与地震资料的分辨尺度差异较大,地面三维地震资料横向连续性好但纵向分辨率较低,分辨能力在10m的数量级上,而测井资料纵向分辨率较高,采样间隔一般在0.125m左右,两种地球物理资料在纵向分辨能力上差别达到数十倍以上[1-3]。

通常情况下,通过观测得到的岩石弹性性质取决于相应测量方法的尺度,不同尺度资料之间存在着一定的频散关系[4-5],即对相同地下地质体采用不同的观测尺度进行测量时所得的数值会产生一定的差异。因此,基于测井尺度和地震尺度的测量数据开展岩石物理特征分析也必然会产生不一致的结论。由于反射地震勘探是掌握地下三维空间信息的有效途径,而测井资料则能够精确描述井孔位置处的岩石物理特征,因此讨论小尺度下的测井资料尺度粗化方法,分析不同尺度下的岩石物理特征,对于在地震尺度下开展三维空间范围内的储层预测和流体识别来说具有重要意义。对小尺度测井资料进行整理、块状化、频散校正、尺度粗化等工作能够有效提高井震匹配精度[6-8],并在叠前叠后地震反演、储层预测中发挥着重要作用[9-10]。

尺度粗化实质上是指在地震频带范围内建立测井资料的等效弹性性质,同时确保等效后的地震波传播特征保持不变[11-12]。尺度粗化对于井资料约束的叠前地震反演来说具有非常重要的意义,同样的模型在不同的尺度下正演模拟可以得到不同的地震观测记录；反之,对于给定的地震观测数据来说,也可以由不同尺度的模型来正演模拟得到。此问题一方面是由地震反演问题本身的多解性决定的,另外一方面也与选择的研究尺度有关。对于油藏地球物理资料中常见的岩心、测井、井间地震、VSP/RVSP和三维地震资料来说,多尺度的资料代表了相同地下地质体在相应观测尺度下的不同地球物理响应特征。但是,由于各种资料之间尺度差异较大而不易开展综合研究,通过开展尺度粗化方法研究则有利于分析资料之间在尺度上的联系与差异。因此,针对测井资料开展尺度粗化方法研究,讨论相同物理量在不同尺度下的数值联系与差异,有利于更好地在地震尺度下进行井震关系的匹配分析,同时对多种地球物理资料的综合研究与应用来说也具有重要的意义。

Backus等效平均方法是一种讨论测井曲线尺度粗化特征的有效方法,该方法充分考虑了层状介质在长波长条件下的诱导各向异性特征,在测井曲线尺度粗化等方面发挥着重要的作用[13-14],同时对于各向异性特征最典型的页岩气勘探来说更具有重要的意义。Tiwary等[15]对比分析了简单平均、Backus平均和PCF(pair correlation function)平均3种尺度粗化方法的特点；Sams等[16]深入探讨了Backus尺度粗化方法对原始介质中散射特征的影响；Liner等[17]引入Backus数并讨论了其对各向异性参数的影响。本文从经典的Backus等效平均方法出发,在不考虑各向异性特征的情况下重点探讨针对测井资料的尺度粗化方法及其关键参数的选择,在方法研究的基础上对比分析测井资料尺度粗化前、后的岩石物理特征,以期为今后开展地震尺度下基于井震结合的叠前地震反演和储层预测研究奠定基础。

1 基于Backus等效平均的尺度粗化方法

地球物理探测方法的测量尺度对观测结果的数值具有较大的影响。以速度参数为例,声波测井资料的工作频率为(2～20)kHz,能够探测比较薄的地层；而三维地面地震资料的主频一般为10～100Hz,该频率下地震波的波长远大于薄地层厚度,因此地震频带下测量得到的速度值代表了整段地层在该探测频率下的等效速度。也就是说,当地层弹性参数在测井观测尺度下表现出很强的非均匀性时,为了能够在地震尺度下对介质的整体响应特征进行准确描述,就需要建立该非均匀体在地震尺度下的等效弹性特征。本文讨论测井曲线尺度粗化的目的就是要在地震尺度下建立一个与测井尺度非均匀体性质完全等价的均匀弹性体,确保在该均匀弹性介质中传播的地震波特征与原始介质中传播的地震波特征一致,从而实现在地震尺度下能够通过其等效弹性参数准确合理地描述测井尺度下的非均质储层性质。

为了在不同尺度下保持弹性参数的等价性,尺度粗化方法基本上都采用有效介质理论来近似。对于线性弹性各向同性介质来说,当忽略介质内部由于摩擦和粘滞性引起的能量衰减时可以推导出层状介质有效弹性参数的精确解[11]。Backus等效平均方法描述了薄互层介质在地震尺度下的等效弹性刚度张量,对于各向同性介质来说弹性刚度张量在每一层的方向是相同的,尺度粗化后的等效弹性介质可以表示为

(1)

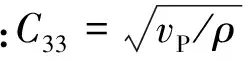
采用公式(1)对小尺度测井资料进行尺度粗化的过程可以表述为:根据测井资料中每层地层的纵、横波速度和密度参数计算得到该层的弹性参数C；在需要开展尺度粗化的位置处选择合适的窗口长度,根据公式(1)计算出在指定深度处的大尺度等效弹性介质参数C*；进一步通过等效介质弹性参数C*计算出该深度位置处尺度粗化后的纵、横波速度和密度等弹性参数。由于弹性参数的加权平均是在指定的窗口范围内开展的,因此窗口长度的选择必然影响着尺度粗化后结果的精度,当加权平均的窗口长度等于或者小于层厚度时,Backus平均所得到的等效弹性参数和原始弹性参数完全相等,即不影响地震波在等效介质中的传播特征。

2 Backus尺度粗化方法中的关键参数

对测井曲线开展尺度粗化的目的在于更好地建立起地震资料和测井资料之间的跨尺度映射关系,其中速度参数是联系测井资料与地震资料的可靠桥梁,也是井震标定中最关键的参数。因此,本文以速度曲线为例来分析测井曲线尺度粗化过程中需要考虑的关键参数。

在采用Backus等效平均方法对声波测井曲线进行尺度粗化时,假设介质成层分布且每层的厚度正好等于测井资料的采样间隔,该间隔通常采用0.125m或0.150m。基于Backus等效平均的尺度粗化方法实质上是一种等效介质理论,测井资料和地震资料之间的尺度差异与指定频率下的地震子波波长直接相关。本文在讨论尺度粗化前、后的特征差异时将研究频率范围考虑在50～500Hz,也就是说当地震波速度为3000m/s时,该频率范围对应的地震波波长范围为6～60m,相对于测井资料的小采样间隔来说此时的地震波波长远远大于测井分层的厚度,从而确保了Backus等效平均方法在开展尺度粗化时的有效性。

2.1 固定时窗与滑动时窗扫描

Backus等效平均所采用的公式(1)表明,尺度粗化方法需要在一定的时窗范围内进行体积平均,对于尺度粗化问题来说时窗长度与该尺度下的地震波波长密切相关。通常情况下地震波速度从浅到深会逐渐增加,因此在不同深度位置处地震波的波长也会发生改变。显然,对不同深度条件下的整条测井曲线都采用相同的时窗长度来开展尺度粗化是不合理的,而采用滑动时窗扫描来处理则是一个很好的选择。所谓滑动时窗扫描就是首先根据测井曲线当前深度处的速度值来计算出一个地震波波长,并根据该波长的长度来确定开展加权平均时时窗的长度,比较简便可行的做法是将该深度位置处的地震波波长设定为时窗长度,并将该时窗的中心点设置在需要开展尺度粗化的位置处。图1为采用滑动时窗扫描开展测井曲线尺度粗化的示意图。

由于测井曲线在不同深度段的速度值并不一样,不同的速度值在给定的参考频率下所对应的地震波波长必然也不一样,因此采用当前深度点的速度值来确定尺度粗化的时窗长度显然更为合理准确。图1中W1时窗内的平均速度为1850m/s,W2时窗内的平均速度为2050m/s,在200Hz参考频率下地震波波长分别为9.25m和10.25m。相对于测井资料0.125m的采样间隔来说,在相距仅30m的范围内W2时窗比W1时窗多采用了7个采样点来进行尺度粗化,此时如果对W1和W2两个窗口采用相同的时窗长度则显然不太合理,这也正是采用滑动时窗扫描来开展测井曲线尺度粗化的优势。基于Backus等效平均的测井曲线尺度粗化方法要求地震波波长远远大于单层的厚度,经验表明两者之间的差别至少应该在10倍以上才能达到较好的效果[2]。因此,在采用滑动时窗扫描时如果给定参考频率下的时窗长度过小,则需要充分考虑该时窗长度是否满足Backus尺度粗化方法的假设条件。

图2为分别采用固定时窗和滑动时窗扫描对实际测井曲线进行尺度粗化后所得结果的对比。由图2可以看到,滑动时窗扫描的结果与固定时窗扫描的结果在大部分区域完全吻合,但是在实际速度与参考速度差别较大的深度位置则产生了一定的偏离。虽然两种时窗扫描结果的速度差异并不算大,但是这种差异也会在一定程度上影响尺度粗化后的测井曲线岩石物理特征。考虑到地震资料与测井资料之间的尺度差异较大,而滑动时窗扫描能够根据指定深度位置处的速度值来开展尺度粗化分析,从而能够更好地满足等效介质理论的基本条件,因此建议在针对实际测井资料开展尺度粗化分析时采用滑动时窗扫描方法。

图2 实际测井曲线尺度粗化时固定时窗与滑动时窗扫描结果对比

2.2 参考频率

在针对测井资料开展尺度粗化时需要充分考虑地震波的波长,在给定速度值的条件下不同的参考频率对应着不同长度的地震波波长。在不同参考频率下开展尺度粗化相当于以该频率下当前深度位置处的地震波波长作为参考,根据该深度下的波长条件来设定滑动时窗的长度并开展尺度粗化分析工作。

图3所示为原始测井曲线与采用滑动时窗扫描方法在不同参考频率下得到的尺度粗化结果对比。图3中的原始测井曲线是在高频条件下测量得到的速度值,由于储层强烈的非均质性导致测井尺度下的速度曲线产生比较剧烈的波动。随着参考频率的降低,地震波波长变大,相应的尺度粗化分析窗口也随之变长,此时尺度粗化对原始曲线的平滑滤波作用也越强,尺度粗化后的曲线也变得越来越光滑。

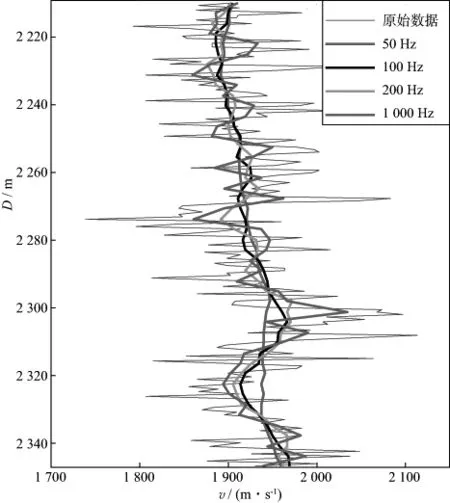
图3 原始测井曲线与不同参考频率下的尺度粗化结果对比

尺度粗化还导致在参考频率下获得的速度值与当前深度位置处的测井曲线原始数值产生差异,并且参考频率越低差异越大,从而导致在该尺度下得到的岩石物理特征分析结论也将相应的发生改变。显然，在50Hz条件下得到的岩石物理分析结论和在2000Hz条件下给出的岩石物理分析结论有差异。因此,直接将原始测井资料中得到的小尺度岩石物理分析结论应用于大尺度下基于地震资料的储层预测是不匹配的,需要对不同参考频率下的尺度粗化结果开展综合对比分析,确定比较合理的参考频率,奠定地震尺度下基于井震结合开展储层预测和流体识别的岩石物理基础。

2.3 重采样厚度

尺度粗化是在指定深度位置处进行,并将以该深度点为中心的滑动时窗范围内的弹性参数体积平均值作为当前深度处尺度粗化后的结果。由于测井采样间隔是等厚度的,为了便于对尺度粗化后的结果开展岩石物理分析,通常也按照等深度间隔的方式来重新抽取尺度粗化后的等效弹性参数数值,当然也可以根据上、下位置处的速度差异等方式来确定尺度粗化后的采样方式。由于在指定位置处的尺度粗化结果与重采样厚度无关,因此减小重采样厚度意味着在比较大的采样厚度点之间进行了加密采样,因此可以在大尺度条件下获取更多的细节特征。也就是说,尺度粗化时选择的重采样厚度参数会影响尺度粗化后测井曲线重采样数值的精细程度,从而导致在大尺度下得到的岩石物理分析结论会出现一定程度的差异,特别是对于很薄的含油气性储层来说,对储层特征反映比较敏感的地球物理参数往往只在很小的深度范围内出现变化,当重采样厚度太大时本来比较敏感的地球物理特征很容易在尺度粗化过程中被平均化,从而导致在地震尺度下很难准确地开展薄层含油气性特征的岩石物理特征分析。以图2为例,当重采样厚度增加一倍时,图中所示重采样后的样点数将减小一半,也就相当于被抽稀了,对于大采样厚度是小采样厚度整倍数的地方来说两者的位置重合,得到的尺度粗化结果也完全一致,因此该参数对测井曲线尺度粗化的影响效果主要表现在对目的层的描述是否足够完整和精细。当然,在大尺度下开展薄层岩石物理特征分析时受参考频率等因素的影响也非常大,因此在地震尺度下分析薄层的地球物理特征需要进行单独的讨论才能有效解决问题。

3 尺度粗化后的测井曲线岩石物理特征分析

Backus等效平均方法中不同参数的选择必然引起尺度粗化前、后的地球物理特征参数发生相应的改变,其中参考频率是尺度粗化过程中最为重要的参数。通过上面的讨论可以看到,随着参考频率的下降,测井曲线中纵向上的剧烈变化特征被平均化,导致尺度粗化后的等效速度曲线变得更为光滑,地层在测井尺度下较强的非均质性通过尺度粗化后得到降低,因此能够更为可靠地反映非均质地层在大尺度条件下的地球物理响应特征。尺度粗化后建立起来的岩石物理分析结论与大尺度下地震勘探所反映的地层特征更为吻合,从而能够有效提高地震尺度下的储层预测和流体识别方法研究与应用的针对性。

图4为尺度粗化前、后纵波速度与横波速度的交会分析结果。由图4可见,尺度粗化前、后纵、横波速度交会的整体趋势没有改变,但是在尺度粗化后的地震尺度下指定深度点处的等效速度发生了改变,从而导致交会结果的细节特征产生很大的差异。由于Backus等效平均方法对薄互层在长波长条件下的地球物理特征参数做了等效处理,并且随着参考频率的降低等效参数的纵向剧烈变化程度变得更为平缓,从而有效降低了该参数所反映的地层纵向非均质性,也可以说尺度粗化方法对原始测井曲线中的参数特征具有平滑滤波作用。图4b的交会结果显然引起对岩性的分辨程度降低,因为受等效平均作用的影响,在测井曲线尺度粗化的同时通过平滑的方式剔除了原始曲线中的局部变化特征,测井尺度下地层在纵向上的强烈非均质特征在大尺度下得到有效降低,尺度粗化后纵、横波速度的数值变化范围被缩小且更为平滑集中。且地震尺度下的纵、横波速度还表现出更为清晰明确的线性拟合关系,这种非常良好的线性拟合关系在测井尺度下是很难准确获取的,更为重要的是这种统计拟合关系对叠前地震反演中纵、横波速度和密度参数的反演来说具有非常重要的意义。

图4表明,相同的物理量在不同的分析尺度下表现出不同的数值范围,因此对原始测井数据在不同尺度下进行粗化后必然引起曲线所对应的岩石物理特征响应发生改变,从而引起岩石物理分析结论产生差异。基于测井资料的岩石物理特征分析结论是通过叠前地震反演来开展储层预测的基础,利用地震反演结果开展储层预测和流体识别显然需要采用与其尺度相匹配的岩石物理分析结果,而直接利用小尺度测井资料得到的岩石物理分析结论将会得到不合理的储层预测结果。从图4可以看出,大尺度下参数交会分析的相对关系保持得非常好,也就是说虽然尺度粗化导致弹性参数数值发生改变,且岩石物理分析结论的细节特征发生变化,但是由于两者之间的线性关系基本不变,且尺度粗化前、后纵、横波速度的主体数值变化范围变化不大,这也正是直接将测井尺度下的岩石物理分析结论应用于地震储层预测和流体识别也能够取得较好效果的根本原因。但是,随着工业界对储层预测定量描述的要求越来越高,地震尺度和测井尺度之间在具体数值方面的差异也引起越来越多的重视,充分采用尺度粗化后的大尺度测井资料有助于得到地震尺度下的岩石物理分析结论,从而有效提高地震尺度下开展储层预测和含油气性识别的定量研究水平。

在此基础上还可以通过测井资料尺度粗化后的结果计算地震尺度下的其它弹性参数，并在该尺度下充分开展相关参数的岩石物理交会分析。图5 为尺度粗化前、后泊松比与μρ的交会分析结果。泊松比、μρ等弹性参数的交会分析对于区分砂泥岩地层岩性来说具有很实际的应用价值,因此在储层预测中经常被采用。显然,图5所示泊松比与μρ在尺度粗化前、后的交会分析结果与前述的结论基本一致。由尺度粗化后(地震尺度下)的交会分析结果(图5b)可以看到,在大尺度下地层的非均质性明显降低,小尺度条件下剧烈变化的测井曲线异常值在尺度粗化过程中被平滑压制,由交会分析结果可以得到两种弹性参数之间更为光滑的线性拟合关系,其对岩性的分辨程度也相应有所降低。

图4 尺度粗化前(a)、后(b)的纵波速度与横波速度交会分析结果

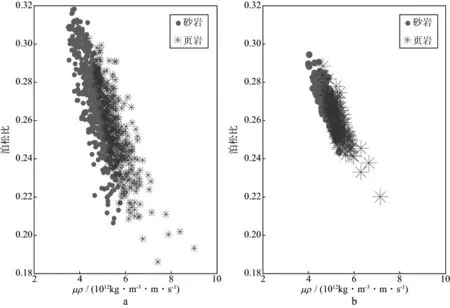
图5 尺度粗化前(a)、后(b)的泊松比与μρ交会分析结果

尺度粗化前、后弹性参数岩石物理交会分析的对比表明,在直接利用地震资料反演结果进行储层预测和流体识别时,需要适当考虑由于观测尺度差异所引起的地球物理参数在数值范围方面的变化和在交会关系等方面的改变,从而在地震尺度下获得更为合理可靠的岩石物理分析结论,以提高地震尺度下储层预测和流体识别的定量描述水平。

4 结论与认识

本文基于Backus等效平均方法开展了测井资料尺度粗化方法研究,讨论了在尺度粗化过程中的几个关键参数。采用滑动时窗扫描方法能够更好地与给定深度位置处的地震尺度特征相吻合；随着参考频率的降低,尺度粗化后弹性参数的数值范围更为平滑集中,弹性参数之间的拟合关系也体现得更为清晰明确；重采样厚度对储层精细特征特别是薄层信息比较敏感,当重采样厚度太大时,测井曲线中本来敏感的地球物理响应特征很容易在尺度粗化过程中被平均化。实际应用效果分析表明,尺度粗化前、后的岩石物理特征分析结论基本一致,受Backus等效方法平滑滤波作用的影响,尺度粗化后的弹性参数数值范围更为集中,大尺度下的岩石物理交会关系变得更为光滑,参数之间的拟合关系也更为可靠。

值得指出的是,由于地层的非均质性导致纵向上剧烈变化的小尺度测井曲线与大尺度地震资料之间存在较大的差异,针对测井资料开展尺度粗化方法研究,不仅有利于更好地在地震尺度下进行井震关系的匹配分析,为地震储层预测向定量描述发展奠定基础,同时对多种地球物理资料的综合研究与应用也具有重要的意义。

[1] 王喜双,甘利灯,易维启,等.油藏地球物理技术进展[J].石油地球物理勘探,2006,41(5):606-613 Wang X S,Gan L D,Yi W Q,et al.Technical progress of reservoir geophysics[J].Oil Geophysical Prospecting,2006,41(5):606-613

[2] 葛瑞·马沃可,塔潘·木克基,杰克·德沃金.岩石物理手册:孔隙介质中地震分析工具[M].徐海滨,戴建春,译.合肥:中国科技大学出版社,2008:45-180 Mavko G,Mukerji T,Dvorikin J.The rock physics handbook:tools for seismic analysis in porous media[M].Xu H B,Dai J C,translators.Hefei:Press of University of Science and Technology of China,2008:45-180

[3] 王延光,韩文功,刘浩杰.多尺度地球物理资料分析与匹配[J].石油地球物理勘探,2008,43(3):333-339 Wang Y G,Han W G,Liu H J.Analysis and match of multi-scaled geophysical data[J].Oil Geophysical Prospecting,2008,43(3):333-339

[4] Winkler K W.Estimates of velocity dispersion between seismic and ultrasonic frequencies[J].Geophysics,1986,51(1):183-189

[5] 郭洪岩,云美厚,艾印双,等.地震资料解释中应用测井数据需注意的几个问题[J].石油物探,2011,50(6):625-629. Guo H Y,Yun M H,Ai Y S,et al.Several problems need to be noticed in the application of logging data to seismic data interpretation[J].Geophysical Prospecting for Petroleum,2011,50(6):625-629

[6] 云美厚,易维启,艾印双.地震与声波测井匹配校正方法研究[J].石油地球物理勘探,2002,37(6):601-605 Yun M H,Yi W Q,Ai Y S.Study on correction methods matching seismic data with sonic logging data[J].Oil Geophysical Prospecting,2002,37(6):601-605

[7] 张广智,刘洪,印兴耀,等.地震解释中声波测井资料的整理方法研究[J].地球物理学进展,2011,26(6):2055-2063 Zhang G Z,Liu H,Yin X Y,et al.Collation method research of acoustic logging data in seismic interpretation[J].Progress in Geophysics,2011,26(6):2055-2063

[8] 隋志强.随井径与岩性变化的声波时差校正方法探讨[J].石油物探,2008,47(2):201-203 Sui Z Q.Research on acoustic moveout correction with variable hole diameter and lithology[J].Geophysical Prospecting for Petroleum,2008,47(2):201-203

[9] 孟恩,徐刚,沈财余,等.约束地震反演中测井数据的标准化及储层的精细标定[J].石油地球物理勘探,2005,40(2):226-232 Meng E,Xu G,Shen C Y,et al.Standard of logging data in constrained seismic in-version and fine labeling of reservoir[J].Geophysical Prospecting for Petroleum,2005,40(2):226-232

[10] 夏吉庄,吕德灵,杨宏伟,等.基于多尺度地球物理资料的流体预测技术[J].石油地球物理勘探,2011,46(2):293-298 Xia J Z,Lv D L,Yang H W,et al.Fluid forecast based on multi-scale geophysical data[J].Oil Geophysical Prospecting,2011,46(2):293-298

[11] Backus G E.Long-wave elastic anisotropy produced by horizontal layering[J].Journal of Geophysics Research,1962,67(11):4427-4440

[12] Gold N,Shapiro S A,Muller T M.An approach to upscaling for seismic waves in statistically isotropic heterogeneous elastic media[J].Geophysics,2000,65(6):1837-1850

[13] Bayuk I O,Ammerman M,Chesnokov E M.Upscaling of elastic properties of anisotropic sedimentary rocks[J].Geophysical Journal International,2008,172(2):842-860

[14] Lindsay R,Koughnet R V.Sequential backus averaging:upscaling well logs to seismic wavelengths[J].The Leading Edge,2011,20(2):188-191

[15] Tiwary D K,Bayuk I O,Vikhorev A A,et al.Comparison of seismic upscaling methods:from sonic to seismic[J].Geophysics,2009,74(2):WA3-WA14

[16] Sams M S,Williamson P R.Backus averaging,scattering and drift[J].Geophysical Prospecting,1994,42(6):541-564

[17] Liner C L,Fei T W.Layer-induced seismic anisotropy from full-wave sonic logs:theory,applocation and validation[J].Geophysics,2006,74(6):D183-D190

(编辑：顾石庆)

The upscaling method of the well logging data based on Backus equivalence average method

Cao Danping

(SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

3D surface seismic data has the advantage of comprehensive exploration for the subsurface geology body relatively,while well logging curves present the reservoir and petrophysical information at the borehole location.It is a big challenge for the reservoir prediction and fluid identification because of the scale difference between surface seismic data and logging data.As to the upscaling of logging curve for petrophysical characteristics research at the seismic scale,the Backus equivalence averaging method is adapted to the upscaling of logging data in this paper.Besides the method of logging curves upscaling based on Backus equivalence averaging,the key parameters of slide sweeping time window,reference frequency and the resample thickness are discussed for the effects of the upscaling method.The petrophysical characteristics from logging curves before and after upscaling are analyzed and compared.The relation and the difference for the raw logging curves and upscaling results have been discussed.The petrophysical analysis conclusions under seismic scale is benefical to the prestack seismic inversion and reservoirs prediction based on the combination of seismic data and logging data.

Backus equivalence averaging,upscaling,logging scale,seismic scale,petrophysical characteristics

2014-03-30;改回日期：2014-07-08。

曹丹平(1978—),男,博士,副教授,主要从事石油地球物理勘探方面的教学与科研工作。

国家重点基础研究发展计划(973计划)(2013CB228604)、国家自然科学基金(41004050)、山东省自然科学基金(ZR2014DM009)和教育部博士点基金(20100133120001)联合资助。

P631

A

1000-1441(2015)01-0105-07

10.3969/j.issn.1000-1441.2015.01.015