弹性多波高斯束逆时偏移方法

毕丽飞,秦 宁,杨晓东,王延光,李向阳

(1.中国石油大学(北京)地球物理与信息工程学院,北京102249;2.中国石油化工股份有限公司胜利油田分公司技术发展处,山东东营257000;3.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022;4.中国石油化工股份有限公司胜利油田分公司石油开发中心,山东东营257000)

弹性多波高斯束逆时偏移方法

毕丽飞1,2,秦 宁3,杨晓东4,王延光3,李向阳1

(1.中国石油大学(北京)地球物理与信息工程学院,北京102249;2.中国石油化工股份有限公司胜利油田分公司技术发展处,山东东营257000;3.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022;4.中国石油化工股份有限公司胜利油田分公司石油开发中心,山东东营257000)

近年来，我国部分老油区勘探开发难度日益增大,勘探目标逐渐转向裂缝油气藏和岩性油气藏等,研究弹性多波理论下的叠前深度偏移算法至关重要。根据高斯束偏移的高效性和逆时偏移的高精度,将弹性多波逆时偏移的实现思想应用于高斯束叠前深度偏移中,研究了一种弹性多波高斯束逆时偏移方法。在射线中心坐标系下,以二维弹性波Kirchhoff-Helmholtz积分为基础,根据多分量地震数据的矢量地震波场传播特征,利用弹性动力学高斯束表征的格林张量推导了弹性波波场正、反向延拓公式和相应的成像公式,并针对转换波的极性反转问题,提出了一种根据入射波入射角的正、负引入符号函数的校正方法。模型和实际资料试算结果验证了该方法的正确性和适用性。

弹性波;高斯束;逆时偏移;正向延拓;反向延拓;极性校正

叠前深度偏移是当前复杂构造地震成像的关键技术。近年来,我国部分老油区勘探开发难度日益增大,勘探目标逐渐转向裂缝油气藏和岩性油气藏等,多地开展了多波多分量地震数据采集。常规多波偏移方法往往将垂直分量当做纵波进行处理,将水平分量当做转换横波进行类似于纵波的处理,整个过程中并没有考虑地震波的弹性矢量波特征,并且其成像效果在很大程度上依赖于波场分离的精度,如果不同波型的能量未完全分离,残余的非本型波能量会在成像结果中产生大量噪声串扰,严重影响成像效果。因此,研究弹性多波理论下的叠前深度偏移算法至关重要。

弹性多波叠前深度偏移算法大致可以分为两大类。一类是基于射线理论的弹性波Kirchhoff偏移。Pao等[1]和Kuo等[2]推导了各向同性介质中弹性矢量波场的Kirchhoff偏移公式并展示了多分量偏移结果,但并没有进行PP波和PS波分别成像;Keho等[3]提出了一种频率域弹性波Kirchhoff偏移方法;Sena等[4]推导了各向异性介质下弹性波Kirchhoff偏移方法;Xue等[5]对X和Z分量进行偏移并得到了PP波和PS波的成像剖面;Duzhinin[6]发展了一种解耦的弹性波Kirchhoff叠前深度偏移方法;Gherasim等[7]实现了三维弹性波Kirchhoff叠前深度偏移算法。另一类是基于波动方程理论的弹性波逆时偏移,以弹性波全波方程为基础,将多波数据的逆时延拓与模型数据的正向延拓波场应用成像条件进行成像,对波动方程的近似少且不受倾角限制。Chang等[8-9]首次将逆时偏移方法应用到多分量地震数据中,此后,Sun等[10]、Biondi等[11]和Yan等[12]将其推广到各向异性介质和三维偏移。此外,近年来很多专家学者也对弹性波逆时偏移做了很多有价值的研究[13-18]。然而,弹性波逆时偏移亦有其局限性:①在偏移过程中不同波型间互相串扰;②逆散射、回转波等引起的低频干扰影响最终成像效果;③虽然成像精度高,但是计算量大,需要极大的空间存储量。而弹性波Kirchhoff积分偏移虽然计算效率高,灵活性强,但是很难对陡倾角、多次波至等问题进行成像。弹性波高斯束偏移是Kirchhoff偏移的改进,它所使用的格林函数是一系列高斯束的叠加,代表了时间和空间局部化且处处正则的地震波场[19],能够对多次波至进行成像且不存在波场的奇异性区域,其成像精度优于Kirchhoff偏移但计算效率相当。

根据高斯束偏移的高效性和逆时偏移的高精度,本文将弹性多波逆时偏移的实现思想应用于高斯束叠前深度偏移中,发展了一种弹性多波高斯束逆时偏移方法。以二维弹性波Kirchhoff-Helmholtz积分为基础,根据多分量地震数据的矢量地震波场传播特征,利用弹性动力学高斯束表征的格林张量推导了弹性波波场反向延拓公式和多波成像公式,并针对转换波的极性反转问题提出了相应的校正方法。最后利用改进的Marmousi2模型和A探区实际多波资料验证了方法的正确性和适用性。

1 弹性多波高斯束逆时偏移方法原理

对于任意射线Ω,建立射线中心坐标系(s,n),其中，s代表Ω上某点到参考点的弧长,n代表Ω附近一点到参考点的距离,坐标系的基矢量分别为同射线Ω相切的单位切向量t和同Ω垂直并指向Ω同一侧的单位法向量n(图1)。

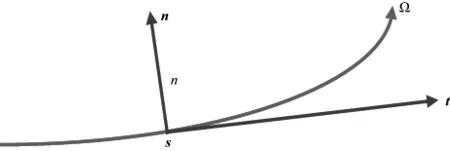
图1 二维射线中心坐标系

根据Babich等[20]和Cerveny等[21]推导的二维抛物线波动方程的解,可得P波和S波高斯束位移公式分别为:

(1)

(2)

式中:uP(s,n,ω,t),uS(s,n,ω,t)和ΨP,ΨS分别为P波和S波位移及加权系数;p和q是动力学射线追踪方程组的解;vP(s)和vS(s)分别为P波和S波速度;ρ(s)为介质密度。

1.1 高斯束反向延拓波场公式

震源点xs引起地下任一点x的位移矢量Um(xs;x;ω)可以通过由震源点试射一系列不同方向的高斯束并筛选对该点有贡献的高斯束进行叠加获取,即：

(3)

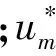
(4)

式中:v*(xs)是震源点的P波或S波速度;ρ(xs)是震源点处的介质密度;ωr表示参考频率;w0为高斯束初始宽度。

Pao等[1]推导了均匀各向同性介质弹性波的Kirchhoff-Helmholtz积分方程[1],忽略体力项之后,可得t0时刻反向延拓的弹性波位移矢量波场:

x,t0)-ui(xr,t)∑im(xr,t;x,t0)]

(5)

式中:ui(xr;t)是由震源xs激发,检波点xr接收到的弹性波地震记录(i=1,2,分别代表水平或垂直记录);S表示包围某区域的闭合面;ti(xr)为xr处应力;Glm(xr,t;x,t0)为格林二重位移张量,表示由xr处l方向单位体力引起的x处位移m方向的分量;∑im(xr,t;x,t0)为格林应力张量。

(6)

式中:Cijkl为应力张量;δ为Kronecker Delta函数;nj表示xr处垂直于积分面指向外法线方向的单位矢量;λ,μ为拉梅弹性系数。

公式(5)中,频率域Glm(x;xr;ω)和∑im(x;xr)为：

(7)

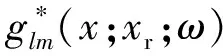
(8)

(9)

其中,格林函数偏导数的高频渐进解为：

(10)

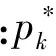
(11)

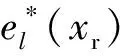
将(4)式、(10)式和(11)式代入(9)式,可得解耦的弹性多波波场延拓公式:

(12)

即反向延拓的P波位移和S波位移分别为:

(14)

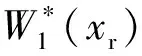
(15)

1.2 高斯束正向延拓波场公式

以纵波震源激发得到的弹性波高斯束表征的正向延拓波场为:

(16)

1.3 极性校正后的成像公式

根据Claerbout反射成像原理,可以利用震源波场与不同波型反向延拓的接收波场之间的零时刻互相关来计算成像值。值得注意的是,由于PS波偏振方向和传播方向不一致,所以在PS波的成像剖面中会出现极性反转的现象。这个问题在逆时偏移中很难解决,而在高斯束逆时偏移方法中通过计算传播角度可以方便解决。PS波传播过程中,入射波具有不同符号的入射角,这使得反射界面处的PS波位移分量相反,最终导致地面接收到的水平X分量地震记录具有相反的极性。根据这个产生机理,可以通过判断入射波入射角的正、负以引入符号函数,直接对PS波成像结果进行极性校正。根据(13)式、(14)式和(16)式,并引入PS波极性校正,可得PP波和PS波成像公式分别为:

(17)

(18)

2 模型与实际资料试算

2.1 Marmousi2模型

为了测试弹性多波高斯束逆时偏移方法对复杂模型的成像能力,利用图2所示改进的Marmousi2模型数据进行试算和分析。将Marmousi2模型抽稀成纵、横向采样点数为701×3401,采样间隔均为5m。正演的多波记录(图3)为中间放炮,共320炮,每炮1401道接收,记录长度为7s,采样间隔0.4ms。由图2可以看出，该模型主要包含浅层三大断层、中部盐丘构造以及深层低速目标区,其PP波和PS波高斯束逆时偏移结果示于图4a和图4b,可见其浅层断层以及中部盐丘构造成像清晰,深层的不整合面及背斜构造也具有较好的成像效果,其精度几乎接近于常规波动方程逆时偏移结果,但其计算效率明显提高。模型试算结果验证了弹性多波高斯束逆时偏移方法的正确性。

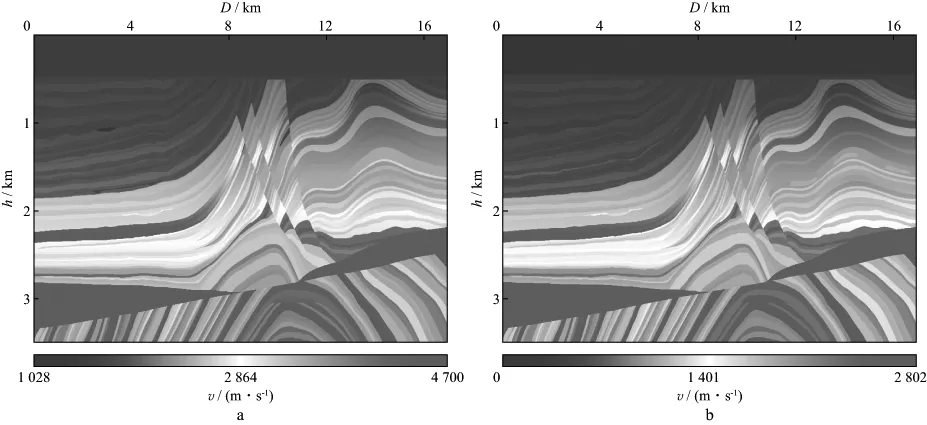
图2 Marmousi2速度模型

图3 Marmousi2模型多分量正演记录

图4 Marmousi2模型弹性多波高斯束逆时偏移结果

2.2 A探区实际资料

以下利用A探区的实际多波多分量数据测试方法的适用性。该数据(图5)的Z和X分量记录长度分别为6s和7s,采样间隔4ms,道间距12m。由图5可以看出，X分量数据信息量少,信噪比很低,Z分量资料品质明显好于X分量。设置密度为常数。

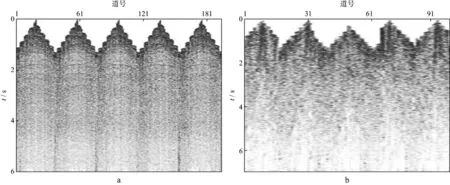
图5 A探区实际多波多分量叠前数据

图6为该探区通过叠前深度层析速度分析获得的P波和S波速度场,利用其进行弹性多波高斯束逆时偏移获得相应的PP波和PS波偏移剖面(图7)。对比图7a和图7b可以看出,PP波和PS波成像结果中主要目的层位(2～3km)深度一致,对应性较好,PS波成像剖面中深层由于速度原因成像效果不理想。此外,PP波成像剖面明显好于PS波成像剖面,究其原因:一是由于原始数据Z分量资料品质好,信噪比高,而X分量数据信息少且信噪比低;二是因为PP波成像仅与P波速度有关,而PS波成像与P波、S波速度均有关系,速度误差对其影响较大。在该实际资料处理过程中,没有经过较多的叠前预处理,若对资料进行精细的配套预处理和速度建模,有望得到更令人满意的高斯波束逆时偏移结果。

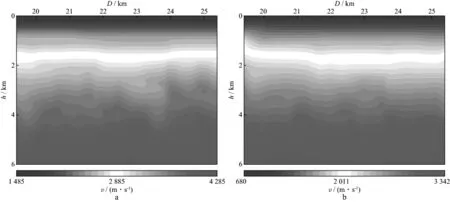
图6 A探区实际资料速度场

图7 A探区实际资料弹性多波高斯束逆时偏移结果

3 结束语

将弹性多波逆时偏移的实现思想应用于高斯束叠前深度偏移中，研究给出了一种弹性多波高斯束逆时偏移方法。针对转换波成像过程中存在的极性反转问题,通过分析其产生机理发展了一种根据反射界面处入射角正、负引入符号函数进行极性校正的方法。Marmousi2模型和A探区实际资料试算结果验证了该方法的准确性和适用性,其优势主要表现在:

1) 该方法中的格林张量是弹性动力学高斯束叠加积分得到的,表示时间和空间局部化且处处正则的弹性波场,能够对多次波至进行成像且不存在波场的奇异性区域,计算效率与弹性波Kirchhoff叠前深度偏移相当;

2) 将弹性波逆时偏移的思路引入到高斯束偏移中,利用正向延拓波场和逆向延拓波场的互相关进行成像,提高了常规弹性波高斯束偏移的计算精度;

3) 分析转换波成像剖面上极性反转产生的机理,结合高斯束本身的优势,通过判断入射波入射角的正、负引入一个符号函数以校正极性,简单有效;

4) 弹性多波高斯束逆时偏移与常规逆时偏移相比,对偏移速度的精度要求低。

[1] Pao Y H,Varatharajulu V.Huygens’principle,radiation conditions and integral formulas for the scattering of elastic waves[J].Journal of the Acoustical Society of America,1976,59(4):1361-1371

[2] Kuo J T,Dai T.Kirchhoff elastic wave migration for the case of noncoincident source and receiver[J].Geophysics,1984,49(5):1223-1238

[3] Keho K H,Wu R S.Elastic Kirchhoff migration for vertical seismic profiles[J].Expanded Abstracts of 57thAnnual Internat SEG Mtg,1987,774-776

[4] Sena A G,Toksoz M N.Kirchhoff migration and velocity analysis for converted and non-converted waves in anisotropic media[J].Geophysics,1993,58(2):265-276

[5] Xue A,McMechan G A.Prestack elastic Kirchhoff migration for multicomponent seismic data in variable velocity media[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000,449-452

[6] Duzhinin A.Decoupled elastic prestack depth migration[J].Journal of Applied Geophysics,2003,54(1):369-389

[7] Gherasim M,Hoelting C,Marfurt K.3-D VSP elastic Kirchhoff pre-stack depth migration-Vinton Dome,Louisiana[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,2649-2652

[8] Chang W F,McMechan G A.Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition[J].Geophysics,1986,51(1):67-84

[9] Chang W F,McMechan G A.3D acoustic prestack reverse time migration[J].Geophysical Prospecting,1990,38(7):737-755

[10] Sun R,McMechan G A.Pres-stack reverse-time migration for elastic waves with application to synthetic offset vertivcal seismic profiles[J].Proceedings of the IEEE,1986,74(3):457-465

[11] Biondi B,Shan G.Prestack imaging of overturned reflections by reverse time migration[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,1284-1287

[12] Yan J,Sava P.Isotropic angle-domain elastic reverse-time migration[J].Geophysics,2008,73(6):229-239

[13] 杜启振,秦童.横向各向同性介质弹性波多分量叠前逆时偏移[J].地球物理学报,2009,52(3):801-807 Du Q Z,Qin T.Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J].Chinese Journal of Geophysics,2009,52(3):801-807

[14] 王娟,李振春,孙小东,等.TTI介质逆时偏移成像[J].石油地球物理勘探,2012,47(4):573-577 Wang J,Li Z C,Sun X D,et al.Reverse time migration in TTI medium[J].Oil Geophysical Prospecting,2012,47(4):573-577

[15] 张智,刘有山,徐涛,等.弹性波逆时偏移中的稳定激发振幅成像条件[J].地球物理学报,2013,56(10):3523-3533 Zhang Z,Liu Y S,Xu T,et al.A stable excitation amplitude imaging condition for reverse time migration in elastic wave equation[J].Chinese Journal of Geophysics,2013,56(10):3523-3533

[16] 陈可洋,陈树民,李来林,等.弹性波联合叠前逆时偏移数值试验[J].石油物探,2014,53(1):8-16 Chen K Y,Chen S M,Li L L,et al.Numerical experiments on the elastic wave united prestack reverse-time migration[J].Geophysical Prospecting for Petroleum,2014,53(1):8-16

[17] 李振春,郭振波,田坤.黏声介质最小平方逆时偏移[J].地球物理学报,2014,57(1):214-228 Li Z C,Guo Z B,Tian K.Least-squares reverse time migration in visco-acoustic medium[J].Chinese Journal of Geophysics,2014,57(1):214-228

[18] 秦海旭,吴国忱.TTI介质弹性波随机边界逆时偏移的实现[J].石油物探,2014,53(5):570-578 Qin H X,Wu G C.The implementation of elastic reverse time migration in TTI media based on random boundary[J].Geophysical Prospecting for Petroleum,2014,53(5):570-578

[19] 岳玉波.复杂介质高斯束偏移成像方法研究[D].青岛:中国石油大学(华东),2011 Yue Y B.Study on Gaussian beam migration methods in complex medium[D].Qingdao:China University of Petroleum,2011

[20] Babich V M,Kirpichnikova N J.Boundary layer method in diffraction problems[M].Petersburg:Leningrad University Press,1974:1-140

[21] Cerveny V,Popov M M,Psencik I.Computation of wave fields in inhomogeneous media[J].Geophysical Journal of the Royal Astronomical Society,1982,70:109-128

(编辑：顾石庆)

Gauss beam reverse time migration method for elastic multiple wave

Bi Lifei1,2，Qin Ning3，Yang Xiaodong4，Wang Yanguang3,Li Xiangyang1

(1.CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum,Beijing102249,China; 2.TechnologyDevelopmentDepartmentofSinopecShengliOilfield,Dongying257000,China; 3.GeophysicalResearchInstituteofSinopecShengliOilfield,Dongying257022,China; 4.PetroleumDevelopmentCenterofSinopecShengliOilfield,Dongying257000,China)

In recent years,the exploration and development of some old oilfields became more and more difficult,exploration target is gradually turning to fractured reservoirs and lithologic reservoirs,so it is important to study prestack depth migration under the theory of elastic wave.Considering the high-efficiency of Gauss beam migration and high-precision of reverse time migration,a Gauss beam reverse time migration for elastic multiple wave has been proposed by applying the idea of reverse time migration to Gaussian beam prestack depth migration.In ray centered coordinates,according to the propagation characteristics of vector wavefield in multi-component seismic data,we derive the forward and backward extrapolation formula and their corresponding imaging formula of vector wavefield by using Green tensor characterized by elastic dynamics Gauss beam on the basis of 2D Kirchhoff-Helmholtz integral for elastic wave,and propose a correction method through adding the sign function related to the positive and negative of incident angle to solve the polarity reversion of PS-wave.Examples of model and real data verify the correction and applicability of this method.

elastic wave,Gaussian beam,reverses time migration,forward extrapolation,backward extrapolation,polarity correction

2014-05-29;改回日期：2014-08-30。

毕丽飞(1976—),男,博士,高级工程师,从事地震资料处理方法研究及科研项目管理等工作。

秦宁(1985—),女,博士,高级工程师,主要从事叠前深度偏移、速度建模与反演等研究。

国家自然科学基金(41204086)、国家科技重大专项课题(2011ZX05006-002)、中国博士后科学基金(2014M551953)和山东省博士后创新项目(201403020)共同资助。

P631

A

1000-1441(2015)01-0064-07

10.3969/j.issn.1000-1441.2015.01.009