时变谱模拟反褶积方法研究
郭廷超,曹文俊,陶长江,王德营
(1.中国科学院地质与地球物理研究所,北京100029;2.中国石油化工股份有限公司江苏油田分公司物探技术研究院,江苏南京210046;3.中国石油大学(华东)地球科学与技术学院,山东青岛266580)
时变谱模拟反褶积方法研究
郭廷超1,2,曹文俊3,陶长江2,王德营3
(1.中国科学院地质与地球物理研究所,北京100029;2.中国石油化工股份有限公司江苏油田分公司物探技术研究院,江苏南京210046;3.中国石油大学(华东)地球科学与技术学院,山东青岛266580)
随着复杂断块、岩性等隐蔽油气藏勘探的不断深入,保幅型非稳态的提高分辨率地震处理技术受到人们的关注。在传统谱模拟反褶积的基础上,提出了一种基于S变换的时变谱模拟反褶积方法。在S变换域通过最小二乘拟合、低通滤波及多道统计加权来获得适应地震记录非平稳特征的时变子波振幅谱,并在反褶积算子设计时考虑信噪比的影响,进而实现时变谱模拟反褶积处理。模型试算和实际资料处理验证了方法的正确性与有效性。
S变换;时变;谱模拟反褶积;分辨率;能量衰减补偿
随着复杂断块、岩性等隐蔽油气藏勘探的不断深入,人们对地震资料处理技术的要求在不断提高,如要求地震资料处理技术能适应子波的时变特征以及体现岩性变化等。常用的反褶积方法基于Robison提出的平稳褶积模型[1]。但是,地震子波在地下介质的传播过程中,由于受到介质非均匀、非完全弹性等因素的影响,表现出明显的非平稳时变特征,导致常规的反褶积方法难以获得好的处理结果,且保幅性较差。谱模拟反褶积是由Rosa等[2]在Ricker工作的启发下首先提出来的。其后,国内很多专家学者提出了许多改进的方法,但都没有考虑子波的时变特性。
近年来人们在Clarke的非平稳褶积模型[3]基础上提出了多种基于时频分析工具的时变反褶积方法,以适应地震记录的非平稳特征,如Gabor域反褶积[1,4-7]、Curvelet域反褶积[8-9]和小波域反褶积[10-11]等,虽然其实现策略各不相同,但都在一定程度上改善了反褶积的效果。S变换能够提供更加精细的时频谱,有利于采用谱模拟技术在获得的地震记录时频谱中提取时变的子波振幅谱。本文在S变换的基础上,对传统谱模拟反褶积方法进行了扩展,提出一种基于S变换的时变谱模拟反褶积方法,使其在保持谱模拟反褶积方法保幅性优势的同时,更好地适应地震记录时变的特征。通过模型试算和实际资料处理验证了方法的正确性与有效性。
1 时变谱模拟反褶积方法
1.1 S变换
Stockwell等提出了S变换[12-14],信号d(t)的S变换如下所示:
(1)
其中的高斯窗函数w(τ-t,f)的公式为:
(2)
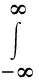
(3)
1.2 时变谱模拟
地震数据表征为d(t,x),对其沿着时间t的方向进行一维S变换,变换后的频谱记为S(τ,f,x),并取绝对值记为|S(τ,f,x)|。下面阐述如何从时变的地震记录振幅谱|S(τ,f,x)|中提取时变子波的振幅谱。
常用的子波振幅谱提取方法,通常基于一定的假设条件,存在一定的局限性。Rosa认为地震子波的振幅谱是平滑的,而反射系数的振幅谱是震荡的,并对地震子波振幅谱进行参数化建模,从地震记录的振幅谱中拟合出子波的振幅谱[2,14-19]。其所用的模型为:
A(f)=fkea0+a1f+…+anfn
(4)
其中:f为频率;k和n为常数。用(4)式对时变的地震记录振幅谱|S(τ,f,x)|沿f方向进行拟合,即:
(5)
其中,A(τ,f,x)是拟合出的时变的子波振幅谱。
通常认为,地震子波在传播过程中的能量衰减由背景衰减和局部异常衰减两部分构成。背景衰减通常指由于地层因素造成的缓慢衰减;局部异常衰减主要指储层中充填油气等流体引起的局部强衰减。为消除子波谱中时间方向上这些局部的能量扰动,避免影响后续的储层预测,并保留宏观的频谱能量衰减变化趋势,对(5)式的时变子波谱A(τ,f,x)沿着时间τ的方向做低通滤波处理,便得到了用于反褶积处理的时变子波谱Af(τ,f,x)。
由于相邻道地震记录的频谱存在一定的差异,因此获取的子波振幅谱在道与道之间也是有差别的,反褶积处理后必然导致连续性变差,为解决这一问题而又不破坏道间频带变化的趋势关系,对子波谱Af(τ,f,x)沿x方向进行多道统计加权处理,处理公式为:
(6)

j=i-n,i-n+1,…,i+n
(7)
综上所述,对地震记录d(t,x)的S谱的绝对值|S(τ,f,x)|,沿f方向进行最小二乘拟合,沿τ方向做低通滤波,最后沿x方向进行多道统计加权处理后,便得到了最终的用于反褶积处理的时变子波谱。
1.3 反褶积算子设计
利用获得的时变子波振幅谱设计反算子。令AMAX(x)=max{Afw(τ,f,x)},且AMAX随偏移距x变化,那么反褶积算子O(τ,f,x)计算公式为:
(8)
其中,斜坡加权系数λ的取值随离开主频的距离增大而减小,其随频率变化的曲线可以是线性或者非线性的曲线,并且0≤λ≤1;ε是白噪系数,可以提高算法的稳定性,其取值不宜过大,一般为0.005≤ε≤0.050,并视资料的信噪比而定;fa,fb,fc,fd是频带展宽控制参数,且满足fa 1.4 时变谱模拟反褶积结果输出 将地震记录的S谱S(τ,f,x)与反算子O(τ,f,x)相乘便可获得提高分辨率后的S谱,由S反变换可知,经下式便可得到提高分辨率后的输出结果: (9) 上述S域的提高分辨率处理,可以看作为S变换域的一个纯振幅滤波处理。Schimmel等[20]的研究指出:由于S变换的频谱在时空域中具有一定局部支撑,在S变换域进行滤波处理时会产生一定的滤波噪声。为解决这一问题,Schimmel给出了如下的公式: (10) 通过时变合成地震记录试算和高邮地区实际二维地震资料的试处理,验证本文提出的S变换域时变谱模拟反褶积方法的正确性与有效性,并与传统的谱模拟反褶积方法进行对比。 2.1 模型试算 一般用品质因子Q来描述地层对地震波能量的吸收作用,那么就可以利用震源子波、品质因子Q及反射系数序列按下式生成一个地震子波随传播深度变化的地震记录[1,5]: (11) 式中:w(f)为频域中的震源子波;r(τ)为反射系数序列;α(τ,f)是与Q值有关的时频衰减因子,可以表达为: (12) 我们采用35Hz的Ricker子波作为震源子波与图1a所示的反射系数序列褶积,得到平稳的合成记录如图1b所示。考虑到地层的吸收作用,选取品质因子Q为40,按照(11)式生成时变的地震记录,如图1c所示。对比图1b与图1c可知,随着时间的增加,时变合成记录的振幅衰减明显。 对图1c的时变合成记录分别采用传统的谱模拟反褶积方法和本文方法进行提高分辨率处理,结果分别如图1d和1e所示。对比图1c和图1d可以看出,经过传统的谱模拟反褶积处理后,合成记录的0~0.4s时间段分辨率有所提高,且振幅增强;而合成记录的0.4~1.0s时间段基本没有明显的变化,衰减掉的振幅能量没有得到恢复,分辨率也没有提高。对比图1c和图1e可以看出,经过本文方法反褶积处理后,衰减掉的振幅能量在一定程度上得到恢复,分辨率也得到了提高。 综合对比图1可以看出,传统谱模拟反褶积方法处理后,在振幅衰减较弱的箭头所示区域,波形得到压缩,而且振幅幅度明显增强;在振幅衰减严重的椭圆框区域,反褶积前、后没有明显变化,波形没有得到明显压缩,衰减掉的振幅能量也没有恢复。而本文方法考虑到了记录的时变特性,对非平稳的地震记录处理后,衰减的振幅幅度得到明显恢复,而且分辨率也有所提高。模型试算结果说明了本文方法适合处理具有非平稳时变特征的地震记录,验证了该方法的正确性。 为进一步分析两种反褶积方法处理前、后合成记录频谱的变化情况,分别对处理前、后的合成记录数据做傅里叶变换和S变换。图2a到图2d分别显示了反褶积处理前、后合成记录的振幅谱,其中图2a为无衰减的合成记录(图1b)的振幅谱;图2b 是时频衰减函数α(τ,f)作用后的时变合成记录(图1c)的振幅谱,可以看出各频段的能量都有所衰减;图2c是对衰减后的合成记录做传统的谱模拟反褶积处理后(图1d)的振幅谱,处理后中高频的能量得到抬升,但与2a相比衰减的能量并没有完全恢复;图2d是对衰减后的时变合成记录经过本文方法处理后(图1e)的振幅谱,与2b图相比,本文方法处理后的频带宽度变宽,并且振幅的幅度恢复到无衰减时(图2a)相当的水平上。 图3a到图3d分别显示了反褶积处理前、后合成记录的S谱,图3a是无衰减合成记录(图1b)的S谱;图3b是经衰减函数作用后时变合成记录(图1c) 的S谱,可以看出各频段随着时间的增加而衰减增强,并且频带逐渐变窄,主频也相应地降低;图3c是传统的谱模拟反褶积处理结果(图1d)的S谱,对比图3b和图3c可以看出,处理后浅层的高频能量得到抬升,主频也有所提高,但中深层的能量变化不大,衰减变化趋势没有改善;图3d是本文时变谱模拟反褶积方法处理后(图1e)的S谱,对比处理前、后的浅、中、深层的S谱,可以看出各个时间段上信号的能量都得到了有效的恢复,并且主频提高,频带变宽。 图1 时变合成记录反褶积试算对比分析 图2 合成记录谱模拟反褶积处理前、后的振幅谱 2.2 实际资料处理 高邮地区是在始新世末的吴堡运动基础上发展起来的断陷盆地之一。该地区具有南断北超、南深北浅、南陡北缓的箕状结构,主要发育北东向断裂系统。该地区发育大量的复杂断块、岩性等隐蔽油气藏,地震资料处理难度大,对反褶积等提高分辨率处理提出了较高的要求。 图4a是该地区的一条二维叠后地震剖面(共300道,2ms采样),可以看出该资料中深层的分辨率不高。我们分别采用传统的谱模拟反褶积方法和本文方法进行反褶积提频处理(图4b和图4c)。综合对比处理前、后的地震剖面可以看出,经过两种方法处理后分辨率都得到了提高;两种方法处理结果的对比表明,本文方法处理后同相轴的连续性增强更加明显,反射波组关系也得到了明显改善(如图4中箭头及方框处所示),且浅、中、深层能量一致性得到提高,体现了时变谱模拟反褶积在提高分辨率的同时能够对中深层能量进行有效的补偿。实际地震资料的试处理结果验证了本文方法的有效性。 对比高邮地区实际二维叠后资料谱模拟反褶积处理前、后的振幅谱和S谱,如图5所示。其中图5a到图5c分别为实际叠后资料、传统的谱模拟反褶积方法处理后以及本文方法处理后的振幅谱,从图中可以看出经过两种方法处理后频谱都得到展宽。图6a到图6c分别为实际叠后资料、传统的谱模拟反褶积方法处理后和本文方法处理后的S谱,可以看出两种方法都能拓宽地震记录的频带,且本文方法对浅、中、深层频带幅度的抬升更加合理,深层能量得到明显改善。图中的虚线为主频变化趋势线,可以看出经本文方法处理后,中深层的主频得到提高,而传统谱模拟反褶积方法中深层主频提高不明显。 图3 合成记录谱模拟反褶积处理前、后的S谱 图4 高邮地区实际二维地震资料的谱模拟反褶积处理结果对比 图5 实际二维地震资料谱模拟反褶积处理前、后的振幅谱 图6 实际二维地震资料谱模拟反褶积处理前、后的S谱 本文提出了一种基于S变换的时变谱模拟反褶积方法。该方法在保持传统谱模拟反褶积方法保幅性好的基础上,通过时变子波谱的提取、低通滤波及多道统计加权,充分体现子波在传播过程中的衰减趋势,能够较好地适应地震记录的非稳态时变特性;同时,所设计的时变反褶积算子考虑了信噪比的影响,在提高分辨率的同时不降低资料的信噪比。合成记录试算结果验证了方法的正确性;高邮地区实际二维叠后资料的试处理证实了方法的有效性。经时变谱模拟反褶积处理后的地震资料在分辨率提高的同时能量衰减得到有效补偿,浅、中、深层能量一致性显著增强,剖面上同相轴的连续性和反射波组关系也得到明显改善,更利于后续解释和反演工作的开展。 [1] 高静怀,王玲玲,赵伟.基于反射地震记录变子波模型提高地震分辨率[J].地球物理学报,2009,52(5):1289-1300 Gao J H,Wang L L,Zhao W,Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J].Chinese Journal of Geophysics (in Chinese),2009,52(5):1289-1300 [2] Rosa A L R,Ulrych T J.Processing via spectral modeling[J].Geophysics,1991,56(8):1244-1251 [3] Clarke G K C.Time-varying deconvolution filters[J].Geophysics,1968,33(6):936-944 [4] Montana C A,Margrave G F.Surface-consistent Gabor deconvolution[J].Expanded Abstracts of 76thAnnual Internet SEG Mtg,2006,2812-2816 [5] Margrave G F,Lamoureux M P,Henley D C.Gabor deconvolution:Estimating reflectivity by nonstationary deconvolution of seismic data[J].Geophysics,2011,76(3):W15-W30 [6] Chen Z B,Wang Y H,Chen X H.Gabor deconvolution using regularized smoothing[J].Expanded Abstracts of 82ndAnnual Internet SEG Mtg,2012,1-5 [7] Ferguson R J,Ercoli M,Frigeri A,et al.Gabor deconvolution of nearsurface georadar data of improved fault imaging[J].Expanded Abstracts of 75thEAGE Annual Conference,2013,10-14 [8] 孟大江,王德利,冯飞,等.基于Curvelet变换的稀疏反褶积[J].石油学报,2013,34(1):107-114 Meng D J,Wang D L,Feng F,et al.Sparse deconvolution based on the Curvelet transform[J].Acta Petroleum Sinica,2013,34(1):107-114 [9] Kumar V,Herrmann F J.Deconvolution with curvelet-domain sparsity[J].Expanded Abstracts of 78thAnnual Internet SEG Mtg,2008,1996-2002 [10] Mundim E C,Schots H A,de Araujo J M,et al.WTdecon,a colored deconvolution implemented by wavelet transform[J].The Leading Edge,2006,25(4):298-401 [11] Matos M C,Marfurt K J.Inverse continuous wavelet transform “deconvolution”[J].Expanded Abstracts of 81stAnnual Internet SEG Mtg,2011,1861-1865 [12] Stockwell R G,Mansinha L,Lowe R P.Localization of the complex spectrum:the S transform[J].IEEE Transaction on Signal Processing,1996,44(4):998-1001 [13] Mansinha L,Stockwell R G,Lowe R P.Local S-spectrum analysis of 1-D and 2-D data[J].Physics of the Earth and Planetary Interiors,1997,103(3):329-336 [14] Stockwell R G.A basis for efficient representation of the S-transform[J].Digital Signal Processing,2007,17(1):371-393 [15] 王德营.自适应谱模拟反褶积技术研究[D].青岛:中国石油大学(华东),2011 Wang D Y.The research of adaptive spectral modeling deconvolution[D].Qingdao:China University of Petroleum(East China),2011 [16] 李振春,李栋,王德营,等.信噪比谱约束的自适应谱模拟反褶积方法研究[J].地球物理学进展,2013,28(1):301-309 Li Z C,Li D Wang D Y,et al.Adaptive spectral modeling deconvolution based on the constraint of signal to noise ratio spectrum[J].Progress in Geophysics,2013,28(1):301-309 [17] 孙成禹.谱模拟方法及其在提高地震资料分辨率中的应用[J].石油地球物理勘探,2000,35(1):27-35 Sun C Y.Spectrum modeling method and its application to seismic resolution improvement[J].Oil Geophysical Prospecting,2000,35(1):27-35 [18] 赵波,俞寿朋,聂勋碧,等.谱模拟反褶积方法及其应用[J].石油地球物理勘探,1996,31(1):101-116 Zhao B,Yu S P,Nie X B,et al.Spectral-modeled deconvolution and its application[J].Oil Geophysical Prospecting,1996,31(1):101-116 [19] 唐博文,赵波,吴艳辉,等.一种实现谱模拟反褶积的新途径[J].石油地球物理勘探,2010,45(增刊1):66-70 Tang B W,Zhao B,Wu Y H,et al.A new way to realize spectral modeling deconvolution[J].Oil Geophysical Prospecting,2010,45(S1):66-70 [20] Schimmel M,Gallart J.The inverse S-transform in filters with time-frequency localization[J].IEEE Transactions on Signal Processing,2005,53(11):4417-4422 (编辑:朱文杰) Research on time-varying spectral modeling deconvolution method Guo Tingchao1,2,Cao Wenjun3,Tao Changjiang2,Wang Deying3 (1.InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China;2.GeophysicalTechnologicalInstituteofJiangsuOilfield,SINOPEC,Nanjing210046,China;3.CollegeofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China) With the advance of subtle reservoirs exploration,such as complex fault block reservoir and lithologic hydrocarbon reservoir,amplitude-preserved and non-stationary processing technologies that enhance seismic resolution have been focused.Based on the conventional spectral modeling deconvolution,time-varying spectral modeling deconvolution on S transform is presented.In S transform domain,we obtained the time-varying spectral of wavelet amplitude by the least squares fitting,low-pass filtering and multi-channel statistical weighting,which adapts to non-stationary seismic records.Take the effect of SNR into consideration,we designed deconvolution operator and realized time-varying spectral modeling deconvolution.Model test and the actual seismic data processing proved the correctness and effectiveness of the method. S transform,time-varying,spectral modeling deconvolution,resolution,energy attenuation compensating 2014-03-31;改回日期:2014-08-25。 郭廷超(1971—),男,博士在读,研究方向为地震资料处理方法研究。 中国石油化工股份有限公司江苏油田分公司物探技术研究院项目(31450007-13-ZC0607-0001)和中海油湛江分公司项目(CJ3ZC1024)联合资助。 P631 A 1000-1441(2015)01-0036-07 10.3969/j.issn.1000-1441.2015.01.0052 模型试算和实际资料处理




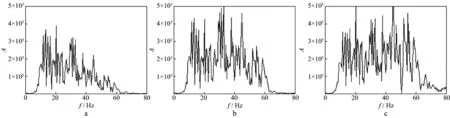

3 结论与认识

