斜拉索耦合振动模型及其参数分析

刘海涛，魏明海，林 坤，肖仪清

1) 哈尔滨工业大学深圳研究生院，深圳 518055；2) 沈阳建筑大学营造与工程管理系，沈阳 110168

【土木与建筑工程 / Architecture and Civil Engineering】

斜拉索耦合振动模型及其参数分析

刘海涛1，魏明海2，林 坤1，肖仪清1

1) 哈尔滨工业大学深圳研究生院，深圳 518055；2) 沈阳建筑大学营造与工程管理系，沈阳 110168

考虑支撑构件对斜拉索参数振动的影响，从整体振动角度研究斜拉索的非线性参数振动特性，提出一个耦合索支撑结构模型.该模型既考虑了斜拉索的几何非线性，也考虑了支撑构件的运动对斜拉索振动的影响. 应用多尺度法对该模型进行摄动分析，得到该模型参数振动时的激励频率及稳定区域边界，讨论模型质量比、刚度比和倾角等参数对幅频响应及稳定性的影响.研究表明，索的非线性参数振动特性并不随质量比和刚度比单调递增，而是存在某一临界值，使索的非线性参数振动特性最大化；随着倾斜角度的增加，索的非线性参数振动特性是单调递增.

结构力学；索支撑结构；斜拉索；耦合模型；幅频响应；参数振动；非线性振动

索支撑结构是工程领域重要的结构系之一，广泛用于世界各地的斜拉桥、桅杆结构和悬索屋盖等工程中．然而，这些索构件很容易由于其支撑构件(如桥面或者屋盖)的小幅振动，而产生具有潜在危害性的大幅振动．在实际工程中，这些拉索与其支撑构件是连接的，但是许多研究都忽略其支撑构件的影响，并使其简化成单个索构件[1-6]．事实上，在索支撑结构中不考虑索的支撑构件对索振动的影响，可能会造成某些严重的错误或者出现某些意想不到的振动．因此，在研究索的参数振动特性中应考虑其支撑构件对其非线性特性的影响．

Tagata[7]研究一个无质量的弦，不考虑垂度的影响，基于量纲一的Mathieu方程确定弦的不稳定区域．Perkins[8]使用一个两自由度的模型，分析拉索由于平方非线性项而引起的面内与面外耦合运动的非线性振动问题．Berlioz等[9]提出一个非线性模型，研究斜拉索在边界激励下的主共振和亚谐波共振时的非线性行为．Wang等[10]使用打靶法和连续的技术，分析斜拉索在支座周期运动激励下的大幅振动和非平面内运动特性．Macdonald等[11]研究索的多个模态发生耦合参数振动时的稳定区域边界问题．Luongo等[12]研究斜拉索在静态风和以正弦方式而运动的下支座同时激励下的非平面内的动力学行为．Caetano等[13-14]通过对某个斜拉桥的物理模型分析以及相关的实验测试，研究索与桥面或者桥塔的动力相互作用，研究结果表明，这种相互作用仅与几个相似于桥面或者桥塔的模态有关，并且这些模态的频率相互接近．Georgakis等[15-16]提出一个交互式的索-桥面耦合模型，研究斜拉索在正弦支座激励以及随机支座激励下的非线性动力响应．Caetano等[17]通过对Guadiana大桥的现场数据实测以及精细的有限元模型分析，研究该桥在环境荷载作用下的索与桥面的相互作用，指出索的大幅振动可能是通过其支座由于桥面振动而引起的运动而激发的．亢战等[18]针对斜拉索参数共振问题建立多自由度数学模型．罗帅等[19]提出适用于桥面运动的斜拉索减振分析理论模型，采用复模态分析方法对拉索-阻尼器系统的模态阻尼特性进行数值分析．周岱等[20]考虑塔柱-拉索-空间结构协同作用，推导拉索在轴向激励作用下的非线性振动方程，研究表明，拉索的振动随着拉索与其支撑结构的频率比不同时，其振动分别可能出现发散，呈现“拍”的特点或者振动的位移幅值接近其初始扰动值．李凤臣等[21]以实际工程拉索为例，采用有限元方法研究水平拉索和斜拉索在端部轴向激励和桥面竖向激励下的参数振动．

现有文献表明，目前对斜拉索参数振动的研究很少考虑其支撑构件的影响．为此，本研究从索支撑结构的整体性出发，考虑索-支撑构件的耦合作用，建立支撑构件与索的参数振动相互耦合振动的模型，着重分析整体结构的各种参数对索非线性参数振动特性的影响．

1 斜拉索参数振动模型

1.1 运动方程

建立图1所示的索支撑耦合结构模型，主要研究斜拉索面内的非线性参数振动特性，假设条件如下：

1)不考虑索的抗弯刚度及抗剪刚度；

2)近似认为索的重力垂度曲线是抛物线；

3)索的轴向伸长用Lagrangian应变来描述；

4)索和梁的变形本构关系服从虎克定律，且各点受力均匀；

5)不考虑梁的扭矩和大变形．

在上述假设条件下，引入如下量纲一参数：

(1)

图1 考虑支撑结构影响的斜拉索振动模型Fig.1 Vibration model of cables considering the supported-structures

其中，ω为索支撑结构平面内的频率；sb为梁在xb方向的位移；sc为索沿yc方向的位移；mb为梁的单位质量；mc为索的单位质量；lb为梁的长度；lc为索的长度；d为索的垂度；Ω为激励荷载的频率；EbIb为梁的抗弯刚度；EcAc为索的抗拉刚度；Eb为梁的弹性模量；Ec为索的弹性模量；H为索的初始张拉力；N为梁的轴向力;ξb和ξc分别为梁和索的阻尼比；pb(xb)为作用在梁上的简弦荷载；βc和βb为无量纲参数.

量纲归一化后的索支撑结构振动方程组和边界条件分别具有如下形式[22]：

(2)

(3)

其中，ρ、χ和θ分别表示索与梁的质量比、刚度比以及倾角．

忽略索轴向变形的影响，索的动应变表达式为

(4)

仅考虑系统的第1阶模态，则梁和索的横向位移量纲一化后的分离变量表达形式为

(5)

其中，q1(t)和q2(t)分别是梁和索的模态幅值；φb(x)和φc(x)分别是梁和索的模态，且有如下表达形式

(6)

其中，Ai(i=1,2,3和4)是梁模态的系数．

把式(6)和式(5)代入式(3)，可得

(7)

对式(7)提取特征方程可得

(-cosβbsinhβb+coshβbsinβbcos2θsinθ)+

(8)

通过数值求解式(8)，可得考虑索支撑结构参数的斜拉索非线性参数振动的第1阶固有频率．

利用Galerkin方法对式(2)进行化简，其一阶模态截断后的两自由度耦合方程为

(9)

其中，ωi、qi、ci、aijk、bijk和f11分别是梁和索的Galerkin系数.

Wei等[22]研究表明，在周期激励幅值较小的情况下，梁无论是发生周期运动还是混沌运动，都具有周期性，且此现象与实验现象[23-25]较为一致．因此，考虑梁的运动具有如下形式：

q1(t)=Qcos(ωbt)

(10)

其中，ωb为梁振动的频率；Q为运动幅值．

把式(10)代入式(9)，整理可得

(c1a1-b1)cos(ωbt)Q+(c1a11-b11)[cos(ω1t)Q]2+(c1a111+b111)[cos(ωbt)Q]3

(11)

与经典的索参数振动模型[9,26]相比较，式(11)不仅考虑索自身的参数对其参数振动行为的影响，同时考虑了其支撑构件对参数振动的影响．

1.2 摄动分析

引入多尺度参数ε，式(11)可变换为

c1a11)[cos(ωbt)Q]2+ε(b111-c1a111)[cos(ωbt)Q]3=0

(12)

设索解的形式为

q2(t,ε)=q20(T0,T1)+εq21(T0,T1)+

O(ε2)+…

(13)

其中，T0=t，T1=εt，且ε≪1;q20和q21分别是不同时间尺度的振幅．

将式(13)代入式(12)，并整理ε的同次幂项的系数可得：

1)ε0阶为

(14)

2) ε1阶为

(c1ξ1-c2)sin(ωbt)ω1Q-(b111-c1a111)cos3(ωbt)Q3-c1a112cos2(ωbt)Q2q20]

(15)

其中,Dn表示第n阶偏微分算子. 从式(14)可求得

q20(T0,T1)=A(T1)exp(iT0ω2)+c.c.

(16)

其中，c.c.表示前面各项的共轭函数．

将式(16)代入式(15)，整理可得

(17)

其中，NST表示非长期项．从式(17)可知索的参数振动有多种发生的可能性，如ω2=3ωb,ω2=2ωb,ω2=ωb,ω2=ωb/2和ω2=ωb/3．

已有文献对索在ωb=2ω2和ωb=ω2激励下的振动行为进行研究[8-9,11,19]，然而很少有文献对索在ωb=ω2/2激励下做过研究．

引入索和参数激励的频率关系：

(18)

其中，σ为调频参数．

把式(18)代入式(17)，消除长期项可得

(19)

设A(T1)的极坐标表达式为

(20)

其中，φ(T1)表示相变角度；B(T1)表示幅值. 分离实部和虚部并整理可得

(21)

其中，Φ(T1)=-φ(T1)+2σT1．

由于在式(11)中存在参数激励项和非线性耦合项，索的振动项有可能在同一个激励幅值或者频率作用下存在多个值，因此，讨论索稳态运动时解的稳定性是有必要的．考虑B(T1)和Φ(T1)有如下的小扰动形式：

(22)

其中，下标1表示稳态响应；下标0表示稳态响应的小扰动解．

把式(22)代入式(21)，并应用Kevorkian等[27]提出的可解条件，可求得特征方程的表达式为

(23)

其中，

(24)

在稳定区域的边界上，式(24)的特征值的实部是零，因此，稳定区域的边界条件为

(25)

2 数值算例分析

由于模型中梁和索的物理参数都对索的非线性振动行为有影响，因此，选取该模型的一组参数作为基本模型，即ρ=0.01，χ=0.02，μ=1 000，ν=0.03和θ=π/3，然后基于这组参数的模型，详细讨论模型中的质量比、刚度比和倾角对索的非线性响应和稳定性的影响．

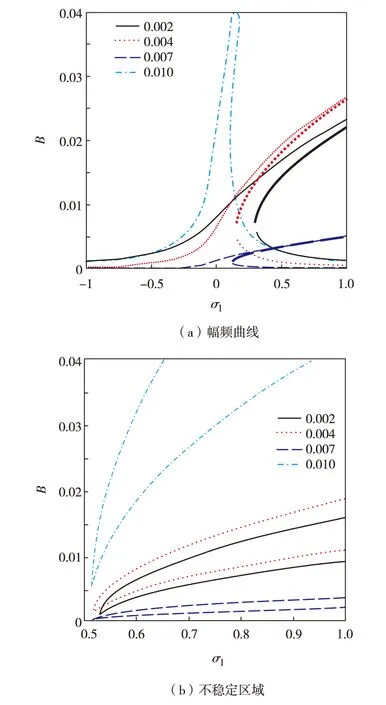
图2 质量比对索的非线性响应的影响Fig.2 (Color online) Effects of mass ratio on the nonlinear response of a cable

图2为耦合模型在参数激励幅值为Q=0.01时，模型中的质量比在1∶2参数共振附近区域对索的非线性行为的影响.由图2(a)可看出，当质量比参数从0.002增到0.004时，频率响应曲线趋向于软化；从0.004增到0.007时，频率响应曲线则趋向于硬化；从0.007增到0.010时，频率响应曲线又趋向于软化.对于索的稳定性区域，模型中的质量比有一个类似的影响，如图2(b)，不同质量比计算出索的稳定性区域的大小从高到低依次为ρ=0.010,ρ=0.004,ρ=0.002和ρ=0.007. 此种现象说明,斜拉索容易在与其支撑构件质量比较大的系统中发生参数振动现象.

图3 刚度比对索的非线性响应的影响Fig.3 (Color online) Effects of stiffness ratio on the nonlinear response of a cable

图3为耦合模型在参数激励幅值为Q=0.01时，模型中的刚度比在1∶2参数共振附近区域对索的非线性响应和稳定性的影响.从图3(a)可知，当刚度比小于0.020时，频率响应曲线总是趋向于软化，但是，当刚度比超过0.020时，频率响应曲线则趋向于硬化.由图3(b)可知，当刚度比较小时，如χ=0.002， 索在参数激励作用下易在较大的扰动频率范围内变得不稳定.索的不稳定区域由不同刚度比计算出来的值从大到小依次为χ=0.020,χ=0.010,χ=0.002和χ=0.200. 这种现象表明，对于索支撑结构中的索构件，存在一个合适的刚度比容易引起其参数振动.

图4 倾角对索的非线性响应的影响Fig.4 (Color online) Effects of the varying angle on the nonlinear response of a cable

图4给出耦合模型中索的倾斜角度变化对其非线性响应和稳定性的影响. 不同于前2个参数的影响， 索的频率响应曲线和稳定区域随着倾斜角度的增大而增加， 如图4. 但是，当倾斜角从π/6增到π/5时，频率响应曲线和稳定区域没有明显变化.

3 结 论

本研究提出一个考虑耦合作用的索-梁振动分析模型，并利用该模型研究索的非线性参数振动特性.模型中不仅考虑梁对索的影响，还考虑索的几何非线性影响.研究表明：

1) 由于索与其支撑结构耦合的影响，索可能发生多种参数共振形式，如ω1=3ω2、ω1=2ω2、ω1=ω2、ω1=ω2/2和ω1=ω2/3.

2) 索的频率响应曲线总是表现出硬化特征，对于模型中的质量比增加，频率响应曲线硬化的趋势和不稳定区域并不总是单调递增的；当模型中刚度比增大到某一临界值时，频率响应曲线和不稳定区域分别趋向于软化和增大，但当刚度比超过该临界值时，响应开始减小；对于倾斜角度的增加，索的频率响应曲线硬化的趋势和不稳定区域都是单调递增的.

/ References：

[1] Warminski J. Nonlinear normal modes of a self-excited system driven by parametric and external excitations[J]. Nonlinear Dynamics, 2010, 61(4):677-689.

[2] Zhang He, Xie Xu, Zhao Junliang. Parametric vibration of carbon fiber reinforced plastic cables with damping effects in long-span cable-stayed bridges[J]. Journal of Vibration and Control, 2011, 17(14):2117-2130.

[3] Kang Houjun, Zhao Yueyu，Zhu Haiping. Linear and nonlinear dynamics of suspended cable considering bending stiffness[J]. Journal of Vibration and Control，2013.

[4] Kamel M， Hamed Y. Nonlinear analysis of an elastic cable under harmonic excitation[J]. Acta Mechanica，2010，214(3):315-325.

[5] Gu Ming, Ren Shuyan. Parametric vibration of stay cables under axial narrow-band stochastic excitation[J]. Journal of Structural Stability and Dynamics， 2013，13(8) :1350035-1-1350035-21.

[6] Raeesi A, Cheng S, Ting D S K. A two-degree-of-freedom aeroelastic model for the vibration of dry cylindrical body along unsteady air flow and its application to aerodynamic response of dry inclined cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 130(10):108-124.

[7] Tagata G. Harmonically forced, finite amplitude vibration of a string[J]. Journal of Sound and Vibration, 1977, 51(4):483-492.

[8] Perkins N C. Modal interactions in the non-linear response of elastic cables under parametric/external excitation[J]. International Journal of Non-linear Mechanics, 1992, 27(2):233-250.

[9] Berlioz A, Lamarque C H. A non-linear model for the dynamics of an inclined cable[J]. Journal of Sound and Vibration, 2005, 279(3/4/5): 619-639.

[10] Wang Lianhua, Zhao Yueyu. Large amplitude motion mechanism and non-planar vibration character of stay cables subject to the support motions[J]. Journal of Sound and Vibration, 2009, 327(1/2): 121-133.

[11] Macdonald J H G, Dietz M S, Neild S A, et al. Genera-lised modal stability of inclined cables subjected to support excitations[J]. Journal of Sound and Vibration, 2010, 329(21): 4515-4533.

[12] Luongo A, Zulli D. Dynamic instability of inclined cables under combined wind flow and support motion[J]. Nonlinear Dynamics, 2012, 67(1): 1-17.

[13] Caetano E,Cunha A,Taylor C A.Investigation of dynamic cable-deck interaction in a physical model of a cable-stayed bridge: part I modal analysis[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(4):481-498.

[14] Caetano E, Cunha A, Taylor C A. Investigation of dynamic cable-deck interaction in a physical model of a cable-stayed bridge: part II seismic response[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(4):499-521.[15] Georgakis C T, Taylor C A. Nonlinear dynamics of cable stays: part 1 sinusoidal cable support excitation[J]. Journal of Sound and Vibration, 2005, 281(3/4/5):537-564.

[16] Georgakis C T, Taylor C A. Nonlinear dynamics of cable stays: part 2 stochastic cable support excitation[J]. Journal of Sound and Vibration, 2005, 281(3/4/5):565-591.[17] Caetano E, Cunha A, Gattulli V, et al. Cable-deck dynamic interactions at the International Guadiana Bridge: on-site measurements and finite element modelling[J]. Structural Control & Health Monitoring, 2008, 15(3):237-264.

[18] Kang Zhan, Zhong Wanxie. Numerical study on parametric resonance of cable in cable stayed bridge[J]. China Civil Engineering Journal，1998, 31(4): 14-22.(in Chinese) 亢 战, 钟万勰. 斜拉桥参数共振问题的数值研究[J]. 土木工程学报, 1998, 31(4): 14-22.

[19] Luo Shuai, Liu Hongjun, Wang Gang. The characteristic of stay-cable damping system in consideration of bridge deck vibration[J]. Journal of Shenzhen University Science and Engineering，2010, 27(4): 470-474.(in Chinese) 罗 帅, 刘红军, 王 刚. 考虑桥面运动的斜拉索减振模型[J]. 深圳大学学报理工版, 2010, 27(4): 470-474.[20] Zhou Dai, Liu Jie, Guo Junhui, et al. Vibration response of cables in cable-stayed spatial structures under axial excitaiton[J]. Engineering Mechanics, 2007, 24(3):34-41.(in Chinese) 周 岱, 柳 杰, 郭军慧，等. 轴向激励下斜拉索大幅振动分析[J]. 工程力学, 2007, 24(3):34-41.

[21] Li Fengchen, Tian Shizhu, Ou Jinping. Study on the parameter vibration of the large-span cable-stayed bridge[J]. Journal of Shenyang Jianzhu University Natural Science, 2008, 24(5): 737-742.(in Chinese) 李凤臣, 田石柱, 欧进萍. 大跨度斜拉桥拉索的参数振动[J]. 沈阳建筑大学学报自然科学版, 2008, 24(5): 737-742.

[22] Wei Minghai, Xiao Yiqing, Liu Haitao. Bifurcation and chaos of a cable-beam coupled system under simultaneous internal and external resonances[J]. Nonlinear Dynamics，2012, 67(3): 1969-1984.

[23] Zhou Haibing. The experimental investigation on nonlinear dynamics of cable-beam structure[D].Changsha: Hunan University，2007.(in Chinese) 周海兵. 索-梁组合结构非线性线性动力学实验研究[D]. 长沙：湖南大学，2007.

[24] Xia Yong, Zhang Jing, Xu Youlin, et al. Parametric oscillation of cables and aerodynamic effect[J]. Frontiers of Architecture and Civil Engineering in China, 2010,4(3):321-325.

[25] Xu Y L, Ko J M, Zhang W S. Vibration studies of Tsing Ma Suspension Bridge[J].Journal of Bridge Engineering, 1997,2(4):149-156.

[26] Warnitchai P, Fujino Y, Susumpow T. A nonlinear dynamic model for cables and its application to a cable-structure system[J]. Journal of Sound and Vibration, 1995, 187(4): 695-712.

[27] Kevorkian J, Cole J D. Perturbation methods in applied mathematics[M]. New York(USA): Springer-Verlag, 1981.

【中文责编：坪 梓；英文责编：之 聿】

2014-09-11；Accepted：2015-03-24

Coupled vibration model of cables and its parameter analysis

Liu Haitao1, Wei Minghai2†, Lin Kun1, and Xiao Yiqing1

1) Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, P.R.China 2) Department of Construction and Engineering Management, Shenyang Jianzhu University, Shenyang 110168, P.R.China

Considering the effects of cable-supported structures on cable parametric vibration, this paper presents an analysis of nonlinear parametric vibration and the chaotic dynamics of a cable using a coupled cable-beam model in which both the coupled behavior between the beam and the cable and the geometric nonlinearities of the cable are taken into account. By applying the multiple scale method to the model directly, we obtain the frequency response of cables and stability conditions. The effects of the mass ratio, stiffness ratio, and the inclined angle of the coupled model are then evaluated. The results show that the property of nonlinear parametric vibration of cables is not increasing monotonously with the mass and stiffness ratios. There is a critical value that maximizes the property of nonlinear parametric vibration of cables, and the property of nonlinear parametric vibration of cables increases monotonously with the inclined angle.

structural mechanics; cable-supported structures; cable; coupled model; frequency response; parametric vibration; nonlinear vibration

：Liu Haitao, Wei Minghai, Lin Kun, et al. Coupled vibration model of cables and its parameter analysis[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(3): 231-238.(in Chinese)

TU 311.3

A

10.3724/SP.J.1249.2015.03231

国家自然科学基金资助项目(51078119)；国家山区公路工程技术研究中心开放基金资助项目(gsgzj-2013-03); 桥梁结构抗震技术交通行业重点实验室开发基金资助项目(201301)

刘海涛(1982—)，男(汉族)，山东省曹县人，哈尔滨工业大学深圳研究生院助理实验师．E-mail：liuhaitao@hitsz.edu.cn

Foundation：National Natural Science Foundation of China(51078119)；Fund of National Engineering and Research Center for Highways in Mountain Area (gsgzj-2013-03) ；Fund of Key Laboratory of Bridge Earthquake Resistance Technology, Ministry of Communications(201301)

† Corresponding author：Lecturer Wei Minghai. Email: hitsz.civil@gmail.com.cn

引 文：刘海涛，魏明海，林 坤，等．斜拉索耦合振动模型及其参数分析[J]. 深圳大学学报理工版，2015，32(3)：231-238.