基于市道轮换模型的SHIBOR市场利率

柳向东，郭 慧

暨南大学统计学系，广州 510632

【数学 / Mathematics】

基于市道轮换模型的SHIBOR市场利率

柳向东，郭 慧

暨南大学统计学系，广州 510632

基于固定波动率模型和广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity，GARCH)模型，研究引入马氏市道轮换模型. 该模型可以将线性利率期限结构推广到非线性形式，运用到资产定价的变化中，特别是债券收益率的确定中.不同于唯一依赖利率水平的传统模型,马氏市道轮换模型能够模拟货币政策对利率的影响.利用2006-10-08至2013-03-29每周三上海银行间同业拆放利率(Shanghai interbank offered rate，SHIBOR)月度数据，用R语言实现并比较了固定波动率模型、GARCH模型以及混合GARCH马氏市道轮换模型对各参数的估计效果.结果表明，混合GARCH马氏市道轮换模型的拟合效果在各种情形下均占优.

应用统计数学；马氏市道轮换；广义自回归条件异方差；上海银行间同业拆放利率；利率期限结构；固定波动率；单机制模型

在资产定价中，利率期限结构模型是一个重要的模型，一般采用债券定价中即期利率的扩散模型对其进行研究. Chan等[1]提出了一个统一的单因子线性扩散模型(CKLS)，通过实证表明一些著名的单因子模型不能有效描述短期利率行为，如 Vasicek和 CIR 模型[2-3]. Clifford等[4-9]也认为使用扩散模型进行数据拟合结果往往不甚理想. Stephen等[10-15]认为，应由一个非线性的市道轮换模型来解释多因素(牛市和熊市)带来的经济体制的变化，如美联储在20世纪80年代初发生的经验体制变化及石油输出国组织(organization of petroleum exporting countries，OPEC)在20世纪70年代末石油危机下产生的经济体制变化等.近年来，国内不少学者也开始提出并使用各种基于市道轮换的利率模型来刻画利率的动态特性.刘金全等[16]通过在利率期限结构中加入马尔科夫市道轮换，推广出与状态相依的CKLS模型，提出不同到期日利率期限结构可由缩压的马尔科夫市道轮换CKLS模型获得.吴吉林等[17-18]在市道轮换随机波动模型基础上，引入非线性漂移项，并同时考虑了随机波动方程中的常数项、滞后一阶项及方差的市道轮换模型.唐晓彬[19]在状态空间模型中引入马尔科夫市道轮换，较好地刻画了我国经济周期的非对称性，得出宏观调控政策会对我国经济产生正向的冲击，宏观调控是有效的. Wu等[20-21]把利率期限结构与马氏市道轮换结合起来进行模型研究.Zeng等[22]在市道轮换扩散模型中加入跳扩散，提出了一个动态利率期限结构模型，指出市场存在跳跃风险和市道轮换的风险,但并未做实证分析.

本研究把市道轮换模型与广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity，GARCH)模型相结合，对上海银行间同业拆放利率(Shanghai interbank offered rate，SHIBOR)进行建模.这样做是由于在不同的经济体制下会产生不同的利率波动，而马氏轮换模型能对这些不同的经济体制进行明确的研究.在某种意义上,马尔科夫市道轮换模型可被视为传统线性模型进行非线性推广的自然模式之一.本研究发现银行7天同业拆借利率存在明显的非线性、市道轮换和波动的水平效应,而且引入市道轮换后波动的持久性显著下降，可见市道轮换模型确实适用于SHIBOR市场研究.在估计技术方面，本研究采用极大似然方法估计市道轮换模型.与其他方法相比，极大似然方法所使用的计算量较少，且能用R语言来实现对各个参数的估计.不过，这种方法可能不如粒子滤波马尔科夫链蒙特卡洛方法(particle Markov chain Monte Carlo methods，PMCMC)准确有效，这是将来需要改进的一个方向[23-25].

1 动态利率波动模型

用于解释动态短期利率的模型有3类：第1类是扩散模型，主要用于建立长期的模型结构；第2类是自回归条件异方差(autoregressive conditional heteroscedasticity，ARCH)模型，该模型对金融时间序列的动态建模有用；第3类是允许存在市道轮换的马氏轮换模型.

1.1 扩散模型

大部分期限结构模型都假定短期利率随时间推移成为扩散过程.扩散模型的好处在于短期利率的瞬时变化可被描述为一个随机微分方程(stochastic differential equation， SDE)，然后利用伊藤微积分描述期限结构.Chan等[1]研究表明，许多特定的随机微分方程可写为

(1)

其中，r表示时间t内的短期利率;α和β是刻画利率变化条件均值的参数;σ为利率波动;γ度量波动对利率水平的敏感度(或称弹性参数); dB是一个标准的布朗运动.

为实现一般随机微分方程(stochastic differential equation，SDE)的校准，对式(1)进行简单的离散化处理，

Δrt=α+βrt-1+εt

(2)

1.2 广义ARCH模型

由Robert[26]提出的ARCH(autoregressive conditional heteroscedasticity)模型，经Tim[27]拓展，发展为广义ARCH模型(generalized autoregressive conditional heteroscedasticity，GARCH). 在GARCH(1， 1)模型中， 一个时间序列过程的条件均值和条件方差会被同时模拟， 其中, (1,1)指阶数为1的GARCH项(括号中第1项)和阶数为1 的ARCH项(括号中第2项)，一般来说，GARCH(1， 1)能较好地捕捉波动的聚集性，其波动率是一个由滞后的波动率估计值和滞后的预测误差平方得到的函数，

Δrt=Xt-1β+εt

(3)

需要注意的是，在短期利率GARCH(1,1)模型中，通常假定α0>0,α1≥0,β1≥0，以确保条件波动非负.此外，还假设α1-β1<1以保证条件波动过程的平稳性.

1.3 马氏市道轮换GARCH模型

近年来，计量经济学家已经对各种经济时间序列作为市道轮换的时间序列过程进行建模.在这些模型中，该变量的分布被假设在一个特定的市道或状态发生的条件下.当经济发生市道轮换时，将发生一系列的重大变化.James[28]提出的马氏市道轮换模型中，未观测到的市道随着时间的推移演变为一阶马尔科夫过程. 一些研究将马尔科夫市道轮换方法引入到波动率过程中，从而可以捕捉波动率存在的内生变化过程，如Hamilton等[29-34]考虑了马氏市道轮换的GARCH类模型.

离散扩散和GARCH模型都可写为

(4)

其中，θμ和θh是未知参数的向量；zt是独立同分布的，且其均值为0，方差为1，这2个模型中都有

μ(θμ,Φt-1)=μt=α+βrt-1

(5)

其中，θμ={α,β}.

在离散扩散模型中，条件方差是

(6)

其中，θh={σ2,γ}.

在GARCH中，条件方差是

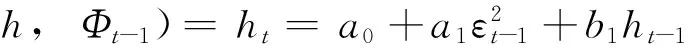
(7)

其中，θh={a0,a1,b1}，a0、a1和b1均为待估参数.

一般市道轮换(general regime switching，GRS)模型的形式为

Δrt=μ(θμ(St),Φt-1)+

(8)

其中，St是t时刻的未知市道.本研究中，St取值1或2.尽管原则上这个方法能够很容易地被扩展到多个市道中，但为了注释方便，当St=i时，式(8)可以写成

(9)

其中，μit是一个漂移项. 假设在每个市道下短期利率条件正态，那么在市道为1时，Δrt的分布是N(μ1t,h1t)， 市道为2时， Δrt的分布是N(μ2t,h2t)， 可以写成

(10)

其中，p1t=Pr(St=1|Φt-1)， 表示市道1发生的可能性，其t时刻的变化条件方差为

[p1tμ1t+(1-p1t)μ2t]2

(11)

这里ht不是轨道相关的，在服从GARCH过程的h1t+1和h2t+1的构造中能够被用作滞后条件方差，即

(12)

[p1t-1μ1t-1+(1-p1t-1)μ2t-1)]2

(13)

εt-1= Δrt-1-E[Δrt-1|Φt-1]=

Δrt-1-[p1t-1μ1t-1+

(1-p1t-1)μ2t-1]

(14)

在一般模型中，条件均值采用标准的均值回归形式，因此

μit=αi+βirt-1

(15)

市道轮换模型允许经济体在任意时刻存在任意有限的不同市道，市道完全支配该系列的动态行为.在马氏轮换模型中，每个市道都是计量经济学家无法直接观察得到的，因此，必须利用统计推断得到在任意时刻各个市道发生的可能性.由此James[28]开发了一个过滤器，它使得计量经济学家能够运用迭代的方法来推断每个时间点的市道发生的概率.

本研究用一个恒定的转移概率矩阵来计算马氏轮换模型，

(16)

由式(11)、式(15)和式(16)，对数似然方程可变为

(17)

(18)

其中，P和Q均为转移概率；g1t=f(Δrt|St=1)；g2t=f(Δrt|St=2).

初始状态在市道1的发生概率为

(19)

这个模型超越了基本扩散模型和基本的GARCH模型，因为基本的扩散模型和基本的GARCH模型的参数估计是在单机制的假设前提下进行的.如果有2个市道，即高波动和低波动市道的情况下，简单地假定在一个波动恒定的样本期间内，将会系统性地高估低波动市道时的波动率和低估高波动市道时的波动率.

2 模型实证研究

本研究数据取自每周三SHIBOR月度数据，包括2006-10-08至2013-03-31日数据，共计334个观测值.

2.1 固定波动率模型的估计与对比分析

根据固定波动率的一阶马氏市道轮换模型，短期利率的变化在市道i中服从N(a0i+a1irt-1,b0i)分布，对比分析单机制和市道轮换的固定波动率模型.表1给出了单机制和马氏市道轮换的固定波动率模型参数的估计结果及相应的检验统计量.其中，参数rt为t时的短期利率；a0i是利率均值回复水平；a1i为均值回归参数；b0i为短期利率的波动率.可见，在各个市道中方差都是固定不变的，因此该模型称为固定波动率模型.

在市道轮换固定波动率模型中,

(20)

在单机制固定波动率模型中,

Δrt|Φt-1～N(a01+a11rt-1,b01)

(21)

用极大似然估计法分别对单机制和市道轮换固定波动率模型中的参数进行估计，结果如表1. 其中，t和p是基于一致异方差的标准误差；P和Q的显著性是相对于0.5而言.

表1 单机制和市道轮换的固定波动率 模型参数估计及统计分析Table 1 Parameter estimation and related statistics with single-regime model and Markov regime-switching constant-variance model

注：1)、2)和3)分别表示在0.1%、1%和5%水平下显著.

在市道轮换固定方差模型中，市道1的方差与市道2的方差有明显差别. 市道1的特点是一段时间内的低方差(低波动率)和低利率——隐含的长期均值为每年2.43.市道2表现为一段时间内的高方差(高波动率)和高利率——隐含的长期均值为每年4.24.其中，2个市道都有强持续性(P值和Q值都超过0.8，且都显著).在此模型中，Ljung-Box检验的结果表明，残差序列相关性已明显下降.通过对比表明，在SHIBOR数据中，这个简单的马氏市道轮换模型比单机制模型能更好地描述短期利率随机波动率的特征.

2.2 GARCH模型的估计与对比分析

下面放宽各个市道中波动率固定的假设，研究允许条件波动率存在的GARCH过程.表2给出了单机制和马氏市道轮换的GARCH模型参数的估计结果及相应的检验统计量.其中，t和p是基于一致异方差的标准误差；P和Q的显著性是相对于0.5而言；参数a0i和a1i与表1相同；hit为市道i时的波动率；b0i、b1i和b1i为系数.

表2 单机制和马氏市道轮换的GARCH模型 参数估计及统计分析Table 2 Parameter estimation and related statistics with single-regime model and Markov regime-switching GARCH models

注： 1)、2)和3)分别表示在0.1%、1%和5%水平下显著.

在混合GARCH马氏市道轮换模型中，

(22)

(23)

εt-1=Δrt-1-[p1t-1μ1t-1+(1-p1t)μ2t-1]

(24)

μit-1=α0i+a1irt-1

(25)

在单机制GARCH模型中，

Δrt|Φt-1～N(a01+a11rt-1,h01)

(26)

在单机制GARCH模型中，隐含的长期均值是每年2.34，比单机制固定波动率模型小.尽管在此模型中Jarque-Bera检验仍不支持标准化残差服从标准正态分布的假设，但Ljung-Box的检验结果比单机制固定方差模型有改善，因此GARCH模型比单机制固定方差模型优异.

在混合GARCH马氏市道轮换模型中，同样地，市道1为高波动率的机制，市道2为低波动率的机制.此外，高波动率市道与低波动率市道比较时，高波动性市道对近期震荡更敏感(b11>b12). 在此模型中，Ljung-Box检验的结果已几乎无法表明残差平方项的序列仍存在相关性. 显然，与其他模型对比，混合GARCH马氏市道轮换模型能更好地刻画SHIBOR利率随机波动的特征.

结 语

本研究比较了固定波动率模型、GARCH模型和混合GARCH马氏市道轮换模型的拟合效果，所有模型的估计，都使用R语言编程实现.实证研究表明，GARCH模型比固定方差模型好，市道轮换模型比单机制模型优，混合GARCH马氏市道轮换模型对SHIBOR利率风险溢价的估计具有更卓越的能力.未来研究可尝试在高频数据中加入市道轮换或基于市道轮换模型拓展出各种风险管理的方法，并用PMCMC方法对高频数据进行参数估计[34]，这些方法对微观经济规律的研究和应用具有重要的意义.

/ References：

[1] Chan K, Karolyi A, Longstaff F, et al. An empirical comparison of alternative models of the short-term interest rate[ J]. Journal of Finance, 1992, 47(3):1209-1227.

[2] Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics, 1977, 5(2):177-188.

[3] Cox J, Ingersoll Jr J, Ross S. A theory of the term structure of interest rates[J]. Econometrica, 1985, 53(2):385-407.

[4] Clifford A B, Walter N T．The stochastic volatility of short-term interest rates: some international evidence[J]．The Journal of Finance, 1999, 54(6):2339-2359．

[5] Xiong Jie，Zeng Yong. A branching particle approximation to the filtering problem with counting process observations[J]. Statistical Inference for Stochastic Processes, 2011，14(4): 111-140.

[6] Del M P, Doucet A，Jasra A. On adaptive resampling procedures for sequential Monte Carlo methods[J]. Bernoulli, 2012，18(1): 252-278.

[7] Lopes H F，Tsay R S. Particle filters and Bayesian inference in financial econometrics[J]. Journal of Forecasting, 2011，30(1): 169-209.

[8] Douc R，Moulines E. Limit theorems for weighted samples with applications to sequential Monte Carlo methods[J]. The Annals of Statistics, 2008，36(2): 2344-2376.

[9] Asparouhova E N, Bessembinder H，Kalchevab I. Liqui-dity biases in asset pricing tests[J]. Journal of Financial Economics, 2010，96(3): 215-237.

[10] Stephen F G. Regime-switching in Australian short-term interest rates[J].Accounting & Finance，1996，36(1)：65-88．

[11] Liu Xiangdong, Zhong Nie. Pricing life insurance with jump Poisson-diffusion under no-arbitrage framework [J].International Journal of Applied Mathematics and Statistics, 2014, 52(4):53-62.

[12] Liu Xiangdong, Shu Wu, Yong Zeng. The multifactor term structure of interest rates under regime shifts and Lévy jumps[J].The 8th ICSA International Conferrence,2010,56(4):852-872.

[13] Ait-Sahalia Y, Kimme R. Estimating affine multifactor term structure models using closed-form likelihood expansions [J]. Journal of Financial Economics, 2010, 98(3): 113-144.

[14] Xiang Ju, Zhu Xiaoneng. A regime-switching Nelson-Siegel term structure model and interest rate forecasts [J]. Journal of Financial Econometrics,2013, 11(3):522-555.

[15] Siu T K. Bond pricing under a Markovian regime-switching jump-augmented Vasicek model via stochastic flows[J]. Applied Mathematics and Computation, 2010, 216(3):3184-3190.

[16] Liu Jinquan, Zheng Tingguo. The term structure of interest rates to regime-switching model and the empirical analysis[J]. Economic Research, 2006, 41(11): 82-91.(in Chinese) 刘金全，郑挺国.利率期限结构的马尔科夫机制转移模型与实证分析[J]．经济研究，2006，41(11)：82-91．

[17] Wu Jilin, Tao Wangsheng. The research of short-term interest rates in our country based on the regime-switching and random fluctuations[J]. Chinese Management Science, 2009, 17(3): 40-46.(in Chinese) 吴吉林，陶旺升．基于机制转移与随机波动的我国短期利率研究[J].中国管理科学，2009，17(3)：40-46．

[18] Smith D R. Markov-switching and stochastic volatility diffusion models of short-term interest rates[J].Journal of Business and Economic Statistics，2002，20(2)：183-197．

[19] Tang Xiaobin. The state space model of markov regime-switching and its application research on the economic cycle[D]. Chengdu:Southwestern University of Finance and Economics, 2010.(in Chinese) 唐晓彬．Markov机制转移的状态空间模型及其在我国经济周期中的应用研究[D]．成都：西南财经大学，2010.

[20] Wu Shu，Zeng Yong. A general equilibrium model of the term structure of interest rates under regime-switching risk[J]. International Journal of Theoretical and Applied Finance, 2005, 8(7):839-869.

[21] Wu Shu, Zeng Yong. An econometric model of the term structure of interest rates under regime-switching risk[J]. Springer, 2013，2:53-59.

[22] Zeng Yong, Wu Shu. The term structure of interest rates under regime shifts and jumps[J].Economics Letters, 2006, 93(2):215-221.

[23] Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods[J]. Journal of the Royal Statistical Society(Series B), 2010, 72:269-342.

[24] Le A, Dai Qiang, Singleton K. Discrete-time dynamic term structure models with generalized market prices of risk[J]. Review of Finance Studies,2010, 32(1):2184-2227.

[25] Futami H. Regime switching term structure model under partial information[J]. International Journal of Theoretical and Applied Finance, 2011, 14(2): 265-294.

[26] Robert F E. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J].Econometrica, 1982,50(4):987-1007.

[27] Tim B. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1986, 31(3):307-327.

[28] James D H. A new approach to the economic analysis of nonstationary time series and the business cycle[J]. Econometrica, 1989, 57(2):357-384.

[29] Hamilton J D, Susmel R. Autoregressive conditional heteroscedasticity and changes in regime[J]. Journal of Econometrics, 1994,64(2):307-333.

[30] Ferland R, Gauthier G, Lalancette S. A regime-switching term structure model with observable state variables [J]. Finance Research Letters, 2010, 7(2):103-109.

[31] Elliott R J, Siu T K. On Markov-modulated exponential-affine bond price formulae [J]. Applied Mathematical Finance, 2009, 16(1): 1-15.

[32] Dai Qiang, Singleton K, Yang Wei. Regime shifts in a dynamic term structure model of the U.S. treasury bond yields [J]. Review of Financial Studies, 2007, 20(2): 1669-1706.

[33] Ang A, Bekaert G, Wei Min. The term structure of real rates and expected inflation [J]. The Journal of Finance, 2008, 63(2):797-849.

[34] Zhu Cai, Huang Jianhui. State-space models: application in economic and finance[M]. New York(USA)：Springer，2013.

【中文责编：坪 梓；英文责编：木 南】

2014-12-17；Accepted：2015-01-26

Research of market interest rates of the SHIBOR based on regime switching model

Liu Xiangdong†and Guo Hui

Department of Statistics, Jinan University, Guangzhou 510632, P.R.China

In this paper, a new model, the Markov regime switching model, based on the fixed volatility model and the generalized autoregressive conditional heteroskedasticity (GARCH) model is introduced. In the Markov regime switching model, the linear term structure of interest rates can be extended to nonlinear form. The Markov regime switching model can be used to estimate the dynamics of asset prices, especially the bond yields. Different from the traditional model, which only depends on the level of interest rates, a state variable is introduced in the regime switching model, and thus the model can indicate the impact of the monetary policy on interest rates . Using the monthly Shanghai interbank offered rate (SHIBOR) data issued every Wednesday from October 8th, 2006 to March 29th, 2013, we use R implement and compare the performances of fixed volatility model, GARCH model, and the mixed GARCH Markov regime switching model in estimating the monthly SHIBOR. The results indicate that the mixed GARCH Markov regime switching model can make good estimations and can be considered as the best one under all circumstances.

application of statistical mathematics; Markov regime switching; generalized autoregressive conditional heteroskedasticity (GARCH); Shanghai interbank offered rate (SHIBOR); term structure of interest rates; fixed volatility; single regime model

：Liu Xiangdong，Guo Hui. Research of market interest rates of the SHIBOR based on regime switching model[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(3): 317-323.(in Chinese)

O 211.9；F 830

A

10.3724/SP.J.1249.2015.03317

国家自然科学基金资助项目(71471075);教育部人文社会科学研究资助项目(14YJAZH052)

柳向东(1973—)，男(汉族)，湖南省浏阳市人，暨南大学副教授、博士. E-mail: tliuxd@jnu.edu.cn

Foundation：National Natural Science Foundation of China (71471075); Humanities and Social Science Foundation of Ministry of Education(14YJAZH052)

† Corresponding author：Associate professor Liu Xiangdong. E-mail: tliuxd@jnu.edu.cn

引 文：柳向东，郭 慧. 基于市道轮换模型的SHIBOR市场利率[J]. 深圳大学学报理工版，2015，32(3)：317-323.