基于线性化Poincaré映射模型的非线性电力电子系统控制方法

王 刚 侍乔明 付立军 纪 锋 陈宇航 蒋文韬

1.海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033

2.西安交通大学电气工程学院 西安 710049

0 引言

随着能源、交通、国防和生活等领域应用需求的提升和现代科学技术的进步，各种复杂电力电子变流装置的应用越来越广泛，成为独立电力系统的核心电能变换单元[1,2]。构建独立供电的非线性电力电子系统时，良好的动态性能是保证系统安全稳定运行的前提条件。动态性能指标与系统拓扑结构、元器件参数、运行方式和控制方式有关。一般说来，提高系统动态性能指标最有效和最经济的方法是采用先进的控制方法[3]。

系统控制的基础是系统动态性能分析。非线性电力电子系统有三种非线性来源：不同阶段系统拓扑结构的切换，占空比控制方法和非线性元件[4,5]。上述三种非线性因素互相耦合，无法解耦处理。陆用电力系统的稳态是平衡点，动态性能是平衡点附近的动态响应，将描述系统的非线性微分方程在平衡点线性化，对其进行特征结构分析，即可得到系统动态响应的模式和模态等信息。非线性电力电子系统的稳态是周期轨道，动态性能是周期轨道的动态响应，Poincaré映射反映的是其采样时刻离散状态变量的动态响应，而一个周期内状态变量的动态响应取决于系统的非线性微分方程。这种复杂的时变非线性特性使得非线性电力电子系统的动态性能分析比较困难，同时系统呈现出分叉和混沌等丰富的动力系统特征[4]。非线性电力电子系统的动态性能分析方法有三种：状态空间平均法、数值仿真法和Poincaré映射法。

状态空间平均法通过对各个开关工作模态做平均处理，得到变换器的近似解析模型[6,7]。这种转换是近似的，其准确度随着系统工作频率与开关频率比值的增大而降低。某些情况下即使开关频率很高，状态空间平均法仍有较大的误差，这影响了其动态性能分析的有效性和准确性[7]。

数值仿真法将非线性电力电子系统用时变非线性微分方程描述，针对特定的扰动，利用时域仿真计算系统变量完整的时域响应[8]。其缺点是：扰动和时域响应观测量的选择对结果影响很大，仿真计算耗时太多，物理概念不清晰，难以利用仿真结果找出影响动态性能的主要因素和设计系统的控制策略[9]。

Poincaré映射法将周期轨道的渐近稳定性等效为平衡点的Lyapunov稳定性，这种等效是严格的。利用周期轨道Poincaré映射可以研究系统的动态性能[4,5]。目前这种方法用于系统动态特性分析的较多，有助于理解系统中复杂的动力系统行为，但对于解决系统设计问题的指导作用有限[10,11]。因而迫切需要研究基于Poincaré映射的非线性电力电子系统控制方法。

文献[5]针对系统的三种非线性，提出了基于梯形积分法的周期轨道及其 Poincaré映射算法。文献[5，12]提出了采用1与 Poincaré映射 Jacobian矩阵谱半径的差作为系统的稳定裕度指标，该指标不仅能反映系统的稳定水平，还可以反映系统状态变量增量动态响应的衰减速度。

本文构造包含控制变量作用的周期轨道Poincaré映射，用线性化 Poincaré映射模型表示非线性电力电子系统状态变量的动态响应，以系统稳定裕度指标为目标优化控制参数，建立基于线性化Poincaré映射模型的非线性电力电子系统控制方法。

1 基于线性化Poincaré映射模型的控制

包含三种非线性来源的非线性电力电子系统模型为[5]

式中，T为开关周期；D为占空比；状态变量X为m维；控制变量U是周期为T的函数，即 ( ) ()UU。

首先确定系统（1）的周期轨道。假设状态变量在周期轨道上运行，在开关周期初始时刻kT的状态变量为X0。在开关周期第1阶段取n1个分点，第2阶段取n2个分点，令n=n1+n2，设每个分点的状态变量为X0,X1,…,Xn，控制变量为U0,U1,…,Un。用隐式梯形积分公式列写周期轨道满足的方程为

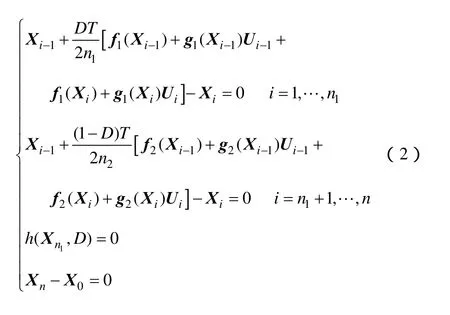
式中，未知数为X0,X1,…,Xn,D，其个数为m(n+1)+1个，方程数也是m(n+1)+1个。式（2）的初值可由状态空间平均法提供，利用Newton Raphson法求解该方程，即可得到系统的周期轨道。

式（3）是关于变量 （X0,X1,…,Xn,D）T(m(n+1)+1维)的mn+1 个方程，给定一个X0,U0,··,Un，就对应一个Xn，即确定了隐函数形式的Poincaré映射

假设系统的控制规律为

设 Poincaré映射采样时刻为开关周期开始时刻，其状态变量用上标表示，以示与一个周期内状态变量分点的区别，分别为X0,…,Xn。联立式（3）和式（5），可得开关周期开始时刻状态变量的Poincaré映射为

用Δ表示相应变量的增量，在Poincaré映射采样时刻周期轨道相应的状态点Xe处，对式（6）进行线性化得

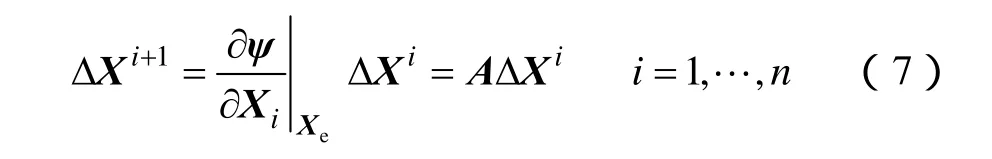
式（7）即为系统的线性化Poincaré映射模型，它包含系统控制变量的影响，将周期轨道的动态响应特性变换为平衡点为Xe的线性化动态响应特性（式（7））。注意这种变换仅是对Poincaré映射采样时刻状态变量动态响应的线性近似，并不对应所有时刻状态变量的动态响应。如果采样时刻的状态变量达到Xe，那么系统的状态变量一定进入周期轨道，因此线性化 Poincaré映射模型可以表示周期轨道的动态响应特性。

上述系统的稳定裕度为

式中，()ρA为矩阵A特征值的最大模，即A的谱半径。

系统稳定裕度不仅是系统稳定的裕度指标，而且是状态变量扰动量衰减速度的量度。其值越大，系统稳定裕度越大，状态变量扰动量的衰减越快[5,12]，系统动态性能越好。基于此，采用该指标作为系统控制性能的评价指标。

作为采用周期轨道模型控制的初步研究，假设系统控制规律（5）的函数形式已知，但相关控制系数有待确定。例如，系统的控制规律为状态反馈或PI控制。这时对于一组向量形式为K的给定控制系数，其控制性能指标Sm即可确定。对于这组系数进行优化以得到系统最大的控制性能指标Sm，这样就得到了基于线性化Poincaré映射模型的系统控制规律。

本文主要讨论基于周期轨道模型的系统控制设计方法，采用依次优化算法确定系统的控制规律，也可以采用其他优化算法。依次优化算法为：不断改变控制系数向量K的第一个分量，其他分量不变，计算系统控制性能指标Sm，使这一指标最大，从而确定K的这个分量。同理依次确定K的其他分量。再重复上述过程，直到相邻两次K差值的范数小于给定值。

2 斩波器占空比设计

采用文献[5]的带有恒功率负载的Boost闭环控制系统，除了恒功率负载的功率P=1.5W，其余电路参数不变，如图1所示。

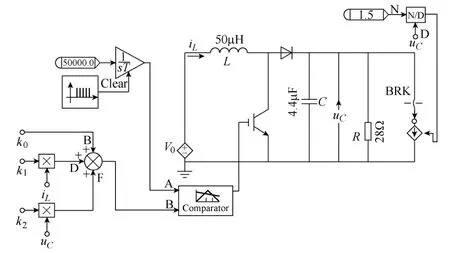
图1 Boost电路图Fig.1 Circuit diagram of Boost

电路参数如下：R=28Ω，C=4.4μF，L=50μH，开关管的导通电阻RT=0.005Ω，二级管的导通电阻Rd=0.01Ω，恒功率负载的功率P=1.5W，电源电压V0=5V，f=50kHz。设iL和uC分别为电感电流和电容电压，假定系统的占空比反馈控制规律采用状态变量反馈控制，优化其控制参数，即

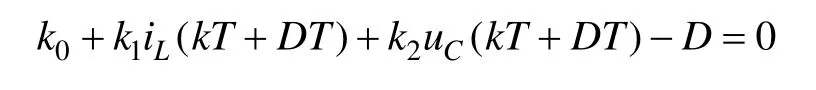
设系统初始控制参数对应的占空比方程为

取n1=2，n2=8，周期轨道对应的占空比De为0.253 8，其周期轨道如图2所示。

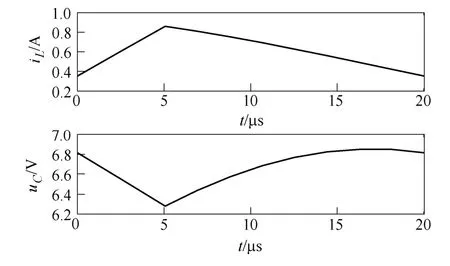
图2 Boost电路周期轨道Fig.2 Periodic orbit of Boost

利用前述算法可以计算系统周期轨道 Poincaré映射的 Jacobian矩阵N，Poincaré映射抽样时刻状态变量的微分增量对于占空比增量ΔD的 Jacobian矩阵L，则 Poincaré映射时刻状态变量的微分增量有下列关系

设系统增量形式的反馈控制为

式中，K为待定的行向量，1nΔX为系统状态切换时的状态变量增量。

同理对应于拓扑切换时的状态变量1nΔX进行微分增量计算，可得

综合式（9）～式（11），有

采用依次优化算法计算向量K，表1是本文设计方法的结果，可见采用设计控制参数，系统稳定裕度和动态响应速度有了显著提高。假定在 0.03s时电源电压V0跌落 10%，变为 4.5V。图3是用PSCAD仿真计算的Boost电路在初始控制参数和设计控制参数情况下的动态响应比较，仿真步长为0.1μs。可见采用设计控制参数，系统动态响应性能在稳态偏移、响应速度和超调量等方面都有显著的提高。

表1 Boost电路占空比设计结果Tab.1 Design results of duty ratio of Boost

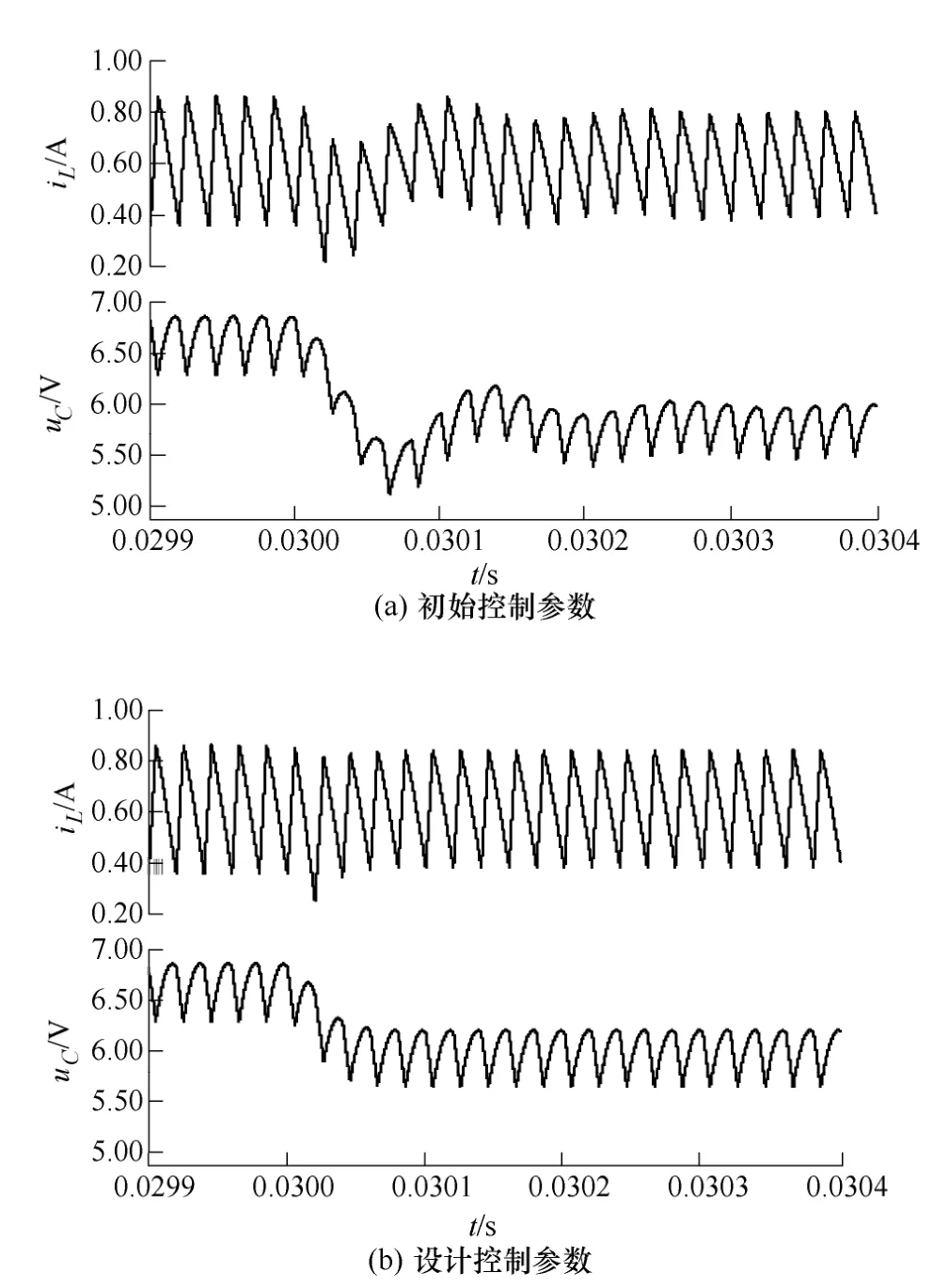
图3 Boost电路状态变量动态响应Fig.3 Dynamic response of state variables of Boost

图4是采用初始控制参数和设计控制参数，Boost电路状态变量动态响应及其线性化 Poincaré映射模型相应结果的比较。其中实线为状态变量动态响应，由式（2）和式（3）计算；虚线为线性化Poincaré映射模型的动态响应，由式（7）计算。系统状态变量的动态响应与图3一致，线性化Poincaré映射模型的状态变量动态响应可表征其映射采样时刻状态变量的动态响应。

图4 Boost线性化Poincaré映射模型状态变量动态响应Fig.4 Dynamic response of state variables of Boost by linearized Poincaré mapping model

3 不控整流发电机的励磁设计

采用文献[13]的带恒功率负载的不控整流发电机系统，除了恒功率负载的功率P=1.5kW，其余电路参数不变，如图5所示，系统参数见表2。

图5 发电机不控整流系统Fig.5 Diode rectifiers-generator system

发电机励磁采用PI控制，维持其整流输出电压udc为额定值ur=500V，如图6所示。优化其比例环节和积分环节的增益系数k1和k2。

图6 发电机不控整流系统励磁控制Fig.6 Excitation control of diode rectifiersgenerator system

表2 发电机不控整流系统参数[13]Tab.2 Parameters of diode rectifiers-generator system

假定零时刻为从VD1和VD6的导通阶段刚好进入VD1、VD2和VD6的换向阶段，这时同步发电机的转子位置为θ1，则系统的状态变量为其中id为定子d轴电流，iq为定子q轴电流，ifd为励磁绕组电流，ikd为d轴阻尼绕组电流，ikq为q轴阻尼绕组电流。

首先根据直流电压额定值确定发电机励磁电动势Ef的额定值Efe。给定一个励磁电动势，计算系统周期轨道，再计算直流电压的周期平均值。不断调整励磁电动势，直到该周期平均值为其额定值。这样就得到了励磁电动势的额定值Efe=1.01。

给定的一个Ef，系统周期轨道Poincaré映射为[13]

式中，X1和X2分别为周期起始时刻和下一个周期起始时刻的状态变量。

假定开关周期初始时刻状态变量的扰动为ΔX1，发电机励磁电动势的扰动为ΔEf，则下一个开关周期初始时刻状态变量的扰动ΔX2为

式中，M和L矩阵可由式（14）进行偏微分运算得到。励磁控制的模型为

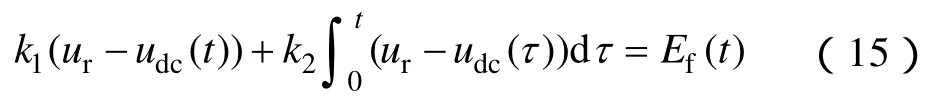
发电机不控整流系统的周期T0=1/(6fs)，fs为发电机的额定频率。假定在mT0时刻研究系统处于周期轨道上，这时的直流电压为ue，则有

下一个周期(m+1)T0时刻，有

上述两式相减得

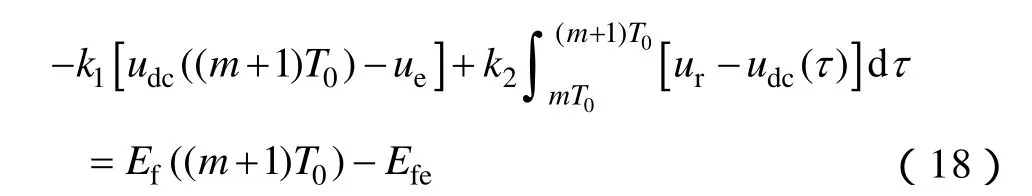
式（18）表示在[mT0,(m+1)T0]这个周期内直流电压扰动对于发电机励磁电动势Ef的影响。由于系统周期T0很小，采用梯形积分公式计算上式的积分

经过一个周期T0，发电机励磁电动势增量与状态变量增量的关系以矩阵形式表示为

式中

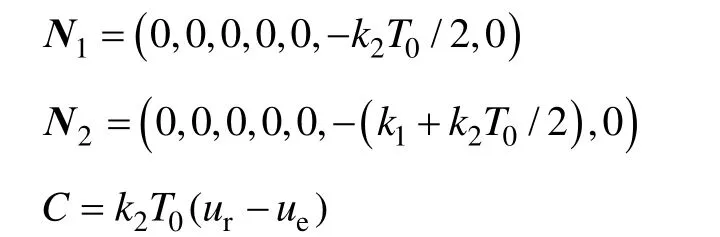
联立式（14）和式（20），可得基于线性化Poincaré映射模型的不控整流发电机励磁控制模型为

式中，E为单位矩阵。

式（2）表明励磁控制性能指标为Sm=1-ρ((E-LN)-1(M+LN))，采用依次优化算法即可21得到k1和k2的优化值。

给定两组初始励磁控制参数k1和k2，第一组为0.008 7和 0.087，第二组为 0.007和 0.07，系统稳定裕度指标Sm分别为-0.002和0.000 1，这时系统处于临界稳定的边界。利用依次优化算法计算的励磁控制参数k1和k2为 0.000 7和0.049，系统稳定裕度指标Sm为0.008 8，可见系统的稳定裕度和控制性能有了较大提升。

为了验证励磁控制对于系统状态变量动态响应的影响，假定系统带 1 364W的恒功率负荷进入稳态，在 15s时负荷忽然增加 10%（136W），达到1.5kW。采用PSCAD仿真软件计算上述三组励磁控制参数的直流电压动态响应如图7所示，仿真步长为10μs。可见采用设计控制参数，系统直流电压的动态响应性能在振荡幅度、超调量和响应速度等方面都有了显著的提高。

图7 发电机不控整流系统直流电压的动态响应Fig.7 Dynamic response of DC voltage of diode rectifiers-generator system

综合上述，基于线性化 Poincaré映射模型的非线性电力电子系统控制规律的设计流程如下：

（1）建立系统的周期轨道模型，根据控制要求，确定系统稳态时的控制变量和周期轨道，验证系统稳态性能指标符合要求。

（2）设系统控制规律对应的控制系数向量为K，建立系统周期轨道的Poincaré映射和系统的控制方程，对其进行线性化，得到相应的矩阵，推导系统的控制性能指标Sm的表达式。

（3）以性能指标Sm最大为目标，采用依次优化算法确定系统的优化控制系数向量K。

（4）考虑处于周期稳态的系统遭受小扰动，采用时域仿真方法，检验系统的动态响应是否符合要求。

4 结论

考虑控制变量扰动和Poincaré映射采样时刻系统状态变量扰动对于下一个采样时刻状态变量的影响，本文利用梯形积分法建立了包含控制变量作用的周期轨道Poincaré映射，对此进行线性化就得到了非线性电力电子系统的线性化 Poincaré映射模型，它可以表示系统状态变量的动态响应。基于该模型，以系统稳定裕度指标最大为目标，采用依次优化算法确定系统的控制参数，从而建立了基于线性化 Poincaré映射模型的非线性电力电子系统控制方法。

理论分析和仿真试验表明，本文提出的控制方法能够有效地提高非线性电力电子系统的动态响应性能，为系统控制设计提供了一条新的途径。

[1]Ma Weiming.The integrated power system in warship[C].Proceedings of the 5th International Marine Electrotechnology Conference,Shanghai,China,September 2003,1: 2-7.

[2]陈明,汪光森,马伟明.多重化双向DC-DC变换器PI滑模变结构控制策略研究[J].电力自动化设备,2008,28(4): 53-57.

Chen Ming,Wang Guangsen,Ma Weiming.PI sliding mode control strategy for multi-channel interleaved bi-directioal DC-DC converter[J].Electric Power Automation Equipment,2008,28(4): 53-57.

[3]卢强,梅生伟,孙元章.电力系统非线性控制[M].北京: 清华大学出版社,2008.

[4]Soumitro Banerjee,George C Verghese.Nonlinear phenomena in power electronics[M].New York:IEEE Press,2001.

[5]王刚,范学鑫,付立军,等.采用周期轨 Poincaré映射的非线性电力电子系统小干扰稳定性分析[J].中国电机工程学报,2012,32(1): 84-92.

Wang Gang,Fan Xuexin,Fu Lijun,et al.Small signal stability analysis of nonlinear power electronic systems based on Poincaré mapping of the periodic orbit[J].Proceedings of the CSEE,2012,32(1): 84-92.

[6]Middlebrook R D,Cuk S.A general unified approach to modeling switching-converter power stages[C].IEEE Power Electrical Systems Conference,NewYork,1976: 23-25.

[7]Brand L,Bass R M.Extension of averaging theory for power electronics systems[J].IEEE Transactions on Power Electronics,1996,11(4): 542-553.

[8]Shortt D J,Lee F C.Improved switching converter model using averaging and discrete techniques[J].IEEE Transactions on Aerospace and Electronic Systems,1983,19(2): 190-202.

[9]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京: 清华大学出版社,2002.

[10]Banerjee S.Bifurcations in two-dimensional piecewise smooth maps-theory and applications in switching circuits[J].IEEE Transactions on Circuits and Systems-1: Fundamental Theory and Applications,2000,47(5): 3100-3113.

[11]马西奎,李明,戴栋,等.电力电子电路与系统中的复杂行为研究综述[J].电工技术学报,2006,21(12): 1-11.

Ma Xikui,Li Ming,Dai Dong,et al.Reviews of research on complex behavior of power electronic circuits and systems[J].Transactions of China Electrotechnical Society,2006,21(12): 1-11.

[12]王刚,纪锋,谢桢,等.基于周期轨模型的综合电力系统逆变器性能分析[J].中国电机工程学报,2012,32(增刊): 210-216.

Wang Gang,Ji Feng,Xie Zhen,et al.Inverter performance analysis of integrated power system based on periodic orbit model[J].Proceedings of the CSEE,2012,32(Sup.): 210-216.

[13]Wang Gang,Fu Lijun,Fan Xuexin,et al.Periodic orbit model of diode rectifiers-synchronous machine system[J].Science China Technological Sciences,2013,56(1): 245-252.