计及低穿控制的混合型风电场短路电流特性与故障分析方法研究
尹 俊 毕天姝 薛安成 杨奇逊
(新能源电力系统国家重点实验室(华北电力大学)北京 102206)
0 引言
风力发电的大规模接入给电网造成的影响越来越明显,其中风力发电并网对继电保护的影响已成为当前电力系统领域备受关注的问题。随着风电场并网容量的增加,其短路电流对电力系统继电保护的影响不能再忽略不计。不精确的短路电流计算会影响故障分析的结果,进而使保护动作特性的评估产生误差。因此,有必要深入研究风电场短路电流特性,并对风电场接入后的电网故障分析方法进行研究。
目前已有文献针对风电场短路电流计算进行了研究。文献[1,2]将双馈风电场等效为一台等容量的双馈风机,并将Crowbar 投入后的双馈风力发电机组作为异步发电机处理,计算了双馈风电场的短路电流。文献[3,4]利用电气参数和输出功率求取等效风速,建立了永磁风电场的单机等效模型,并将其等效为恒功率电流源,计算了永磁风电场的短路电流。
但以上研究均未考虑风电场中风力发电机组的多样性以及故障期间控制策略对短路电流的影响。而目前风力发电机组普遍具有低电压穿越能力,在故障期间低电压穿越控制策略将对其短路电流特性造成很大影响。已有部分混合型风电场在建设过程中装配了双馈风力发电机组和永磁风力发电机组两类机组,这两类风力发电机组的短路电流特性存在较大区别。忽略控制策略与风力发电机组类型的影响会使风电场短路电流计算产生较大误差,因此有必要考虑控制策略的影响,并进一步提出含双馈风力发电机组和永磁风力发电机组的混合型风电场暂态模型。
风电场装机总量可达到几十台甚至上百台,对每台机组均详细建模,会极大地增加计算难度,因此,需在分析风力发电机组暂态模型的基础上,提出风电场的简化方法。文献[5,6]提出了以故障瞬间风力发电机组转速和桨距角动作特征为分群指标的风电场简化等效方法。但上述研究主要用于简化仿真复杂度、减少计算时间,无法给出解析模型。文献[7-9]基于风电场并网点测量值进行参数辨识,建立了风电场的辨识模型。但该研究主要用于潮流计算与稳定性分析,在稳态时具有较高的准确度,暂态时准确度较差,不适用于风电场的故障暂态过程分析。因此有必要分析风电场故障暂态特性,提出适用于短路计算的风电场简化等效方法。
此外,由于风力发电机组多样性与低电压穿越控制策略的影响使得风电场与同步发电机的故障特性存在较大区别。简单的将故障后风电场等效为同步发电机对电网进行故障分析将会产生较大误差。传统以同步发电机为基础的电网故障分析理论已难以满足风电场接入后电网故障分析的要求。
本文首先分析故障期间控制策略对风力发电机组暂态过程的影响,建立双馈风力发电机组与永磁风力发电机组的单机等效模型;在此基础上,采用分群聚合等效的方法,建立含多类型风力发电机组的风电场简化等效模型;进一步分析风电场短路电流的变化规律,给出风电场的短路电流计算方法。并采用实时数字仿真器RTDS(Real Time Digital Simulator,RTDS)建立含多类型风机的物理实验平台,验证所提短路计算方法的准确性。最后,在分析风电场简化等效模型的基础上,提出适用于风电场接入的电网故障分析方法。
1 计及控制策略影响的风力发电机组等效模型
现有风电场中风力发电机组类型主要包括双馈风力发电机组与永磁风力发电机组。为准确地分析混合型风电场故障暂态特性,需分别研究故障期间双馈风力发电机组和永磁风力发电机组的等效模型。
1.1 计及控制策略影响的双馈风力发电机组等效模型
以往研究中认为,双馈风机在故障发生后Crowbar投入,转子变流器闭锁。而我国新的风电并网标准GB/T 19963—2011《风电场接入电力系统技术规定》[10]要求,双馈风力发电机组在故障发生后,需要输出无功电流,为系统电压提供支撑,转子变流器不再闭锁。此时,变流器的输出特性将影响到双馈风力发电机组的电磁暂态特性,因此,分析双馈风力发电机组的电磁暂态特性过程,需要首先根据变流器的输入-输出外特性等效其数学模型。
在故障期间网侧变流器通过协调控制策略可将直流电压udc维持在参考值附近[11,12],因此,本文假设直流电压udc在故障前后为定值。直流电压udc经转子侧变流器逆变至励磁电压ur,ur的大小由转子变流器通过改变调制比进行控制。在考虑变流器中半导体器件电压损耗与热损的情况下,转子励磁电压的外特性方程可列写为
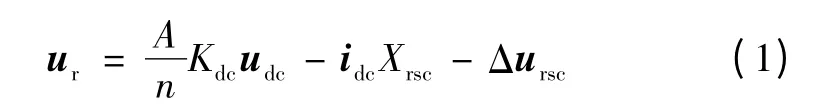
式中:A、n、Kdc分别为转子侧变流器的三相桥式电流逆变系数、定转子匝比和转子侧变流器调制比;idc、Xrsc、Δursc分别为直流母线电流、变流器等效换弧电抗和IGBT 压降。
在暂态过程中,假设转速不变,忽略磁饱和现象,定、转子采用电动机惯例,同步旋转坐标系下双馈风力发电机组空间矢量模型为[13-15]
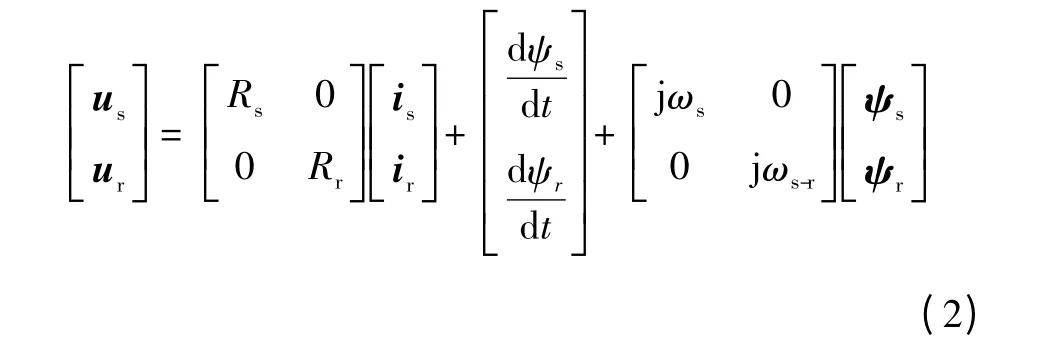
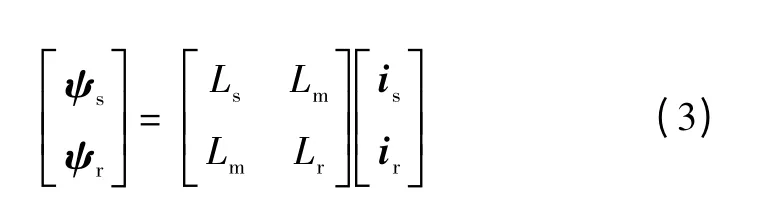
式中:us、ur、is、ir、ψs、ψr分别为折算到定子侧的定、转子电压、电流和磁链;Ls、Lr、Lm分别为定、转子电感、励磁电感;ωs、ωs-r分别为同步频率、转差角频率。
当电网发生三相短路故障,将网侧系统等效为戴维南等效电路,其中,系统侧等效电势为EL,系统到故障点的等效阻抗为Z1L,双馈风力发电机组到故障点的等效阻抗为Z2L,过度阻抗为Zf,双馈风力发电机组机端电压为us,Lsσ、Lrσ分别为定、转子漏感,Lg、Rg分别为滤波电感、电阻。根据式(1)~式(3),可得如图1所示的故障后双馈风力发电机组的等效电路。

图1 双馈风力发电机组故障后等效电路Fig.1 Fault equivalent circuit of DFIG wind generator
故障发生后,双馈风力发电机组检测到机端电压跌落后,调整转子变流器控制策略,变为低电压穿越控制模式,输出无功电流,为系统电压提供支撑。根据低电压穿越控制策略对无功支撑的要求,选取转子侧变流器的调制比Kdc改变转子励磁电压ur,进而调整转子励磁电流。最终,转子励磁电流经动态过程达到稳态的电流参考值。
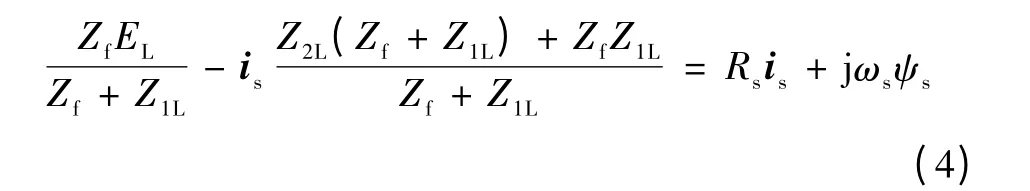
当故障达到稳态时,转子变流器励磁电流ir经过动态过程达到低电压穿越控制电流参考值ir∞。此时,定子电流也达到稳态的短路电流is∞,由式(3)和式(4)可得

式中ir∞为故障稳态时刻转子励磁电流,ir∞=ird_ref+jirq_ref,其中,irq_ref、ird_ref分别为转子有功、无功电流参考值。
则故障稳态时刻双馈风力发电机组短路电流可表示为
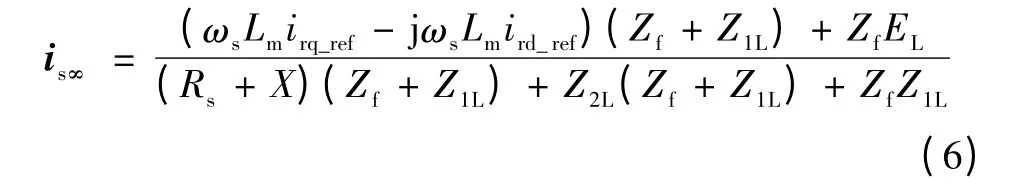
式中X 为稳态定子电抗,X=jωsLs。
由式(6)可知,双馈风力发电机组的稳态时刻短路电流由irq_ref、ird_ref、Rs、X、EL、Z1L、Z2L、Zf、Lm、ωs决定,其中,仅irq_ref和ird_ref为未知量。
电网新的并网标准规定:当电力系统发生故障引起电压跌落时,风电场在低电压穿越过程中应具备以下无功支撑能力,即当并网节点电压跌落处于标称电压的20%~90%区间内时,风电场应能通过无功电流支撑电压恢复,其注入电力系统的无功电流I ≥1.5(0.9 -Us)IN。据此可知故障后转子励磁电流的控制参考值的d、q 轴分量可分别表示为

式中:irN、irmax分别为转子额定电流和变流器最大限流电流;Kd为无功电流增益系数。
可由故障前工况求取转子电流初始值ird0、irq0。故障前双馈风力发电机组输出的有功、无功功率分别为
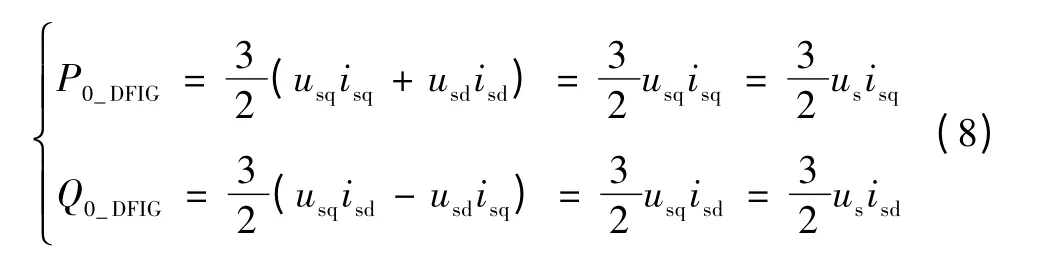
式中:isd、isq分别为定子电流的无功、有功分量;usd、usq分别为定子电压的d、q 轴分量;P0_DFIG、Q0_DFIG分别为故障前双馈风力发电机组输出的有功、无功功率。

根据式(8)和式(9),消去定子电流,可将初始时刻的转子电流与故障前双馈风力发电机组输出的有功、无功功率以及故障前电压的关系表示为

故障前定子电压us0一般在额定值附近,有功和无功功率由故障前工况决定。由式(10)可知,ird0与irq0可由故障前双馈风力发电机组输出功率和机端电压表示。因此,式(7)可表示为

故障发生后,转子侧变流器根据式(11)调节无功电流参考值的大小,进而通过电流PI 环节调节转子励磁电流。由于有功功率的参考值P0_DFIG仅与双馈风力发电机组的输入功率有关,在故障前后不变,故按照P0_DFIG选取故障后有功电流的参考值irq_ref。而无功电流参考值ird_ref仅与机端电压跌落程度有关,因此,故障发生后,转子变流器首先调节无功电流参考值ird_ref,使其满足并网标准中无功支撑的要求,在不超过逆变器限流电流的条件下,进一步调节有功电流的参考值irq_ref。
由式(11)可知,在系统故障时,双馈风力发电机组的无功电流与风力发电机组并网节点电压偏差呈线性关系,图2为故障期间无功电流参考值与电压跌落程度间的关系图。
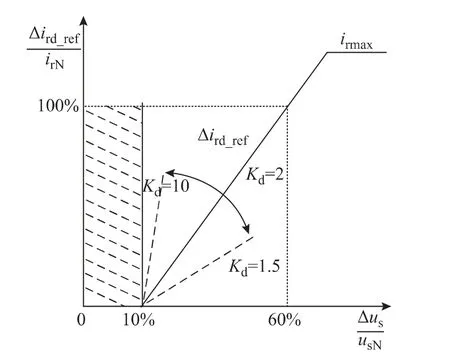
图2 无功电流参考值与电压跌落程度间的关系图Fig.2 Relationship between deviation of usand rotor reactive current
图2中,虚线区域表示控制死区,控制死区由系统正常运行时所允许的电压偏差决定。在此区域内,双馈风力发电机组的励磁电流不需要调整,而控制死区外,励磁电流按照图示曲线进行调整。当低电压穿越控制策略所提供的参考值大于转子变流器最大限流电流irmax时,按励磁电流参考值为irmax处理。由以上分析可知,在故障稳态时刻,双馈风力发电机组的稳态短路电流可由式(6)求得。
令-ωsLmirq_ref+jωsLmird_ref为双馈风力发电机组的稳态等效电势E,Z=Rs+X 为稳态阻抗,则式(5)可表示为
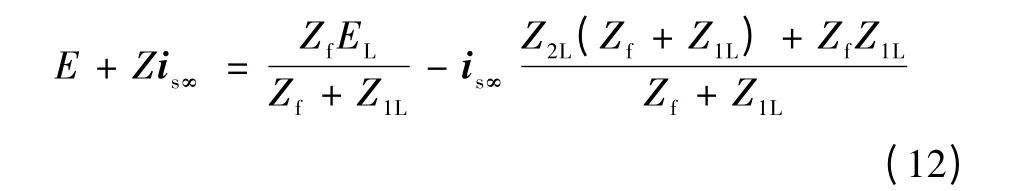
则故障稳态时双馈风力发电机组等效电路可表示为稳态等效电势E 与稳态阻抗Z 串联的形式。
1.2 计及控制策略影响的永磁风力发电机组等效模型
由于永磁风力发电机组通过全功率变流器与电网隔离,使电网的电气扰动不会直接影响到永磁风力发电机组,其短路电流暂态特性主要由故障期间网侧变流器控制策略所决定。
以往研究未计及控制策略的影响,认为故障期间永磁风力发电机组的控制参考值不发生变化,将其等效为恒定的电流源[7,8]。但新的并网标准中要求并网风力发电机组具有一定的低电压穿越能力,应能在故障期间根据电压跌落程度调整输出电流,为系统提供一定的无功支撑。因此,简单将其等效为恒定的电流源不能准确反映故障期间暂态特性。为此,本文在分析低电压穿越控制策略影响的基础上,建立永磁风力发电机组等效模型。
按风电场新的并网标准中对故障期间永磁风力发电机组输出无功支撑电流的要求,可将故障后永磁风力发电机组网侧变流器控制参考值的d、q 轴分量表示为
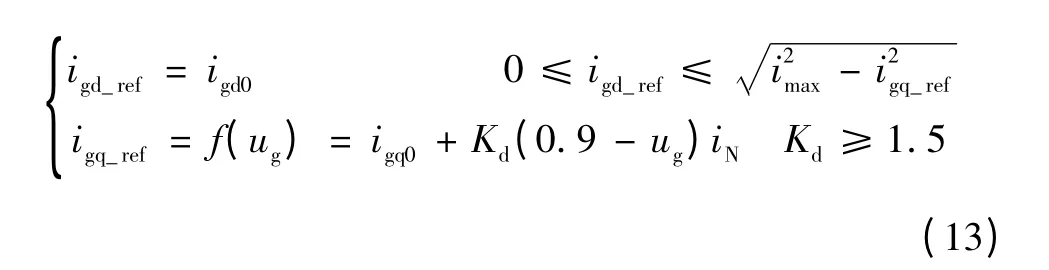
式中:igd_ref与igq_ref分别为故障后变流器输出的有功、无功电流参考值;imax为逆变器允许的最大电流;ug为永磁风力发电机组机端电压。
可由故障前工况求取网侧变流器电流初值igd0、igq0。由于永磁风力发电机组网侧变流器采用电网电压定向,即ugd=ug,ugq=0,则输出有功功率和无功功率可列写为
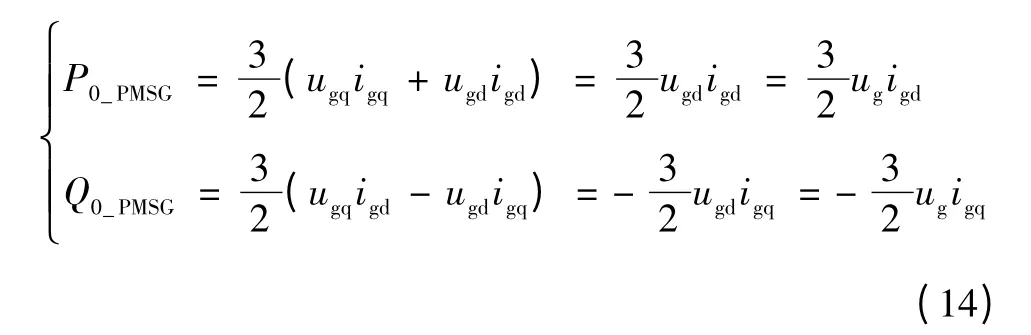
由式(14)可得网侧变流器电流初值igd0、igq0分别为

故障前永磁风力发电机组机端电压ug0一般在额定值附近,有功、无功功率由故障前工况决定。由式(15)可知,igd0与igq0可由故障前永磁风力发电机组输出功率和机端电压表示。因此,式(13)可表示为
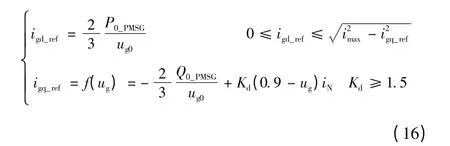
令Ig=igd_ref+jigq_ref为故障后永磁风力发电机组输出的稳态短路电流,可由式(16)求得

由式(17)可知,永磁风力发电机组输出的稳态短路电流Ig由机端电压ug以及故障前工况决定,因此,故障稳态时永磁风力发电机组等效电路可表示为一个受控电流源的形式。
2 风电场分群聚合等效
由以上分析可知风力发电机组的故障暂态特性主要受机组类型与故障期间控制策略的影响。因此,根据第1 节获得的双馈风力发电机组与永磁风力发电机组的单机等效模型,以风力发电机组类型与控制策略为分群指标,对风电场内各台风力发电机组进行分群聚合等效。
风电场内各台风力发电机组间距离较短,忽略各台风力发电机组间的线路,即各台风力发电机组连接于集电母线。图3为简化的风电场结构图,对其进行分群等效。图4为风电场分群等效电路计算流程图,按照该流程获得各台风力发电机组的等效电路。

图3 简化的风电场结构图Fig.3 Simplified structure diagram of wind farm
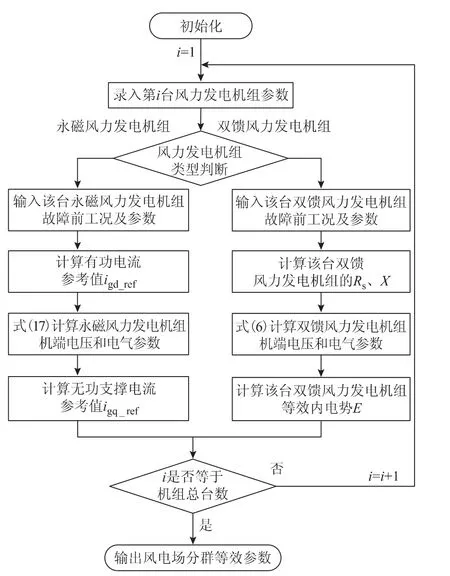
图4 风电场各分群等效电路计算流程图Fig.4 Flow chart of wind farm grouping equivalent circuit calculation
由于本文中同型机组采用了相同的控制策略,因此可由各台风力发电机组的等效电路,将故障稳态时的风力发电机组按机组类型分为2 群。由于同群的风力发电机组具有近似的暂态特性,对同群风力发电机组进行聚合等效,得到等效电势Eequ、等效阻抗Zequ、等效电流源Ig_equ。各台风力发电机组分群的等效参数可列写为

式中:Ei为第i 台双馈风力发电机组的等效内电势;ZDFIG_i为第i 台双馈风力发电机组的等效阻抗;n 为风电场中双馈风力发电机组的数量;Ig_i为第i 台永磁风力发电机组等效电流源的大小;m 为风电场中永磁风力发电机组的数量。
由式(18)可知,双馈风力发电机组机群等效模型可表示为电压源与阻抗的串联,其内电势Eequ可由各台双馈风力发电机组模型获得,其等效电抗Zequ可由各台双馈风力发电机组的电机参数求取。而永磁风力发电机组机群等效模型可表示为一个受控电流源,其电流大小为风电场中所有永磁风力发电机组等效电流的和。将双馈、永磁机群的等效模型并联接于35 kV集电线,经风电场主变压器接入220 kV 电力系统,则故障稳态时风电场可等效为图5所示的等效模型。

图5 风电场分群简化等效模型Fig.5 Simplified diagram of grouping equivalent wind farm
3 风电场短路电流计算方法
由于风电场内同型风力发电机组并接于集电母线,且同型的风力发电机组具有近似的暂态特性,可认为其在短路期间具有相同的变化规律。因此,要研究风电场短路电流变化规律,需首先分析双馈风力发电机组和永磁风力发电机组单机等效模型的短路电流变化机理。
3.1 双馈风力发电机组短路电流变化机理
如图1所示,故障期间双馈风力发电机组转子变流器通过调整其输出的转子励磁电压ur来实现低电压穿越。因此,需要分析转子励磁电压ur对短路电流变化规律的影响。
由式(3)消去转子电流得到定子磁链ψs,并将其带入式(2)的转子电压方程
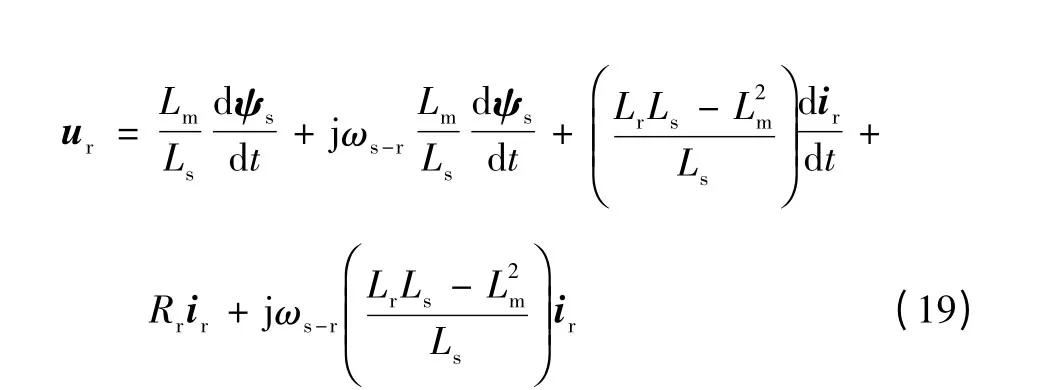
转换为转子旋转坐标系,则式(19)简化为
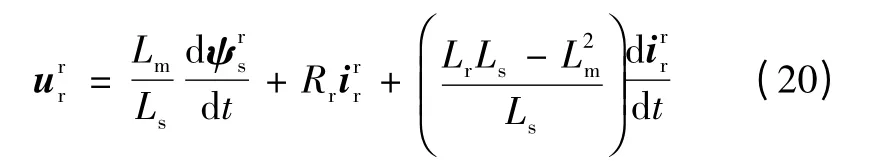
双馈风力发电机组暂态过程中转子磁链增量对发电机暂态过程的影响远大于定子磁链增量所带来的影响,且定子部分暂态过程的时间常数远小于转子部分暂态过程的时间常数,因此本文在研究双馈风力发电机组暂态过程时不考虑定子磁链暂态过程[8-11]。同时,由于变流器中IGBT 元件本身的时间常数比励磁绕组的时间常数小得多,因此忽略转子侧变流器中IGBT 的惯性时间,即Kdc在故障瞬间直接变为对应的调制比。由以上分析可知,若故障发生,则认为转子侧励磁电压由初值ur0突变至低电压穿越控制电压的参考值ur∞。由式(1)、式(20)可知,转子电流与转子励磁电压构成RL 回路,因此,故障后转子电流为转子励磁电压的阶跃响应。
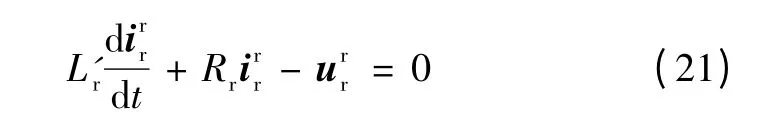
转子励磁电流的时域解可列写为
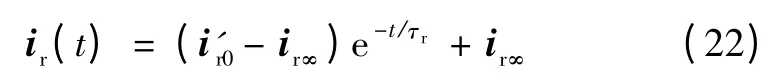
考虑到双馈风力发电机组参数中Ls=Lsσ+Lm、Lr=Lrσ+Lm,且Lm≥Lsσ、Lm≥Lrσ,则由式(3)可将定、转子电流表示为

由式(23)可知,在故障期间定子电流与转子电流具有相同的变化规律。因此,受低电压穿越控制策略影响,定子短路电流在故障期间变化机理可表示为式中分别为故障初始时刻短路电流、故障稳态时刻短路电流。
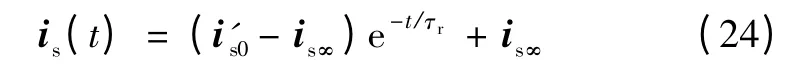
由式(24)可知,当故障发生后,各台双馈风力发电机组的短路电流由初始值按转子的时间常数τr衰减至稳态短路电流is∞。由于故障期间风电场中各台双馈风力发电机组均按式(24)的规律变化,因此可认为等效聚合后双馈机群的短路电流也具有近似的变化规律。
3.2 永磁风力发电机组短路电流变化机理
永磁风力发电机组经全功率变流器连接至电网,电网的故障扰动不会直接影响到永磁风力发电机组,其短路电流的暂态特性主要由故障期间变流器的控制策略所决定。而故障后变流器中的IGBT 元件的时间常数很小,忽略其惯性时间,即故障发生后,变流器控制参考值由初始值迅速调整为低电压穿越参考值。
通过调节变流器电流内环的PI 环节,使永磁风力发电机组输出电流的d、q 轴迅速跟上有功、无功电流参考值,可近似忽略其暂态过程。由式(16)可知,故障前后永磁风力发电机组的输出电流可表示为
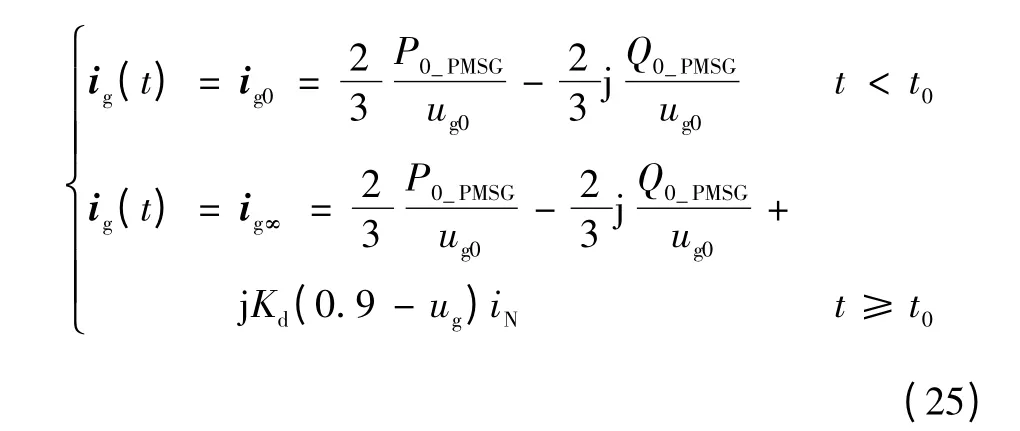
在故障期间每台永磁风力发电机组短路电流均符合式(25)所示的变化规律。因此可认为在故障期间聚合等效后的永磁机群具有相同的变化规律,其短路电流由初始值迅速变化至稳态值。
3.3 风电场短路电流计算
在建立双馈风力发电机组和永磁风力发电机组单机模型的基础上,结合分群聚合等效方法,求解各机群初始、稳态时刻的短路电流,并依据各机群短路电流的变化规律,即可求取风电场输出的短路电流。
由图5所示的风电场稳态等效模型与网侧等效电路联立可求得双馈风力发电机组和永磁风力发电机组机群故障后短路电流稳态值Is∞、Ig∞。
由式(25)可知,永磁风力发电机组机群的初始短路电流与稳态短路电流近似相等,可认为其在故障期间保持不变;而双馈风力发电机组机群的初始短路电流可根据故障初始时刻磁链不突变原则求取。
当双馈风力发电机组机端发生三相短路故障,由式(3)消去转子电流得到定子磁链
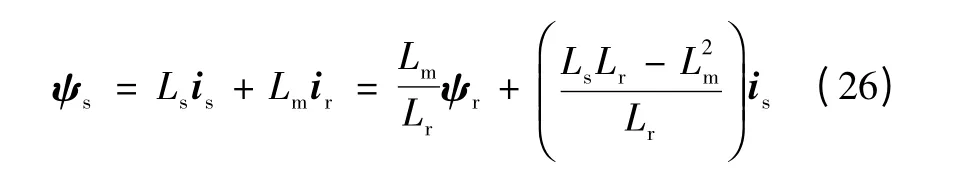
将式(26)带入定子电压方程式(2)可得
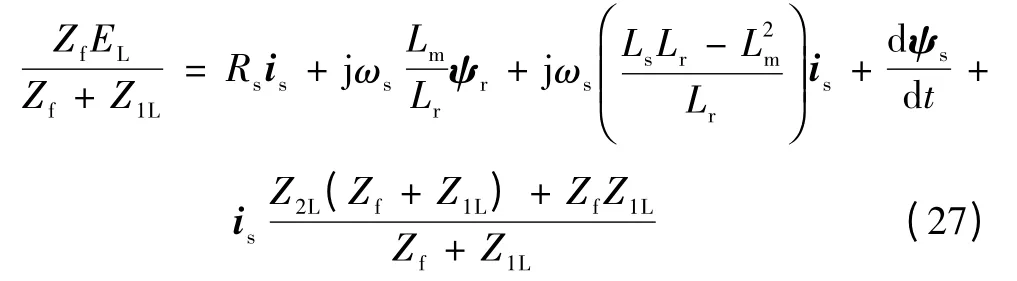
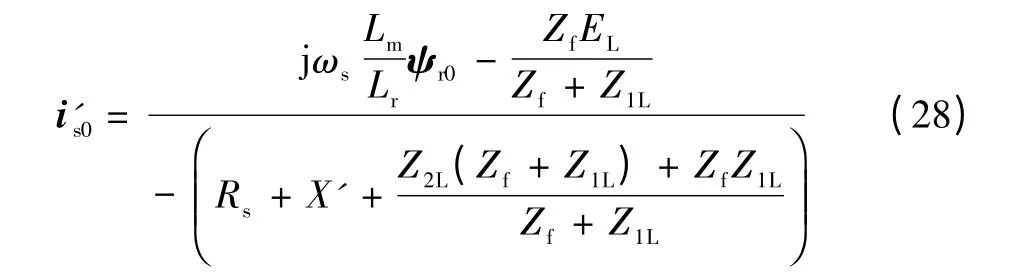
由式(28)可知,双馈风力发电机组故障初始时刻短路电流由ωs决定,其中仅转子磁链初始值ψr0为未知量,可由故障前工况求取。
根据式(8)、式(9),消去定、转子电流,可将初始时刻的转子磁链与故障前双馈风力发电机组输出的有功、无功功率以及故障前电压的关系表示为
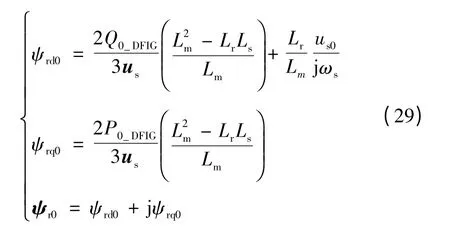
可由us0、P0_DFIG、Q0_DFIG求得故障初始时刻的转子磁链ψr0,最终将转子磁链ψr0带入式(28)计算双馈风力发电机组初始时刻短路电流i's0。
由式(24)、式(25)以及计算得到的初始电流、稳态电流可得双馈风力发电机组和永磁风力发电机组机群短路电流,进而可求得风电场出线端的短路电流。
4 短路电流实验验证
基于电力系统实时仿真设备RTDS 建立了含双馈风力发电机组和永磁风力发电机组变流器实际控制单元的物理实验平台。采用RTDS 搭建了混合型风电场的并网模型,由并行通信接口实现控制单元数据的实时传输,并以FPGA 芯片为控制内核设计了变流器物理控制单元,实现变流器的实时控制。
以图3所示的某接入电网的实际混合型风电场为例。其中各风力发电机组机通过机端变压器接于35 kV集电线,并通过风电场主变压气接入220 kV 电力系统。主要相关参数如下:风电场主变压器的电压比、短路阻抗分别为220 kV/35 kV、11%,双馈风力发电机组和永磁风力发电机组机端变压器的电压比、短路阻抗分别为35 kV/0.69 kV、3%;永磁风力发电机组22 台,单台额定容量2.0 MW,无功增益系数Kd为2;双馈风力发电机组11 台,单台额定容量2.0 MW,定子电阻和漏感分别为0.016 pu、0.169 pu,转子电阻和漏感分别为0.009 pu、0.153 pu,励磁互感为3.49 pu;线路AB、BC 段的等效阻抗分别为(0.97+j2.76)Ω、(1.46+j4.15)Ω,系统等效阻抗为j0.5 Ω。
设故障前双馈风力发电机组工作于额定工况下,以t=0.5 s时AB 线路B 端发生三相短路故障,持续0.2 s 为实验测试条件。图6a 为实验测试中获取的B 端三相短路时双馈风力发电机组DFIG1短路电流实测值。经由全周傅式算法提取了短路电流的有效值,可获得图6b 中的实测轨迹;利用所提的方法计算了短路电流有效值,获得了图6b 中的模型计算轨迹。

图6 DFIG1三相短路电流计算值与实测值比较Fig.6 Comparison between calculated value and testing result of DFIG1short circuit current
由图6b 可知,在0.5 s 发生故障时,双馈风机短路电流有效值突增到额定值的3.13 倍,本文提出的模型计算结果为3.17 pu,与实验测试的误差为1.3%。在故障稳态后,实验测试结果为额定值的2.18 倍,本文提出的方法计算结果为2.16 pu,与实验测试的误差为1.2%,且在衰减过程中的曲线拟合度极高,测试值在本文的计算曲线上下波动。由以上分析可知,本文提出方法可准确分析单台双馈风机的短路电流变化机理。
设故障前永磁风机工作于额定工况下,以t=0.5 s时AB 线路B 端发生三相短路故障,持续0.2 s 为实验测试条件。图7a 为实验测试获取的B 端三相短路时永磁风机PMSG1短路电流实测值。经全周傅式算法获得图7b 中的短路电流有效值实测轨迹。图7b 为B 端三相短路PMSG1短路电流有效值实测与计算结果比较。

图7 PMSG1三相短路电流计算值与实测值比较Fig.7 Comparison between calculated value and testing result of PMSG1short circuit current
由图7b 可知,在0.5 s 发生故障时,永磁风力发电机组短路电流有效值迅速突增到额定值的1.91 倍,本文提出的模型计算结果为1.93 pu,与实验测试的误差为1.05%。由实验结果可知,永磁风力发电机组短路电流在故障后迅速达到稳态值,且在故障期间变化很小,与前文分析得到的永磁风力发电机组短路电流变化机理一致。由以上分析可知,本文提出方法可准确分析单台永磁风力发电机组的短路电流变化机理。
图8a 为采用聚合等效模型计算得到的双馈风力发电机组机群与永磁风力发电机组机群短路电流,将聚合模型下永磁风力发电机组机群与双馈风力发电机组机群的短路电流矢量加和,可得风电场出线端的短路电流轨迹。图8b 为风电场出线端短路电流实测值,图8c 为风电场出线端短路电流有效值实测与计算结果对比图。
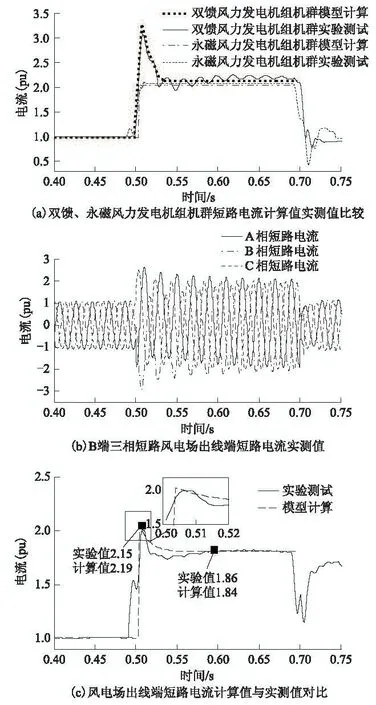
图8 风电场短路电流计算值与实测值对比Fig.8 Comparison between calculated value and testing result of wind farm short circuit current
由图8a 可知,双馈风力发电机组和永磁风力发电机组机群在聚合等效模型下获得的短路电流计算值与实测值的误差较小,且在故障发生后,由机群短路电流实测值可知,其短路电流变化规律与单机基本一致,这与前文的分析相符。
由图8c 可知,在0.5 s 发生故障时,风电场出线端短路电流有效值突增到额定值的2.15 倍,本文提出的方法计算结果为2.19 pu,与实验测试的误差为2.1%,在故障稳态后,实验测试结果为额定值的1.86 倍,本文提出的方法计算结果为1.84 pu,与实验测试的误差为1.2%。在衰减过程中的最大误差不超过5%,且测试值在本文的计算曲线附近波动。由以上分析可知,本文提出的计算方法不仅能够精确地计算风电场的短路电流的初值与稳态值,还能较准确地描述风电场短路电流的变化规律。
分别在不同双馈风力发电机组和永磁风力发电机组容量比下(双馈风力发电机组与永磁风力发电机组容量比为3∶1、2∶1、1∶1、1∶2、1∶3)、不同故障点位置(AB 线上距B 点20%、30%、40%、50%、60%、70%处)的条件下,进行了多组测试,获得如图9所示的短路电流计算结果与实测结果误差图。分别对比了故障后初始时刻、稳态时刻(故障后100 ms)以及动态过程中20 ms 和50 ms时的短路电流计算结果与实测结果的误差。由图9可知,本文提出的方法对不同故障下短路电流初值的计算误差小于4%,稳态值的计算误差小于3%,该误差能满足保护动作特性评估的要求;且在电流衰减过程中的计算误差小于6%,准确描述了短路电流的变化机理。
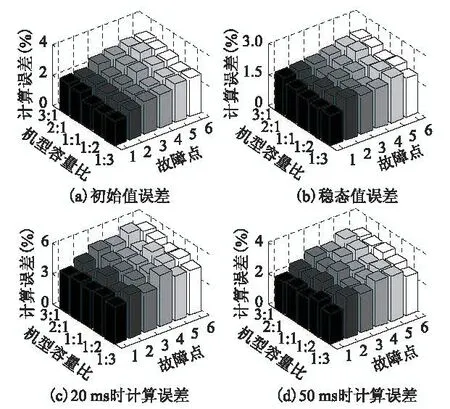
图9 短路电流实测结果与模型计算结果比较Fig.9 Comparison between calculation result and test result of the short circuit current
5 风电场接入的电网故障分析方法
当风电场采用低电压穿越控制模式,为系统电压提供支撑时,由式(12)、式(17)可知,故障稳态下双馈风力发电机组和永磁风力发电机组均输出持续的工频短路电流。其中,双馈风机可表示为电压源与阻抗串联的形式,永磁风力发电机组可表示为电流源形式。因此,故障稳态时可建立如图5所示的风电场简化等效电路,并与网侧电路联立,建立节点电压方程,进行故障分析。
当系统发生对称故障时,双馈风力发电机组和永磁风力发电机组只存在正序的电压源、电流源。对于不对称故障,风力发电机组锁相环可快速、准确地锁定正序电压的相位,并获得正序电压幅值,从而可根据式(11)、式(13)得到无功电流参考值和相应的有功电流参考值。通过调节变流器电流内环的PI 环节使短路电流的d、q 轴分量迅速跟踪上有功、无功电流参考值,可近似忽略其暂态过程。因此,不对称故障时,短路电流的表达式与式(11)、式(13)相同。由上述分析可知,系统发生对称、不对称故障时,双馈风力发电机组和永磁风力发电机组在故障稳态只存在正序的电压源、电流源。由式(12)、式(17)可知,双馈风力发电机组和永磁风力发电机组稳态电压源、电流源可分别表示为
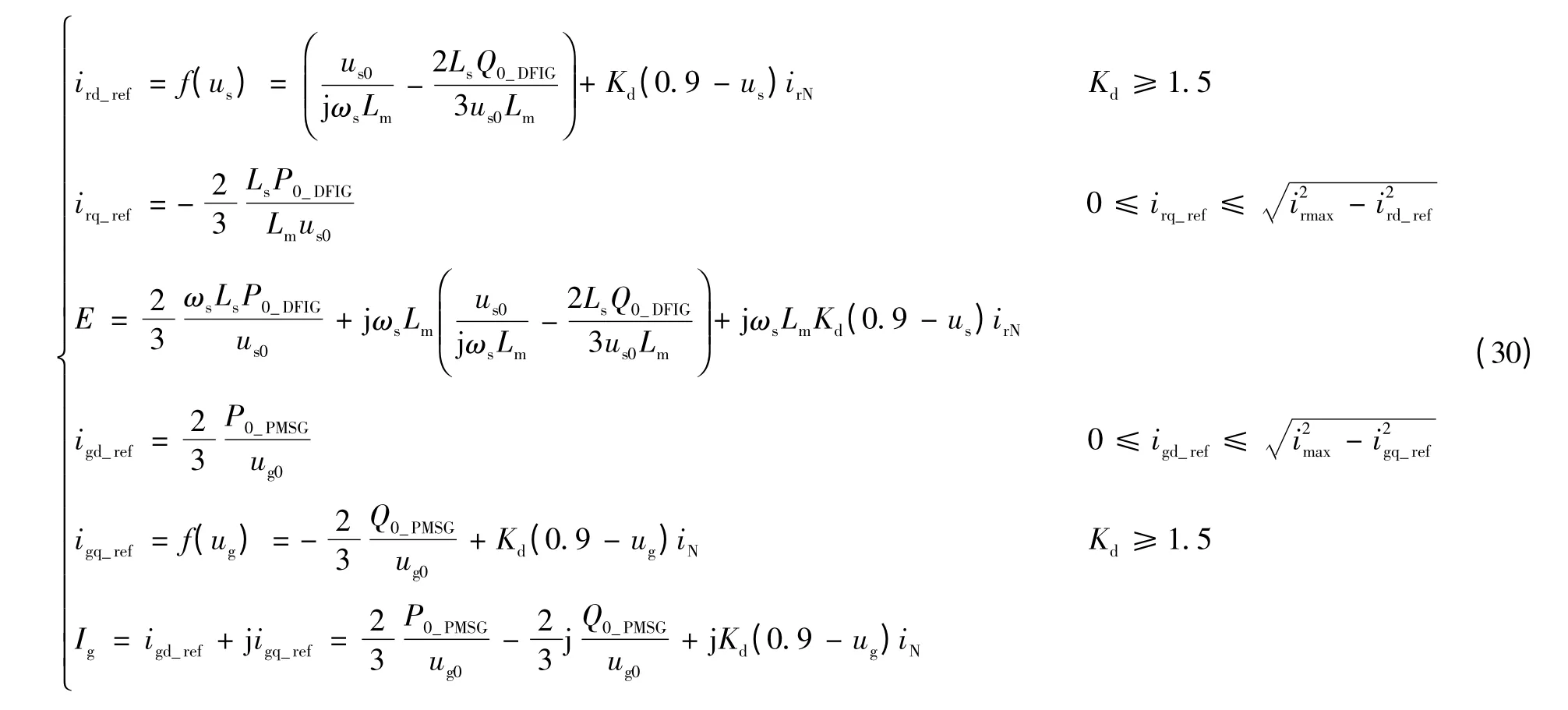
以图3所示的并网混合型风电场为例对风电场接入后的电网故障分析方法进行研究。假设在B 点发生AB 相接地短路,其正、负序网络如图10所示。EL、ZL分别为系统等效电势、阻抗;Z1L为系统到短路点的等效阻抗;Z2L为风电场到短路点的等效阻抗;Zf为过渡电阻。
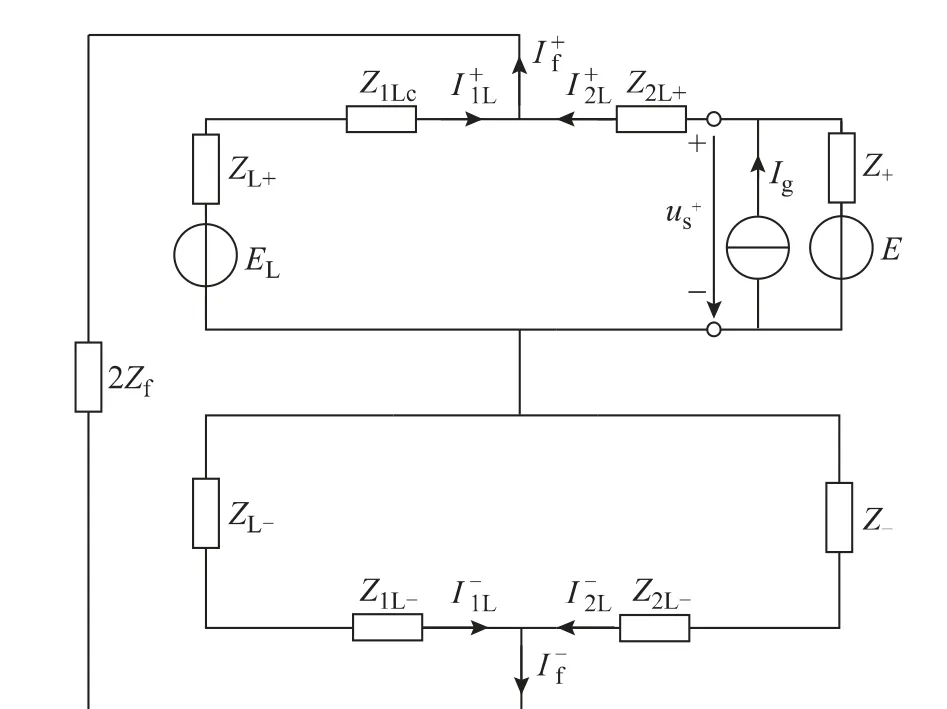
图10 风电场接入的电网序网络图Fig.10 Sequence networks of grid with wind farm
由于,简化风场模型中双馈风力发电机组和永磁风力发电机组均并接于集电母线,即双馈风力发电机组和永磁风力发电机组机端us=ug。则根据基尔霍夫电压、电流定律,由图10可得

AB 相短路的边界条件为
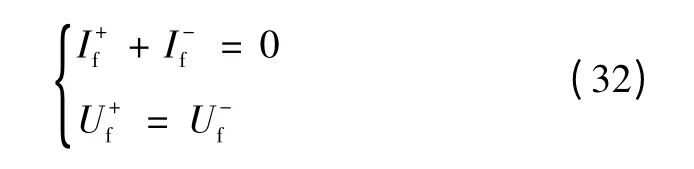
联立式(30)~式(32)即可求得AB 相接地短路时,各节点的电压和支路电流。同样的,可通过计算获得其他类型故障时电网各节点的电压与支路电流。
构建如图3所示的电网模型,对上述含混和型风电场接入的电网故障分析方法进行验证。表1 为额定工况下,在B 点发生三相短路时各支路短路电流的实验测试值与模型计算值的对比。表2 为额定工况下,在B 点发生AB 相接地短路时各支路短路电流正、负序分量的实验测试值与模型计算值对比。
由表1 和表2 可知,在对称和不对称短路情况下,本文提出故障分析方法的计算结果与实验测试结果非常接近,而等效同步发电机的传统方法误差较大。由于实验选取的风场规模小,其输出的短路电流有限,传统故障分析方法尚可粗略计算。若风电场大规模集中接入,其输出电流可能超过系统侧提供的短路电流,此时采用不考虑风电场暂态特性的传统分析方法,将会产生更大的计算误差。
实验验证了采用本文所提的风电场等效模型,能够正确地计算短路电流的幅值与相位。基于该模型建立的含风电场接入的电网故障方法,能有效提高计算准确度,正确分析风电场接入的影响。
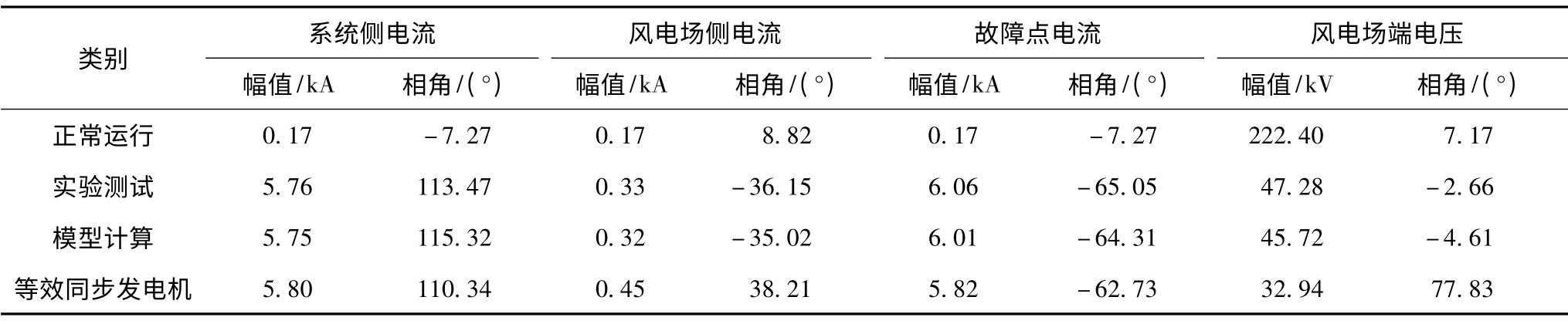
表1 三相短路时模型计算值与实验测试值比较Tab.1 Comparison between simulation calculation result and experimental test result three-phase short circuit
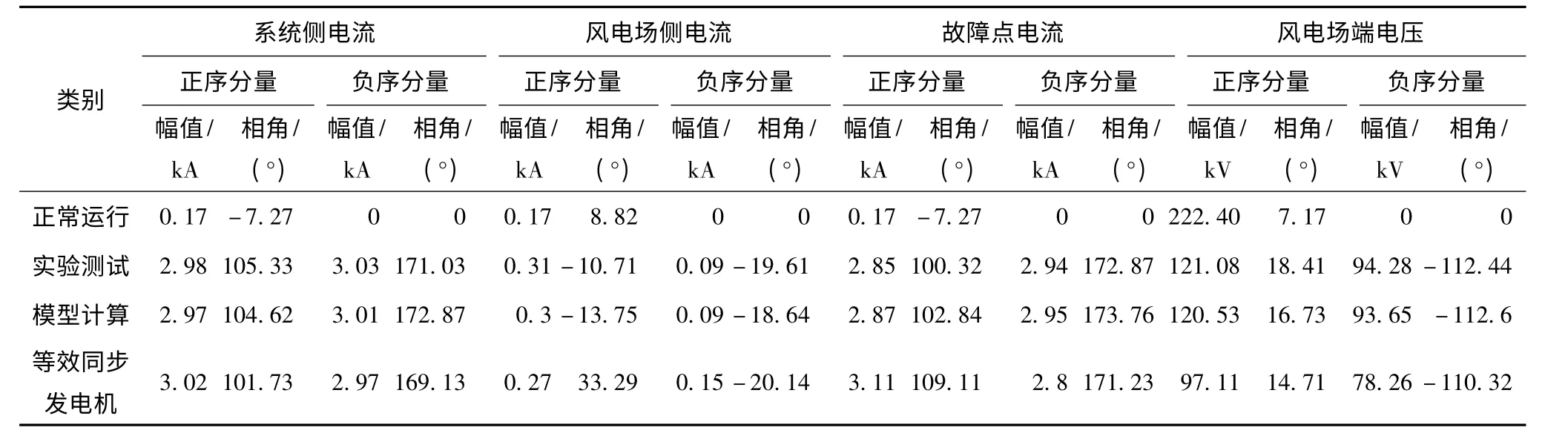
表2 AB 两相短路时模型计算值与实验测试值比较Tab.2 Comparison between simulation calculation result and experimental test result AB two-phase short circuit
6 结论
针对大规模风电场故障分析中风力发电机组类型多样、现有模型无法等效风电场的故障暂态过程等问题,本文考虑了低电压穿越控制策略的影响,建立了双馈风力发电机组与永磁风力发电机组的单机等效模型。并在分析故障期间短路电流变化机理的基础上,采用分群聚合等效,提出了风电场的短路电流计算方法。并在此基础上对含风电场接入的电网故障分析方法进行了探讨与分析。RTDS 实验平台的测试结果表明:
1)分析了低电压穿越控制策略对风力发电机组暂态过程的影响机理,根据我国新的风电并网标准的要求,建立了故障期间双馈风力发电机组与永磁风力发电机组的等效模型,准确描述了各类风力发电机组的暂态过程。
2)经实验验证本文所提的风电场短路电流计算方法不仅能准确计算风电场的短路电流的初值与稳态值,还能较准确地描述短路电流的变化规律。
3)针对故障稳态时双馈风力发电机组和永磁风力发电机组等效电路的特性,提出了适用于风电场接入的电网故障分析方法,准确计算了风电场接入后的电网在对称及不对称故障下各支路中的短路电流。
[1] 王振树,刘岩,雷鸣,等.基于Crowbar 的双馈机组风电场等效模型与并网仿真分析[J].电工技术学报,2015,30(4):44-51.
Wang Zhenshu,Liu Yan,Lei Ming,et al.Doubly-fed induction generator wind farm aggregated model based on Crowbar and integration simulation analysis[J].Transactions of China Electrotechnical Society,2015,30(4):45-51.
[2] 苏勋文,徐殿国,卜树坡.风速波动下风电场变参数等效建模方法[J].电工技术学报,2013,28(3):277-284.
Su Xunwen,Xu Dianguo,Bu Shupo.Variable parameter equivalent modeling method of wind farms under wind speed fluctuations[J].Transactions of China Electrotechnical Society,2013,28(3):277-284.
[3] Conroy J,Watson R.Aggregate modeling of wind farms containing full converter wind turbine generators with permanent magnet synchronous machines:transient stability studies[J].IET Renewable Power Generation,2008,3(1):39-52.
[4] Fernandez L M,Garcia C A,Saenz J R,et al.Equivalent models of wind farms by using aggregated wind turbines and equivalent winds[J].Energy conversion and management,2009,50(3):691-704.
[5] 米增强,苏勋文,杨奇逊,等.风电场动态等效模型的多机表征方法[J].电工技术学报,2010,25(5):162-169.
Mi Zengqiang,Su Xunwen,Yang Qixun,et al.Multimachine representation method for dynamic equivalent model of wind farms[J].Transactions of China Electrotechnical Society,2010,25(5):162-169.
[6] 周海强,张明山,薛禹胜,等.基于戴维南电路的双馈风电场动态等效方法[J].电力系统自动化,2012,36(23):42-46.
Zhou Haiqiang,Zhang Mingshan,Xue Yusheng,et al.A dynamic equivalent method for doubly-fed induction generator wind farm based on Thevenin equivalent circuit[J].Automation of Electric Power Systems,2012,36(23):42-46.
[7] 乔嘉赓,鲁宗相,闵勇,等.风电场并网的新型实用等效方法[J].电工技术学报,2009,24(4):209-213.
Qiao Jiageng,Lu Zongxiang,Min Yong,et al.New dynamic equivalence method for grid-connected wind farm[J].Transactions of China Electrotechnical Society,2009,24(4):209-213.
[8] 曹娜,于群.风速波动情况下并网风电场内风电机组分群方法[J].电力系统自动化,2012,36(2):42-46.
Cao Na,Yu Qun.A grouping method for wind turbines in agridconnected wind farm during wind speed fluctuation[J].Automation of Electric Power Systems,2012,36(2):42-46.
[9] 苏常胜,李凤婷,武宇平.双馈风电机组短路特性及对保护整定的影响[J].电力系统自动化,2011,35(6):86-91.
Su Changsheng,Li Fengting,Wu Yuping.An analysis on short-circuit characteristic of wind turbine driven doubly fed induction generator and its impact on relay setting[J].Automation of Electric Power Systems,2011,35(6):86-91.
[10] 全国电力监管标准化技术委员会.GBT_19963-2011风电场接入电力系统技术规定[S].北京:中国标准出版社,2011.
[11] 张保会,张金华,原博,等.风电接入对继电保护的影响(六)——风电场送出线路距离保护影响分析[J].电力自动化设备,2013,33(6):1-6.
Zhang Baohui,Zhang Jinhua,Yuan Bo,et al.Impact of wind farm integration on relay protection(6):analysis ofdistance protection for wind farm outgoing transmission line[J].Electric Power Automation Equipment,2013,33(6):1-6.
[12] Fernández L M,Jurado F,Saenz J R.Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines[J].Renewable Energy,2008,33(1):129-140.
[13] 陈树勇,王聪,申洪,等.基于聚类算法的风电场动态等效[J].中国电机工程学报,2012,32(4):11-19.
Chen Shuyong,Wang Cong,Shen Hong,et al.Dynamic equivalence for wind farms based on clustering algorithm[J].Proceedings of the CSEE,2012,32(4):11-19.
[14] Kanellos F D,Kabouris J.Wind farms modeling for short-circuit level calculations in large power systems[J].IEEE Transactions on Power Delivery,2009,24(3):1687-1695.
[15] 撖奥洋,张哲,尹项根,等.双馈风力发电系统故障特性及保护方案构建[J].电工技术学报,2012,27(4):233-239.
Han Aoyang,Zhang Zhe,Yin Xianggen,et al.Research on fault characteristic and grid connecting-point protection scheme for wind power generation with doublyfed induction generator[J].Transactions of China Electrotechnical Society,2012,27(4):233-239.

