基于可信理论的多目标模糊机会约束无功优化

刘文学 梁 军 贠志皓 牛 睿 褚壮壮

(1.山东大学电网智能化调度与控制教育部重点实验室 济南 250061 2.国网南京供电公司 南京 210019)

0 引言

电力系统无功优化是指在电网结构参数、系统负荷、发电机有功出力给定的情况下，通过合理调整发电机机端电压、电压器分接头和无功补偿设备的投切，在满足系统约束的前提下，使电网安全经济运行水平达到最优。无功优化能够改变系统潮流分布，加强电网安全稳定，提高电压质量，对保证电网安全经济可靠的运行具有重要作用。电力系统运行水平和要求的提高，使得无功优化已经表示为一个多约束、非线性的多目标优化模型［1-6］。

受各种因素影响，电网中包含不确定性的参数和数据，许多研究考虑了其对无功优化的影响［7-12］。文献［7］运用双层优化原理提出一种分析不确定负荷对电网无功优化影响的模型。面对复杂多变的电力系统，这种仅考虑单个节点不确定负荷的方法缺乏灵活性。文献［8］从风险的角度分析有功损耗、电压失稳以及电压越限给电力系统运行造成的影响，但风险损失的确定具有大量的主观性。配电网中无功优化仅考虑风机机组对配电网的影响，无法考虑对大规模风电场并入输电系统的影响［9-12］。文献［13］建立了考虑风电功率概率的随机期望无功优化模型，并利用蒙特卡洛模拟和贪心算法给予解决，对不确定条件下的无功优化模型具有启发性。

然而，由于受到位置、温度、天气等环境的影响，间歇性电源出力和负荷往往具有模糊性，采用模糊参数的表达方式较为合适［14］。文献［15］考虑了电力系统模糊因素的存在，建立了多目标模糊无功优化模型，使用函数联接网络确定及细调隶属函数，并采用遗传算法搜索全局最优解。文献［16］建立梯形模糊数表示分布式电源出力的无功电压优化模型，利用其隶属度函数形成模糊适应度函数，并采用遗传算法给予解决。以上文献都是利用模糊理论中的可能性测度，不能判断事件发生的可信程度，所得优化结果在实际中存在一定风险，而且无法量化风险，因此有必要将可信理论引入模糊无功优化模型。可信性测度是模糊变量中的重要概念，具有自对偶性和次可加性，能够判断事件是否一定发生［17］，能够弥补隶可能性测度表达风险的不足，已经广泛地应用在电力系统中，如模糊潮流［18］、检修计划［19］、风险评估［20］、输电网规划［21］、动态经济调度［22］和机组组合［23］等。

本文利用梯形模糊数表示间歇性电源出力和负荷，并结合可信性理论和模糊机会约束规划，用置信水平控制风险，建立多目标模糊无功优化模型。为求解该模型，本文提出新的可信性模糊潮流计算方法减少模糊模拟的计算时间，利用交互满意度将多目标优化转换为单目标优化而获得Pareto 解，引入蝙蝠算法提高优化准确度和效率。算例结果表明所提模型和算法的可行性和有效性。

1 电力系统多目标模糊机会约束无功优化

1.1 可信性理论

模糊数学中有可能性测度、必要性测度和可信性测度3 类。可信性测度具有自对偶性和次可加性，是与概率论中概率测度并行的概念。若该事件的可信性为1，则必然成立，反之，若可信性为0，则必不成立。

对于可能性空间(Θ，P(Θ)，Pos)，可信性测度表示为［17］

式中:Pos{A}为事件A 的可能性测度;Nes{A}为事件A 的必要性测度。

可信性分布Φ(x)表示模糊变量ξ 取值小于或等于x 可信性，Φ(x)为

乐观值和悲观值是常用来度量模糊变量的两个指标，其定义如下:

定义1 假设ξ 为模糊变量，且β ∈(0，1］，则

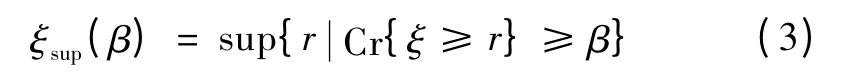
式中:ξsup(β)为ξ 的β 乐观值，ξsup(β)是模糊变量ξ 以可信性β 所取值中最大的值;sup 表示上确界，即最小上界。

定义2 假设ξ 为模糊变量，且β ∈(0，1］，则

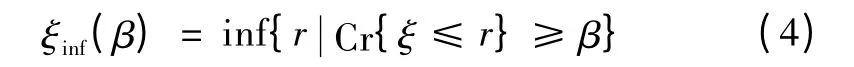
式中:ξinf(β)为ξ 的β 悲观值，ξinf(β)是模糊变量ξ 以可信性β 所取值中最小的值;inf 表示下确界，即最大下界。

1.2 基于可信性的的机会约束模型

模糊机会约束规划包括minimax 机会约束规划模型和minimin 机会约束规划模型［17］。minimax 机会约束规划在约束条件下以一定的置信水平成立，极小化目标函数的乐观值。minimin 机会约束规划在约束条件下以一定的置信水平成立，极小化目标函数的悲观值。minimax 机会约束规划模型为

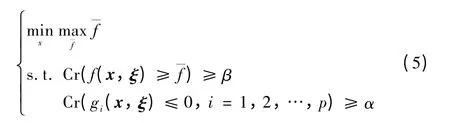
式中:x 为决策向量;ξ 为模糊向量，ξ=(ξ1，ξ2，…，ξn);gi(x，ξ)为约束函数;p 为约束函数的数量;f(x，ξ)为目标函数;是目标函数f(x，ξ)的β 乐观值。α 和β分别为决策者预先给定的置信水平。模糊向量使得约束函数的计算结果变成模糊变量其范围不能用确定条件下的不等式描述，而用可信测度下的机会约束处理，如式中所示。目标函数的计算结果也为模糊变量，不能给出一个确定的目标值，因此用目标函数的β 乐观值作为优化目标。因此，minimax 模型的评价指标为β 乐观值fmin。

minimin 机会约束规划模型为

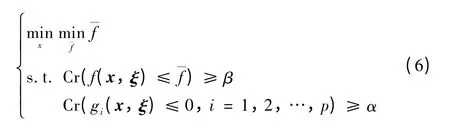
式中min—f为目标函数f(x，ξ)的β 悲观值。同minimax模型类似，minimin 模型的评价指标为β 悲观值fmax。

显然，minimax 模型和minimin 模型是两种极端情况，可以通过赋予这两种情形不同的权重λ 和1 － λ，给出极端乐观和极端悲观的折中方案，即fcom=λfmin+(1 － λ)fmax。因此机会约束规划模型定义为

式中λ 为乐观程度，当λ=0时，目标极端悲观;当λ=1时，目标极端乐观。

1.3 多目标无功优化的模糊机会约束模型

电网中的参数为模糊变量时，电网中的状态变量(如节点电压、发电机无功出力、和线路传输功率)和目标函数(如系统网络损耗、电压偏移)都为模糊变量，而且其可信性分布受控制变量和模糊变量隶属度函数决定。本文以系统网损与电压偏移的折中值为优化目标，其中控制变量为发电机节点电压、变压器变比和并联电容器补偿容量，建立多目标无功优化机会约束规划模型。

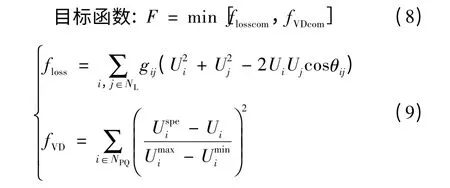
约束条件:

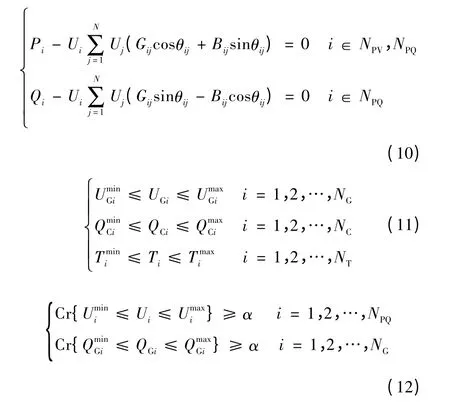
式中:floss和fVD分别为系统网损和电压偏移;flosscom、fVDcom分别为系统网损和电压偏移在置信水平至少β时所取得折中值;N、NG、NC、NT分别为系统节点数量、发电机数量、补偿电容器数量、可调变压器数量;NL、NPV、NPQ分别为输电线路集合、PV 节点集合、PQ 节点集合;gij、θij为节点i 与j 之间的线路电导、电压相角差;分别为节点的电压幅值、电压基准值、下限和上限。式(10)为潮流平衡方程，式中Pi和Qi分别为节点有功功率和无功功率注入量的预测值;Gij与Bij分别为导纳矩阵的第i 行j列的实部和虚部。式(11)为决策变量的不等式约束，式中UG6i、QCi、Ti分别为发电机机端电压、补偿电容器容量和可变电压器变比，、分别对应控制变量的上下限。式(12)为状态变量的机会约束，分别为节点i 发电机无功出力的下限和上限。

2 多目标模糊机会约束无功优化的求解

2.1 基于可信性的模糊潮流

梯形隶属度函数由于具有丰富的理论基础，而且现实中符合对事物的判断，被广泛地应用在电力系统中［15，16］。间歇性电源和负荷的不确定性出力的梯形隶属度函数由预测值和四元比例参数表示为

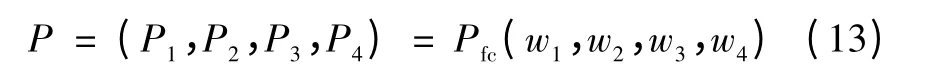
式中:Pfc为预测值;wk为比例系数，k=1，2，3，4。

模糊机会约束无功优化模型的目标函数和约束中存在可信性的求解。如何通过模糊潮流求解可信性机会约束是求解模糊机会约束优化模型的关键，文献［18］提出利用模糊模拟求解基于可信性的模糊潮流，但该方法计算量大，计算周期较长，不适用于模糊无功优化模型，可以作为其他可信性的模糊潮流算法的标准测试工具。

可信性测度是在模糊变量隶属度函数基础上推导出的测度，本文提出一种通过隶属度函数来解状态变量可信分布的方法，其具体求解步骤如下:

1)不考虑间歇性电源的无功调节能力，将间歇性电源视为PQ 节点。间歇性电源无功出力Qin为

式中:Pin为间歇性电源有功出力;φ 为功率因数角。

2)由间歇性电源出力和负荷的预测值求解确定性交流潮流方程，得到系统节点电压幅值、节点电压相角、PV 节点发电机无功出力、网路损耗和电压偏移确定值Vd、θd、Qd、Plossd、VVDd，下标d 表示对应变量的确定值。

3)求包括间歇性电源出力和负荷在内各个节点注入功率的模糊增量ΔP、ΔQ。

4)求节点电压及相角的模糊增量ΔV、Δθ。本文研究的系统满足P-Q 解耦特性，可以利用快速解耦潮流算法求解

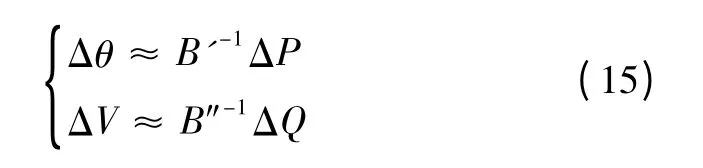
5)求解节点电压及相角模糊变量V、θ。

6)求解发电机无功出力、网路损耗和电压偏移模糊变量。

在对应预测值的运行点附近线性化式，通过泰勒级数展开

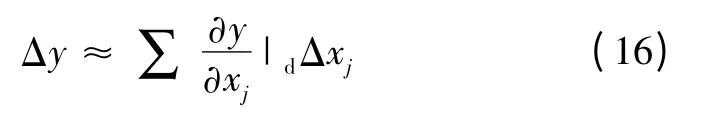
式中:y 为发电机无功出力、网路损耗和电压偏移，其计算如式(9)所示;xj为与y 直接相关的系统模糊变量，如节点电压及相角。状态变量的模糊增量已知后，由式(17)便可求目标函数的隶属度函数

7)通过隶属度函数和式(1)求解状态模糊变量及目标函数模糊变量的可信性分布。

2.2 多目标处理策略

Pareto 解是多目标优化的重要概念，Pareto 最优前沿是可行域内的最优解集。但是Pareto 最优前沿的获得需要很大的计算量，而且实际需求中还需要根据决策者的经验或需求进一步选择单个最优解。因而，本文采用模糊决策将多目标优化转换为单目标优化。当采用模糊规划的方法求解多目标决策问题时，需要重点解决两个问题:①选择适当的隶属度函数来刻画模糊目标;②采用某个模糊算子对不同的目标进行综合，以形成整体满意度，使所求解为Pareto 解。

决策者引入隶属函数的具体方法如下:

首先计算

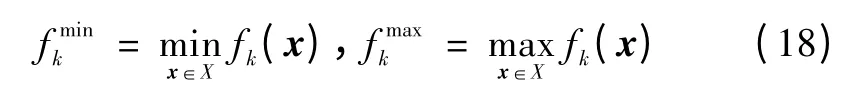
式中:k=1，2，…，K，K 为优化目标数量;X 为优化的可行域;x 为决策向量分别为可行域内第k个优化目标的最小值和最大值。本文选择线性函数构造隶属度函数［24］。

选好目标函数隶属度函数后，决策者需要构造模糊决策算子进行对多目标综合评价。交互满意法从极小极大演化而来的模糊算子，既能够避免决策时需要目标模糊函数0 ＜μk(fk(x))＜1 的条件，又能验证所求结果的有效性。

交互满意法的步骤如下［24］:

1)决策者已经根据主观偏好确定各目标函数fk(x)的隶属度函数μk(fk(x))，并给出参考隶属值。

2)为了避免进行解的有效性检验，只考虑求解以下扩展的极小极大问题。

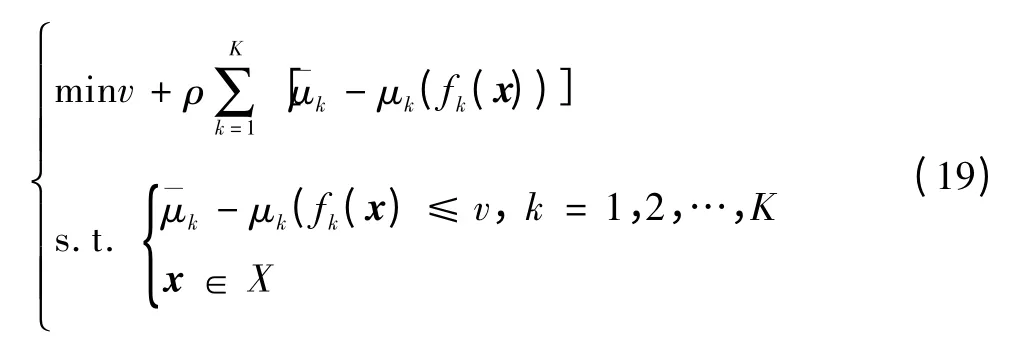
式中ρ 为充分小的正数，可以取［10－3，10－5］。

3)求解扩展的极小极大问题只是用来产生决策者的局部满意解。如决策者对当前的解不满意，则需要通过改变参考隶属值求得新的满意解。

2.3 蝙蝠算法

蝙蝠算法(Bat Algorithm，BA)是由剑桥大学的杨新社提出的搜索全局最优的启发式群体智能优化算法。该算法以回音定位的声学原理为基础，通过模拟捕食行为寻求优化问题的最优解［25］。文献［25］指出在很多测试函数中，蝙蝠算法在计算精度和效率上优于遗传算法和粒子群算法。因此，将蝙蝠算法引入本文提出的无功优化模型。

优化过程主要由蝙蝠利用超声波特征捕捉食物的机制获得，其原理如下:①蝙蝠个体之间以固定最小频率通过相互比较使处于适应度值较劣的个体不断向空间位置较优的个体移动，局部搜索中按照随机游走法则产生局部新解;②音量与脉冲发生率影响蝙蝠个体寻找食物的速度和准确度，迭代刚开始采用较强的音量和较小的脉冲发生率，一旦捕捉到食物(当前最优解)，则减少音量，增大脉冲发生率。蝙蝠算法就是将蝙蝠个体作为问题求解空间分布点，将问题寻优过程转化为蝙蝠个体捕捉食物和位置更新的过程，将目标函数适应度值的好坏转化为蝙蝠所处空间的优劣。每一次迭代，蝙蝠个体位置不断更新，问题的求解得到优化。

对原理1 进行模拟仿真，蝙蝠个体更新速度和位置的公式为

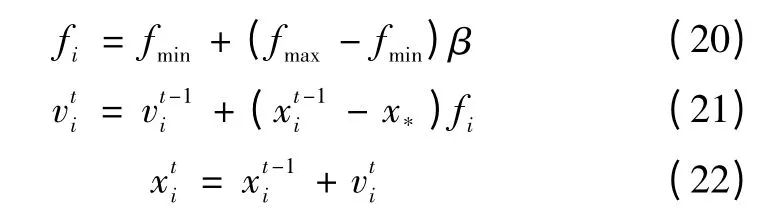
式中:fi为频率;［fminfmax］为频率区间;β 为服从均匀分布的随机变量分别为第i 维t 迭代的蝙蝠种群的位置和速度;x*为当前全局最优解。

对于局部搜索，每只蝙蝠按照随机游走法则产生局部新解

式中:ε 为一个随机数，ε ∈［－ 1，1］;At为当前迭代所有蝙蝠的平均音量。

根据原理2，音量和脉冲发生率的更新公式为

2.4 算法流程

求解多目标模糊机会约束无功优化的流程如下:

1)输入电力系统原始数据，包括电力系统线路，节点发电机出力，间歇性电源出力和负荷的模糊参数，发电机端电压、变压器和投切电容器的范围。

2)输入BA 算法的控制参数，并设定t=0、最大迭代次数T 和种群规模n。

4)通过可信性的模糊潮流计算蝙蝠种群中个体位置目标函数和状态变量可信性分布，并将目标函数表示为隶属度值，通过交互满意法得到蝙蝠个体的极小化目标值，利用罚函数方式处理机会约束，并得到蝙蝠个体位置的适应度。

5)对每个蝙蝠个体通过调整频率按照式(21)和式(22)更新蝙蝠个体的速度和位置，产生新解。

8)重排蝙蝠个体，并找到当前最优值。

9)判断最大迭代次数。t=t+1，若t=T，则结束，输出最优个体;否则转到步骤4)。

3 算例分析

3.1 基本数据与参数

本文选取IEEE30 节点标准系统，其线路参数不变。在11、23 节点由火电机组换成风电场，有功出力预测值分别为38 MW 和27 MW。22 节点并入光伏发电站，有功出力预测值为23.5 MW。风电场和光伏发电站的功率因数都为0.98。有功负荷都为标准系统的1.5 倍，无功负荷都为标准系统的1.7 倍。控制变量包括4 台发电机节点电压、4 台可调变压器变比和2 组并联补偿电容器容量。负荷和风电、光伏出力采用梯形模糊数表示，模糊隶属度比例系数见表1，目标函数乐观程度为0.5。本文选自MATLAB 编程求解，最大迭代次数为100，种群数为50，重复运算20 次，其他算法参数见文献［25］。目标函数的参考隶属度都选择1。

表1 梯形模糊参数Tab.1 Trapezoidal fuzzy parameters

3.2 计算结果分析

由于本文所提模糊潮流方法在求解可信度时进行线性近似，为了验证方法的有效性，需要和测试标准(文献［18］所提方法)做对比。图1为未经优化控制变量条件下，两种方法的电网有功网损可信度分布曲线。从图中可以看出，本文算法的结果与模糊模拟仿真得到的的曲线极其相似，可以作为模糊潮流的近似计算方法。为了进一步说明本文模糊潮流求解可信度的优越性，对两种方法进行时间计算比较，本文方法计算时间为0.021 s，传统模糊模拟方法为198.75 s。而本文提出的无功优化模型在优化过程中需要计算大量的模糊潮流，因此更适合采用本文提出的模糊潮流方法计算系统的可信度。

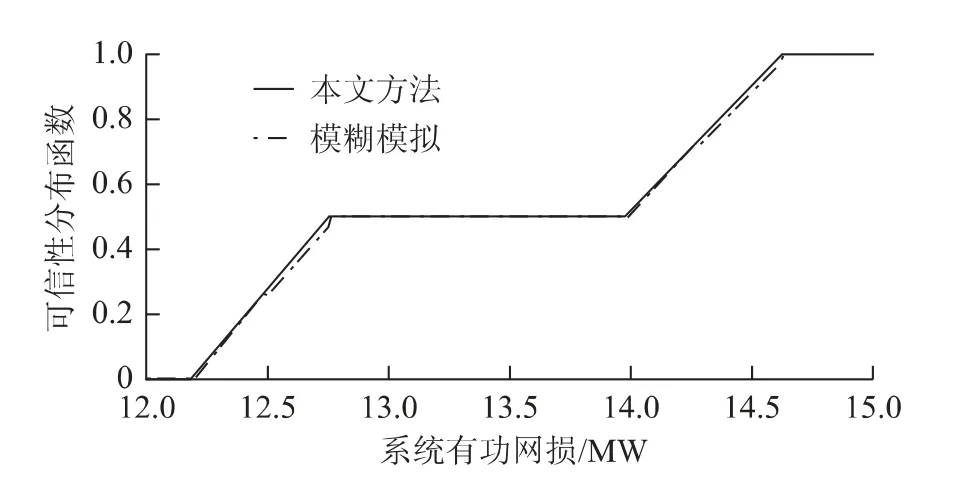
图1 系统有功网损的可信性分布函数比较Fig.1 Comparison of credibility distribution function of active power loss of system

为了说明本文研究间歇性电源和负荷的模糊性对无功优化的影响，将不考虑不确定条件下的常规多目标优化与本文所提模型进行对比，如表2 所示。从表中可以看出:网络损耗方面，本文模型在乐观值和悲观值上都优于常规模型;电压偏移方面，本文模型在悲观值上优于常规模型。图2显示了两种模型目标函数的可能性(隶属度函数)，从图中可看出，本文模型更适合不确定性的环境。

表2 不同模型结果的对比Tab.2 Comparison of different model results

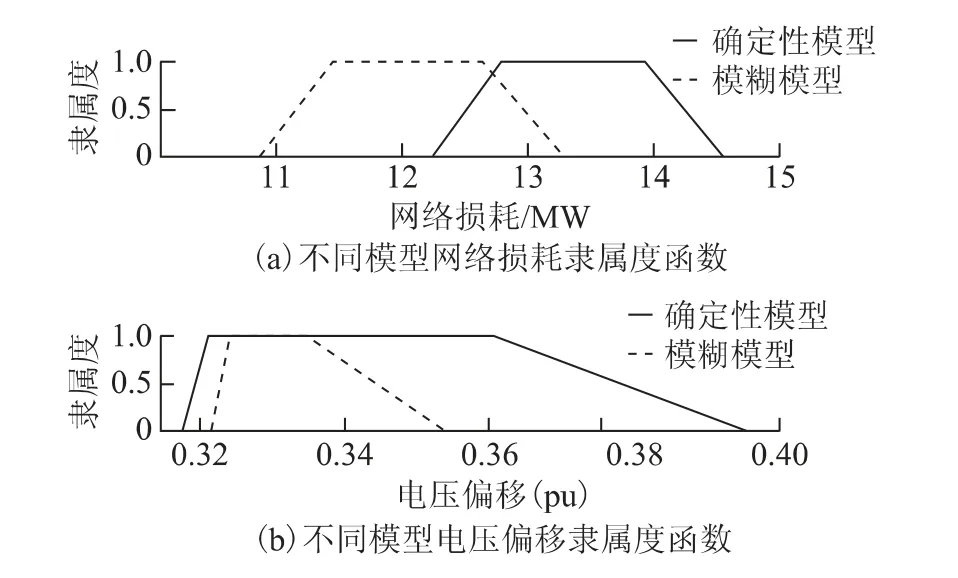
图2 不同模型隶属度函数的比较Fig.2 Comparison of membership function of different model

模糊置信水平对电网优化结果有着重要的影响，本文分析目标函数和约束条件不同模糊置信水平下对无功优化的影响。图3为目标函数约束为100%的条件下，不同约束模糊置信水平的网络损失和电压偏移的折中值。从图中可以看出:随着约束条件的模糊置信水平提高，系统的两个目标函数的优化值也在提高，说明约束条件模糊置信水平反映了不确定条件下的风险。实际决策时要根据数据分析，选择适当的模糊置信水平，既能满足风险约束，又能优化电网的网络损耗和电压偏移。

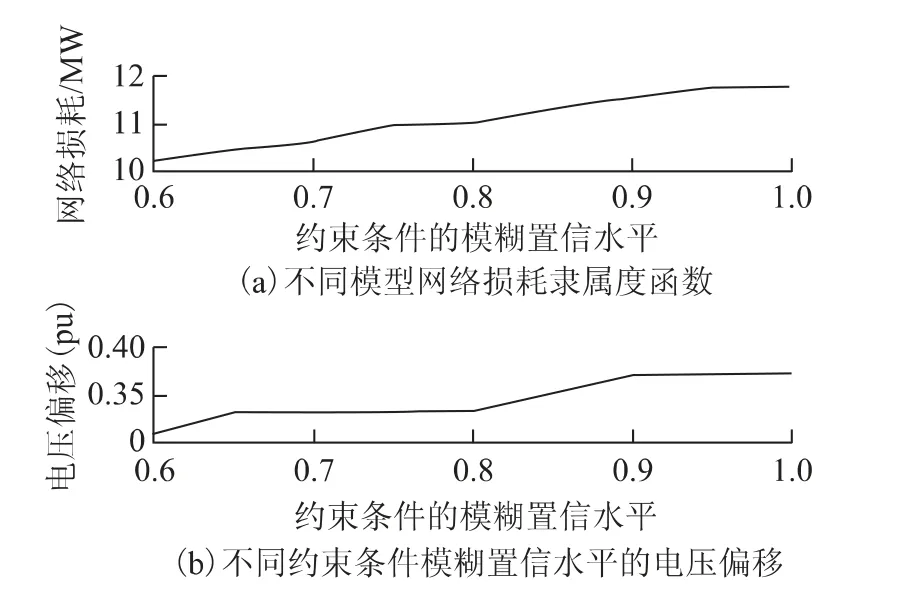
图3 不同约束条件模糊置信水平下的网络损耗和电压偏移Fig.3 The network real power loss and the total voltage deviation under different constraints fuzzy confidence levels

表3 为约束可信水平为100%，不同目标函数可信程度下的有功网损和电压偏移。由表可知:随着目标函数置信水平的增大，电网损耗的模糊参数增大，而电压偏移的模糊参数减少。说明目标函数置信水平的提高，目标函数中更侧重于网络损耗的优化。

表3 不同目标函数置信水平的模糊参数Tab.3 Fuzzy parameters under different objective fuzzy confidence levels

在目标函数和约束条件模糊置信水平为100%的情况下，蝙蝠算法、遗传算法(Genetic Algorithm，GA)和粒子群算法(Particle Swarm Optimization，PSO)的最优值迭代过程中如图4所示。多目标优化的直接结果如表4 所示，从表中可看出在网络损耗与电压偏移两个目标上，蝙蝠算法都占有优势，验证了图4的收敛结果。通过图4可看出，在收敛速度方面，粒子群算法与蝙蝠算法接近，但粒子群算法易陷入最优值;蝙蝠算法在算法寻优精度和收敛速度优于遗传算法，表明了蝙蝠算法同样适合本文提出的无功优化模型。从蝙蝠算法的思想和实现来看，BA 是个非常有前途的算法，性能上超过粒子群算法和遗传算法，其主要原因是BA 结合了这些算法的优点。

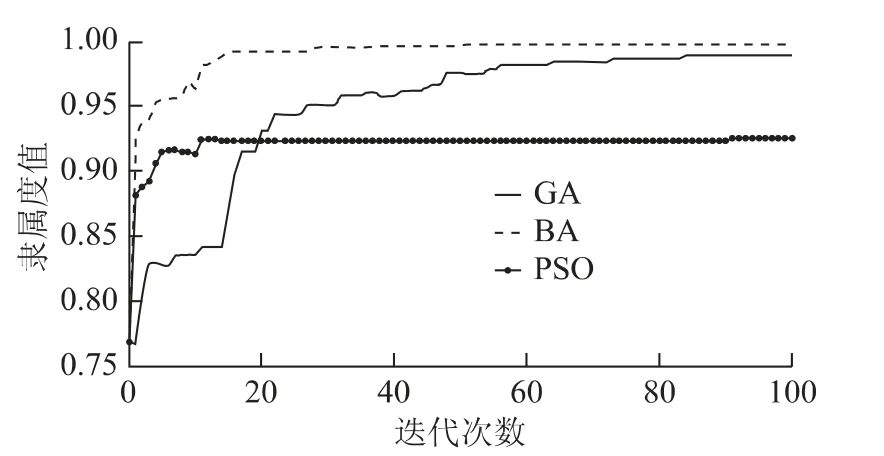
图4 算法的收敛特性曲线Fig.4 The curve of convergence characteristic of methods

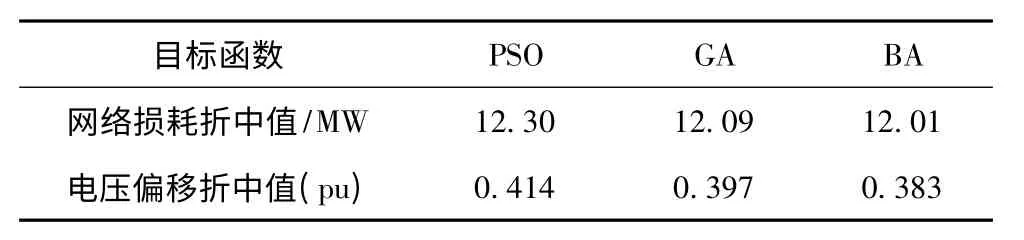
表4 不同算法的计算结果Tab.4 Results of different algorithms

4 结论

针对电力系统的不确定因素，如间歇性电源出力的间歇性和波动性及负荷预测的模糊性，本文将可信性理论引入电力系统多目标无功优化模型中，提出了新的模糊潮流计算方法求解中的可信性约束，并利用模糊规划中的交互满意度将多目标转换为单目标优化，利用新兴的蝙蝠算法给予求解，得到给定可信度下的无功优化控制方案。

算例分析表明提出的模糊潮流计算方法的适应性，模糊置信水平的选择对无功优化方案有着重要的影响。目标函数的模糊置信水平越高，优化方案越倾向于网络损耗。约束条件的模糊置信水平越高，系统的安全风险越低，而优化目标就越大。蝙蝠算法在寻优精度和收敛速度上都优于传统的遗传算法和粒子群算法。

［1］ 程军照，李澍森，程强．一种无功优化预测校正内点算法［J］．电工技术学报，2010，25(2):152-157．

Cheng Junzhao，Li Shusen，Cheng Qiang．A predictorcorrector interior point method for optimal reactive power［J］．Transactions of China Electrotechnical Society，2010，25(2):152-157．

［2］ 李鑫滨，朱庆军．一种改进粒子群优化算法在多目标无功优化中的应用［J］．电工技术学报，2010，25(7):137-143．

Li Xinbin，Zhu Qingjun．Application of improved particle swarm optimization algorithm to multi-objective reactive power optimization［J］．Transactions of China Electrotechnical Society，2010，25(7):137-143．

［3］ EL-Dib A A，Youssef H K M，EL-Metwally M M，et al．Optimum VAR sizing and allocation using particle swarm optimization［J］．Electric Power Systems Research，2007，77(8):965-972．

［4］ 李智欢，段献忠．多目标进化算法求解无功优化问题的对比分析［J］．中国电机工程学报，2010，30(10):57-65．

Li Zhihuan，Duan Xianzhong．Comparison and analysis of multio-bjective evolutionary algorithm for reactive power optimization［J］．Proceedings of the CSEE，2010，30(10):57-65．

［5］ Liu X，Xu W．Economic load dispatch constrained by wind power availability:a here-and-now approach［J］．IEEE Transactions on Sustainable Energy，2010，1(1):2-9．

［6］ 李鸿鑫，李银红，陈金富，等．自适应选择进化算法的多目标无功优化方法［J］．中国电机工程学报，2013，33(10):71-78．

Li Hongxin，Li Yinhong，Chen Jinfu，et al．Multiple evolutionary algorithms with adaptive selection strategies for multi-objective optimal reactive power flow［J］．Proceedings of the CSEE，2013，33(10):71-78．

［7］ 王函韵，胡骅，朱卫东，等．信息不确定对电网无功优化的影响［J］．中国电机工程学，2005，25(13):24-28．

Wang Hanyun，Hu Hua，Zhu Weidong，et al．The impact of parameter uncertainty on reactive souurce optimization［J］．Proceedings of the CSEE，2005，25(13):24-28．

［8］ 戴剑锋，周双喜，鲁宗相，等．基于风险的电力系统无功优化问题研究［J］．中国电机工程学报，2007，27(22):38-44．

Dai Jianfeng，Zhou Shuangxi，Lu Zongxiang，et al．Study on reactive power optimization based upon risk［J］．Proceedings of the CSEE，2007，27(22):38-44．

［9］ 赵晶晶，符杨，李东东．考虑双馈电机风电场无功调节能力的配电网无功优化［J］．电力系统自动化，2011，35(11):33-38．

Zhao Jingjing，Fu Yang，Li Dongdong．Reactive power optimization in distribution network considering reactive power regulation capability of DFIG wind farm［J］．Automation of Electric Power Systems，2011，35(11):33-38．

［10］ 何禹清，彭建春，毛丽林，等．含多个风电机组的配电网无功优化［J］．电力系统自动化，2010，34(19):37-41．He Yuqing，Peng Jianchun，Mao Lilin，et al．Reactive power optimization in distribution system with multiple wind power generators［J］．Automation of Electric Power Systems，2010，34(19):37-41．

［11］ Hong Yingyi，Luo Yifeng．Optimal VAR control considering wind farms using probabilistic load-flow and gray-based genetic algorithms［J］．Transactions Power Delivery，2009，24(3):1441-1449．

［12］ 王淳，高元海．基于概率统计的含间歇性分布式发电的配电网无功优化［J］．电网技术，2014，38(4):1032-1037．

Wang Chun，Gao Yuanhai．Probability statistics based reactive power optimization of distribution network containing intermittent distributed generations［J］．Power System Technology，2014，38(4):1032-1037．

［13］ Chen Peiyuan，Siano P，Bak-Jensen B，et al．Stochastic optimization of wind turbine power factor using stochastic model of wind power［J］．IEEE Transactions on Sustainable Energy，2009，1(1):19-29．

［14］ 熊虎，向铁元，陈红坤，等．含大规模间歇式电源的模糊机会约束机组组合研究［J］．中国电机工程学报，2013，33(13):36-44．

Xiong Hu，Xiang Tieyuan，Chen Hongkun，et al．Research of fuzzy chance constrained unit commitment containing large-scale intermittent power［J］．Proceedings of the CSEE，2013，33(13):36-44．

［15］ 宋军英，刘涤尘，陈允平．电力系统模糊无功优化的建模及算法［J］．电网技术，2001，25(3):22-25．

Song Junying，Liu Dichen，Chen Yunping．A fuzzy model and approach for power reactive power optimization［J］．Power System Technology，2001，25(3):22-25．

［16］ 余昆，曹一家，陈星莺，等．含分布式电源的地区电网无功电压优化［J］．电力系统自动化，2011，35(8):28-32．

Yu Kun，Cao Yijia，Chen Xingying，et al．Reactive power and voltage optimization of the district grid with distributed generators［J］．Automation of Electric Power Systems，2011，35(8):28-32．

［17］ 刘宝碇，彭锦．不确定理论教程［M］．北京:清华大学出版社，2005．

［18］ 汪皓，吴文传，张伯明，等．基于可信性理论的模糊潮流方法［J］．电力系统自动化，2007，31(17):21-25．

Wang Hao，Wu Wenchuan，Zhang Boming，et al．Fuzzy power flow based on credibility theory［J］．Automation of Electric Power Systems，2007，31(17):21-25．

［19］ 冯永青，吴文传，张伯明，等．基于可信性理论的输电网短期线路检修计划［J］．中国电机工程学报，2007，27(4):65-71．

Feng Yongqing，Wu Wenchuan，Zhang Boming，et al．Short-term transmission line maintenance scheduling based on credibility theory［J］．Proceeding of the CSEE，2007，27(4):65-71．

［20］ 冯永青，吴文传，张伯明，等．基于可信性理论的电力系统运行风险评估(三)应用于工程实践［J］．电力系统自动化，2006，30(3):11-16．

Feng Yongqing，Wu Wenchuan，Zhang Boming，et al．Power system operation risk assessment based on credibility theory part three engineering application［J］．Automation of Electric Power Systems，2006，30(3):11-16．

［21］ 赵书强，李勇，王春丽．基于可信性理论的输电网规划方法［J］．电工技术学报，2011，26(6):166-171．

Zhao Shuqiang，Li Yong，Wang Chunli．Transmission network expansion planning based on credibility theory［J］．Transactions of China Electrotechnical Society，2011，26(6):166-171．

［22］ 艾欣，刘晓．基于可信性理论的含风电场电力系统动态经济调度［J］．中国电机工程学报，2011，31(增刊):12-18．

Ai Xin，Liu Xiao．Dynamic economic dispatch for wind farms integrated power system based on credibility theory［J］．Proceeding of the CSEE，2011，31(z1):12-18．

［23］ 艾欣，刘晓，孙翠英．含风电场电力系统机组组合的模糊机会约束决策模型［J］．电网技术，2011，35(12):202-207．

Ai Xin，Liu Xiao，Sun Cuiying．A fuzzy chance constrained decision model for unit commitment of power grid containing large-scale wind farm［J］．Power System Technology，2011，35(12):202-207．

［24］ 徐玖平，李军．多目标决策的理论与方法［M］．北京:清华大学出版社，2005．

［25］ Yang X S．A new metheuristic bat-inspired algorithm［J］．Nature Inspired Cooperative Strategies for Optimization，2012，284:65-74．