改进的粒子群优化算法下的MIMO雷达稳健波束形成
李敬军,孙维国,高伟伟,张曙,但波
(1.91208部队装备部,山东青岛266102;2.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)
改进的粒子群优化算法下的MIMO雷达稳健波束形成
李敬军1,2,孙维国1,高伟伟2,张曙2,但波1
(1.91208部队装备部,山东青岛266102;2.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)
在进行阵列自适应波束形成时,由于阵元导向矢量失配现象的存在,严重影响了常规最优波束形成的性能。考虑阵元的导向矢量误差,运用改进的粒子群优化算法对阵元的导向矢量进行纠正,使其误差达到最小,得到了一种适用于多输入多输出雷达的新的稳健波束形成方法。与现有的应用于MIMO雷达的稳健波束形成方法相比,在导向矢量误差较大或者误差随机变化的情况下新方法具有更高的输出信号干噪比,且其性能一直保持了较高的稳定性。数值仿真结果验证了新方法相比已有算法具有更好的鲁棒性和更高的输出性能。
MIMO雷达;稳健波束形成;导向矢量误差;粒子群优化算法;信号干噪比
MIMO雷达作为一种新体制雷达是近10年来雷达界的研究热点。MIMO雷达与常规雷达的区别在于发射端发射多个正交波束,在接收端形成虚拟天线阵列对多个发射波束进行接收,其虚拟天线阵列对应的虚拟接收导向矢量是发射导向矢量和接收导向矢量的Kronecker积的形式[1⁃2]。针对虚拟阵列的特性,文献[3⁃9]分别提出了不同准则下的波束形成方法,但都不是稳健的波束形成方法。如果导向矢量存在失配现象,与常规相控阵雷达相比,在进行波束形成的时候就不能单独考虑接收导向矢量的误差,而应考虑虚拟接收导向矢量的误差,也即是发射导向矢量和接收导向矢量两者的误差都要考虑,这样误差相比常规雷达要增大了许多,所以常规的稳健波束形成方法对于MIMO雷达来说将不再适合。对于稳健的MIMO雷达波束形成方法来说见诸报道的还较少,文献[10]提出了一种基于二阶锥规划(second⁃order cone program,SOCP)的稳健波束形成方法,但是该方法对于误差较大情况和随机误差情况下的性能下降严重,文献[11]则是在文献[10]基础上重点考虑了发射导向矢量的误差,与文献[10]存在类似的问题,二者本质上都是对角加载的方法,且运用内点法对锥规划求解时存在不可避免的初始值选取困难及易陷入局部最优等问题。
为了得到更加稳健的波束形成方法,运用改进的粒子群优化算法对导向矢量误差进行纠正,使存在误差的导向矢量无限接近真实的导向矢量,然后运用最小方差无失真响应方法进行最优波束形成。
1 MIMO雷达最优波束形成方法
考虑M发N收单基地的MIMO雷达系统。MI⁃MO雷达同时发射M组相互正交的波形,定义[1]:
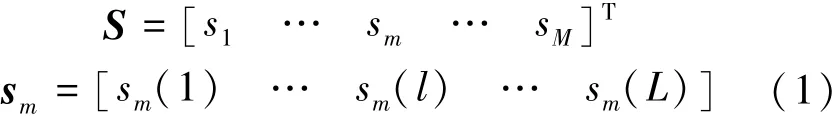
式中:m=1,2,…,M,l=1,2,…,L表示每组发射波形中一个发射周期内的子脉冲个数。定义目标位于远场,可以近似认定发射阵列与接收阵列位于同一位置,则雷达的发射导向矢量和接收导向矢量分别为[10⁃12]

式中:θ为波束指向,f为载波频率,τm(θ)(m=1,2,…,M)和τ'n(θ)(n=1,2,…,N)分别表示第m根发射天线到目标的时延和目标到第n根接收天线的时延。
远场条件下雷达回波可表示为[10⁃11]

式中:β表示目标反射系数,为了分析方便,可令β=1;Z表示除期望信号外的干扰与噪声分量,且与期望信号不相干。
对雷达回波进行匹配滤波后得到的滤波输出为

式中:Rss=SSH/L=IM,IM是M×M维单位矩阵,RZ=ZSH/L。将滤波输出按列拉直,得到MN×1维的矢量。
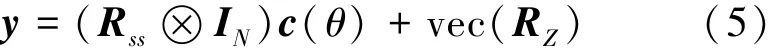
式中:IN是N×N维单位阵,c(θ)=a(θ)⊗b(θ),vec(·)表示矩阵的拉直操作。为了简化,这里将c(θ)、a(θ)和b(θ)简写为c、a和b。
定义波束形成权矢量为w=[w11…wN1w21…wNM]T,MVDR波束形成是通过限定波束形成器输出的期望信号功率恒定条件下其总的输出功率最小化,以达到输出SINR的最大化,其权矢量可通过式(6)来求解[13]:

运用拉格朗日乘子法求解式(6)得到MVDR最优波束形成权矢量:

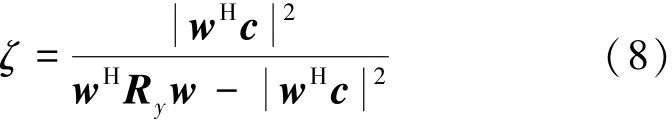
理论上MVDR波束形成是最小方差准则下的最优波束形成方法,在理想条件下可达到阵列的输出SINR达到最大。但是在实际应用的系统中,常常存在各种误差,如阵元幅相误差、信号协方差矩阵估计误差等,由于这些误差的存在,MVDR波束形成方法性能并不能达到最优。
2 IPSO算法在MIMO雷达稳健波束形成中的应用
2.1 导向矢量失配现象描述
导向矢量失配将导致期望信号相消的现象[14],即期望信号有可能会被当作干扰被抑制,这严重影响了系统的输出SINR性能。假定发射信号导向矢量和接收信号导向矢量都存在误差,两者都在一定的误差范围内。

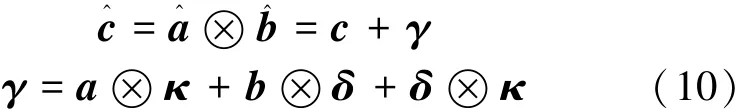
式中:c是真实的虚拟接收导向矢量,γ=[γ11…γN1γ21…γNM]T是虚拟导向矢量误差且γ中元素满足‖γnm‖≤ε,由于δ和κ是随机的,γ因此也是随机的。ε是一个凸集的上限,且ε=
由式(10)可知,MIMO雷达的导向矢量误差要比常规雷达的大许多,其对波束形成性能的影响将更大。文献[10]运用SOCP方法得到了稳健地波束形成方法,但是由于白噪声增益的限制,其对于导向矢量误差的限定为
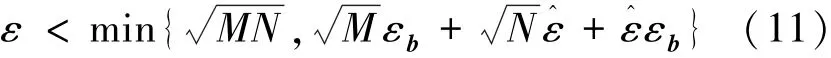
2.2 基于IPSO算法的稳健波束形成
2.2.1 算法的理论基础

要使式(12)达到最大,就是使其分子最大化而分母最小化,如果假定期望信号与干扰噪声不相关,则式(12)的最大化问题可以转换为下式的求解:
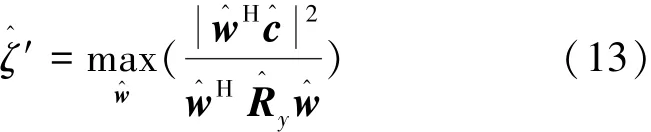
这里需要特别给出的是,由式(8)得到式(13)对应的理论值:

式(13)的求解等价于:
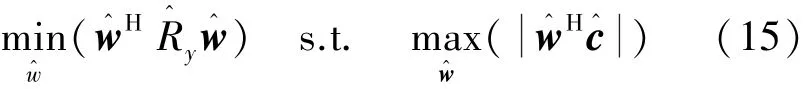
假定w^Hc>w^Hγ,式(15)中的约束条件运用柯西-施瓦茨不等式有
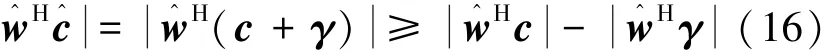
当且仅当γ=0时上式取等号,运用式(16),式(15)转换为

式(17)的求解存在尺度模糊且是非凸优化,为了消除尺度模糊可令w^Hc-w^Hγ=1,又因将w^进行相位旋转不改变式(17)的函数输出[10-11],所以式(17)可以转换为不存在尺度模糊的凸优化问题:

对于式(18)来说,实际情况下虚拟接收导向矢量c的误差γ是未知的,如果误差满足式(11)中的限定,通过式(18)得到的w^后将有较好的输出SINR,如果不满足限定条件,其输出信干噪比SINR将下降。如果可能采取某种策略将误差γ进行调整,使其趋于矢量0,也即是将式(18)转换为

式(19)实质是MVDR波束形成方法的的一种变换表达方式,如果将式(19)得到的w^代入式(13)则有
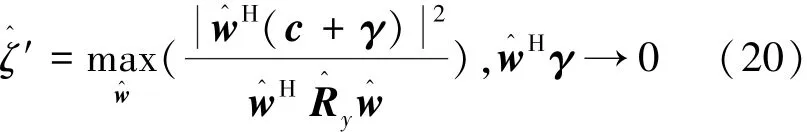
由式(19)知,式(20)是基于MVDR准则的,期望式(20)的值等于或无限趋近于式(14)。如前所述,误差γ可以认为是多个未知随机变量的集合,其元素满足‖γnm‖≤ε,如果要将式(19)进行求解,很显然是一个复杂的非线性约束优化问题。对于这种问题的求解有惩罚函数法、梯度投影法及PSO算法[15]等方法。PSO算法相对于惩罚函数法与梯度投影法等非智能算法而言具有一定优势,如对初值的选取要求不严,收敛速度更快,鲁棒性更高等优点。
2.2.2 IPSO算法分析
PSO算法本质上是一种基于迭代的智能优化算法,在波形优化、聚类分析、网络技术、粗糙集理论、超分辨分析等很多领域有着良好的应用效果。
假设粒子群规模为P,每个粒子的维数为NM,PSO算法的迭代次数为K,则第k(k=1,2,…,K)代粒子第i(i=1,2,…,P)个粒子第d(d=1,2,…,NM)维元素的更新公式为[21]
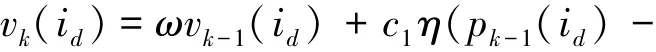
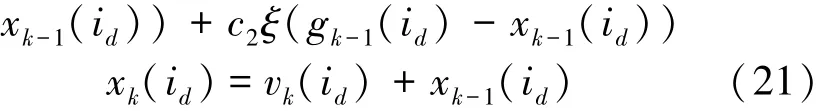
式中:vk(id)和vk-1(id)分别是第k代和第k-1代的更新速度,pk-1(id)和gk-1(id)分别是第k代更新之前的个体最优值和全局最优值,xk(id)和xk-1(id)分别是第k代和第k-1代的个体值,ω是惯性权重系数,c1和c2是学习因子,η和ξ是[0,1]间的随机数。
当导向矢量存在失配时,在MIMO雷达稳健波束形成的时候,权矢量w^的求解是一种函数优化问题,所以可以直接应用式(21)来求取。而根据2.2.1节的分析,运用PSO算法求解波束形成权矢量的代价函数定义为

为了提高PSO算法的收敛速度并且降低其陷入局部最优的可能性,现将算法的运行过程改进:
1)为了使算法能够达到更快的收敛速度,首先对于初始粒子群中个体的位置,不采用随机生成的模式,而是根据导向矢量误差界限ε,将P个粒子均匀放置,使其导向矢量误差位于[-ε,ε]范围内;其次,在更新过程时,对粒子到达的位置进行记录,并对其中差的位置进行锁定,在下一次更新时,粒子将跳过这些位置,简称这些位置为“禁忌点”。
2)在考虑算法收敛速度的同时,还应考虑粒子在更新过程中陷入局部最优的可能性,具体方法为:当粒子更新过程中,运用代价函数(22)对粒子进行评价,如果k(k≫1)次更新后产生的全局最优值始终在一个较差的范围(e大于期望值),则将粒子全局最优值在第d维进行变异操作,第d维的选取采用式(23)解得
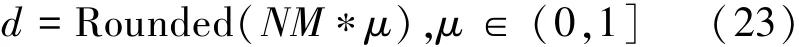
式中:Rounded(·)表示取整操作,NM是粒子的维数,μ是随机数。变异的方式为随机产生一个导向矢量误差在[-ε,ε]范围内的值且需跳过之前记录的禁忌点,然后对全局最优值的第d维进行替换,最后运用新得到的全局最优值和式(21)对所有的粒子进行更新。这种变异操作与遗传算法中的变异操作类似,都是针对某位进行随机变异,但是变异的范围因为禁忌点的存在相比遗传算法要小。
由上述分析,IPSO算法相比传统的PSO算法的改进主要在于初始化设置、禁忌点标记以及变异操作上,其流程图如图1所示。
IPSO算法的运行步骤为:
1)初始化:产生P个粒子,每个粒子的导向矢量误差均匀分布于[-ε,ε]范围内,并设定初始的更新速度v0(id),运用代价函数式(22)对所有粒子进行评价,粒子当前值设为个体最优,个体中最优的设为全局最优;
2)更新:利用式(21)对所有粒子进行更新操作,并运用式(22)进行评价判断是否需要替换个体最优值和全局最优值;
3)屏蔽:对较差的粒子位置进行标记,并在下次更新时跳过这些位置;
4)变异:判断k次(k的取值视情况而定,可以是一次k次迭代,也可以是多次k次迭代)迭代后的全局最优值与理论值的误差e的大小,如果超过要求,则运用式(23)进行变异操作,如果未超过而又未达到设定要求则转到2);
5)终止:判断误差e是否达到设定要求,如果达到,则记录全局最优值并退出算法,反之,则转向2)。
从以上分析可以看出,基于IPSO算法的稳健自适应波束形成算法转换成为了一种约束优化问题,即是在限定条件下对于波束指向的寻优过程。

图1 IPSO算法Fig.1 IPSO algorithm
3 仿真分析
假定MIMO雷达系统的配置为M=8发N=8收的单基地雷达,载波波长为λ,相邻发射阵元和相邻接收阵元间距均为dt=dr=λ/2,远场条件下8组编码长度为128的相互正交的四相编码信号被8根天线分别同时发射,期望信号真实方向为θ=0°,信噪比范围为SNR∈[-35,10]dB。第1个干扰信号的方向为θ1=30°,干噪比(INR)为25 dB,第2个干扰信号的方向为θ2=50°,干噪比为35 dB.运用IPSO算法进行仿真验证,与已有的MVDR方法和SOCP方法进行比较,并给出了理论值作对照。
仿真1 假定ε^=εb=2.5,若ε满足式(10),即要求ε<8,这里取ε=7,规定γ中的元素相同,分别运用MVDR、SOCP和IPSO算法进行仿真,仿真结果如图2(a)。从图2(a)可以看出,SOCP方法在SNR<-12 dB时具有较好的性能,但是随着期望信号输入信噪比的增大,其性能下降较为严重,常规的MVDR自适应波束形成算法在SNR<-15 dB时性能较为平稳,但是其性能与IPSO算法和SOCP方法差7 dB左右,在SNR>-15 dB时其输出SINR性能则急剧下降,可以说其输出SINR性能一直表现较差,而新的稳健波束形成算法则一直保持了较好的输出SINR性能,在其性能稳定段(输入SNR大约在-35~5 dB)其与理论值的差距一直维持在2.7 dB左右,满足输出SINR损失小于3 dB的要求;如果δ和κ中的元素在εa、εb限定范围内,随机产生满足高斯分布且ε=7的γ中元素,运用3种算法进行仿真,其结果如图2(b)所示。
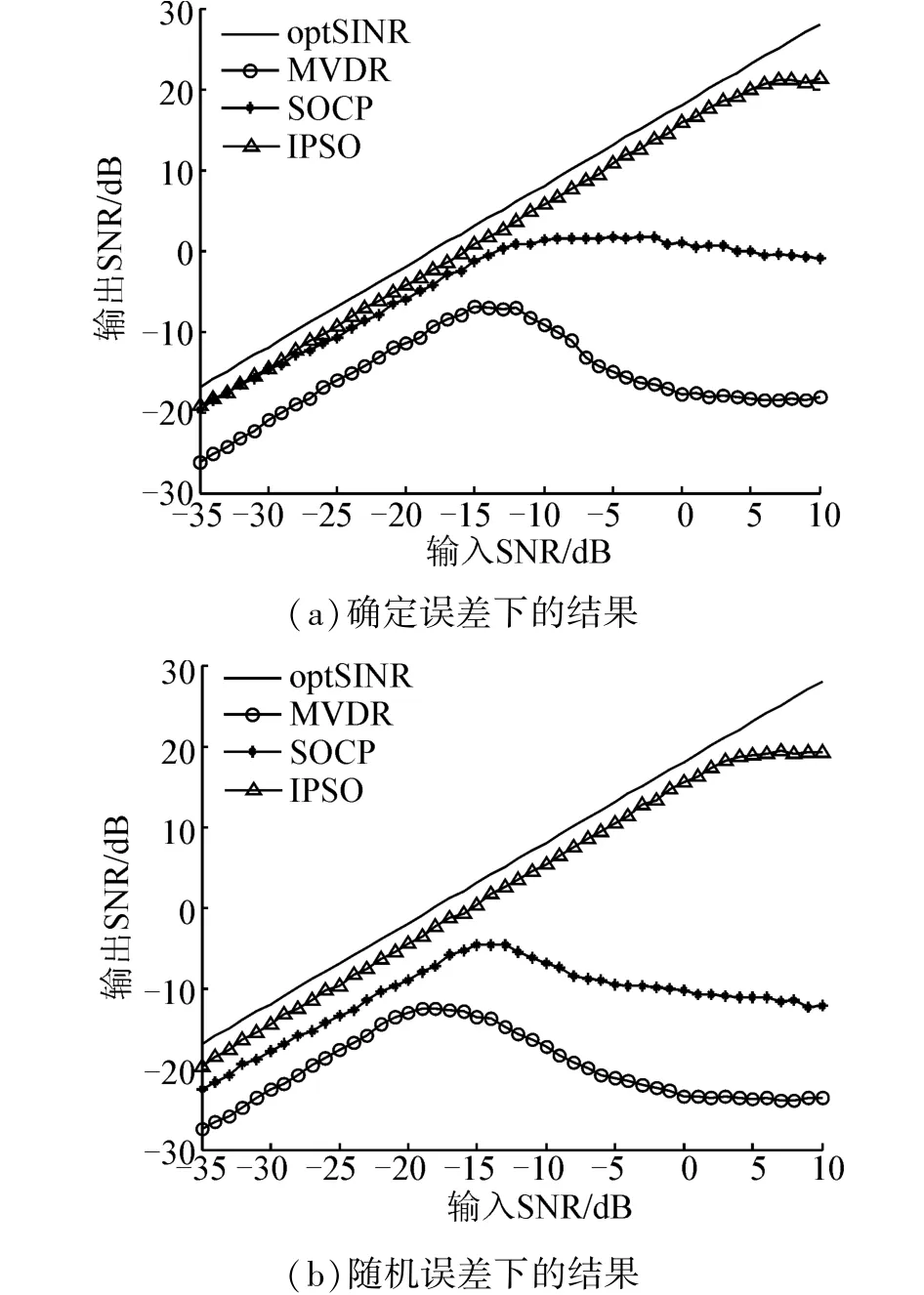
图2 输出SINR与输入SNR关系(ε=7)Fig.2 Output SINR versus input SNR(ε=7)
可以看出在随机误差情况下,SOCP方法和MVDR方法性能下降更为严重,而IPSO算法则仍然保持了较好的性能,在算法性能的稳定阶段其与理论输出SINR值得差距仍大约为2.7 dB,符合实际工程的要求。之所以有如此仿真结果,与IPSO算法是针对误差矩阵中的每一个元素进行操作且IPSO算法的全局性更优有关,而SOCP方法是针对误差矩阵的整体操作且在运用内点算法时更易陷入局部最优解,MVDR方法则并不是稳健的波束形成方法。
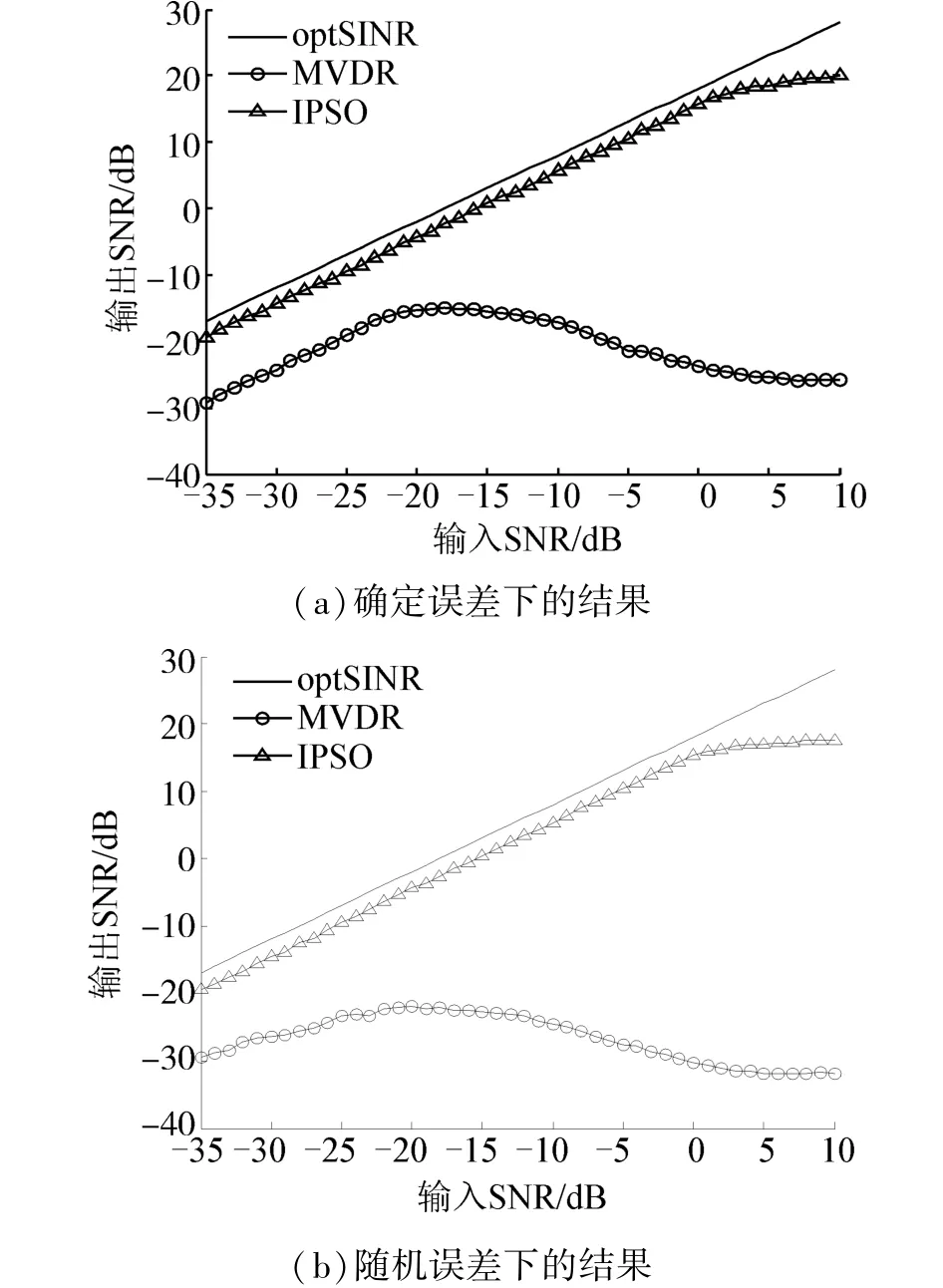
图3 输出SINR与输入SNR关系(ε=20.392)Fig.3 Output SINR versus input SNR(ε=20.392)
如果取ε=20.392,限于SOCP方法的适用范围(式(10)),其性能已得不到保证,IPSO算法下的波束形成是在MVDR方法基础上的改进,所以仅将IPSO算法与MVDR方法进行比较。除ε取值外,仿真结果图3(a)中条件对应图2(a)中条件,图3(b)中条件对应图2(b)中条件。结果显示,无论在确定误差的情况还是随机误差的情况,常规的MVDR自适应波束形成算法的性能一直非常差,且随机误差情况下更差,不适宜应用于导向矢量存在误差情况下的MIMO雷达波束形成。而改进的连续PSO算法下的自适应波束形成算法则一直保持了良好的性能,但是其输出SINR的性能稳定段较ε=7时变短,其稳定段大约变为-35 dB到2 dB,在性能稳定期间其输出SINR值与理论输出SINR值的差距大约为2.9 dB左右,符合输出SINR值损失小于3 dB的要求。
图2和图3通过导向矢量存在确定误差或者随机误差情况下的输出SINR充分说明了IPSO算法相比SOCP方法和MVDR方法具有更高的稳健性与适应性,且对于误差随机变化的情况及较大误差的情况具有更好的误差容忍性,从仿真结果还可以看出新的算法对于期望信号输入SNR较低的情况更加适用。
4 结束语
提出的基于IPSO算法的稳健最优波束形成方法适用于MIMO雷达。新方法本质仍是MVDR方法,但是巧妙的利用IPSO算法将波束形成转换为波束指向寻优的过程,对阵元导向矢量误差进行纠正,使纠正后的导向矢量无限接近于真实的导向矢量,从而其输出SINR与常规的MVDR和基于二阶锥规划的波束形成方法相比具有更好的性能。仿真结果验证了新方法的良好性能。
[1]LI J.MIMO radar signal processing[M].[S.l.]:John Wi⁃ley and Sons,2009:20⁃29.
[2]FRIEDLANDER B.On the relationship between MIMO and SIMO radars[J].IEEE Transactions on Signal Processing,2009,57(1):394⁃398.
[3]WANG W Q.Phased⁃MIMO radar with frequency diversity for range⁃dependent beamforming[J].IEEE Sensors Jour⁃nal,2013,13(4):1320⁃1328.
[4]HE J,FENG D Z,YOUNAN N H,et al.Bi⁃Capon beam⁃forming for MIMO radar:a correlation matrix⁃based method[C]//Proc of the IEEE CIE International Conference on Radar.Chengdu,China,2011:335⁃338.
[5]DULY A J,LOVE D J,KROGMEIER J V.Time⁃division beamforming for MIMO radar waveform design[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1210⁃1223.
[6]WANG W J,NARAYANAN R M.CGLRT plus TDL beam⁃forming for ultrawideband MIMO noise radar[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(3):1858⁃1869.
[7]ABRAMOVICH Y I,FRAZER G J,JOHNSON B A.Itera⁃tive adaptive Kronecker MIMO radar beamformer:descrip⁃tion and convergence analysis[J].IEEE Transactions on Signal Processing,2010,58(7):3681⁃3691.
[8]HONG Z Q,MA P,HUANG Z R,et al.Adaptive beam⁃forming for MIMO radar with sidelobe control based on sec⁃ond order cone programming[C]//Proc of the IEEE Inter⁃national Conference on Information Science and Technology.Wuhan,China,2012:384⁃388.
[9]洪振清,张剑云.一种降维的MIMO雷达MVDR波束形成算法[J].信号处理,2011,27(8):1184⁃1188.HONG Zhenqing,ZHANG Jianyun.A dimension⁃reduced MVDR beamforming algorithm for MIMO radar[J].Signal Processing,2011,27(8):1184⁃1188.
[10]XIANG C,FENG D Z,LYU H,et al.Robust adaptive beamforming for MIMO radar[J].Signal Processing,2010,90(12):3185⁃3196.
[11]王勇,刘宏伟,纠博,等.MIMO雷达稳健的发射波束形成算法[J].电子与信息学报,2012,34(2):318⁃323.WANG Yong,LIU Hongwei,JIU Bo,et al.Robust trans⁃mitting beamforming for MIMO radar[J].Journal of Elec⁃tronics and Information Technology,2012,34(2):318⁃323.
[12]WANG H Y,LIAO G S,WANG Y,et al.On parameter identifiability of MIMO radar with waveform diversity[J].Signal Processing,2011,91(8):2057⁃2063.
[13]VOROBYOV S A,GERSHMAN B,LUO Z Q.Robust adap⁃tive beamforming using worst⁃case performance optimization:a solution to the signal mismatch problem[J].IEEE Trans⁃actions on Signal Processing,2003,51(2):313⁃324.
[14]SOMASUNDARAM S D.Linearly constrained robust capon beamforming[J].IEEE Transactions on Signal Processing,2012,60(11):5845⁃5856.
[15]KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proc of the IEEE International Conference on Neural Networks.[S.l.],1995:1942⁃1948.
[16]SHI Y,EBERHART R.A modified particle swarm optimi⁃zer[C]//Proc of the IEEE World Congress on Computa⁃tional Intelligenee.Anchorage,USA,1998:69⁃73.
Robust beamforming in MIMO radar by using the IPSO
LI Jingjun1,2,SUN Weiguo1,GAO Weiwei2,ZHANG Shu2,DAN Bo1
(1.Department of Equipment,91208 Army,Qingdao 266102,China 2.College of Information and Communication Engineering,Har⁃bin Engineering University,Harbin 150001,China)
Conventional optimal beamforming has poor performance when the array steering vector is inaccurately known.In adaptive beamforming,the mismatch phenomenon of array steering vector seriously affects the conven⁃tional optimal beamforming performance.Taking into account the steering vector mismatch of array elements,the improved particle swarm optimization(IPSO)algorithm is used to correct the array steering vector,to minimize the mismatch and to obtain a new robust beamforming method that adapts to multi⁃input and multi⁃output(MIMO)ra⁃dar.Compared with the existing algorithms,this method has a better output signal to interference plus noise ratio(SINR)when the steering vector mismatches are large or the error changes randomly and its performance always keeps a high stability.Numerical experiments validated that the proposed method has better robustness and higher performance than existing algorithms.
MIMO radar;robust beamforming;the steering vector mismatches;IPSO algorithm;signal to interfer⁃ence plus noise ratio
10.3969/j.issn.1006⁃7043.201310079
TN958
:A
:1006⁃7043(2015)06⁃0851⁃06
http://www.cnki.net/kcms/detail/23.1390.u.20150428.0911.013.html
2013⁃10⁃27.网络出版时间:2014⁃04⁃28.
国防基础研究基金资助项目(40106030503)
李敬军(1982⁃),男,助理研究员,博士;孙维国(1972⁃),男,部长,学士.
李敬军,E⁃mail:li_jingjun@163.com.

