分离式承台摇摆抗震及其有限元模拟

杨浩林，袁万城

（同济大学土木工程防灾国家重点实验室，上海200092）

分离式承台摇摆抗震及其有限元模拟

杨浩林，袁万城

（同济大学土木工程防灾国家重点实验室，上海200092）

为了提供一种桥梁抗震的可选方案，根据摇摆抗震的基本思想，阐述了自复位分离式承台的构想，将传统桥梁桩基础的承台一分为二，使承台上部能够在地震作用下摇摆，从而在基础部位隔断地震传播途径，达到减隔震的目的。分析了该抗震方法的抗震原理，阐释了该抗震方法可能采用的各种构造工艺与施工方式。传统的摇摆抗震数值模拟技术将摇摆接触面区域视为刚体，不考虑接触面的弹性变形，与实际情况不符，故采用了将摇摆区域（文中为承台）采用三维实体有限元模拟的精细化建模方法，并与传统的建模方法进行对比。分析表明：在现有的桥梁抗震设计技术与施工技术支持下，分离式承台具有工程应用的可能性，在有限元模拟中，将摇摆区域视为刚体的做法会放大结构的位移响应，是一种偏保守的做法。

分离式承台；摇摆抗震；自复位；抗震设计；桥梁

通过对历史上多次地震中桥梁震害分析，桥梁工作者们发现，将桥梁设计为在地震中完全弹性抗震既不经济也难以实现抗震目标，一些弹性强度不足的桥梁能够在地震中形成塑性铰，延长自身周期，减小结构受到的地震动内力，并且通过滞回耗能，进一步减小结构位移响应，从而在地震中幸存。基于此，目前桥梁抗震的一个基本思路是，通过合理的强度设计或者局部构造设计，适当降低桥梁在地震作用下的刚度，延长结构周期，体现在桥梁抗震设计规范中即为设置能力保护区域的延性抗震设计与采用减隔震支座的减隔震设计，与此同时，为了防止落梁或桥墩倒塌等恶性震害的发生，越来越多的工程师希望桥梁在地震下能够具有自复位功能。对长细比较小的“矮胖”桥墩而言，桥墩地震响应主要表现为受剪，此时支座减隔震可获得较好的效果，一些支座经过特殊设计，可以完成自复位功能，如双曲面支座等，但此类支座通常构造复杂，价格昂贵；对于长细比较大的“高瘦”桥墩而言，桥墩地震响应主要表现为受弯，墩顶支座减隔震性能不易发挥，墩底较易形成塑性铰，故此类桥梁较适宜利用延性抗震，但利用延性抗震塑性铰区域会发生不可逆的塑性变形，且不具备自复位功能，震后修复工作较为繁重，故有必要开发一种新的方法，为桥梁提供其他可行的自复位抗震方案。

本文在已有抗震设计原理的基础上，介绍了分离式承台摇摆抗震技术的抗震原理，并在分析已有摇摆抗震模拟方法的优缺点之后，介绍了采用实体有限元单元模拟摇摆区域的精细化模拟方法，并以一座4跨连续梁为例，考察了该模拟方法的有效性。

1 分离式承台抗震原理

1.1 分离式承台的原理

延性抗震设计理念使桥梁在地震作用下在预先设计的部位形成塑性铰（图1 B）。进一步减弱塑性铰区域刚度，则发展出了桥墩摇摆抗震（图1 C），桥墩摇摆优势在于其隔震构造简单，地震能量传递路径在摇摆处即被切断，并且具有自复位能力。如图2，已建成的新西兰南Rangitikei高架桥［1］采用了桥墩摇摆抗震，桥墩在地震动作用下向上提离并摇摆，并通过框架墩底凸榫结构与剪力销来限制墩底摇摆部位的横向滑动。但南Rangitikei高架桥的优势在于其为框架墩桥梁，其摇摆机制类似建筑结构框架摇摆［2］，对于单墩桥梁而言，其墩底面积较小，容易出现桥墩边角外层混凝土压溃，产生弯矩退化现象，鲁棒性不如扩大基础［3］，若要保证单墩摇摆的有效性，可添加额外的耗能装置，如图3，但其构造复杂，且刚度配置较为棘手［4］。扩大基础摇摆的优势在于其力臂长，同样自重下可以提高回复力矩，桥梁摇摆过程中不易产生倾覆，但对地基要求较高［3］，且扩大基础泛用性不如常见的桩基础。

图1 分离式承台发展示意图Fig.1 Diagram of separated pile⁃cap

图2 南Rangitikei高架桥构造图Fig.2 Schematic of south Rangitikei viaduct

图3 单墩摇摆系统构造图Fig.3 Schematic of single pier rocking system

参考扩大基础摇摆机理，并结合在我国广泛采用的群桩基础的构造特点，将承台一分为二，使单墩桥梁摇摆区域从墩底移动至承台中部，使承台上半部分能够随桥墩及上部结构一起提离，使承台上部形成类似扩大基础的结构，完成摇摆行为（图1 D）。此方法可称为分离式承台摇摆抗震方法［5］。

1.2 分离式承台的构造

分离式承台的基本设计目标是：1）承台在静力荷载作用下与普通承台无异，在地震作用下，承台能够产生竖向提离进行摇摆，并由自重产生回复力完成自复位；2）限制任何荷载作用下的承台横向滑移；3）添加竖向提离限位装置，阻止结构可能产生的过大位移；4）合理设计承台层间接触刚度，使上部承台在回落时能够耗能减震，下部承台与桩基础保持弹性。为实现目标1、2，可在层间设置凸榫或用承台下部包围其上部（如图4 D⁃1～D⁃3），并合理布置内部钢筋网，保持转角、边角与应力集中处的弹性。为实现目标3，可以在承台内部设置无粘结预应力筋或无粘结限位钢筋（如图4D⁃4），通过预埋保护套可实现钢筋的后张或其他布置；或在承台外部设置钢套箍或拉索限位装置（如图4中D⁃5～D⁃6），通过预埋限位部分内部构件，后期焊接外部构件或限位构造整体预制预埋，也可实现此限位构造。为了实现设计目标4，可以在任何构造的分离式承台层间设垫层（如图4中D⁃7），此垫层的厚度、刚度与强度等特性均可根据设计目标自主选择，随着材料科技的发展，各种高新缓震耗能材料或各种复合材料均可布置于此，不同材料的组合布置（如上层材料塑性变形耗能，中层材料受压升温挥发耗能，下层材料弹性缓震）也可实现。在合理设计下，分离式承台可以完成预期的抗震目标。

图4 分离式承台构造原理图Fig.4 Schematic of separated pile⁃cap

1.3 现阶段摇摆抗震的模拟方法

摇摆抗震最早可追溯到Housner［6］关于高位水槽摇摆的研究，Espinoza［7］进行了扩大基础振动台实验及对应的2维集中质量多弹簧有限元模型模拟，Kawashima［8］进行了扩大基础振动台实验及对应的3维分布质量考虑塑性铰的弹簧矩阵模型模拟，NCREE研究中心进行了扩大基础实验及对应的2维集中质量考虑墩底塑性铰的多弹簧模型模拟［9⁃10］，夏修身［11］提出了模拟桥墩摇摆2维分布质量多弹簧模型、双弹簧模型与单转动弹簧模型。

上述学者在模拟摇摆时，其共同特点是：1）墩身大部分采用杆单元模拟；2）摇摆接触面局部考虑为刚体；3）除转动弹簧模型外，摇摆接触面采用抗压弹簧单元模拟。但将摇摆基础考虑为刚体，与实际情况不符，不能观察基础在地震中的变形与局部提离，故本文采用实体有限元单元进行摇摆接触面局部模拟的精细化模拟方法，并将精细化模拟方法与传统的模拟方法进行对比，以期观察不同模拟方法下，摇摆响应的异同。洪晓慧等［10］的研究表明合理设计后的摇摆体系可以保证桥墩底部不发生屈服［10］，故本文之后的数值分析内容均不涉及桥墩出现塑形的情况；夏修身的研究［11］验证了当不考虑墩底产生塑性铰，且摇摆接触面上部构造采用刚体模拟时，双弹簧模型的计算效率更高且精度较高，故本文在该类模型中，均采用两弹簧模型。

2 算例以及模拟方法

本文算例为一联采用桩基础的四跨连续梁（图5），桥梁细部尺寸见图6，部分截面细节列于表1，下部结构采用C40混凝土，主梁采用C50混凝土。

图5 算例桥梁侧视图Fig.5 Side view of the target bridge

图6 桥梁下部结构细部尺寸图Fig.6 Detailed dimensions of the substructure

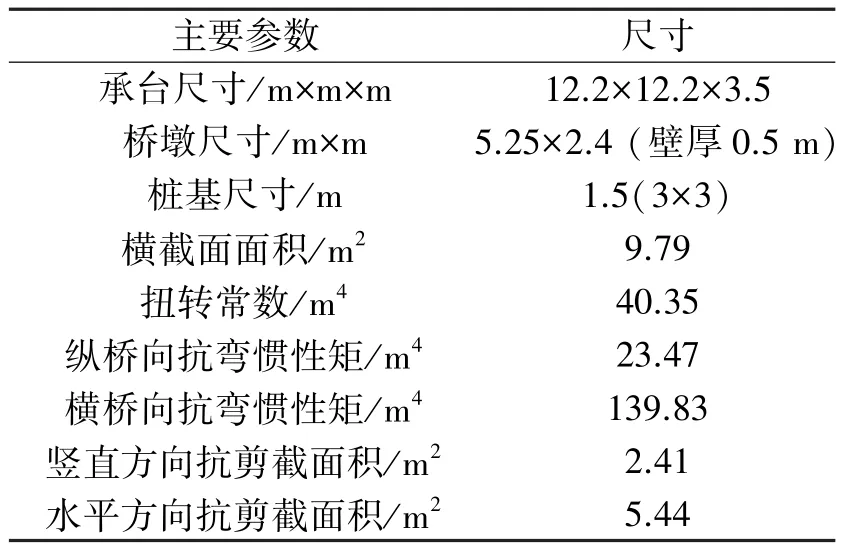
表1 有限元模型主要参数与尺寸Table 1 Main dimensions of finite element model

建模方法分为精细化模型与简化模型两大类，具体建模方法如下所述：

精细化模型（下文称模型1）如图7所示，将中间固定墩承台按上半部分2 m，下半部分1.5 m的方式改造为分离式承台，并采用实体单元模拟，将上下2层承台分别划分为4×4各16个，共32个实体单元，每层实体单元相邻单元共用节点，上下两层实体单元不共用节点，本文采用的sap2000有限元软件中弹簧单元长度不能为0，分离层部分预留0.1 mm空隙（如采用可建立0长连接单元的有限元软件，此长度可取为0），用于建立5×5多段线性弹簧矩阵，弹簧两端与分离层上下实体单元共用节点，将上下2层承台连接起来。弹簧本构关系如图8所示，K1为抗压刚度，在传统扩大基础摇摆模型中，此刚度取为Winkler土弹簧刚度，而本模型中接触面下部为混凝土，弹簧单元仅起到传力作用，不考虑碰撞耗能，将此处考虑为刚性接触，弹簧刚度取为1×108kN／m，若加入了分离层缓冲材料，此弹簧刚度可另行调整；若加入了耗能材料，此弹簧单元可换为其他带阻尼特性的接触单元。D为弹簧自由变形长度，本文不考虑提离限位装置，故D取为无穷大，若加入了限位装置，此处D可取为设计自由提离高度，当承台提离超过D时，可加入第3段刚度模拟限位装置的限位行为。群桩采用杆单元模拟，在距承台底部5 m处固结。桥墩及主梁采用杆单元模拟，固定墩墩梁连接处固结，活动墩处直接赋予理想边界条件，在计算时考虑结构自重作用。

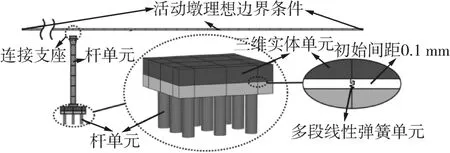
图7 精细化建模示意图Fig.7 Diagram of elaborate finite element model

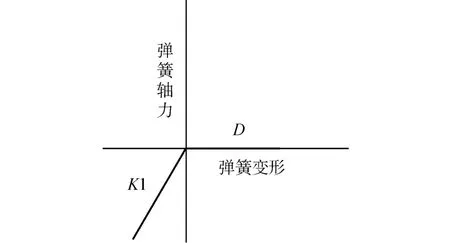
图8 多段线性弹簧单元本构示意图Fig.8 Constitutiverelation of multi⁃elastic link element

传统简化模型共分为3种，多自由度带桩基模型（下文称模型2）、多自由度无桩基模型（下文称模型3）与单自由度无桩基模型（下文称模型4）。

模型2如图9所示，将主梁质量全部集中在墩顶，添加墩顶反力，墩身采用杆单元模拟，考虑墩身质量及自重，墩底和上部承台底部中心用刚臂连接，在上下部承台中心建立质点，考虑全部承台质量与自重，上部承台底部与下部承台顶部各自向外伸出6.1 m的2个刚臂，刚臂的末端用如图8所示的多段线性弹簧连接，连接单元长度0.1 mm，群桩基础采用杆单元建立，桩长5 m，桩顶与承台用刚臂连接，桩底固结，考虑桩身质量与自重。

图9 多自由度有桩基简化模型建模示意图Fig.9 Diagram of multi⁃DOF finite element model with pile group

模型3如图10所示，不考虑分离层以下部分在地震过程中对结构其余部分的影响，分离层以上建模方法与模型2相同，上部承台底部向外伸出的2个刚臂末端赋予如图8所示的多段线性弹簧连接，弹簧单元长度0.1 mm，弹簧另一端固结。

图10 多自由度无桩基简化模型建模示意图Fig.10 Diagram of multi⁃DOF finite element model without pile group

模型4模拟方法如图11所示，墩身采用杆单元模拟，考虑刚度但不考虑质量，仅为墩身赋予自重荷载，其余部分与模型3相同。

图11 单自由度无桩基简化模型建模示意图Fig.11 Diagram of single⁃DOF finite element model without pile group

3 不同模拟方式对分离式承台的影响

3.1 模型基本特性与差异的分析

从表2可以看到，结构在第1周期上的差别并不大，模型1考虑了墩身、全部承台以及桩基，模型2承台作为刚体处理，模型3与模型4分离层以下全部省略，对第1周期而言，模型1的质量最大，刚度最低，周期最大；模型2考虑了桩基与承台质量，质量与模型1相同，但由于接触面为刚体，承台简化为质点，刚度较模型1大，周期次之；模型3不考虑分离层以下部分，周期更小；模型4不考虑墩身质量，周期最小。表中的周期为结构线性状态下的周期，不反映结构进入摇摆状态以后的动力特性变化。

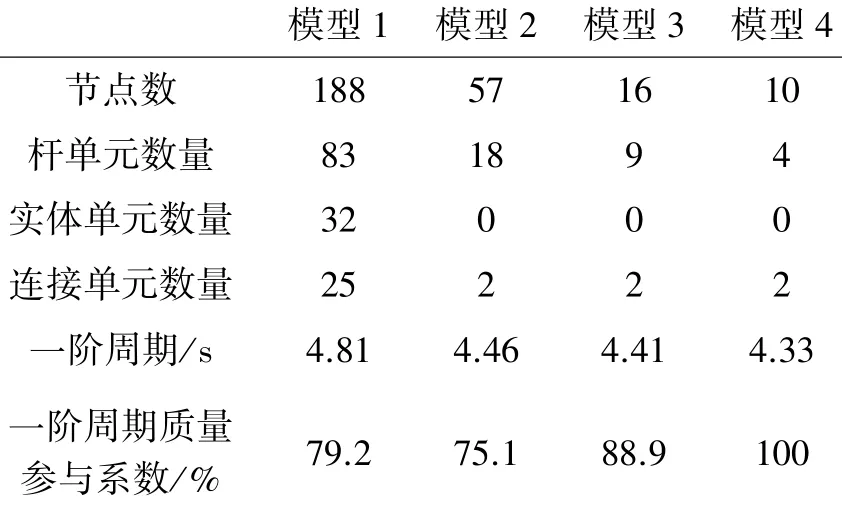
表2 4种有限元模型特性比较Table 2 Comparison of 4 finite element models

为了比较不同模型在相同地震作用下响应的差异，荷载输入采用了同一反应谱生成频谱较为丰富的3条时长为30 s的人工地震波，特征周期0.75 s，地震动峰值加速度为0.4 g，地震动加速度时程如图12所示。地震反应计算采用非线性直接积分进行时程分析，积分方法采用HHT法，地震波输入方向为纵向自左向右，承台左侧称A端，右侧称B端（见图5）。为了分析有限元模型的地震响应行为特点，记录各个模型在3条地震波作用下的摇摆提离响应，墩底弯矩响应、墩顶位移响应。为了验证和比较模型的自复位效果，计算时长取为80 s。

图12 人工地震波加速度时程Fig.12 Acceleration time⁃history of the artificial seis⁃mic wave

由表3可以看到，精细化模型虽然自由度较多，计算量较大，但仍然在可接受范围以内。对比最大墩底弯矩，模型1与模型2、3相差较小，而模型4则明显偏小，这主要是由于单自由度模型不存在墩底弯矩震荡，本文3.3节中会着重分析。在位移变形方面，模型2、3、4的最大墩顶位移与承台提离均大于模型1，说明用简化模型来估算分离式承台的最大位移是偏保守的，承台变形对于承台提离程度大小有明显的影响。另外模型1的位移响应明显小于模型2，而模型2与模型3之间则相差很小，说明在分离式承台中承台自身的变形对结构的位移响应影响也较大。

表3 4种有限元模型时程分析比较Table 3 Comparison of 4 finite element models in time⁃history analysis

3.2 承台提离响应比较

如图13是3号地震动作用下承台两侧提离时程，对比4种模型的承台提离响应，两侧提离的开始时刻、峰值时刻与结束时刻吻合得较好，说明精细化模型的模拟是有效的。对比提离峰值，简化模型明显大于精细化模型，这是因为精细化模型中在承台发生提离时，上下承台均会发生变形，故减小了上下承台的相对提离。以上对比说明用传统简化模型可以正确地反应结构在地震中的提离时刻与提离次数，但会放大承台的提离峰值。

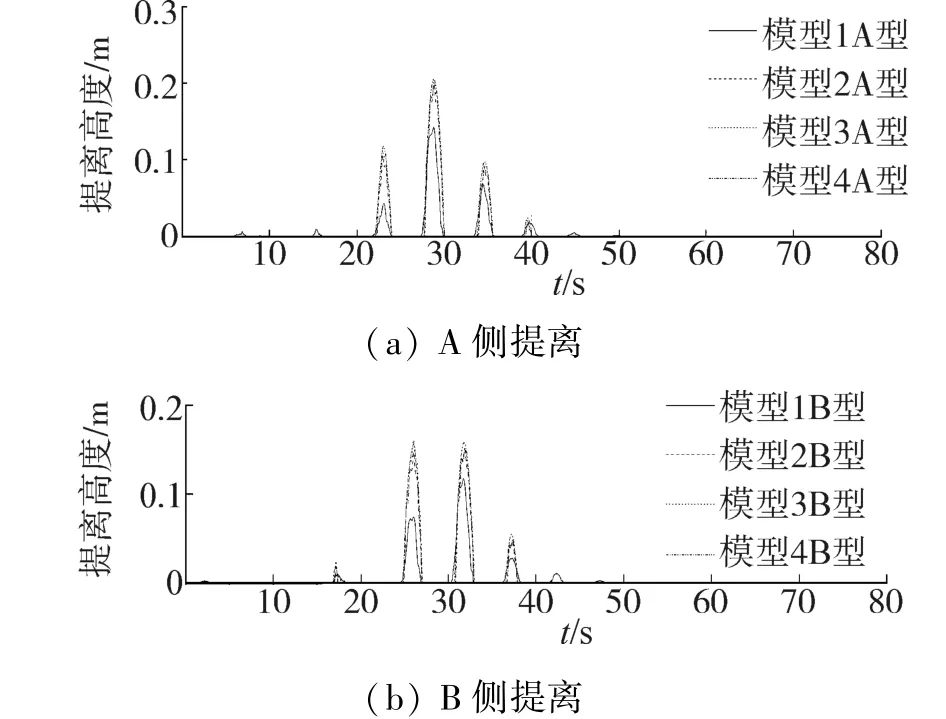
图13 承台两侧提离响应Fig.13 Lifting response of the cap

3.3 墩底弯矩响应比较

如图14是1号地震动作用下墩底弯矩时程，对比数据可以发现，4种不同建模方法的墩底弯矩反应有局部的差异，在结构进入摇摆之前，精细化建模的墩底弯矩在大部分情况下小于简化模型；在自复位阶段，模型1的弯矩衰减也要快于简化模型，其主要原因是模型1考虑了下部承台与群桩基础的相互作用，在地震作用下，下部承台与群桩基础会与结构其他部分一起运动，墩底相对承台变形较小，而模型2虽然考虑了下部承台与群桩基础，但由于承台被视为刚体，无法像实体单元般发生变形，故模型2的响应特点与模型3更为接近。另一方面，模型4墩底弯矩在进入平台段之后，不会出现锯齿状的震荡，原因主要是，在其他3个多自由度模型中，在承台提离以后，墩身依然会按照高阶振型振动，而单自由度结构不存在高阶振型，所以墩底弯矩平台是一段直线。

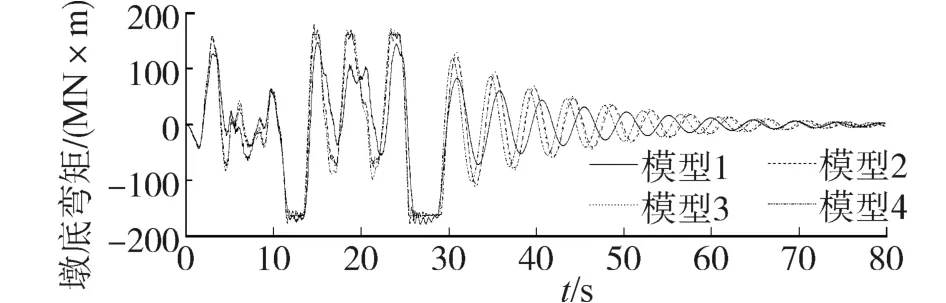
图14 墩底弯矩响应比较Fig.14 Moment response at the bottom of pier

3.4 墩顶位移响应比较

如图15是3号地震动作用下墩顶位移时程，对比4种模型的墩顶位移，在地震能量积累阶段与摇摆阶段，精细化模型与传统简化模型的响应拟合情况较好，说明两类模型在估算墩顶位移方面可以相互验证。另外可以看到，4种模型的墩顶位移最大值均出现在同一时刻，且简化模型的最大值大于精细化模型，考虑到实际情况中还存在碰撞耗能以及其他阻尼作用来减小地震响应，用简化模型来估算分离式承台的最大墩顶位移是偏保守的。在自复位阶段，精细化模型的摇摆周期大于简化模型的周期，且各模型摇摆周期均与各自的第1周期非常接近，故可以认为结构在自复位阶段的位移衰减周期是按照第1周期进行的。

图15 墩顶位移响应比较Fig.15 Displacement response on the top of pier

精细化模拟最大的优势在于通过实体单元模拟摇摆接触面，可以反映接触面局部在摇摆过程中的变形。由于考虑到计算效率等因素，本文在进行精细化建模时，承台实体单元数量并不多，但可以预见在不久的将来，随着计算机技术的高速发展，在可接受的计算时间下，可以采用精细化建模方法将承台网格进一步细化，获得更加详细摇摆接触面的信息。

4 结论

本文详细分析了分离式承台的抗震原理以及可能的施工方法和构造工艺。详细介绍了分离式承台摇摆抗震的精细化模拟方法，分析了其与传统模拟方法在建模思路，及在地震作用下，承台提离、墩底弯矩以及墩顶位移的异同点，主要结论有：

1）在现有的桥梁抗震设计技术与施工技术支持下，分离式承台具有工程应用的可能性。

2）精细化模型的各项地震响应都能与传统模型基本保持一致，说明采用实体单元与杆单元结合的方法来模拟摇摆抗震技术是可行的；传统模型将承台视为刚体时，忽略承台变形，放大了承台提离的程度。

3）在本多跨连续梁算例中，主梁质量较大，只考虑主梁质量的单自由度简化模型可以反映分离式承台的动力特性与地震响应特点，也反应出了分离式承台与其他摇摆抗震方法的共性；但由于其不存在高阶振型，不能正确反映摇摆过程中墩底弯矩时程的锯齿形震荡。

［1］PALERMO A，PAMPANIN S，CALVI G M.Concept and development of hybrid solutions for seismic resistant bridge systems［J］.Journal of Earthquake Engineering，2005，9（6）：899⁃921.

［2］CHENG C T.Shaking table tests of a self⁃centering designed bridge substructure［J］.Engineering Structures，2008，30（12）：3426⁃3433.

［3］DENG L，KUTTERB L.Characterization of rocking shallow foundations using centrifuge model tests［J］.Earthquake Engi⁃neering and Structural Dynamics，2012，41（5）：1043⁃1060.

［4］MARRIOTT D，PAMPANIN S，PALERMO A.Biaxial tes⁃ting of unbonded post⁃tensioned rocking bridge pierswith ex⁃ternal replacable dissipaters［J］.Earthquake Engineering and Structural Dynamics，2011，40（15）：1723⁃1741.

［5］杨浩林，陈卫伟，袁万城.分离式高桩基础承台抗震性能分析［J］.结构工程师，2013，29（4）：89⁃94.YANG Haolin，CHEN Weiwei，YUAN Wancheng.Seismic analysis of a separated pile⁃cap foundation［J］.Structural Engineers，2013，29（4）：89⁃94

［6］HOUSNER G W.The behavior of inverted pendulum struc⁃tures during earthquakes［J］.Bulletin of the Seismological Society of America，1963，53（2）：403⁃417.

［7］ESPINOZA A，MAHIN S.Rocking of bridge piers subjected to multi⁃directional earthquake loading［C］／／8th US Nation⁃al Conference on Earthquake Engineering.［S.l.］，2006.

［8］SAKELLARAKI D，KAWASHIMA K.Effectiveness of seis⁃mic rocking isolation of bridges based on shake table test［C］／／First European Conference on Earthquake Engineer⁃ing and Seismology.Geneva，Switzerland，2006.

［9］HUNG H H，LIU K Y，HO T H，et al.An experimental study on the rocking response of bridge pierswith spread footing foundations［J］.Earthquake Engineering and Structural Dy⁃namics，2011，40（7）：749⁃769.

［10］洪晓慧，张国镇，刘光晏，等.直接基础之摇摆实验与分析［R］.台北：国家地震工程研究中心，2008.

［11］夏修身.铁路高墩抗震设计方法研究［D］.兰州：兰州交通大学，2012：59⁃84.XIA xiushen.Research on seismic design of tall piers for railway bridges［D］.Lanzhou：Lanzhou Jiaotong Universi⁃ty，2012：59⁃84.

［12］周颖，吕西林.摇摆结构及自复位结构研究综述［J］.建筑结构学报，2011，32（9）：1⁃10.ZHOU Ying，LYU Xilin.State⁃of⁃the⁃art on rocking and self⁃centering structures［J］.Journal of Building Struc⁃tures，2011，32（9）：1⁃10.

Finite element modeling methods of aseismic rocking separated pile⁃cap foundation

YANG Haolin，YUAN Wancheng

（State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China）

To propose an alternative seismic strategy，a self⁃centering separated pile⁃cap that could rock under seis⁃mic load in order to cut off the path at the bottom of the foundation of common bridges that energy would transfer was introduced.The principle of this aseismic system is analyzed and multiple tectonic possibilities with feasible construction methods are illustrated.The traditional simulation method for rocking structure treated the rocking con⁃tact surface，i.e.，the rocking foundation as rigid body，ignoring the elastic deformation，which was not quite the case.To optimize this issue，an elaborate finite element model with the rocking area（which is the cap in this pa⁃per）simulated by 3⁃dimensional solid elements is proposed and then compared with traditional modeling method.The analysis in this paper shows that under current bridge seismic design technique and construction technology，aseismic rocking separated pile⁃cap foundation has its possibility in engineering application.Therefore，seeing the rocking area as rigid in FEM methods would conservatively amplify the displacement response of the structure.

separated pile⁃cap；rocking isolation；self⁃centering；seismic design；bridge

10.3969／j.issn.1006⁃7043.201402035

U443.25

：A

：1006⁃7043（2015）06⁃0759⁃06

http：／／www.cnki.net／kcms／detail／23.1390.u.20150428.0851.002.html

2014⁃02⁃27.网络出版时间：2015⁃04⁃28.

国家自然科学基金资助项目（51478339，51278376）；土木工程防灾国家重点实验室基金资助项目（SLDRCE14⁃B⁃14）.

杨浩林（1988⁃），男，博士研究生；袁万城（1962⁃），男，教授，博士生导师.

袁万城，E⁃mail：yuan＠tongji.edu.cn.