水下圆锥壳临界载荷-频率特性分析
李天匀,郭文杰,朱翔,陈忱
(1.华中科技大学船舶与海洋工程学院,湖北武汉430074;2.船舶与海洋水动力湖北省重点实验室,湖北武汉430074)
水下圆锥壳临界载荷-频率特性分析
李天匀1,2,郭文杰1,2,朱翔1,2,陈忱1,2
(1.华中科技大学船舶与海洋工程学院,湖北武汉430074;2.船舶与海洋水动力湖北省重点实验室,湖北武汉430074)
针对基于振动的数值仿真、振动实验预测方法的不足,基于振动的水下圆锥壳临界载荷预报具有结构无损的优势,提出了基于波传播法的水下圆锥壳失稳载荷的理论求解方法。通过建立静水压力下圆锥壳声-固耦合振动方程,并使用波传播法和Galerkin法求解不同静水压下的频率特性。在处理耦合面处流体声载荷时将锥壳分解为多个柱壳微段的流体载荷的叠加。通过对水下圆锥壳的固有频率和静水压力的关系研究,得出静压与固有频率平方近似呈线性关系这一重要结论,并通过线性拟合求出临界载荷。结果对比证实了方法的正确性,且具有简便、计算量小、易于参数优化的优点。
圆锥壳;波传播法;临界载荷;Galerkin法;无损预报
圆锥壳在实际工程中十分常用,比如潜艇的艉段就可以等效看作是圆锥壳。与圆柱壳的几何特性相比,圆锥壳主要特征是横截面半径随母线长度线性变化,这给求解圆锥壳振动特性带来了很大的难度。
水下圆锥壳体的声振特性研究涉及结构动力学、流体力学、声学等多个学科,属于典型的多学科交叉研究领域,其本身具有重要的学术价值。圆锥壳振动特性的研究工作不多,O.E.Crenwelge[1]用能量法计算简支环肋圆锥壳的自由振动Caresta等[2⁃3]用幂级数法求解了流体作用下圆锥壳的动力响应。由于圆锥坐标系下的声波Helmholtz方程目前没有对应的解析解形式,文献[2]在处理声固耦合时采用的是近似方法:将锥壳分解为若干小圆柱壳微段,然后将微段受到的流体声载荷进行叠加。Irie.T[4]用传递矩阵法研究圆锥壳的固有频率,Guo[5]利用多尺度技术研究了流体载荷作用下弹性波在圆锥壳中的传播,曹雄涛等[6]用波传播法求解了正交各向异性锥壳在流场作用下的固有频率。WANG Yongjun等[7]利用幂级数法计算了圆锥壳平衡微分方程的通解,通过构造变形函数利用Galekin法确定特解,从而对静水压力作用下的圆锥壳进行了强度分析。
受压结构稳性的无损检测研究对实际工程问题具有重大的意义,李范春[8]等基于轴压屈曲实验提出了受压结构稳定性的无损检测分析方法,陈忱等[9⁃10]等提出了基于波传播法圆柱壳的临界载荷预报。
本文将静水压力带来的薄膜预应力计及到振动平衡方程中,研究了声固耦合对圆锥壳固有频率的影响,静水压力与固有频率的关系,提出了预测临界载荷理论值的新方法。
1 理论分析
1.1 物理模型
设一截顶锥壳小、大端半径分别R1和R2,壳长L,小端母线方向长度为L1,壳厚为h,半锥角为α,质量密度为ρ;坐标s、θ、z分别代表圆锥壳的母线方向、圆周方向和法线方向,相对应的位移分别为u、v、w;q是静水压力(外压取负值)。
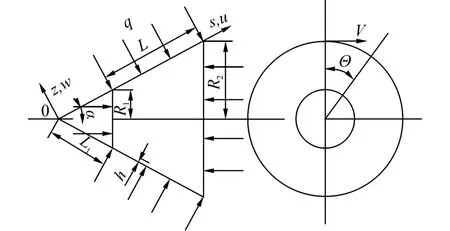
图1 圆锥壳坐标系Fig.1 Coordinate system of conical shell
1.2 壳体方程
根据Flügge壳体理论[11],计及静水压力的平衡方程可以写成如下形式:

式中:F1、F2、F3为轴向、周向和法向载荷,Nθ、Ns、Nsθ、Nθs为单元内面力,为轴向和周向的薄膜预应力,Mθ、Ms、Msθ、Mθs为壳体单元内弯矩,Qθ、Qs为周向、轴向剪力,Pf为流体声载荷,ρ为壳体密度。
根据弹性力学理论,与静水压力q相关的力学分量满足如下物理方程:
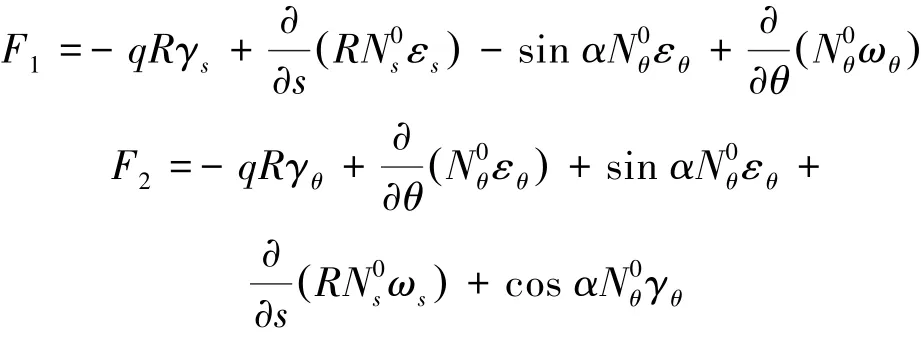

其余各力学分量满足:

式中:E是弹性模量,μ是泊松比,εs、εθ为轴向和周向应变,εsθ为剪应变,χs、χθ为轴向和周向拉伸引起的曲率变化,χsθ为扭转引起的曲率变化。ωs、ωθ、γs、γθ为微元轴向与周向切线绕坐标方向的转角。
1.3 方程的求解
根据曲面的变形协调条件,方程(1)可以简化成如下表达形式:

方程(4)尚无解析解,本文利用Galerkin法近似求解。首先假定一个只满足边界条件而不满足平衡方程的位移型函数。
边界条件为简支且无轴向约束时,在两端有v=w=Ns=Ms=0,满足条件的位移型函数可以设为

式中:n为周向波数,m为轴向振动的波数,U、V、W分别是轴向、周向和法向的广义位移幅值。
将型函数(5)代入方程(4)中可以得到:

然后选取残值函数与权函数,其中式(6)中等式左边的函数可以设为残值函数,权函数与型函数是相似的,只是去掉了广义位移幅值U、V、W。
运用Galerkin法进行积分,采用文献[12]的积分方式,过程如下:

由于该积分表达式很难通过解析积分方式得到结果,所以本文采用数值积分方式。将流体声载荷项分解为多段圆柱壳微段的流体声载荷贡献项的叠加。
柱坐标下理想流体的Helmholtz波动方程:
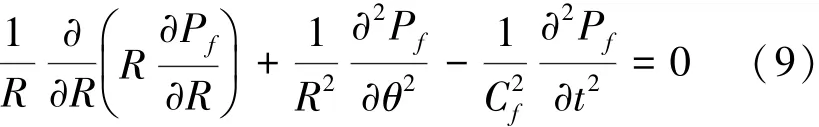
式中:Cf是流体中的声速。
流体与壳体在接触面上必须满足二者径向速度相等:
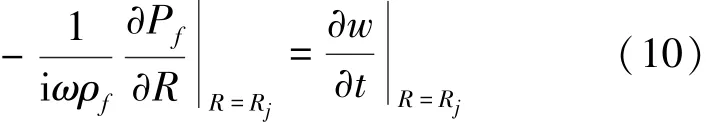
式中:ρf为流体密度,Rj为第j个圆柱壳微段。
采用文献[9⁃10]的处理方法,可由式(9)、(10)解出第j个圆柱壳微段流体声载荷Pf:
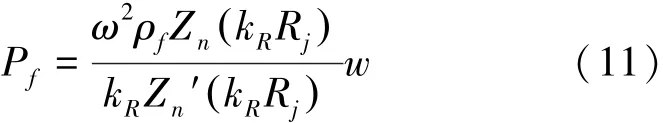
其中流体中压缩波数kf=ω/Cf,结构中轴向波数k= mπ/L,kR2=︱k2-kf2︱。如果kf>k,则Zn()=为第一类汉克尔函数。如果,则()=Kn(),为第二类贝塞尔函数。
此时流体声载荷积分贡献项FL可以表示为叠加形式:
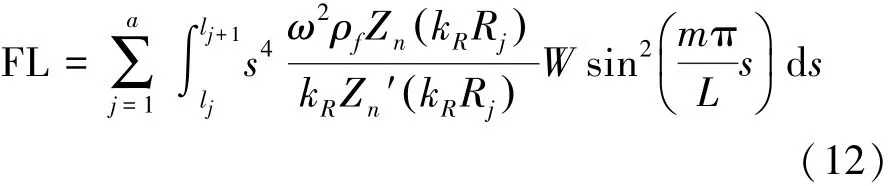
其中将圆锥壳分解为a个小圆柱壳微段,通过计算表明取20个微段时收敛性已经很好,故lj=

式中:Hij的表达式较复杂,限于篇幅本文从略。
2 数值分析
2.1 真空中锥壳自由振动
真空中简支圆锥壳体参数取自文献[10]:h/R2=0.01,μ=0.03,E=2.1×1011Pa,Lsin α/R2=0.25,轴向波数m=1,材料密度ρ=7 850 kg/m3,表中值为无量纲频率

表1 真空中各阶无量纲频率ΩTable 1 Dimensionless frequency Ω of each order in vacuum
本文计算的无量纲频率值和文献[13]对比最大误差不超过2%。验证了方法的可靠性和程序的准确性。
从表1中可以看出圆锥壳结构固有频率的特征:当半锥角一定时,圆锥壳的固有频率随着周向半波数的增加,开始时逐渐下降,然后逐渐上升,取得最小固有频率时的n值不同,如半锥角为30°时,最小固有频率对应的模态为m=1、n=16。当周向半波数n一定时,若周向半波数较小,无量纲频率随半锥角增大而减小;若周向半波数中等,无量纲频率随半锥角增大呈先增后减趋势;若周向半波数偏大,无量纲频率随半锥角增大而增大。
2.2 静水压力与频率的关系
简支壳体参数如下所示:h/R1=0.01,μ=0.03,E=2.1×1011Pa,α=30°,ρ=7 850 kg/m3,ρf=1 000 kg/m3,h=0.01 m,Cf=1 500 m/s,L/R1=2,qcr为临界载荷。
轴向波数m和周向半波数n理论上可以有无穷多种取法,临界载荷值是不同模态下失稳载荷的最小值,在基频处取。故本文需要研究的是基频处模态,当α=30°时,此时的基频模态为m=1、n=16。
从图2中可以看出,静水压力与固有频率的平方近似呈线性关系,而且本文通过计算,发现任意模态(m、n)静水压力与固有频率的平方也会近似呈线性关系。

图2 固有频率与静水压力的关系Fig.2 The relationship between natural frequencies and hydrostatic pressure
圆锥壳失稳时,结构体的刚度丧失,固有频率为零,若能求出频率为零时的静水压力(图3中直线与横轴交点的横坐标),则此压力即可认为是圆锥壳临界载荷的弹性理论解。对图2中的直线进行线性拟合,如图3所示,求出直线与横轴的交点,求得的临界载荷值为0.467 8 MPa。
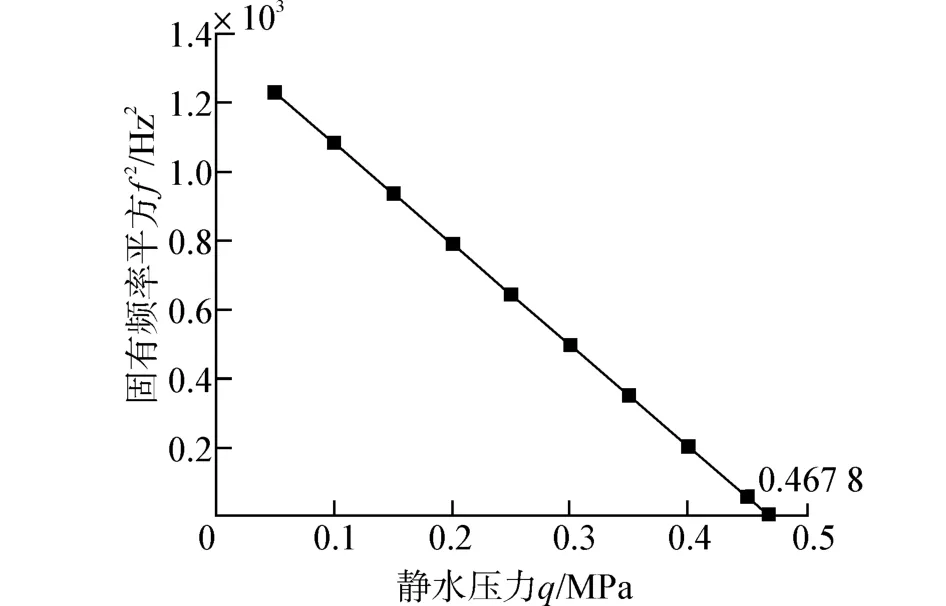
图3 圆锥壳临界载荷的求解Fig.3 Solution of the critical load of conical shell
当半锥角α分别取10°、30°、50°,而其余壳体参数不变时,同理可得圆锥壳的临界载荷。圆锥壳最小的无量纲临界载荷见表2所示(对应轴向波数m=1,括号内的值表示对应的周向半波数n)。

表2 无量纲临界载荷Table 2 Dimensionless critical load
表中文献[12]是基于扁壳理论,而本文采用的是Flügge理论,所以与本文相比存在一定的误差,最大误差小于4%。从表中可以看出在其他条件不变时,临界载荷随锥角增大而显著下降,随壳长变小而显著增大。以上计算得到的是静压下锥壳在两端简支时临界载荷的弹性理论解,要经过几何非线性修正和物理非线性修正[14⁃15],临界载荷值才可运用于工程设计中。
3 结束语
本文提出了基于波传播法的水下圆锥壳失稳载荷的理论预报方法,在建立计及静水压力影响的水下圆锥壳振动方程后,采用Galerkin法计算固有频率。通过线性拟合的方法求出水下圆柱壳临界载荷的弹性理论解。计算结果表明任意模态下的固有频率平方与静水压力成正比,利用固有频率平方与静水压力的线性关系可拟合求出临界载荷,修正后可运用到流体中圆锥类工程结构的临界载荷值的预报。结果对比表明了本文方法的可靠性,为水下圆锥壳临界载荷的无损预报提供了新的方法与思路。
[1]CRENWILGE O E,MUSTER J R D.Free vibration of ring and stringer stiffened conical shells[J].Journal of the A⁃coustical Society of America,1969,46(1):176⁃185.
[2]CARESTA M,KESSISSOGLOU N J.Vibration of fluid load⁃ed conical shells[J].Journal of the Acoustical Society of A⁃merica,2008,124(4):2068⁃2077.
[3]CARESTA M,KESSISSOGLOU N J.Free vibrational char⁃acteristics of isotropic coupled cylindrical⁃conical shells[J].Journal of Sound and Vibration,2010,329(6):733⁃751.
[4]IRIE T,YAMADA G,TANAKA K.Natural frequencies of truncated conical shells[J].Journal of Sound and Vibration,1984,92(3):447⁃453.
[5]GUO Y P.Fluid⁃loading effects on conical shells[J].Jour⁃nal of the Acoustical Society of America,2008,124(4):2068⁃2077.
[6]曹雄涛,华宏星.流体作用下正交各向异性圆锥壳的自由振动[J].振动与冲击,2011,30(11):95⁃100.CAO Xiongtao,HUA Hongxing.Free vibration of orthotropic conical shell interacting with fluid[J].Journal of Vibration and Shock,2011,30(11):95⁃100.
[7]WANG Yongjun,WAN Zhengquan.Strength analysis ofcone shell under hydrostatic pressure[J].Journal of Ship Mechanics,2009,13(6):907⁃914.
[8]李范春,杜玲,刘清风,等.受压结构稳定性的无损检测分析方法研究[J].船舶力学,2010,14(4):393⁃398.LI Fanchun,DU Ling,LIU Qingfeng,et al.No damage tes⁃ting analyzed method research of the compress structure sta⁃bility[J].Journal of Ship Mechanics,2010,14(4):393⁃398.
[9]陈忱,李天匀,朱翔,等.基于波传播法的水下圆柱壳临界载荷-频率特性分析[J].中国造船,2012,53(1):130⁃136.CHEN Chen,LI Tianyun,ZHU Xiang,et al.Frequency characteristics analysis for critical load of a submerged cylin⁃drical shell based on wave propagation approach[J].Ship⁃building of China,2012,53(1):130⁃136.
[10]陈忱,李天匀,朱翔,等.水下环肋圆柱壳弹性失稳临界载荷无损预报方法[J].海洋工程,2014,32(4):89⁃95.CHEN Chen,LI Tianyun,ZHU Xiang,et al.Elastic criti⁃cal pressure prediction of submerged ring⁃stiffened cylindri⁃cal shell based on frequency characteristics analysis[J].The Ocean Engerneering,2014,32(4):89⁃95.
[11]黄克智,夏之熙,薛明德,等.板壳理论[M].北京:清华大学出版社,1987:217⁃223.HUANG Kezhi,XIA Zhixi,XUE Mingde,et al.Theory of Plates and Shells[M].Beijing:Tsinghua University press,1987:217⁃223.
[12]BRUSH D O,ALMROTH B O.Buckling of bars,plates and shells[M].New York:Mc Graw⁃Hill,1975:257⁃270.
[13]LAM K.Y,HUA L.Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell[J].Journal of Sound and Vibration,1999,223(2):171⁃195.
[14]刘涛.大深度潜水器结构分析与设计研究[D].无锡:中国船舶科学研究中心,2001:23⁃75.LIU Tao.Design and analysis of deep sea submersible structures[D].Wuxi:China Ship Scientific Research Cen⁃ter,2001:23⁃75.
[15]刘涛.大深度潜水器耐压壳体弹塑性稳定性简易计算方法[J].中国造船,2001,42(3):9⁃14.LIU Tao.Simplified method of inelastic buckling analysis of deep submersible pressure hull[J].Shipbuilding of China,2001,42(3):9⁃14.
Frequency characteristic analysis of
critical loads for a submerged conical shell
LI Tianyun1,2,GUO Wenjie1,2,ZHU Xiang1,2,CHEN Chen1,2
(1.School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China;2.Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics,Wuhan 430074,China)
In regard to the deficiencies in numerical simulation based on vibration and the method to predict vibra⁃tion experiment,by taking advantage of the prediction for clinical load of vibration-based submerged conical shell that is nondestructive,this paper proposes a theoretical method to solve the collapsing load of a submerged conical shell based on wave propagation approach.It first establishes the acoustic⁃solid coupling vibration equation under the hydrostatic pressure,and solves the frequency characteristics under different hydrostatic pressure by wave prop⁃agation approach and Galerkin method.The data of natural frequencies of the system under different hydrostatic pressures is obtained after solving the coupled equation.Simultaneously,conical shell is divided into several micro⁃sections of cylindrical shells which are superposed when dealing with fluid acoustic loading on the coupling surface.An important conclusion is obtained by the study of relationship between natural frequencies and hydrostatic pres⁃sures,which indicate that there is an approximate linear relationship between squared natural frequencies and hy⁃drostatic pressures.In addition,critical load can be solved by linear fitting.The result obtained from present ap⁃proach is correct,showing good consistency with those from classical theory.Furthermore,present approach has the advantages of simpleness,less calculation and easy to optimize parameter.
conical shell;wave propagation approach;critical load;Galerkin method;nondestructive prediction
10.3969/j.issn.1006⁃7043.201401038
U661.44
:A
:1006⁃7043(2015)06⁃0746⁃05
http://www.cnki.net/kcms/detail/23.1390.u.20150428.0911.014.html
2014⁃01⁃17.网络出版时间:2014⁃04⁃28.
国家自然科学基金资助项目(51379083,51479079);高等学校博士学科点专项科研基金项目(20120142110051).
李天匀(1969⁃),男,教授,博士生导师;郭文杰(1992⁃),男,博士研究生.
郭文杰,E⁃mail:739633869@qq.com

