NA序列部分和之和一阶矩收敛的精确渐近性

邹广玉

NA序列部分和之和一阶矩收敛的精确渐近性

邹广玉

(长春工程学院理学院，吉林长春130012)

随机变量的部分和之和在诸多领域有着广泛应用，关于NA序列的部分和之和取得了许多极限性质.在较弱的矩条件下，利用NA序列部分和之和的渐近分布和二阶矩的稳定性质，得到了平稳NA序列部分和之和的一阶矩收敛的精确渐近性，丰富了NA序列部分和之和极限理论的结果.

NA序列;部分和之和;矩完全收敛性;精确渐近性

定义称随机变量X1，…，Xn是负相伴(NA)的，如果对于{1，…，n}的任意不交子集A、B有，Cov (f1(Xi，i∈A)，f2(Xj，j∈B))≤0，其中f1与f2是任何两个使得协方差存在且对每个变元均非降的函数.

NA序列是包含独立随机变量序列在内的更为广泛的相依随机变量类型，其概念最早由Alam和Saxena［1］提出.NA序列在可靠性理论、渗透性理论及多元统计分析中有重要应用［2］，因此研究其极限性质具有重要意义.

随机变量“部分和之和”的极限理论起源于Resnick［3］和Arnold等［4］对记录值分布的研究，在时间序列分析、随机游动和破产理论等领域中“部分和之和”有着广泛应用.例如:设{Xt，t=0，1，2，…}为随机游动，记，则St可表示第t日的某股票的收盘价，进而便是n日的移动平均线.鉴于部分和之和理论在理论研究和实际应用中的重要性，众多学者对其极限性质进行了研究.文献［5］研究了独立同分布随机变量序列部分和之和的大数定律和中心极限定理，文献［6-7］分别给出了NA序列部分和之和的弱大数定律和中心极限定理，文献［8-9］将其推广至部分和之随机和的弱大数定律，文献［10-11］讨论了独立同分布和NA序列部分和之和的完全收敛性，文献［12］研究了同分布随机变量序列部分和之和的完全收敛性等等.文献［13］给出了NA序列部分和之和的大数定律和重对数律的精确渐近性，本文研究NA序列部分和之和的一阶矩完全收敛性的精确渐近性.

1 主要结论

定理设{Xn，n≥1}为均值为0的严平稳NA随机变量列，且，记

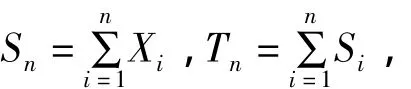
则当0＜p＜r＜2/3时，有

其中:N表示标准正态分布随机变量.

若{Yn，n≥1}为均值为0，方差有限的独立同分布随机变量列，显然满足定理条件，故可得下面的推论.

推论设{Yn，n≥1}为独立同分布随机变量列，满足当0＜p＜r＜2/3时，有

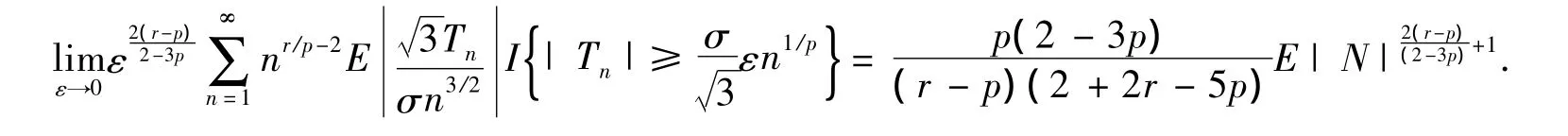
2 2个引理

为证明定理，需要下面2个引理.

引理1［7］设{Xn，n≥1}为均值为0的严平稳NA随机变量序列则

由以上内容可知，高中语文教师在阅读教学中需要坚持核心素养理念。同时，应积极转变传统的教学理念，及时将各种更加高效的教学方式融入阅读教学中。借此措施，增强学生的想象力以及创造力等。

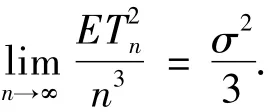
引理2设{Xn，n≥1}为均值为0的严平稳NA随机变量列，且＜∞，记Sn=

3 定理的证明

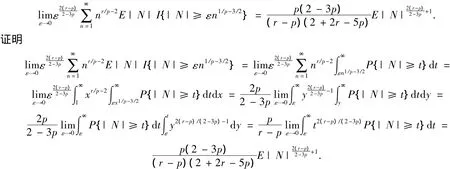
命题2当0＜p＜r＜2/3时，有

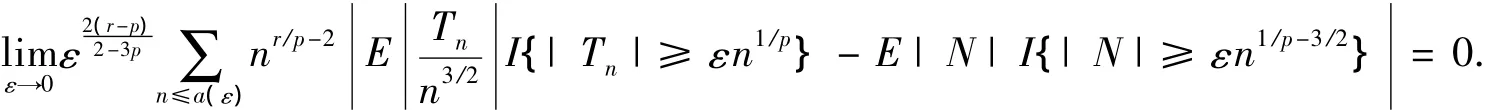
证明

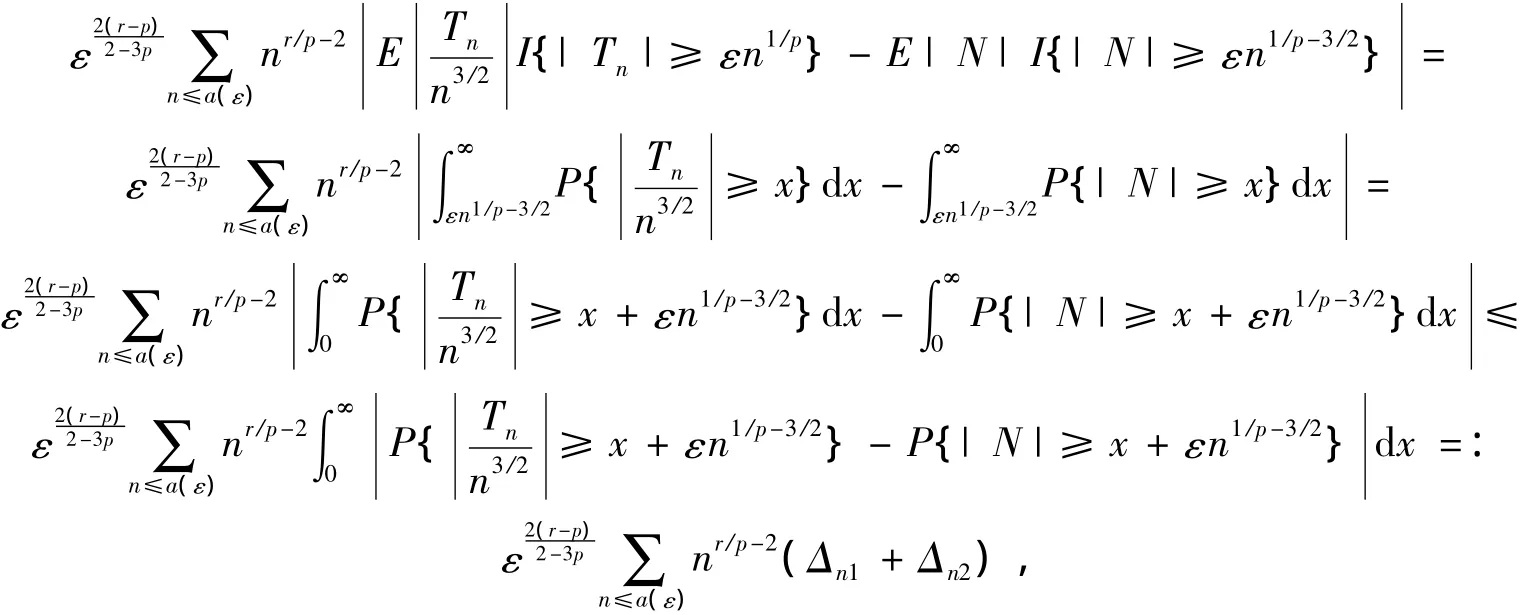
其中:

记Δn=suxp |P{|Tn|≥n3/2x}-P{|N|≥x}|，则由引理2知Δn→0，n→∞，进而由Toeplitz引理［15］，有

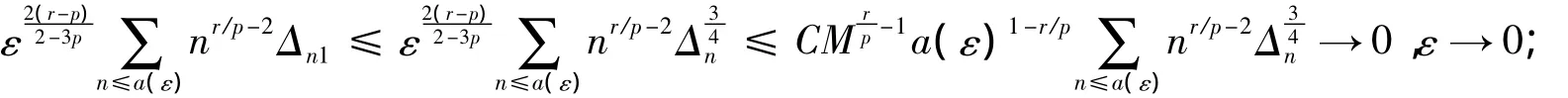
再由引理1可得

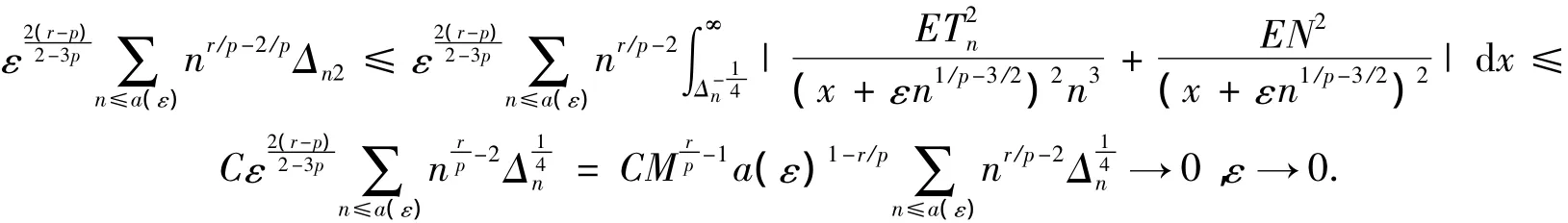
于是命题2得证.

命题3当0＜p＜r＜2/3时，有

证明当0＜p＜r＜2/3时，注意到2r+p＜2，则有r/p-1/p+1/2＜0.结合引理1，有

又

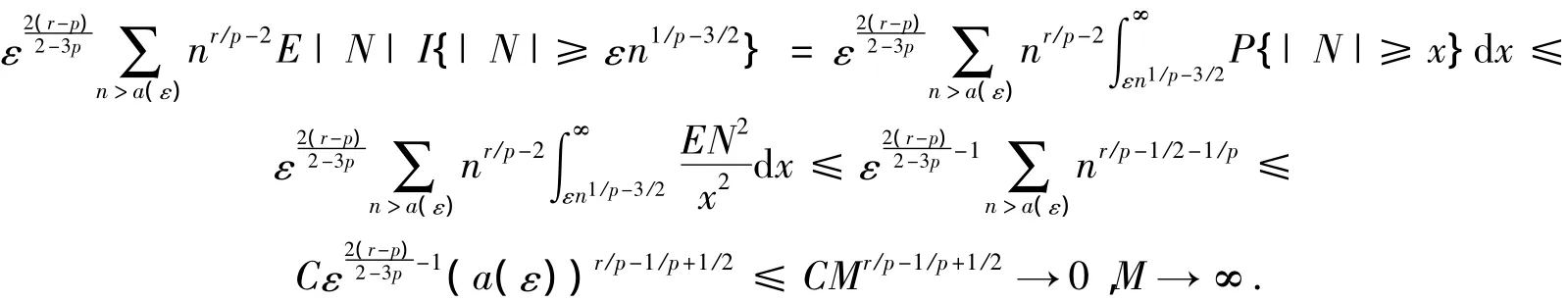
于是命题3成立.

结合命题1～3和三角不等式可知式(1)成立.

［1］Alam K，Saxena K M L.Positive dependence in multivariate distributions［J］.Comm Statist Theory Math，1981，A10(12): 1183-1196.

［2］Roussas G G.Positive and negative dependence with some statistical application［M］//Ghosh S.Asymptotics，Nonparametrices and Time Series.New York:Marcel Dekker，1999:757-788.

［3］Resnick S L.Limit laws for record values［J］.Stochastic Processes and Their Applications，1973，1(1):67-82.

［4］Arnold B C，Villasenor J A.The asymptotic distributions of sums of records［J］.Extremes，1998，1(3):351-363.

［5］江涛，林日其.I.I.D.随机变量部分和之和的极限定理［J］.淮南工业学院学报，2002，22(2):73-75.

［6］宇世航.同分布NA序列部分和之和的弱大数定律［J］.哈尔滨师范大学学报:自然科学版，2004，20(4):21-23.

［7］宇世航，张锐梅.NA序列部分和之和的中心极限定理［J］.高师理科学刊，2007，27(3):1-4.

［8］江涛，林日其.I.I.D.随机变量部分和之随机和的极限定理［J］.中国科学技术大学学报，2001，31(4):394-399.

［9］邹广玉.NA序列部分和之随机和的弱大数定律［J］.长春工程学院学报:自然科学版，2014，15(3):120-122.

［10］兰冲锋，吴群英.I.I.D.序列部分和之和的完全收敛性［J］.吉林大学学报:理学版，2012，50(3):507-510.

［11］兰冲锋，吴群英.NA序列部分和之和的完全收敛性探讨［J］.统计与决策，2013，14:9-11.

［12］兰冲锋，吴群英.随机变量部分和之和的完全收敛性［J］.统计与决策，2014，1:72-75.

［13］邹广玉.NA序列部分和之和的大数定律和重对数律的精确渐近性［J］.吉林大学学报:理学版，2015，53(1):54-58.

［14］张勇，董志山，赵世舜.相依序列加权和的几乎处处中心极限定理［J］.数学物理学报，2009，29(6):1487-1491.

［15］Stout W F.Almost Sure Convengence［M］.New York:Academic Press，1995:120.

Precise Asymptotics in the First Moment Convergence for Sum of Partial Sums of NA Sequences

ZOU Guang-yu
(School of Science，Changchun Institute of Technology，Changchun 130012，China)

The sum of partial sums of random variables is extensively applied in many fields and lots of limit properties are obtained for sum of partial sums of NA sequences.Under weaker moment condition，applying the asymptotic distribution and stable property of second moment for sum of partial sums of NA sequences，we obtain the precise asymptotics in first moment convergence for sum of partial sums of stationary NA sequences，which enriches the results of limit theorem for sum of partial sums of NA sequences.

NA sequence;sum of partial sums;complete moment convergence;precise asymptotics

O211.4

A

(责任编辑 李春梅)

1004-8820(2015)03-0165-04

10.13951/j.cnki.37-1213/n.2015.03.003

2014-09-23

国家自然科学基金资助项目(11401090);吉林省教育厅重点项目(120120113);长春工程学院青年基金项目(320130019).

邹广玉(1982-)，男，吉林通化人，讲师，博士，从事概率极限理论研究.