基于最小均方误差的载频盲估计算法

寻贇贇，赵成林，孟 娟

基于最小均方误差的载频盲估计算法

寻贇贇1，2，赵成林1，2，孟 娟3

（1.北京邮电大学信息与通信工程学院，北京 100876；2.泛网无线通信教育部重点实验室，北京 100876；3.防灾科技学院防灾仪器系，三河 065201）

信号的载频估计在无线电频谱资源的使用和管理中起到了至关重要的作用。现有的载频估计算法载估计精度，计算复杂度等方面均存在严重不足，不利于仪表应用。结合典型的谱重心法和最小均方误差算法的特点，提出了一种新的载频盲估计算法。该算法无须知道信号的体制类型，即可对信号直接进行载频估计。该算法以谱重心法得到的载频估计值为粗估计，并利用平滑后的功率谱中间段对称性更好的特性，根据最小均方误差算法计算粗估计误差范围内的局部对称性大小，求取对称性最好的位置作为载频精估计值。在高斯信道下的仿真实验结果表明：相比谱重心法，新算法的估计精度在不同信噪比下均有较大的提高。特别是在低信噪比的情况下，载频估计的精度提升更明显。因此，新算法在无线频谱监测中有着很好的应用前景。

载波频率；盲估计；谱重心法；最小均方误差算法；频谱资源监测

0 引 言

载频估计在民用信号的频谱利用情况的监管上起着相当重要的作用，国家无线电监管部门为保证合法频率信号的正常通信，就必须能够识别和防止非法信号频率的干扰。为了达到这个目标，就需要对不同体系下的信号进行载频估计来判断信号是否在合法的频段上。因此，需要一种高精度地载频估计方法来达到更好得频谱监管。

对于载频估计，现有已有很多相关的估计算法。文献［1］根据信号单位时间内过零点的次数来估计信号的载频，但是信号受噪声影响，在接近零点的位置容易发生跳变；使着这种估计算法得到的载频估计不准确。文献［2］根据信号功率谱的重心所在位置估计信号的载频，这种算法实现简单，但是估计精度很低，特别是在低信噪比条件下。根据有些调制信号的功率谱在载频位置的峰值特征，通过估计信号的功率谱峰值来估计信号的载频的周期图法，但是这种算法只适合部分信号，而对于大多数无线通信系统信号来说并不适合。文献［3，4，5］通过对信号进行自相关运算，将载波频率估计转化为相位差分问题，提出一种相位差分法；但是由于这种方法也是一种时域的载频估计算法，受噪声影响比较大，得到的估计精度不高。文献［6，7］根据不同调制方式下信号的循环功率谱在载频位置上的谱特性来估计载频，但是对于不同的调制方式下，估计方式不同，需要已知信号的调制方式才能进行准确的载频估计。文献［8］根据信号的高阶统计量来估计信号的载频，由于高阶统计量的运算复杂很高，并不适合工程实现。文献［9，10］用不同的方法对MPSK进行了载频盲估计，但是只适用于MPSK信号。文献［11］根据信号的M次方会在M倍信号载频处出现离散谱线来估计信号的载频，但是这种方法要已知信号的调制方式。

本文提出了一种基于最小均方误差算法的载频估计算法，在谱重心法的基础上，结合了最小均方误差算法，选取局部搜索范围内信号对称性最好的点作为信号的载频估计值的精估计算法。为了检验算法对于不同体制信号均有较好的适应性，本文选取了载频和带宽相差较大的GSM、WCDMA、LTE三种体制下信号分别进行仿真实验。

1 系统模型

不同模式下信号在基带调制之后均可以分为I（t）、Q（t）两路信号，可以用如下公式表示：

其中，I（t）代表基带调制信号的同相分量；Q（t）代表基带调制信号的正交分量；fs为基带信号的频率；A（t）为基带信号的幅度随时间变化的函数。信号通过载频调制后的信号模型为：

其中，fc为载波频率大小。

经过高斯白噪声信道后的接收信号r（t）表示为：

其中，n（t）代表高斯白噪声的大小。

本文中载频盲估计就是估计接收信号中fc的大小。思路为先根据谱重心法求得信号的载频粗估计值，然后根据粗估计的结果，根据最小均方误差算法求得信号的载频精估计值。

2 谱重心法

谱重心法就是根据信号的功率谱的对称性，通过求信号的功率谱的重心所在的频点位置作为信号载波频率的估计值的一种方法。由于不同体制的信号的功率谱均具有对称性；因此，谱重心法是一种通用的载波频率的方法。

根据参考论文［2］知，对于谱重心法的估计表达式为：

其中，R（k）为通过对接收信号进行功率谱估计得到的功率谱序列，因此功率谱估计的精度直接影响载频估计的精度。为了能得到较好的信号的功率谱特征来进行谱重心法进行载频估计。采样率和真实载波频率至少要满足公式：

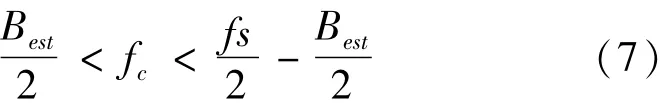
其中Best为信号载频估计所用频段宽度。

通过上面的谱重心法求信号功率谱的公式可以看出，此算法计算公式非常简单，只需要求出信号的功率谱带入公式就可以实现载频估计。但是要想实现算法的精确估计，本文在谱重心法的基础上做了一系列的改进。

3 基于最小均方误差算法的高精度载频盲估计算法

由于上面提到的谱重心法估计精度低，且低信噪比下估计不准确的问题。本文提出的载频盲估计方法分为两个步骤，首先，对接收信号进行预处理，通过去噪和更精确的功率谱估计来提升载频粗估计的精度。然后，对信号进行谱重心法估计，得到信号载频粗估计值，最后再对信号基于最小均方误差算法进行载频精估计，对粗估计结果做进一步修正。

3.1信号预处理

由于功率谱的分辨率可以直接影响载频估计的精度，只有在保证频率分辨率的前提下，才可以通过功率谱特征来得到更精确的载频估计值。即应该先选择合适的算法对接收信号进行功率谱估计，来提高功率谱估计的频率分辨率。由于信号的载频估计还要受噪声的影响，本文通过对信号功率谱进行平滑处理来减小信号噪声的影响和更好地选择信号门限，来提升信号粗估计的精度。

3.1.1功率谱估计

谱重心法下信号载频估计的前提是需要估计信号的功率谱；功率谱估计是对信号进行分析的有效工具。目前，主要的功率谱估计方法主要有周期图法、自相关法、welch谱估计法。其中，周期图法是最简单的谱估计方法，直接取傅里叶变化后再进行平方即可得到；可以通过FFT运算得到，运算量最低，信号变化幅度较大，分辨率较高。自相关法为根据功率谱原理得到的估计方法，先进行自相关运算，再进行傅里叶变换得到，由于要经过自相关，运算量比周期图法要大，得到的结果与周期图法相似，同样是信号变化幅度较大。Welch谱估计法，先将数据分成K段，可独立或者重叠，即k=N/L或者k=（NL/2）/（L/2）（重叠一半）。再把每段数据乘以窗函数w（n）后作傅里叶变换，信号较平滑，但分辨率较低。

影响精度提高的因素主要为功率谱分辨率：

其中fs为信号的采样率，N为信号的数据长度。即在采样率一定的情况下，信号的数据长度越长，信号的功率谱分辨率越高。由于载频估计要求功率谱估计要有较高的功率谱分辨率和较低的运算量，考虑到这两个因素，我们选择周期图法进行谱估计。

3.1.2功率谱平滑

由于信号的功率谱的两端拖尾部分幅度趋近于零，在信噪比较小的情况下受噪声影响明显，导致载频估计误差增大［12］。而且如果两端拖尾长度选取位置不对称的话，在求取信号功率谱的重心时必然造成向信号长拖尾的一边偏移，从而增大了信号的载频估计误差。因此，选择合适的阈值算法来去掉信号功率谱两边受噪声影响比较大的拖尾，仅对功率谱中间的频率段内的数据进行载频估计，会使载频估计的精度大大提高。

由于周期图法得到的信号的功率谱变化幅度较大，可采用频域加窗平滑的方法来对信号进行平滑，来减小信号功率谱变化幅度，以更好地通过阈值找到功率谱两边的对称位置，以便提高谱重心法的估计精度。

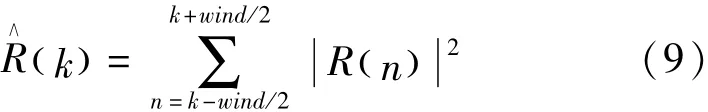
本文中所采用的频域窗为简单的矩形窗，加窗公式如下所示：其中，R（n）为信号平滑前的功率谱；R∧（k）为信号平滑后的功率谱；wind为信号平滑窗的大小。本文通过增加一个窗后的数据和减少一个窗前数据来计算频率移动之后的来计算平滑后的功率谱的方式，来大大减少算法运算量。得到信号平滑之后的功率谱之后，我们选取信号0.15倍的最大值来作为信号载频估计频段的阈值，在阈值以内求取信号的功率谱的重心位置作为载频粗估计结果，可减小功率谱拖尾造成的载频估计误差。

3.2最小均方误差算法精估计算法

本文对最初的谱重心法从功率谱的计算和功率谱平滑两个方面进行了改进，来得到信号的载频粗估计值，并在此粗估计结果的基础上，对信号载频估计结果进一步修正，提出了一种基于最小均方误差算法的精估计算法。

3.2.1基本原理

根据不同体制信号的功率谱关于载频的对称性，将粗估计的结果的载频中心的位置作为参照中心，向左向右移动其位置，滑动窗大小为2倍的最大粗估计误差Δfe，来尽可能的修正粗估计误差。寻找对称性最佳的位置所在的中心频率的位置来作为信号精估计值。

根据最小均方误差算法的公式为：

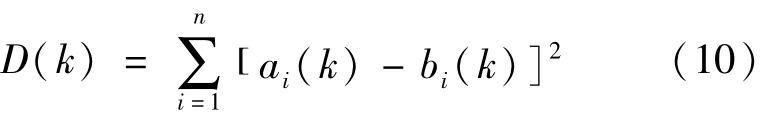
可以计算信号功率谱的两边对应位置的对称性大小。根据公式可知，最后得到的D（k）的值越小，说明信号的对称性越好。因为通过得到的D（k）曲线，求取曲线的最小值即为信号对称性最好的位置，即载频精估计的大小。

3.2.2算法步骤

（1）根据谱重心法粗估计结果f′c为载频中心位置f，计算出功率谱最大值Rmax，根据不同体制信号的功率谱图分析得到，在功率谱幅度在上升过程中信号的对称性更好，如图1所示。在不同频率段信号受噪声影响的效果大小相同，因此，在功率谱幅度值较小的位置，信号受噪声的影响相对大。在功率谱幅度较大的频率段，信号受噪声的影响相对较小，但这段信号的波动幅度比较大，即使偏移一个点都会对结果造成很大影响。考虑到这些因素，经过多次仿真实验，选取信号的功率谱为0.45Rmax到0.7 Rmax的频率段作为载频估计段。

图1 不同体制信号的功率谱图

（2）找到f的功率谱左半边的幅度为0.45Rmax到0.7 Rmax横坐标所在位置f1和f2，在f1和fn之间均匀的取点f2、f3、f4……fn-1；根据这些点到f的距离，在f的右边取点。得到对应的f1′、f2′、f3′…….fn′。

（3）根据上面公式（10），采用此最小均方误差算法，可得：

改变频率f的值的大小，范围为（-Δfe+fc′，Δfe+fc)′，间隔为功率谱分辨率Δf，得到关于f的函数D（f）。

（4）根据曲线D（f），通过搜索曲线最小值的方法，可以得到修正后的载波频率精估计值。在谱重心法的基础上，经过上面的四个步骤，即可实现信号载频精估计。

4 仿真实现与性能分析

4.1仿真条件

由于论文主要讨论在不同体制下信号的载频估计的性能优劣，为了更全面地分析算法的性能，本文选取了LTE、WCDMA、GSM三种特征比较明显的信号进行仿真实现。参考不同体制信号的标准可得知信号的一些仿真参数，来设置本文的仿真环境如下：

为保证采样率和真实载波频率要满足的公式（7）。可知只有采样率足够大，才能保证可以得到有效的功率谱来进行载频估计。根据频率分辨率的公式（8），知当信号的采样率过大时，又会导致信号功率谱的频率分辨率过小，从而影响载频估计的精度。考虑上面两个因素，我们选取信号的数据长度为N=4.334×106，在高斯白噪声信道条件下，通过在载频估计归一化误差均值和方差来评价算法性能。归一化平均误差曲线NME和归一化均方误差曲线NMSE公式为（12）和（13）

蒙特卡洛实验次数。

4.2仿真结果

本文在不同信噪比下，分别对三种信号体制进行了仿真，通过比较不同体制信号在谱重心法和新算法下得到载频估计的误差均值来验证新算法的估计精度和有效性，及误差方差来验证新算法的估计稳定性。下面是具体的仿真结果分析：

（1）在不同信噪比下，通过200次蒙特卡洛实验得到的两种载频估计方法的误差均值如图2所示。

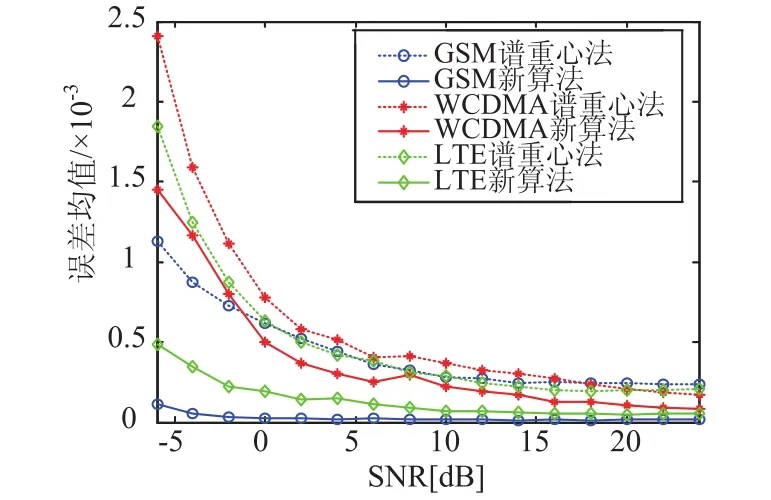
图2 不同信噪比下两种算法的误差均值曲线

通过图2可以看出基于最小均方误差算法的盲估计算法对于三种体制下的信号在不同的信噪比条件下均可降低载频估计误差，说明通过最小均方误差算法来局部搜索可实现载频估计的修正。特别是当信噪比较小的情况下，传统的频率重心法得到的载频粗估计的误差较大，但对于改进后的基于最小均方误差算法的载频盲估计算法，由于通过功率谱平滑来去噪及选择受噪声较小的谱段来局部搜索等实现对低信噪比的处理，来更好的修正其误差，获得比较好的估计性能；即通过仿真验证了本文提出算法的有效性和准确性。

（2）在不同信噪比下，通过200次蒙特卡洛实验得到的两种载频估计方法的误差方差如图3所示。

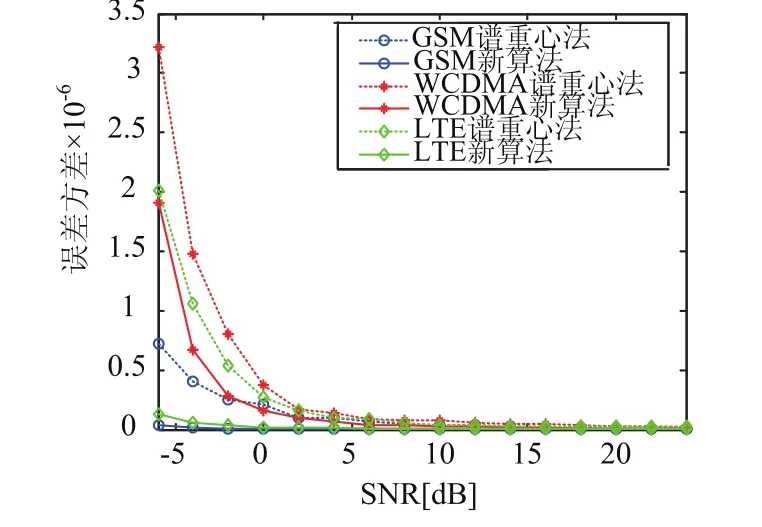
图3 不同信噪比下两种算法的误差方差曲线

通过图3可以看出本文提出的盲估计算法在不同信噪比下的估计误差方差更小，也就是说，改进的载频盲估计算法稳定性更佳。在信道环境恶劣的情况下，性能提升效果更加显著。

综上所述，可以看出新算法在估计精度和估计的稳定性上相比谱重心法都有较大的提升，由于对于不同的信噪比下估计性能都很好，即对加性高斯白噪声信道着很好的适应性。因此，本算法是一种适应性强、精度高、稳定性好、且基本不需要先验知识的一种载频盲估计方案。

5 结束语

本文通过最小均方误差算法来计算信号的对称性，并利用信号在功率谱谱幅度的中间段对称性较好的特性，在原谱重心法的基础上，对信号的载频估计值进行进一步的修正。通过计算修正曲线的最小值的方法来重新定位载频位置。通过MATLAB仿真实验表明，这种方法对于不同体制的信号均有很好的估计性能提升。由于本算法无须知道信号体制等先验知识就可以较为精确地估计出信号载频，特别适用于现在多种信号体制并存环境下无线电频谱监测和管理。

［1］ Hsue SZ，Soliman SS.Automaticmodulation classification using zero crossing［J］.Iee Proceedings F，1990，137（6）：459-464.

［2］ Baarrij SM，Nasir F，Masood S.A Robust Hierarchical Digital Modulation Classification Technique：using Linear Approximations［C］//2012 IEEE International Symposium on Signal Processing and Information Technology（ISSPIT）IEEE，2006：545-550.

［3］ Volker B，Handel P.Frequency estimation from proper sets of correlations［J］.Signal Processing IEEE Transactions on，2002，50（4）：791-802.

［4］ Zhang L，Wang J.A Fast Blind Carrier Frequency Estimation Algorithm for Digitally Modulated Signals［C］// Wireless Communications Networking and Mobile Computing（WiCOM），2010 6th International Conference on-IEEE，2010：1-3.

［5］ 张路平.数字通信信号的调制方式识别与参数估计［D］.南京：南京理工大学，2012.

［6］ Gardner W A，Robinson E A.Statistical spectral analysis：a nonprobabilistic theory［J］.Journal of Dynamic Systems Measurement&Control，1990，29（4）：673.

［7］ GardnerW/，Brown W/I，Chen C K.Spectral Correlation of Modulated Signals：Part II—Digital Modulation［J］.IEEE Transactions on Communications，1987，35（6）：595-601.

［8］ Swami A，Sadler B M.Hierarchical digital modulation classification using cumulants［C］//IEEE Trans.Commun.，vol2000：416-429.

［9］ 苑小华，罗武忠，罗来源.MPSK信号载波频率盲估计［J］.电子与信息学报，2008，30（5）：1148-1150.

［10］邓振淼，刘渝.MPSK信号载频盲估计［J］.通信学报，2007，28（2）：94-100.

［11］郑文秀.数字通信信号的参数估计与干扰技术研究［D］.西安：西安电子科技大学，2008.

［12］王戈，严俊.一种基于功率谱估计的盲载频估计新算法［J］.计算机工程与应用，2012，48（13）：114-117.

A Blind Frequency Estimation Algorithm Based on Least Mean Square

XUN Yun-yun，ZHAO Cheng-lin，MENG Juan
（1.Beijing University of Posts and Telecommunications，Department of Communication and Information System，Beijing 100876，China；2.Key Laboratory of University Wireless Communications，Ministry of Education，Beijing 100876，China；3.Department of Disaster Prevention Instrument，Institute of Disaster Prevention，Sanhe 065201，china）

Carrier frequency estimation plays a role in the supervision and management of radio spectrum resources.The currentmethods of carrier frequency estimation algorithm has some disadvantages，such as，frequencymediacymethod with low accuracy and cyclic spectral correlation algorithm with high complexity.In order to improve estimated accuracy，a new blindmethod based on frequencymediacymethod and leasemean squaremethod is proposed to estimate signal carrier frequency.This algorithm can estimate carrier frequency of

signal and require no priori knowledge about the type of signal.This method on the basis of frequencymediacy algorithm as rough estimate result，then bymeans of the better symmetry of smoothing power spectrum on themiddle frequency band and leasemean square algorithm to compute the symmetry on the range of rough estimated deviate，and select the best point of symmetry as the final estimated result.The simulation results show that the new algorithm has high accuracy rather than frequencymediacymethod at AWGN environment，especially at low Signal to Noise Radio（SNR）. Therefore，the new method canmore accurately detect themutual occupation situation of the spectrum resources.It has a better prospect in the supervision ofwireless spectrum resources.

carrier frequency；blind estimation；frequencymediacymethod；leasemean squaremethod；the supervision of radio spectrum resources

TN911

：A

：1673-5692（2015）06-574-05

寻贇贇（1990—），山东济宁人，硕士研究生，主要研究方向为无线通信信号处理新技术；

E-mail：xunyunyun1990@163.com

赵成林（1965—），北京人，教授，主要研究方向为信号处理、参数估计、无线传感器网络；

孟 娟（1983—），湖南南县人，讲师，主要研究方向为宽带无线通信。

10.3969/j.issn.1673-5692.2015.06.003

2015-10-09

2015-11-12

国家科技重大专项（2014ZX03001027）