带有反应扩散项的食饵-捕食系统的Hopf分支
张建强,张 旻,邵瑞锋
(兰州交通大学 数理与软件工程学院,兰州 730070)
带有反应扩散项的食饵-捕食系统的Hopf分支
张建强,张 旻,邵瑞锋
(兰州交通大学 数理与软件工程学院,兰州 730070)
研究了带有反应扩散项和比率依赖功能反应函数的Holling-Tanner食饵-捕食系统的Hopf分支, 分支方向以及分支周期解的稳定性.
比率依赖功能反应函数;Holling-Tanner食饵-捕食系统;Hopf分支
在文献[1]中,May提出了Holling-Tanner食饵-捕食系统.就生态学来讲,该系统可以用来描述麻雀和食雀鹰等生态系统中种群间的相互作用[2-3],因此受到了广泛的关注.
Holliing-Tanner 食饵-捕食系统如下:
(1)
其中,U(x,t)和 V(x,t) 分别代表食饵和捕食者在t时刻的种群密度;R和H分别代表内禀增长率;K为食饵的最大环境容纳量;U/C为捕食者依赖于食物的容纳量;1/C可以表示食饵转化为捕食者食物的转化率 M代表单位时间内单位捕食者消耗食饵的最大数量;D代表1/C达到一半时对应于食饵的饱和率.
Holliing-Tanner食饵-捕食系统具有丰富的动力学行为,比如正常数平衡解的全局稳定性,周期解,稳定的极限环,半稳定的极限环等[2-3].在大多数情况下,当食饵捕食理论建立在所谓的比率依赖理论上时更符合实际情况.比率依赖系统如下
(2)
还有一种情况我们应当考虑,如果种群在空间上是非均匀分布的,且栖息在固定的有界区域Ω∈Rn,我们就可以得到以下反应扩散系统
(3)
其中Δ表示Laplace算子;D1,D2分别表示食饵和捕食者的反应扩散系数; 边界条件为齐次Neumann边界条件,这说明系统 (3) 是自封闭的,食饵和捕食者都离不开栖息地.对于带有反应扩散项的Holliing-Tanner食饵-捕食系统已有很多的研究,例如它的全局稳定性,Hopf分支,稳态分支等[7-8].对于带有反应扩散项和比率依赖功能反应函数的食饵-捕食系统也有很多的研究,例如全局稳定性以及局部稳定性等.
本文主要利用文献[4]中的方法,在定义的Sobolev空间中将无穷维算子的特征值问题转化为可列个矩阵的特征值问题,通过分析线性化算子的特征值,以及中心流行和规范型理论.得到了系统(5)的空间齐次和非齐次周期解的Hopf分支值,并且推导出了系统空间齐次Hopf分支值的分支方向和稳定性条件.
1 带有反应扩散系统的空间齐次和非齐次Hopf分支值
对系统 (3) 做无量纲化变换. 令
我们仍然用t代表s,得到与系统 (3) 等价的以下系统
(4)
为了后面讨论的方便以及得到更好的结果,我们假设空间Ω=(0,lπ),l∈R+,是空间一维的.并且由[5],我们可以假设d1=1,d2=1, 并且通过选择适当的比例使a=1,
接下来为了讨论系统(4)间齐次和非齐次Hopf分叉的存在性,我们固定参数h,让λ作为分支参数.

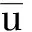
(5)
这就将系统 (4)价的转化为系统 (5)的(0,0) 解.
定义实的Sobolev空间为
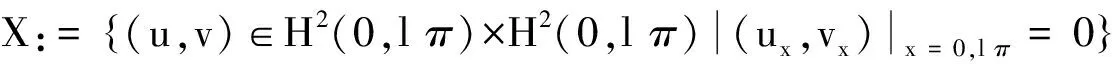
同时定义X复化空间为
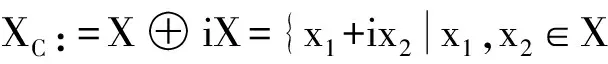
可得系统 (5)在(0,0)点的线性化算子为
(6)
众所周知
-ψ″=γψ,x∈(0,lπ),ψ′(0)=ψ′(lπ)=0.
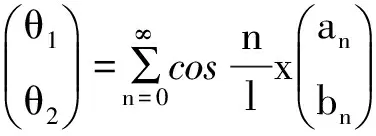
为L(λ) 对应的特征值 γ(λ) 的特征函数,也就是L(λ)(θ1,θ2)T=γ(λ)(θ1,θ2)T. 通过分析可得

其中

由此可知,L(λ) 的特征值可以由 Ln(λ) 的特征值给出,其中n∈N0,Ln(λ) 的特征方程为
μ2-μTn(λ)+Dn(λ)=0,n∈N0,
其中
(7)
因此,特征值为

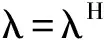
下面将考虑系统可能发生Hopf分支的分支值λH.从而存在n∈N0使得
Tn(λH)=0,Dn(λH)>0, 对m≠n满足Tm(λH)≠0,Dm(λH)≠0,
(8)
并且在唯一的一对纯虚根α(λ)±iω(λ)附近满足α′(λ)≠0.
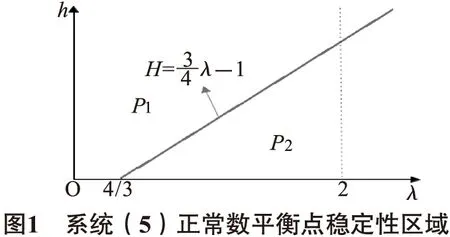
其中,
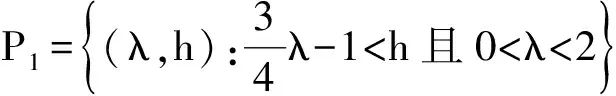
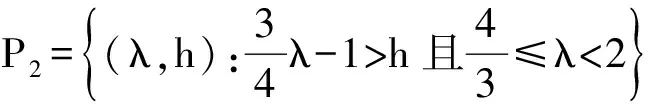

从而,可能发生Hopf分支的任何分支值一定在区间[λ*,2),对区间[λ*,2)它的任一Hopf分支值λH,α(λH)±iω(λH)是L(λ)的特征值.则

并且
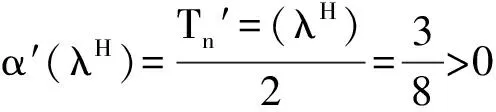
(9)
根据以上分析,我们可以用以下集合来考虑Hopf分支值问题
ΛH:={λH∈[λ*,2):对于某个 n∈N0,(9)式成立}.
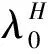
定义
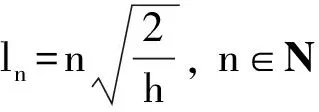
(10)


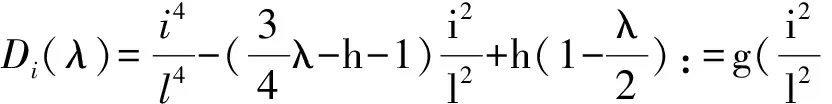
(11)

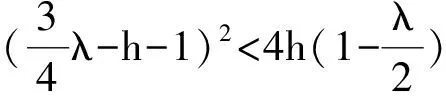
通过以上分析,我们得到以下结论.
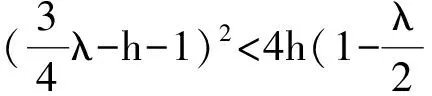

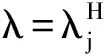
2 带有反应扩散系统的空间齐次周期解的分支方向和稳定性
证明:以下证明主要采用文献[7]中的标记. 记

系统(5)在正常数平衡点E*=(u*,v*)处可以写成以下形式

其中


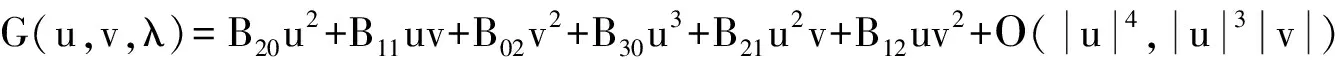
其中
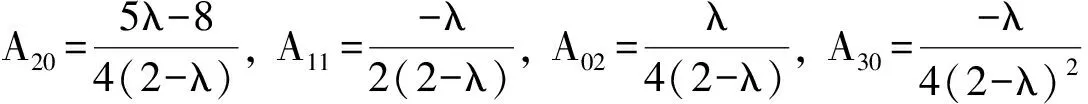
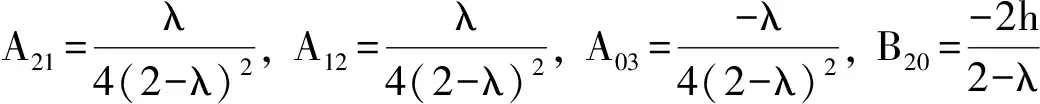

从而可得
c0:=C1+C2iω0, d0:=D1+D2iω0, e0:=E1+E2iω0,
f0:=F1+F2iω0, g0:==G1+G2iω0, h0:=H1+H2iω0.
其中


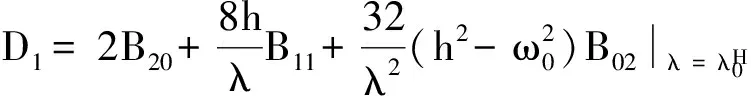
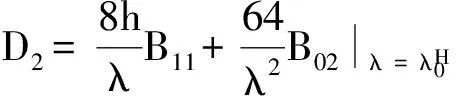

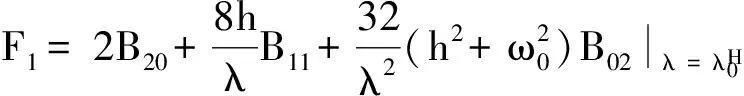


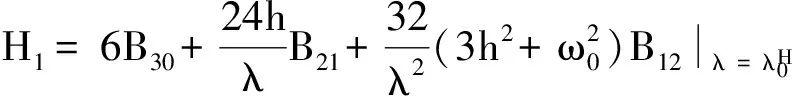

则

因此




由此计算可得H20=0, H11=0.

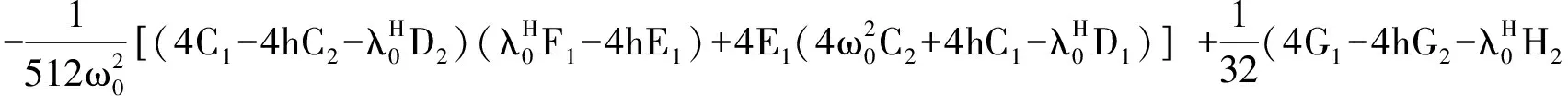
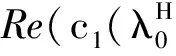
[1] SáEZ E, GONZáLEZ-OLIVARES E. Dynamics of a predator-prey model[J]. SIAM Journal on Applied Mathematics, 1999, 59(5):1867-1878.
[2] TANNER J T. The stability and the intrinsic growth rates of prey and predator populations[J]. Ecology, 1975:855-867.
[3] WOLLKIND D J, COLLINGS J B, LOGAN J A. Metastability in a temperature-dependent model system for predator-prey mite outbreak interactions on fruit trees[J]. Bulletin of Mathematical Biology, 1988, 50(4):379-409.
[4] YI Feng-qi, WEI Jun-jie, SHI Jun-ping. Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system[J]. Journal of Differential Equations, 2009, 246(5):1944-1977.
[5] DU Y, HSU S B. A diffusive predator-prey model in heterogeneous environment[J]. Journal of Differential Equations, 2004, 203(2):331-364.
[6] PENG R, WANG M. Positive steady states of the Holling-Tanner prey-predator model with diffusion[J]. Proceedings of the Royal Society of Edinburgh:Section A Mathematics, 2005, 135(1):149-164.
[7] CHEN S, SHI J. Global stability in a diffusive Holling-Tanner predator-prey model[J]. Applied Mathematics Letters, 2012, 25(3):614-618.
[8] LI Xing, JIANG Wei-hua, SHI Jun-ping. Hopf bifurcation and Turing instability in the reaction-diffusion Holling-Tanner predator-prey model[J]. IMA Journal of Applied Mathematics, 2013, 78(2):287-306.
(责任编辑 梁志茂)
Hopf bifurcation in the reaction-diffusion prey-predator system
ZHANG Jian-qiang,ZHANG Min,SHAO Rui-feng
(School of Mathematics, Physics, and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
The Hopf bifurcation of Holling-Tanner prey-predator system which contains reaction-diffusion and ratio-dependent functional response,the bifurcation direction and the bifurcation periodical stability ate studied.
ratio-dependent functional;Holling-Tanner prey-predator system;Hopf bifurcation
2014-09-29.
张建强(1986-),男,硕士研究生.主要研究方向:非线性动力学与模拟控制.
O175.13
A
1672-8513(2015)04-0304-06

