关于“依测度收敛”概念教法的探究
崔 颖
阜阳师范学院数学与统计学院,安徽阜阳,236041
关于“依测度收敛”概念教法的探究
崔 颖
阜阳师范学院数学与统计学院,安徽阜阳,236041
依测度收敛这一概念使集合的测度与极限交混在一起,变得非常抽象而不易理解。为了使这一抽象概念形象具体,在依测度收敛概念的教学中可以运用构造法、形象法及转化法,通过构造处处不收敛的特殊函数列引出依测度收敛的定义,并且运用函数图像和点集的特征刻画了依测度收敛的几何意义,从而使抽象的依测度收敛概念形象化,运用这一几何意义可快速判断一些函数列是否依测度收敛。同时,又借助函数列的依测度收敛与几乎处处收敛之间的相互转换,不需要用精细的测度论方法便可简捷地将普通收敛的唯一性与连续性推广到依测度收敛。
依测度收敛;构造法;形象法;转化法
实变函数论涉及的概念不仅多且许多数学符号、概念和定理交织在一起,这让初学者很难正确理解这些抽象的定义与定理。为了提高学生的学习兴趣,笔者采用不同的教学方法来提高实变函数的教学效果。例如,运用类比建构的方法,使学生掌握Lebesgue测度理论[3];通过介绍某些概念的历史背景,使学生理解引入一些概念的必要性[4];借助形象思维的例子,将抽象的数学问题形象化[5]。
依测度收敛是实变函数中较为抽象的概念,初学者不易理解这一概念及相关性质,从而对有些依
测度收敛问题的讨论束手无策。然而,依测度收敛不仅在实变函数而且在概率论中,都有重要应用。于是,使学生正确理解并应用这一概念是非常必要的。本文运用构造法、形象法及转化法,分别探讨依测度收敛概念的教学。
1 构造法引出概念
学生在学习实变函数之前,主要讨论函数列的收敛及一致收敛。为了引出依测度收敛这一抽象概念,可以构造如下函数列。
例1 对给定的自然数n,总可以找到唯一的自然数k与i,使n=2k+i(0≤i≤2k,k=1,2,…)[6]。
现构造区间(0,1]上的函数列
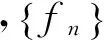



2 形象法理解定义
依测度收敛是通过可测集测度的极限是否为零定义的,但可以借助函数图像及点集的特征有效理解这一概念。
由于定义1中的可测集E[|fn-f|≥σ]的补集为:
E[|fn-f|<σ]
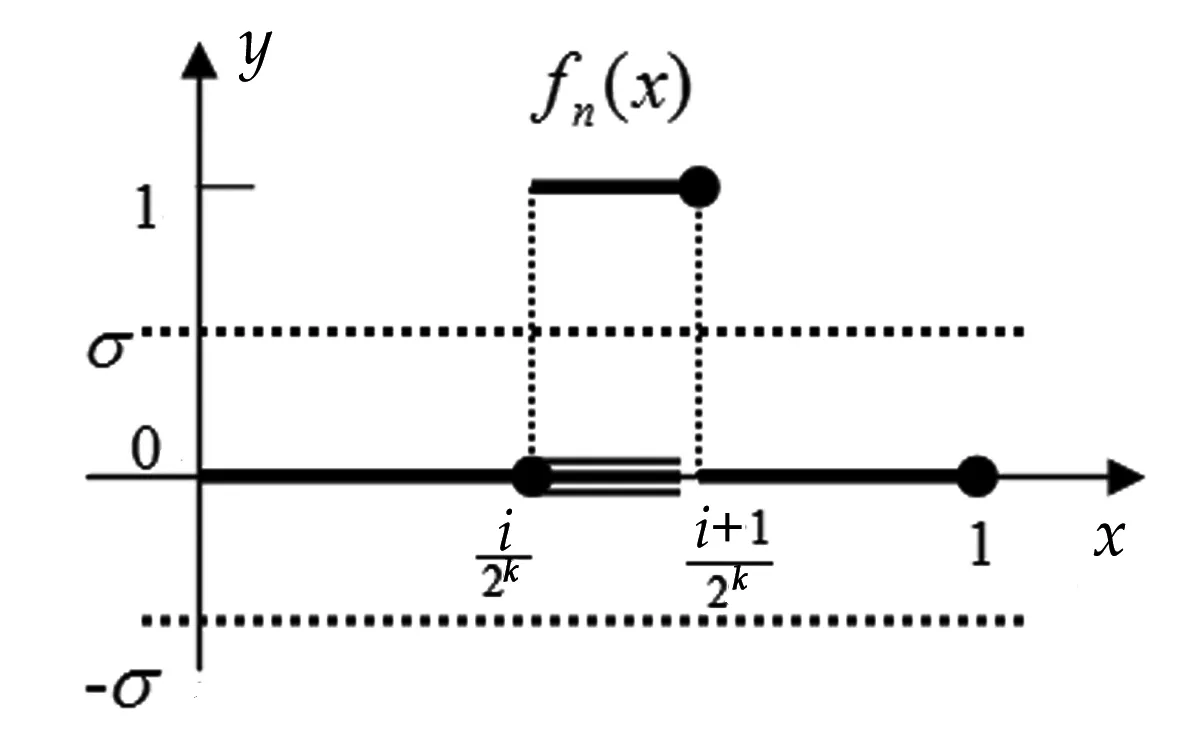
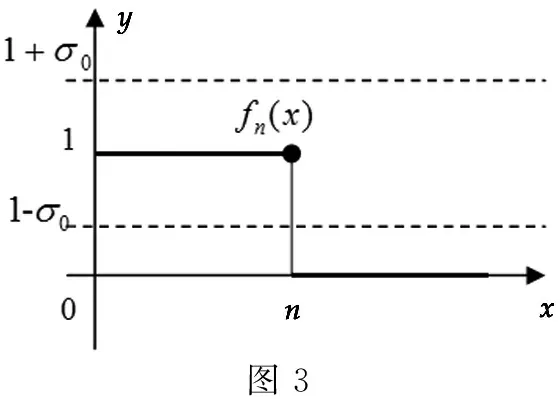
={x∈E:f(x)-σ 此时,应想到数学分析中讨论函数列收敛的带状区域: {(x,y):x∈E,f(x)-σ 这里与数学分析的区别仅在于只考虑x构成的点集。 于是定义1的几何意义为对∀σ>0,y=fn(x)的图像落在带状区域: {(x,y):x∈E,f(x)-σ 外部的那些点的横坐标x构成的点集: En=E[|fn-f|≥σ] 当n→∞时,m(En)→0。注意这里点集En的位置可在E内改变。于是,依测度收敛不考虑En位置的改变,只要其测度m(En)→0。如图1所示。 由此可知,依测度收敛取决于函数列在整个定义域的性态,而不是每个点的性态。 通过几何意义形象地理解依测度收敛,便可容易地判断下面一些函数列的依测度收敛性。 图1 首先,回到例1中的函数列: 事实上,对∀σ>0,不妨设0<σ<1,由下面的函数图像(图2)可见y=fn(x)的图像落在带状区域: {(x,y):x∈[0,1],-σ 外部的那些点的横坐标x构成的点集: 图2 利用此几何意义,还可看到一些函数列的不依测度收敛,如下面的例2。 例2 设E=[0,+∞),函数列: fn(x)=χ(0,n](x),x∈E,n=1,2,…, {(x,y):x∈E,1-σ0 外部的那些点的横坐标x构成的点集: En=E[|fn-1|≥σ0]=(n.TIF,+∞), 由以上的分析可见,借助函数图像和点集特征得到的依测度收敛的几何意义,就可形象地理解这一抽象的概念。 按定义来讨论依测度收敛的性质是可能的选择之一,但数学中的一般经验是过分依赖于定义必行之不远。不过,学生已熟知数学分析中函数列收敛的一些性质,如若fn→f,gn→g,则fngn→fg;又若fn→f,g连续,则g°fn→g°f等。于是,可将依测度收敛转化为普通收敛来讨论其性质,而不是通过用测度论的定义的方法来论证。若要实现依测度收敛到普通收敛的转化,需要借助下面的Riesz定理。 此定理说明了“依测度收敛函数列包含a.e.收敛子列”。这时,可借助普通收敛函数列的性质来导出依测度收敛函数列的性质。以下举例说明这种转化法在推导依测度收敛性质中的应用。 假定下面所涉及的函数都是点集E上的可测函数。 例3(唯一性) 若fn⟹f,fn⟹g,则f=g,a.e. 例4 设m(E)<∞,若fn⟹f,g∈C(R),则g°fn⟹g°f。 证明(反证) 若结论不成立,即: ∃ε>0,σ>0,对∀k≥1,∃nk≥k,使得: mE[|g°fnk-g°f|≥σ]≥ε (*) 这种方法主要依赖于依测度收敛与a.e.收敛的相互转换以及通常收敛性的熟知性质,而没有用精细的测度论方法推导,从而使证法简捷。但是,这种转化法不能解决需要用精细的测度论证的一些问题。 为了使依测度收敛的概念易于理解,通过以上探讨,可先构造处处不收敛的特殊函数列,引出依测度收敛的定义,再运用函数图像和点集的特征给出依测度收敛的几何意义,便可以形象地理解这一抽象概念。最后,借助依测度收敛与几乎处处收敛的相互转换,便可以简捷地论证依测度收敛的一些性质。在依测度收敛概念的教学中合理地运用构造法、形象法及转化法可使这一概念形象具体。近几年,笔者采用以上方法讲授依测度收敛的概念,效果很好。学生可形象且深刻地理解这种收敛性,同时能够快速地判断一些函数列是否依测度收敛以及用依测度收敛的性质解决一些问题。由此可见,如果在实变函数课程的教学中,经常运用函数图像的方法将抽象概念形象化,学生将改变对实变函数抽象、难于理解的看法。 [1]程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].北京:高等教育出版社,2010:89-91 [2]邓东皋,常心怡.实变函数简明教程[M].北京:高等教育出版社,2005:69-70 [3]唐秀娟.类比建构在实变函数教学中的应用[J].高师理科学刊,2004,24(4):10-13 [4]邓东皋,常心怡.为什么要学习勒贝格积分[J].高等数学研究,2006,9(4):4-10 [5]汪威,王增辉,李健.形象思维在实变函数教学中的应用[J].新乡学院学报:自然科学版,2012,29(5):469-470 [6]杜波.构造性方法在实变函数教学中的应用[J].高等数学研究,2012,15(4):89-90 (责任编辑:汪材印) 10.3969/j.issn.1673-2006.2015.02.032 2014-09-30 国家级特色专业“数学与应用数学”建设项目(TS11496)。 崔颖(1983-),女,安徽固镇人,硕士,讲师,主要研究方向:泛函数分析。 O174.1 A 1673-2006(2015)02-0122-03

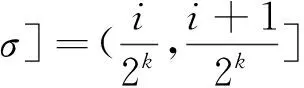
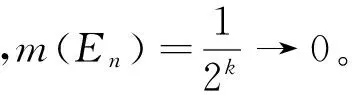
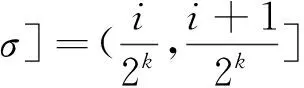
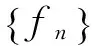
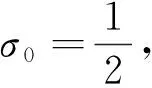

3 转化法推导性质



4 结束语

