(2+1)维Lax-Kadomtsev-Patviashvili方程的Painlevé分析和精确解

王竟博， 胡恒春

(上海理工大学理学院，上海 200093)

(2+1)维Lax-Kadomtsev-Patviashvili方程的Painlevé分析和精确解

王竟博， 胡恒春

(上海理工大学理学院，上海 200093)

由Weiss，Tabor和Carnevale(WTC)提出的Painlevé分析法是目前最有效且应用广泛的直接判别非线性偏微分方程的方法之一.借助符号计算软件Maple，首先将判断非线性系统可积性的WTC方法应用于(2+1)维Lax-Kadomtsev-Patviashvili(Lax-KP)方程中，通过领头项分析得到两种情况.然后分别寻找共振点，并验证共振条件是否成立，判别了(2+1)维Lax-KP方程具有Painlevé不可积性.应用Painlevé标准截断展开和非标准截断展开两种方法，构造了Lax-KP方程不同形式的精确解，通过适当选取常数值发现这些精确解都是扭结形状的孤波解.

Lax-KP方程；Painlevé可积性；精确解；WTC方法

由于孤立子在物理学及其它许多学科得到了广泛应用，引起了许多物理学家对寻找具有孤立子解的完全可积模型研究的极大兴趣.其中，最有影响的可积模型有Kd V方程、MKd V方程、Burgers方程、Sine-Gordon方程、非线性薛定谔方程等.关于非线性系统的可积性以及求解问题，已经建立和发展了许多有效的方法，如反散射变换方法、达布变换法、双线性及多线性方法、经典和非经典李群法等.其中，1983年由Weiss，Tabor和Carnevale发展的Painlevé分析法已被公认为是最成功、且应用最广泛的方法之一，通常被称为WTC方法[1].把WTC方法应用于非线性偏微分方程中，不仅可以得到可积模型的Painlevé性质、Lax对、Backlund变换、双线性形式等性质，还可以得到许多可积模型的精确解[2-5].1984年，Kruskal等对WTC方法进行了简化，将奇异流形上的函数假设为其中一个变量的线性关系，大大简化了计算的复杂性.但传统的WTC方法也有局限性，对于没有Painlevé性质的方程，一般不能得到更为丰富的孤子解.后来，Conte[6]，Pickering[7]以及Lou[8]先后通过不同途径推广了WTC方法，得到了更多、更简洁的非线性偏微分方程的新精确解.

1 Lax-KP方程简介

Lax[9]通过推广Kd V方程的双线性形式，获得了著名的五阶Lax非线性方程.Kadomtsev和Petviashvili通过延长Lax方程，得到新的完全可积的Lax-Kadomtsev-Petviashvili(Lax-KP)方程[10]

Wazwaz[11]利用tanh-coth方法求出了式(2)的单孤子解和三角函数解，用Hirota双线性方法和Hereman的简化形式求出了该式的多孤立子解.于金倩等[12]用李群方法得到了式(2)的对称、群不变解以及若干相似约化方程.判别其它的高维或低维非线性系统的Painlevé可积性及其新精确解，很多作者已经取得了一定的研究成果[13-14].还有一些学者借助于其它求解非线性系统的方法，如指数函数展开法、达布变换法等，研究了耦合非线性系统的复子解和周期解[15-17].本文将借助判断非线性系统可积性的WTC方法来研究(2+1)维Lax-KP方程是否具有Painlevé可积性，并进一步利用标准截断展开和非标准截断展开两种方法构造Lax-KP方程的新精确解.

2 Lax-KP方程Painlevé不可积性

首先，令任意的奇异流形φ(x，y，t)=0，势函数u=u(x，y，t)的洛朗展开式为

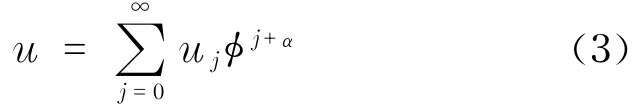
然后，令u～u0φα，则由领头项分析可得到如下两种情况:

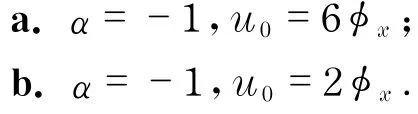
要检验式(2)是否具有Painlevé性质，按照Painlevé可积性的步骤，需找出式(2)所有的共振项，并验证所有共振项是否满足相容性条件.下面给出这两种情况的具体分析过程.

步骤1采用找对称方程的方法求解共振项，令

把式(4)代入式(2)后，得到有关函数uj的递推关系式

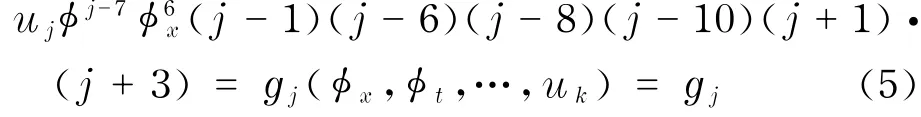
式中，gj是仅仅依赖于uk(k=0，1，2，…，j-1)和φ导数的复杂函数.由式(5)可以看出，所求的共振项为j=-3，-1，1，6，8，10.在j=-1的共振点对应于展开函数的任意性；j=-3不符合共振项的定义，故舍去.

步骤2检验j=1，6，8，10时，是否满足相容性条件.

为方便起见，采用Kruskal的简化方法，取

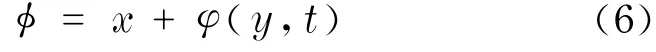
式中，φ=φ(y，t)是自变量为y和t的函数.

由于共振项最大正整数是10，所以有限截断展开式为

将式(6)和式(7)代入式(2)，依次比较φ的各幂次系数，可得到一系列等式可见，u10不是任意函数，所以此时Lax-KP方程不具有Painlevé可积性质.

b.当α=-1，u0=2φx时.

步骤1采用找对称方程的方法求解共振项，同样令

把式(6)代入式(2)中，得到有关函数uj的递推关系式

式中，fj是仅仅依赖于uk(k=0，1，2，…，j-1)和φ导数的复杂函数.由式(8)可以看出，共振项为j= -1，1，2，5，6，8.在j=-1的共振点对应于展开函数的任意性.

步骤2检验j=1，2，5，6，8时，是否满足相容性条件.

可见，u8不是任意函数，所以Lax-KP方程也不具有Painlevé可积性质.综合上述两种情况可知，Lax-KP方程并不具有Painlevé可积性质.

3 Lax-KP方程的精确解

尽管Lax-KP方程不具有Painlevé可积性质，仍可以利用Painlevé截断展开方法来构造其精确解.下面利用Conte展开法来构造Lax-KP方程的精确解.Conte展开法具有如下形式

式中，ξ是与x，y和t的任意函数，且满足

显然，当N=2时，式(9)和式(10)为Pickering提出的不变形式展开.在此基础上，不失一般性，取N= 2，令

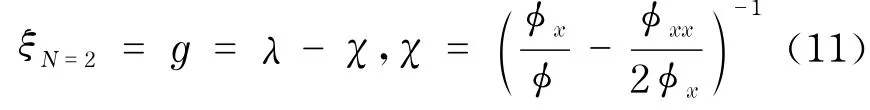
式中，λ是任意常数；φ是任意奇异流形.当λ=0时，式(9)中的函数被χ所替换后得到的新展开式恰好是常说的Conte展开式.由式(11)可知S，C和K是Möbius变换下的不变量.经计算可验证相容性条件gtx=gxt，gty=gyt，gxy=gyx成立.

当式(9)中的函数被g所替换后，所对应的标准截断展开式

把标准截断展开式代入Lax-KP方程并消去所有各阶g的系数，可以得到一系列复杂的由函数u0，u1，u2，S，C和K组成的表达式.此时，要想得到Lax-KP方程的精确解是很困难的.但为了得到相对简单的孤子解，就可以把它们选择成常数(可用相对应的小写字母表示)，将会得到一组非平凡解

式中，c1为积分常数.

当式(19)中的函数被g所替换后，所对应的非标准展开式

同样，把非标准截断展开式代入Lax-KP方程并消去所有各阶g的系数，也可以得到一系列复杂的由函数u0，u1，u2，S，C和K定义的表达式.与标准截断方法类似，可求出另一组非平凡解

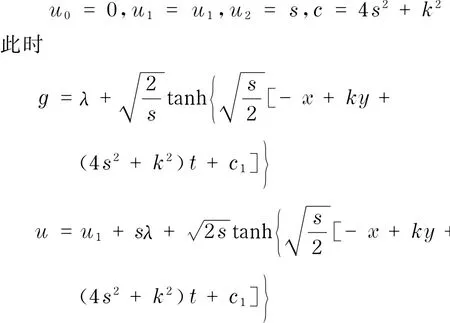
适当地选取不同常数值，可发现通过标准截断和非标准截断这两种方法得到的Lax-KP方程的精确解都是扭结形状的孤立波解.

4 结 论

利用判别非线性系统可积性的WTC方法检验了(2+1)维Lax-KP方程的Painlevé不可积性，并通过Painlevé标准截断展开和非标准截断展开两种方法构造了Lax-KP方程的新精确解.对于(2+ 1)维Lax-KP方程的其它可积性质和新形式的精确解，如达布变换、CK直接法约化方法、分离变量解等，将是今后工作的研究重点.

[1] Weiss J，Tabor M，Carnevale G.The Painlevéproperty for partial differential equations[J].Journal of Mathematical Physics，1983，24(3):522-527.

[2] Lin J.Dromion and multi-soliton structures of the (2+1)dimensional higher-order Broer-Kaup system [J].Chinese Physics Letters，2002，19(6):765-768.

[3] Lin J，Li H M.Painleve integrability and abundant localized structures of(2+1)-dimensional higher order Broer-Kaup system[J].Zeitschrift für Naturforschung A，2002，57(12):929-936.

[4] Lou S Y，Wu Q X.Painlevéintegrability of two sets of nonlinear evolution equations with nonlinear dispersions[J].Physics Letters A，1999，262(4/5): 344-349.

[5] Lou S Y，Chen C L，Tang X Y.(2+1)-dimensional (M+N)component AKNS system:Painlevé integrability，infinitely many symmetries，similarity reductions and exact solutions[J].Journal of Mathematical Physics，2002，43(8):4078-4109.

[6] Conte R.Invariant Painlevéanalysis of partial differential equations[J].Physics Letters A，1989，140 (7/8):383-390.

[7] Pickering A.A new truncation in Painlevéanalysis [J].Journal of Physics A:Mathematical and General，1993，26(17):4395-4405.

[8] Lou S Y.Extended Painlevéexpansion，nonstandard truncation and special reductions of nonlinear evolution equations[J].Zeitschrift für Naturforschung A，1998，53(8):251-258.

[9] Lax P D.Integrals of nonlinear equations of evolution and solitary waves[J].Communications on Pure and Applied Mathematics，1968，21(5):467-490.

[10] Kadomtsev B B，Petviashvili V I.On the stability of solitary waves in weakly dispersive media[J].Soviet Physics Doklady，1970，15(6):539-541.

[11] Wazwaz A M.Multiple-soliton solutions for the Lax-Kadomtsev-Petviashvili(Lax-KP)equation[J]. Applied Mathematics and Computation，2008，201(1/ 2):168-174.

[12] 于金倩，王婷婷.(2+1)维Lax-Kadomtsev-Petviashvili (Lax-KP)方程的对称和精确解[J].聊城大学学报(自然科学版)，2009，22(3):14-18.

[13] Xu G Q.Painlevéintegrability of a generalized fifthorder KdV equation with variable coefficients:exact solutions and their interactions[J].Chinese Physics B，2013，22(5):050203.

[14] Zhi H Y，Chang H.Invariance of Painlevéproperty for 665-673.some reduced(1+1)-dimensional equations[J]. Chinese Physics B，2013，22(11):110203.

[15] 胡恒春，王丽金，刘磊.KdV-Burgers-Kuramoto方程另一类指数函数求法及新的精确解[J].上海理工大学学报，2013，35(2):131-134.

[16] 张玲，桑本文，胡恒春.耦合mKdV系统的非奇异正子解、负子解及复子解[J].上海理工大学学报，2012，34 (1):76-80.

[17] 斐胜兵，张卫国，李想.色散项数为负的MKdVBrugers方程的有界行波解[J].上海理工大学学报，2014，36(3):205-216.

(编辑:董 伟)

PainlevéAnalysis and Exact Solutions of the(2+1)-Dimensional Lax-Kadomtsev-Patviashvili Equation

WANG Jingbo， HU Hengchun
(College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China)

The Painlevéanalysis method developed by Weiss，Tabor and Carnevale is one of the most effective and extensively used methods to test the integrability of the nonlinear partial differential equation.With the help of symbolic computation system Maple，the(2+1)-dimensional Lax-Kadomtsev-Patviashvili(Lax-KP)equation was proved to be Painlevénon-integrable by using the Weiss，Tabor and Carnelvale(WTC)method.The leading order analysis helps one to find two cases and verify that the recursion relations are established directly.New exact solutions of the (2+1)-dimensional Lax-KP equation were obtained by the standard and nonstandard truncation expansions respectively，and all the solutions are both kink solitary solutions when selecting proper constants.

Lax-KP equation；Painlevéanalysis；exact solutions；WTC method

O 13

A

1007-6735(2015)02-0126-04

10.13255/j.cnki.ju sst.2015.02.005

2013-11-11

国家自然科学基金资助项目(11071164，11201302)；上海市自然科学基金资助项目(10ZR1420800)；上海市重点学科建设资助项目(XTKX2012)

王竟博(1990-)，女，硕士研究生.研究方向:孤立子与可积系统.E-mail:wangjingbo26@163.com

胡恒春(1976-)，女，副教授.研究方向:孤立子与可积系统.E-mail:hhengchun@163.com

��编号:1007-6735(2015)02-0130-06 DOI:10.13255/j.cnki.ju sst.2015.02.006