管内振动壁面射流流场的数值模拟
朱志文, 王宏光
(上海理工大学能源与动力工程学院,上海200093)
管内振动壁面射流流场的数值模拟
朱志文, 王宏光
(上海理工大学能源与动力工程学院,上海200093)
采用动网格技术和k-ε两方程湍流模型,通过求解二维非定常不可压雷诺时均Navier-Stokes方程,对局部壁面振动的管内射流流场进行数值模拟,分析局部振动壁面的振幅和频率对流动的影响.结果表明,射流孔下游壁面静压随振幅、频率的增加而增加;射流孔附近静压在126°相位角降到最低.射流孔的平均流量随振幅的增加而减小,随频率的增加而增加;流量波动随振幅、频率的增加而增大,高频率对主流的影响更加明显.
管内流动;射流;振动壁面;气膜冷却
随着燃气轮机的发展,燃气温度的提高使得叶片冷却技术成为关键技术之一[1-3].实际工作中的涡轮动叶片是刚性很大的弹性体,由于高速旋转,并受到静叶尾迹、转子不平衡等因素的激励,涡轮动叶片处于小幅高频的振动状态[4].振动作为强化传热的手段之一,在传热学领域受到重视.振动强化传热分为两类[5]:第一类为传热面振动;第二类为流体振动(脉动).在涡轮动叶栅中,两类振动强化传热现象
都存在,而且第二类振动强化传热对叶片冷却效果影响的研究较多[6].例如,分析静叶栅尾迹形成的不稳定尾流、来流湍流度等流动不稳定因素对动叶片传热和气膜冷却效果的影响;在叶片内部冷却通道设置扰流肋片或扰流柱,对流体进行扰动,造成流动不稳定,从而实现强化传热.但到目前为止,对第一类振动强化换热问题,即涡轮动叶片振动与叶片冷却效果关系的研究还未见报道.
振动会对振动体表面流体产生直接作用力[7-10],即振动体表面与流体有动量和能量的交换,造成流体的扰动,影响流体与振动体表面的传热效果.因此,认识和掌握振动表面的流动和传热规律,对分析涡轮动叶片的热负荷与可靠性具有重要意义.
本文将振动叶片气膜冷却孔附近的流动问题简化为壁面局部振动的二维管内射流模型,研究射流孔附近的壁面局部振动对流动状态的影响.
1 计算模型
计算模型如图1所示,流动区域的长高比为5∶1,振动区域FG位于BD的中心,长度为1.射流孔E位于FG的中心,宽度为0.1,射流管长为0.3.射流孔随振动区域FG振动.

图1 简化模型图Fig.1 Simplified model diagram
以水为工质,进口边界AB采用速度入口,给定进口流速v0=20 m/s,湍动能和湍动耗散率由经验公式计算得出.射流孔E采用压力入口,给定总压P0=199 640 Pa.下壁面BFGD和上壁面AC给定无滑移条件.出口边界CD给定静压P1= 101 325 Pa.
采用Fluent软件,离散格式选择二阶迎风格式,湍流模型选择Realizable k-ε,第一层网格距离边界0.000 2 m,网格总数为52万,时间步长取0.000 5 s,隐式时间格式.压力与速度的耦合采用PISO方法.图2为射流孔附近的网格,靠近壁面采用结构化网格,其余位置采用非结构化网格.

图2 射流孔附近的网格Fig.2 Mesh at jet hole
2 计算结果
2.1 壁面不振动时射流流场计算
壁面在不振动(稳态)的情况下,计算管内的流动状态.建立xoy坐标系,坐标原点为B点,x轴与BD重合,向右为正方向.在射流孔下游定义线段MN,距离壁面为y=0.03,x坐标在2.55~3.50之间.壁面不振动时线段MN上的静压P分布如图3所示.f为振动频率,h为振幅,α为相位角.

图3 线段MN在不同频率下的静压分布Fig.3 Static pressure distribution on line MN at different frequency
2.2 壁面振动时射流流场计算
壁面局部振动区域FG作简谐振动,振动初始位置壁面与x轴重合,此时相位角为0°.壁面从初始位置向y轴正方向运动.振动与非振动区域的连接点F和G保持不动,保证了振动边与非振动边的连接.振动区域FG的位移和速度边界条件采用UDF控制,现给定其位移规律

式中,T为振动周期;L为点F和点G间的距离;xF为F点的x坐标.
振动频率和振幅如表1所示(见下页),计算6个算例,比较振幅、频率和相位角对流动的影响.

表1 振动区域FG的振动边界条件Tab.1 Vibration boundary conditions of the vibration area FG
计算过程中检测出口边界上点H(5,0.08)的总压P4随时间t的变化情况,如图4所示,可以看出,3个周期后该点总压基本呈周期性变化,故认为3个周期后的数据基本稳定.现选择第5周期的数据进行比较分析.

图4 出口点H的总压变化Fig.4 Total pressure change at point H
2.2.1 频率对静压的影响
图3是在FG振幅为0.002 m,相位角为0°,频率为100,200,300,400 Hz时线段MN上的静压分布对比图,可以看出,随着频率的增加,静压迅速增加,振动壁面向流体输送了能量.图5是静压提取点(J0,J1,J2,J3,J4,J5)在模型中的位置.图6是0°相位角下图5中不同点的静压随斯特劳哈尔数Sr的变化.各点的静压随着Sr的增加而增加,不同位置点的静压增加趋势不同.
2.2.2 振幅对静压的影响
给定FG振动频率为100 Hz,相位角为0°,振幅为0.001,0.002,0.003 m时线段MN上的静压分布如图7所示,可以看出,振幅越高,线段MN上的静压波动幅度越大.从图7可以看出,由于振动频率相同,不同振幅下静压分布的形态接近.
2.2.3 相位对静压的影响

图5 静压提取点在模型中的位置Fig.5 Location of static pressure extraction point in the model
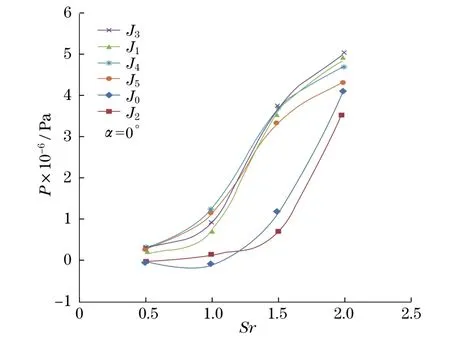
图6 不同点的静压随Sr的变化Fig.6 Static pressure change with different Sr at different points

图7 线段MN在不同振幅下的静压分布Fig.7 Static pressure distribution on line MN at different amplitude
图8是FG振动频率为100 Hz,振幅为0.002 m,不同振动相位角时,线段MN上的静压分布图,可以看出,静压分布随壁面振动的相位角变化,在126°附近降到最低.
2.2.4 速度云图对比
图9是壁面不振动时,算例Ⅰ,Ⅳ,Ⅵ在相位角为0°时的速度云图对比.对比图9(b)和图9(c)可以看出,不同振幅下的速度云图形态基本相同.对比图9(b)和图9(d)可以看出,不同频率下的速度云图有明显差别,高频率对主流影响更加明显.

图8 线段MN在不同相位角下的静压分布Fig.8 Static pressure distribution on line MN under different phase angle
2.2.5 射流流量对比
各算例在1个振动周期内的平均流量Q对比如表2所示,可以看出,壁面振动时射流孔的平均流量大于不振动时的.振幅对射流平均流量的影响如图10所示,随着振幅的增加,平均流量减小.频率对射流平均流量的影响如图11所示(见下页),随着频率的增加,平均流量增大.
各算例流量随相位角的变化如图12所示(见下页).在0~90°之间某些工况存在流量小于稳态流量的情况,可以得出,随着振幅的增加,流量在1个周期内的波动增大.随着频率的增加,流量的波动也增大.图13(见下页)是算例Ⅰ振动边界位移L、射流流量Q和流场中点J0(2.65,0.03)的静压P在1个周期内的相位角对比,可以看出流量和静压相对边界振动的滞后情况.

图9 速度云图(α=0°)Fig.9 Contour of velocity(α=0°)

表2 不同算例下通过射流孔E的平均流量Tab.2 Average flow rate through jet E hole in different examples

图10 振幅对平均流量的影响Fig.10 Influence of amplitude on average flow rate

图11 频率对平均流量的影响Fig.11 Influence of frequency on average flow rate

图12 流量随相位角的变化Fig.12 Flow rate change with phase angle

图13 算例Ⅰ综合对比Fig.13 Comprehensive comparison in exampleⅠ
3 结 论
a.射流孔下游壁面附近的静压随振幅、频率的增加而增加,随无量纲参数Sr的增加而增加;不同振幅下的速度分布基本相同.射流孔附近静压在126°相位角时降到最低.
b.振动状态的射流平均流量高于静止状态.平均流量随振幅的增加而减小,随频率的增加而增大.流量的波动随振幅、频率的增加而增大.
[1] Gräf L,Kleiser L.Film cooling using antikidney vortex pairs:effect of blowing conditions and yaw angle on cooling and losses[J].Journal of Turbomachinery,2013,135(1):011008.
[2] Fujimoto S,Okita Y,Fukuyama Y,et al.Study on advanced internal cooling technologies for the development of nextgeneration small-class aircraftengines[J].Journal of Turbomachinery,2010,132(3):031019.
[3] 艾书民,王克明,缪辉,等.稳态温度场作用下涡轮叶片振动特性的研究[J].沈阳航空航天大学学报,2011,28(4):17-21.
[4] 王一平,卢艳华,朱丽,等.振动平板的传热性能实验[J].天津大学学报,2010,43(6):549-552.
[5] 林宗虎.强化传热及其工程应用[M].北京:机械工业出版社,1987.
[6] 韩介勤,桑地普·杜达,斯瑞纳斯·艾卡德.燃气轮机传热和冷却技术[M].程代京,谢永慧,译.西安:西安交通大学出版社,2005.
[7] 裘进浩,李大伟,聂瑞,等.增加翼型升力的局部振动流动控制技术[J].南京航空航天大学学报,2012,44 (5):638-644.
[8] 曹卫东,张晓娣,高一.逆压梯度边界层壁面局部微振动诱导大涡结构[J].江苏大学学报(自然科学版),2011,32(5):522-527.
[9] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.
[10] 宿艳彩,葛培琪,闫柯,等.流体绕流不同方向振动圆柱换热特性数值分析[J].振动与冲击,2011,30(10): 221-223.
(编辑:石 瑛)
Numerical Simulation of Jet Flow on Vibration Wall in Tube
ZHU Zhiwen, WANG Hongguang
(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
The jet flow on vibration wall in tube was simulated based on solving the twodimensional incomperssible Reynolds averaged Navier-Stokes equation with moving grid and k-ε two-equation turbulence model.The influences of amplitude and frequency of wall vibration on the flow were discussed.The results show that the static pressure on the wall at the jet hole downstream increases with the increase of the amplitude and frequency.The static pressure reaches the lowest under the phase angle of 126°.The average flow rate of the jet flow decreases with the increase of the amplitude,but increases with the increase of the frequency,and the flow rate fluctuation increases with the increase of the amplitude and the frequency.High frequency has more obvious effects on the mainstream.
flow in tube;jet flow;vibration wall;film cooling
TK 14
A
1007-6735(2015)02-0110-05
10.13255/j.cnki.ju sst.2015.02.002
2014-01-05
高等学校博士学科点专项科研基金联合资助项目(20123120110009)
朱志文(1991-),男,硕士研究生.研究方向:叶轮机械气动热力学.E-mail:zhuzhiwen0104@126.com通信作者:王宏光(1962-),男,教授.研究方向:叶轮机械气动热力学.E-mail:whg2005@usst.edu.cn
��编号:1007-6735(2015)02-0115-07 DOI:10.13255/j.cnki.ju sst.2015.02.003

