用空间向量法解决球的问题

黑龙江省鹤岗市第一中学 舒敬宇 高 昕

有关球的问题在历年的高考中既是热点，又是难点。从近几年新课标高考的试题来看，对本部分知识的考查多为一道小题，注重考查学生的空间想象能力和逻辑思维能力。将空间向量法引入到立体几何中，将其转化为代数中解方程的问题，从而得到了解决此类问题的又一方法。

【例题】已知某个几何体的三视图如下图所示，根据图中标出的尺寸（单位：cm），如果这个几何体内接于一个球O1，那么这个球O1的半径是____________cm。

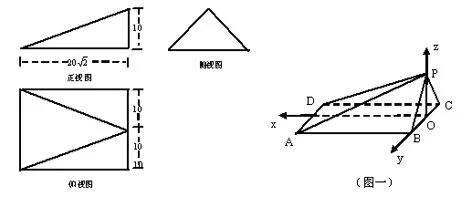
【试题分析】本题是研究几何体外接球问题，借助空间向量法，建立空间直角坐标系，根据球心到该几何体每一个顶点的距离都相等，列方程，解方程，将立体几何问题转化为代数的问题。

解：根据三视图还原出该几何体的直观图，如（图一）取BC的中点O为坐标原点,建立空间直角坐标系O-xyz，则

设球心O1(x,y,z)，球的半径为R，则

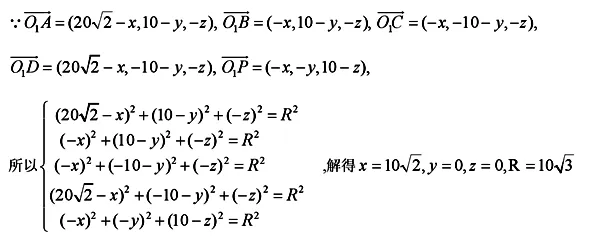
【变式】将例题中的如果这个几何体内接于一个球O1，变为这个几何体内切球为球O2，那么这个球O2的半径是___________cm。

【试题分析】本题是研究几何体内切球问题，借助空间向量法，建立空间直角坐标系，根据球心到该几何体每一个面的距离都相等，将立体几何问题转化为解方程的问题。

解：根据三视图还原出该几何体的直观图，如（图一）取BC的中点O为坐标原点,建立空间直角坐标系O-xyz，则

设球心O2(x,y,z)，球的半径为r，球心O2到平面ABP的距离为d1，到平面BCP的距离为d2，到平面CDP的距离为d3，到平面ADP的距离为d4，到底面ABCD的距离为d5，则d1=d2=d3=d4=d5=r。

设平面ABP的法向量

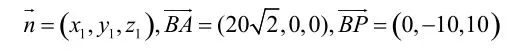
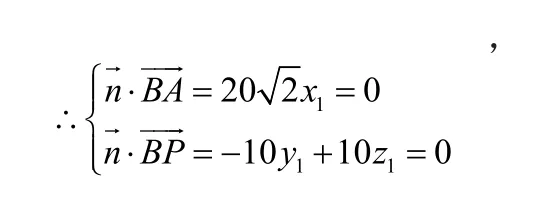
令y1=1，则z1=1,x1=0，

所以

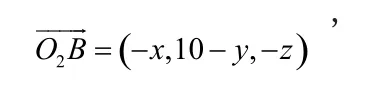
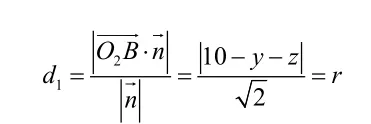
同理可得

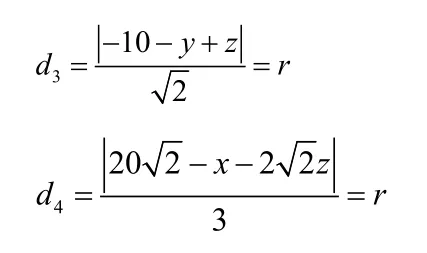
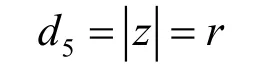
解得