一种长基线高精度时差测向算法

郁 涛

（中国电子科技集团公司第五十一研究所，上海 201802）

一种长基线高精度时差测向算法

郁 涛

（中国电子科技集团公司第五十一研究所，上海 201802）

由一维双基程差方程即能直接获得长基线测向公式，在进行合理简化之后又可得到形式非常简单的单基程差测向式。如仅从外在表现形式而言，和现有的短基线近似测向式相比，新的在较长基线上仍具有较好计算准确度的单基线测向式，仅是将计算基准点从基线的端点移到了基线的中点位置处。初步的误差分析表明，在基线大于数千米的条件下，基于时差测量的测向误差可小于0.1°。

时差测向；超精度；长基线；无源定位

0 引言

时差测向以其原理简单、测向精度高而早被提出，原理上时差信息直接表示了来波的方位信息，故无须对输入信号做解调处理，最适合脉冲制信号环境。此外，时差测量还具有所需的信道数量少、对天线方向图的要求不苛刻、测向精度与频率测量无关等特点。

作为无源探测军事应用的一种高精度测向手段，时差测向技术的研究在近40年里取得了重大突破，但迄今为止的相关研究主要聚焦在短基线时差测向方法上［1－5］，这一方面是战术需要，另一方面则涉及数学模型，现有的基于短基线的测向公式仅是一种非常近似的计算方法，如将其延伸到长基线测量，则会出现计算准确度变劣而无法应用的状况。

基于测向精度与基线长度成正比的原理，如能在数学上给出适用于长基线时差测向的模型，则理应就能得到超精度的测向性能。但仅利用时差方程本身进行求解是难以得到线性的定位解析结果的［6－10］。最近的分析结果是如能将程差和几何关系结合起来，则即能得到形式简单的一维双基定位方程的线性解［11，12］，由此即能得到适用于长基线的时差测向公式。但基于一维双基方程的求解方式将涉及三站布阵，这事实上是不利于工程应用的，不仅增加了设计成本，而且布阵中的各种误差因素也随之增加，因为对于长基线而言，三站难以位于一条直线上，这样就需要考虑非直线阵的测向方程，由此就会产生基线间夹角的测量误差，根据现有的某些分析经验，夹角的测量误差对定位精度的影响还是比较大的［13］。因此，双站测向的方式是最为有利的方式。基于这样的需求，本文在描述多站长基线时差测向方法的基础上，通过适当的简化处理，给出了一种双站单基时差测向方法。

1 程差测向

1.1 双基测向式

一维双基阵列示意图如图1所示。

图1 一维双基阵列

对于图1所示的几何模型，设程差为：

另由余弦定理可列出如下几何方程：

因有x=r2sinθ，故几何辅助方程可改写为：

将程差式代入几何辅助式（1）和式（2），在移项整理后有如下的二元一次线性方程组：

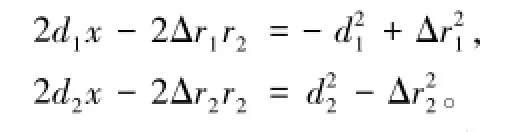
从中可以直接解出基于程差测量的目标到达角［14］：

1.2 单基测向式

如两基线相等，有

根据现有的研究结果［15］，可做近似处理：Δr1≈Δr2，据此对测向式进行简化后有：

所以，

由此就能得到如下的结论：如采用单基线测向，则正确的测向参考基准点是在单基线的中点位置处，而不是在单基线的左右端点处。

1.3 基于基线中点测向解的准确度

基于严格数学关系所导出的双基测向式对于任意长度的基线应用都是准确的。本节验证由近似简化所得到的单基测向式（3）的准确性。

模拟计算结果表明，单基测向式（3）不仅对短基线是正确的，而且还可应用于较长基线，当目标距离为300 km、基线长度小于20 km时，测向式的相对计算误差曲线如图2所示。

图2 单基测向式的相对计算误差

模拟计算表明，对于300 km远的目标，当基线长度大于50 km时，相对计算误差将超过1.5%；当基线长度大于100 km时，相对计算误差将超过5%。此外，相对计算误差与目标径向距离成反比，因此，在采用相同基线长度的情况下，对于较近的目标，相对计算误差会逐渐变劣。

2 时差测向精度分析与对比

2.1 双基测向精度

式中，

忽略站间基线长度测量误差，仅由时差测量误差所产生的测向误差为：

式中，σΔt为时差测量的均方根误差。

当目标距离为300 km、不同的基线长度时的测向误差曲线如图3所示，模拟计算时取时差测量误差均方根值σΔt=50 ns。

图3 三站双基时差测向误差

2.2 单基测向精度

基于上述研究结果，可立即得到长基线双站时差测向公式：

式中，c为光速；Δt为时差。

对测向式进行微分后可得到：

由此得到测向误差：

式中，σt为时差测量误差均方根值。

当目标距离为300 km、基线长度为3 km、不同时差测量误差均方根值时的测向误差曲线如图4所示。从图4中可以看到，如时差测量误差均方根值小于10 ns，则测向误差可小于0.05°。

图4 双站单基时差测向误差

3 结束语

如仅从数学分析出发，则双基、乃至多基线的基于长基线的时差测向亦应能获得好的测向精度，但已有的分析［14］和本文数值计算都表明，采用双基阵列的数学模型所得到的测向精度反而比近似简化所得到的单基测向精度低。如仅从工程设计和应用的角度，则采用单基线应是更为有利的。

如仅就所得到的单基测向公式的表现形式而言，作者的分析结果似乎仅是对现有近似测向公式的测量基准点做了一个移位修正。正是通过这样的简单移位，得到了适用于长基线应用的单基测向公式。并且基于基线中点的测向解对短基线测向也是适用的。

［1］ 王 涌，叶 斌，谢春胜.新的时差测向方法［J］.电子对抗技术，1995（3）：1－7.

［2］ 龚 渝.时差测向方法［J］.电子对抗技术，1994（2）：18－23.

［3］ 邵建华.短基线时差测向精度分析［J］.航天电子对抗，1998（l）：16－18.

［4］ 邵建华.短基线时差测向技术体制及应用前景［J］.航天电子对抗，1997（4）：23－25.

［5］ 邱丙益，盛 莹，刘春茂.基于TDOA的短基线测向精度分析与仿真［J］.无线电通信技术，2013，39（1）：67－69.

［6］ 邓 勇，徐 晖，周一宇.平面三站时差定位中的模糊及无解研究［J］.系统工程与电子技术，2000，22（3）：27－29.

［7］ 陆 静，郭克成，袁翔宇，等.解析法分析三站时差定位系统的定位精度［J］.现代雷达，2004，26（12）：20－22.

［8］ 邢翠柳，陈建民.多站无源时差定位精度分析［J］.无线电工程，2012，42（2）：32－34，48.

［9］ 赵 琨，何青益.基于GDOP的三站时差定位精度分析［J］.无线电工程，2012，42（5）：15－17，33.

［10］ 张正明，杨绍全，张守宏.平面时差定位精度分析［J］.西安电子科技大学学报，2000，27（1）：13－16.

［11］ 郁 涛.基于基线相似扩展的相差定位技术［J］.中国电子科学研究院学报2012，6（6）：650－654.

［12］ 郁 涛.对相似递推程差的一种修正方法［J］.现代导航，2014，5（4）：288－292.

［13］ 郁 涛.附加几何条件所得到的平面时差定位解析方程［J］.杭州电子科技大学学报，2013，33（5）：17－20.

［14］ 郁 涛.一维双基线相位干涉测向公式的准确解［J］.天线学报，2012，1（1）：8－11.

［15］ YU Tao.Airborne Passive Location Method Based on Doppler－Phase Difference Measuring［J］.Advanced in Mathematical and Computational Methods，2013，3（2）：85－91.

An Ultra-precision Time Difference DF Algorithm Based on Long Baseline

YU Tao
（The 51th Research Institute of CETC，Shanghai 201802，China）

The long baseline DF formula is obtained through path difference equation based on onedimensional double baseline. After performing rational predigestion for the path difference equation，a single baseline DF formula can be obtained，which has better accuracy in calculation for long baseline and very simple form.As far as external format is concerned，new formula is only transferring the orientation from endpoint intomedian point of baseline as compared with existing approximate DF formula based on shortbaseline. The error analysis based on time differencemeasurement shows that the DF error of new formula can be less than 0.1 degree on condition that baseline ismore than some kilometers.

time difference DF；Ultra-precision；long baseline；passive location

TN974

A

1003－3106（2015）09－0034－03

10.3969/j.issn.1003－3106.2015.09.09

郁 涛.一种长基线高精度时差测向算法［J］.无线电工程，2015，45（9）：34－36.

郁 涛男，（1957—），硕士，高级工程师。主要研究方向：无源探测定位。

2015-04-10