关于庞卡莱映射逼近的一个反例

温泳铭,张霞娟,胡建钧,丁昌明

(1.厦门大学数学科学学院,福建厦门361005;2.浙江商业职业技术学院,浙江杭州310053)

关于庞卡莱映射逼近的一个反例

温泳铭1*,张霞娟1,胡建钧2,丁昌明1

(1.厦门大学数学科学学院,福建厦门361005;2.浙江商业职业技术学院,浙江杭州310053)

在Wiggins S.所著的书《Global Bifurcations and Chaos》的第三章中分别讨论了在双曲奇点附近庞加莱映射与其线性逼近的误差,以及它们的导数之间的误差,即其证明了.针对该本书中提出来的庞卡莱映射线性逼近理论,构造出一个反例,通过利用等价关系和不等式等一些技巧,不仅说明了书中的上述两个逼近误差是错误的,而且指出了书中用来证明该线性逼近理论的引理都是不正确的.

庞卡莱映射;线性系统逼近;不变流形

1 庞加莱映射的逼近

本文讨论欧氏空间Rn中由常微分方程定义的动力系统.设S为动力系统的一个不变集合,p为系统相空间中的一点.过p点的轨线称为同宿轨线,如果该点同时处于S的稳定和不稳定流形中.为了研究同宿轨线附近的轨线结构,常常需要在同宿轨线附近建立一个庞卡莱映射[1-2].本文的讨论集中在双曲平衡点附近系统轨线的性质.

设方程.z=F(z),z∈Rs+u,其中F:U→Rs+u,F在U上是Cr(r≥2)且U为开集,方程的不动点是z=z0,方程存在一个轨线φ(t),且解φ(t)满足有s个特征值具有负实部,u个特征值具有正实部.

为方便起见,通过坐标变换w=z¯z0将不动点变换到w=0,方程变为.w=G(w).由假设知DG(0)有s个特征值有负实部,u个特征值有正实部.由线性代数知识,我们知道存在一个线性变换使得DG(0)=,其中A是对角线元素具有负实部的s ×s若当块,B是对角线元素具有正实部的u×u若当块.再通过同样的线性变换将前面的微分方程G(w)变为在这里(ξ,η)∈Rs×Ru,F1和F2是Cr¯1的且F1,F2=O(|ξ|2+|η|2).

将上述方程线性化,则给定η=0,存在s维线性子空间Es;给定ξ=0,存在u维线性子空间Eu.由文献[3],知存在相交于原点的Cr稳定流形Ws和不稳定流形Wu分别相切于Es和Eu.在局部范围内,用及分别代表φs(ξ)和φu(η)的图像,其中为 Ns→Ru的Cr映射,φu(η)为Nu→Rs的Cr映射(Ns与Nu各自为相应空间中原点的充分小邻域).再通过以下坐标变换作为坐标系,则η)变为:

其中f1,f2=O(|ξ|2+|η|2)且有f1(0,y)=f2(x,0) =0.

设φ(t,x0,y0)=(x(t,x0,y0),y(t,x0,y0))是方

注意到构造的上述映射P0需要知道.x=Ax+ f1(x,y),.y=By+f2(x,y)的解,但是对于大多数非线性微分方程,解一般是无法求出的,所以希望用一个映射去逼近它,在文献[1]中的构造是如下进行的:

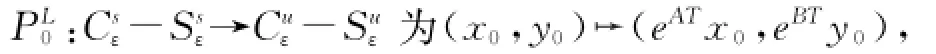
其中T满足|eBTy0|=ε.

为了更好说明此逼近映射,令x=ε¯x,y=ε¯y,其中0＜ε≪1,则式(1)变换为:

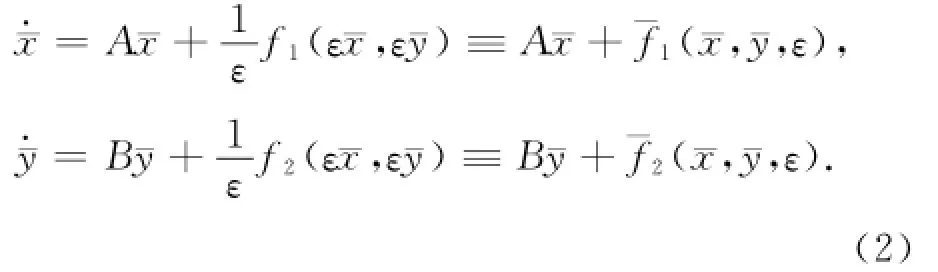
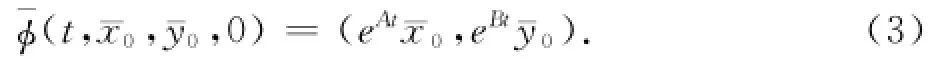
2 主要结论

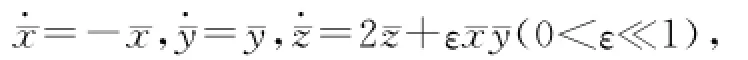
将其线性化后变为

下面说明证明这2个结论的引理3.2.3是错误的,引理证明了DεT(¯x0,y¯0,0)在Cs1¯Ss1上有界,但是根据前面得到

于是将ε=0代入得到其无界.在引理证明中证明的一个式子3.2.46b也是错误的,导致该引理错误,3.2.46b是说是有界的,我们还是用该反例来说明,首先于是Dε¯y=则Dε¯y(TL,¯x0,,这个式子用到了eTL y¯0=1,但是并不是有界的.

[1] Wiggins S.Global bifurcations and chaos[M].New York: Springer,1988.

[2] Ovsyannikov I M,Shil′nikov L P.On systems with saddle-focus homoclinic curve,math[J].USSR Sbornik, 1987,58:557-574.

[3] Hirsch M W,Pugh C C,Shub M.Invariant manifolds,lecture notes in math,v.583[M].New York: Springer,1977.

A Counterexample of the Approximate PoincaréMap

WEN Yong-ming1*,ZHANG Xia-juan1,HU Jian-jun2,DING Chang-ming1
(1.School of Mathematical Science,Xiamen University,Xiamen 361005,China; 2.Zhejiang Business College,Hangzhou 310053,China)

:Wiggins S.,in his book“Global Bifurcations and Chaos“,discussed the error between the Poincarémap and its linear approximation,and also the error between the derivations of those maps near the hyperbolic singular point in Chapter 3,respectively.In other words,he proved the conclusions:.In this paper,we present a counterexample in allusion to the linear approximation of Poincarémap in this book.Through utilizing some skills of the equivalence relation and some inequalities,not only do we illustrate the two approximation errors mentioned above are incorrect,but also the lemma,which is used to prove the theory of linear approximation,appears invalid.

Poincarémap;approximation with linear system;invariant manifold

O 175.1

A

0438-0479(2015)03-0369-03

10.6043/j.issn.0438-0479.2015.03.014

2014-04-17 录用日期:2015-01-27

*通信作者:787053198@qq.com

温泳铭,张霞娟,胡建钧,等.关于庞卡莱映射逼近的一个反例[J].厦门大学学报:自然科学版,2015,54(3):369-371.

:Wen Yongming,Zhang Xiajuan,Hu Jianjun,et al.A counterexample of the approximate Poincarémap[J].Journal of Xiamen University:Natural Science,2015,54(3):369-371.(in Chinese)